LeetCode 213. 打家劫舍 II
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
举个例子:
输入: nums = [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。视频题解
打家劫舍 II
思路来源
思路来源
知识回顾
动态规划 是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题 ,例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题,通过求解子问题的最优解推导出原问题的最优解。可以通过两点来判断一个问题能不能通过动态规划来解,一是该问题是否存在递归结构,二是对应的子问题能否记忆化。动态规划可以通过带备忘录的自上而下的递归 和自下而上的迭代 来分别实现。由于递归需要用到栈来实现,一些语言对递归的深度是有限制的,所以自下而上的迭代是动态规划的最佳实现方式。
思路解析
本题是一道经典的动态规划问题,要找到解决动态规划问题的两个突破点:推导出状态转移公式 和边界条件处理。
本题是「198.打家劫舍」的进阶版,他们之间唯一的区别是房子变成了首尾相连 ,因为第1间房和第n间房相连,我们需要考虑要不要偷第1间房。
- 如果偷
第1间房,那么第n间房一定不能偷。这个时候我们可以偷的区间就变成[0,n-1]。 - 如果不偷
第1间房,那么我们可以偷的区间就变成[1,n]。
最终就变成了求[0,n-1]和[1,n]这两个非首尾相连区间能够偷窃到的最高金额,这样就可以复用「198.打家劫舍」的思路。
首先定义dp[n]表示总共有n间房所能偷到的最高金额。
对于非首尾相连 的数组nums=[1, 2, 3, 1]其所以可能的打劫路线如下:
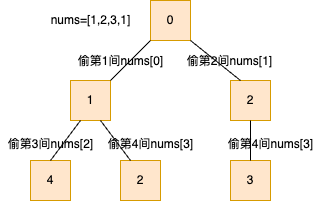
根节点到叶子节点就是一条偷盗路线,每个节点表示偷到的总金额,对于上面的例子dp[4] = 4。
状态转移公式需要分两种情况讨论:
- 偷盗路线包含
第4间房(nums[3]),根据规则这个时候第3间房(nums[2])一定是没有被偷的,那么前2间房偷到的最大金额加上第4间房偷到的金额有可能是前4间房偷的最大金额dp[4] = dp[2] + nums[3]。 - 偷盗路线不包含
第4间房(nums[3]),这个时候前3间房偷到的最大金额有可能也是前4间房偷的最大金额dp[4] = dp[3]。
上面两种情况选取最大值就可以得到4间房偷到的最大金额dp[4]=max(dp[2] + nums[3], dp[3]);
扩展到一般情况dp[n]可以分解为dp[n-1],dp[n-2]两个子问题的组合 ,得到状态转移公式:
cpp
dp[n] = max{dp[n-2] + nums[n-1], dp[n-1]}其中dp[n-2] + nums[n-1]表示偷第n间房整条路线可以偷到的最大金额。 dp[n-1]表示不偷第n间房整条路线可以偷到的最大金额。
对于边界条件 dp[0] = 0,dp[1] = nums[0],dp[2] = max{nums[0], nums[1]}。
C++ 代码
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int nums_len = nums.size();
if (nums_len == 0) return 0;
if (nums_len == 1) return nums[0];
return max(help(nums, 0, nums_len - 1), help(nums, 1, nums_len - 1));
}
int help(vector<int>& nums, int start, int len) {
if (len == 0) {
return 0;
}
if (len == 1) {
return nums[start];
}
vector<int> dp(len + 1, 0);
//边界条件
dp[1] = nums[start];
dp[2] = max(nums[start], nums[start + 1]);
for (int i = start + 3; i < start + len + 1; ++i) {
//状态转移公式
dp[i - start] = max(dp[i - start - 1], dp[i - start - 2] + nums[i - 1]);
}
return dp[len];
}
};java代码
java
class Solution {
public int rob(int[] nums) {
int nums_len = nums.length;
if (nums_len == 0) return 0;
if (nums_len == 1) return nums[0];
return Math.max(help(nums, 0, nums_len - 1), help(nums, 1, nums_len - 1));
}
public int help(int[] nums, int start, int len) {
if (len == 0) {
return 0;
}
if (len == 1) {
return nums[start];
}
int[] dp = new int[len + 1];
// 边界条件
dp[1] = nums[start];
dp[2] = Math.max(nums[start], nums[start + 1]);
for (int i = start + 3; i < start + len + 1; ++i) {
// 状态转移公式
dp[i - start] = Math.max(dp[i - start - 1], dp[i - start - 2] + nums[i - 1]);
}
return dp[len];
}
}python代码
python
class Solution:
def rob(self, nums: List[int]) -> int:
nums_len = len(nums)
if nums_len == 0:
return 0
if nums_len == 1:
return nums[0]
return max(self.help(nums, 0, nums_len - 1), self.help(nums, 1, nums_len - 1))
def help(self, nums: List[int], start: int, length: int) -> int:
if length == 0:
return 0
if length == 1:
return nums[start]
dp = [0] * (length + 1)
# 边界条件
dp[1] = nums[start]
dp[2] = max(nums[start], nums[start + 1])
for i in range(start + 3, start + length + 1):
# 状态转移公式
dp[i - start] = max(dp[i - start - 1], dp[i - start - 2] + nums[i - 1])
return dp[length]复杂度分析
时间复杂度: 只需要遍历两遍数组nums,所以时间复杂度为O(n) ,n为nums的长度。
空间复杂度: 需要借助一个dp数组,空间复杂度为O(n) ,n为nums的长度。
实现优化
上面的空间复杂度是O(n) ,其实根据状态转移公式的特点,当前的状态只依赖前面的两个状态 ,我们可以不使用数组保存所有的状态,使用两个整型变量pre和next来实现help函数。
c++代码
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int nums_len = nums.size();
if (nums_len == 0) return 0;
if (nums_len == 1) return nums[0];
return max(help(nums, 0, nums_len - 1), help(nums, 1, nums_len - 1));
}
int help(vector<int>& nums, int start, int len) {
if (len == 0) {
return 0;
}
if (len == 1) {
return nums[start];
}
//边界条件
int pre = nums[start];
int next = max(nums[start], nums[start + 1]);
for (int i = start + 2; i < start + len; ++i) {
//状态转移公式
int temp = next;
next = max(pre + nums[i], next);
pre = temp;
}
return next;
}
};java代码
java
class Solution {
public int rob(int[] nums) {
int nums_len = nums.length;
if (nums_len == 0) return 0;
if (nums_len == 1) return nums[0];
return Math.max(help(nums, 0, nums_len - 1), help(nums, 1, nums_len - 1));
}
public int help(int[] nums, int start, int len) {
if (len == 0) {
return 0;
}
if (len == 1) {
return nums[start];
}
// 边界条件
int pre = nums[start];
int next = Math.max(nums[start], nums[start + 1]);
for (int i = start + 2; i < start + len; ++i) {
// 状态转移公式
int temp = next;
next = Math.max(pre + nums[i], next);
pre = temp;
}
return next;
}
}python代码
python
class Solution:
def rob(self, nums: List[int]) -> int:
nums_len = len(nums)
if nums_len == 0:
return 0
if nums_len == 1:
return nums[0]
return max(self.help(nums, 0, nums_len - 1), self.help(nums, 1, nums_len - 1))
def help(self, nums: List[int], start: int, length: int) -> int:
if length == 0:
return 0
if length == 1:
return nums[start]
# 边界条件
pre = nums[start]
next = max(nums[start], nums[start + 1])
for i in range(start + 2, start + length):
# 状态转移公式
temp = next
next = max(pre + nums[i], next)
pre = temp
return next优化后复杂度分析
时间复杂度: 只需要遍历两遍数组nums,所以时间复杂度为O(n) ,n为nums的长度。
空间复杂度: 只借助了几个整型变量,空间复杂度为O(1)。