算法day21|回溯理论基础、77. 组合（剪枝）、216.组合总和III、17.电话号码的字母组合

算法day21|回溯理论基础、77. 组合、216.组合总和III、17.电话号码的字母组合

• 回溯理论基础
• [77. 组合](#77. 组合)
• 77.组合（剪枝改进版）
• 216.组合总和III
• 17.电话号码的字母组合

回溯理论基础

• 回溯是递归的副产品，回溯函数也就是递归函数

• 回溯属于暴力解法，并不是高效的算法，使用剪枝操作可以优化，但是依然不高效

• 回溯本质上穷举，穷举所有所有的可能性，不放过任何一种情况。

• 所有的回溯问题都可以写成树形结构，用递归表示深度，用每个结点的子集来表示宽度并用for循环遍历。最后一般是再终止条件出返回。

• 可以解决的问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

• 模板：

  void backtracking(参数) {
      if (终止条件) {
          存放结果;
          return;
      }
  
      for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
          处理节点;
          backtracking(路径，选择列表); // 递归
          回溯，撤销处理结果
      }
  }

注意点：

• 返回值一般为void
• 参数很难一开始就完全确定，需要边写边加

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20

• 1 <= k <= n

  ---

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(int n, int k,int startIndex)
    {
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }
        for(int i=startIndex;i<=n;i++)
        {
            path.push_back(i);
            backtracking(n,k,i+1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
};

首先要自己画一个树形结构，不能光靠脑洞来想。如图(该图来自卡哥)：

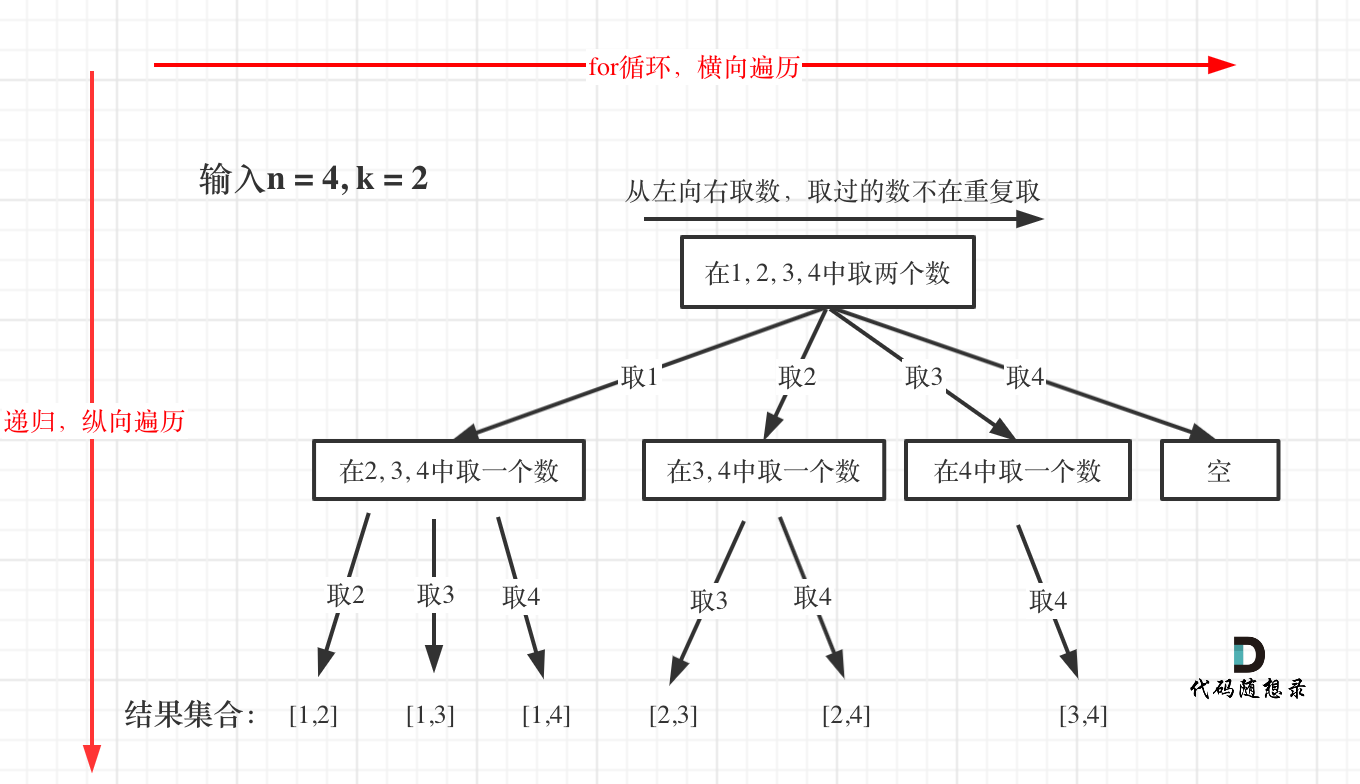
一次递归回溯完成的事：一开始在一个集合里面取一个数并放在path数组中，中间一般是递归，在最后在把在本层递归里面取的数弹出数组。也就是一次递归实际上就是对应图中的一个方框（即集合）。有多少个方框（集合）就有多少个过程递归，当然不含最后的终止条件递归的。

终止条件：与一些二叉树的题目类似，在终止条件记录最终要求的结果。

本题的回溯主要体现在pop的过程，其他逻辑与正常的递归类似。

77.组合（剪枝改进版）

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(int n, int k,int startIndex)
    {
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }
        for(int i=startIndex;i<=n-(k-path.size())+1;i++)
        {
            path.push_back(i);
            backtracking(n,k,i+1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
};

最大的区别就是for循环将 i<=n 改成了 i<=n-(k-path.size())+1 ，其中 k-path.size()表示最后的结果还需要k-path.size()个数，所以用**n-(k-path.size())**作为遍历的终点。如果不理解，可以先记住。

216.组合总和III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

• 2 <= k <= 9
• 1 <= n <= 60

本题不难，代码如下（含剪枝）：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    int vectorSum(vector<int> vec)
    {
        int sum=0;
        for(int i=0;i<vec.size();i++)
        sum+=vec[i];
        return sum;
    }
    void backtracking(int k, int n, int startIndex)
    {
        if(path.size()==k)
        {
            if(vectorSum(path)==n)
            result.push_back(path);
            return;
        }
        for(int i=startIndex;i<=9-(k-path.size())+1;i++)
        {
            path.push_back(i);
            backtracking(k,n,i+1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k,n,1);
        return result;
    }
};

17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

class Solution {
public:
    string letterMap[10]={
        " "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    string path;
    vector<string> result;
    void backtracking(string digits,int index)
    {
        if(index==digits.size())
        {
            result.push_back(path);
            return;
        }
        int start=digits[index]-'0';
        string letter=letterMap[start];
        for(int i=0;i<letter.size();i++)
        {
            path.push_back(letter[i]);
            backtracking(digits,index+1);
            path.pop_back();
        }
        return;
    }
    vector<string> letterCombinations(string digits) {
        if(digits=="")
        return result;
        backtracking(digits,0);
        return result;
    }
};

这题主要是两个难点：

• 如何将digits内的数字取 出来，并通过这个数字来映射字母呢？

答：首先引入index作为字符串digits的索引，用于对digits的遍历。当得到如digits[0]之后，用特定语法将其转化为int，即减去 '0'，字符型即可变成整数型如：

int start=digits[index]-'0';

然后，得到数字之后，建立建立二维数组，也就是字符串型的一维数组：

string letterMap[10]={" "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};

（要有这个意识：字符串本身就是一维数组，内部的数据类型是字符型，每一项都是字符，而整体是字符串）所以这里的字符串可以当成是二维数组。

• 如何在多个不同集合内做递归回溯呢

答：我们之前都是在一个集合里面折腾，这次其实是多个不同集合，该怎么办呢？正确的思路：寻找他们的根源 。读题发现，他们都来自于字符串digits，只要能对digits做一些处理，就完全可能实现递归回溯。

巧思：

backtracking(digits,index+1);

直接在函数里面加减，更加精巧灵动，又学了一招。