C/C++ 中的算术运算及其陷阱（详解，举例分析）

特立独行的猫a2024-09-10 8:19

在C/C++编程中，算术运算是非常基础且常用的操作。然而，这些看似简单的运算背后却隐藏着一些潜在的陷阱，如果不加以注意，可能会导致程序出现难以预料的错误。本文将探讨C/C++中常见的算术运算及其潜在的陷阱，并通过实例进行说明。

C/C++ 有自己特殊的算术运算规则，如整型提升和寻常算术转换，并且存在大量未定义行为，一不小心就会产生 bug，解决这些 bug 的最好方法就是熟悉整数性质以避免 bug。

bug复现

以下代码示例，猜猜看，运算结果是什么？ 都是unit16类型 ，0和65535+1 相等吗？

cpp 复制代码 
#include <iostream>

int main()
{
     std::cout<<"Hello World\n";
    
     uint16_t counter = 0;
     
     uint16_t value = 65535;
     
     if(counter == (value + 1)){
         std::cout<<"相等";
     }else{
         std::cout<<"不相等";
     }

    return 0;
}

以上输出的正确答案是不相等。

无符号数的溢出是合法的，有符号数溢出是未定义行为。上面利用整形溢出去跟0比较，这没问题。但问题出在另一个问题上，即整型提升。有网友说是隐式类型转换，也算是吧。准确的解释是整形提升。这个value65535，虽然它的类型是unit16，然而在算术运算时，出现溢出，整型提升，转为了int型，所以65535+1的结果并不是0！

关于整型提升

定义如下：

C11 6.3.1.1

If an int can represent all values of the original type (as restricted by the width, for a bit-field), the value is converted to an int; otherwise, it is converted to an unsigned int. These are called the integer promotions.

在算术运算中，秩小于等于int和unsigned int的整型（把它叫做小整型），如char、_Bool等转换为int或unsigned int，如果int可以表示该类型的全部值，则转换为unsigned int，否则转换为unsigned int。由于在 x86 等平台上，int 一定可以表示这些小整型的值，因此不论是有符号还是无符号，小整型都会隐式地转换为 int，不存在例外（otherwise 所说的情况）。

在某些平台上，int可能和short一样宽。这种情况下，int无法表示unsigned short的全部值，所以unsigned short要提升为unsigned int。这也就是标准中说的*"否则，它将转换为unsigned int"*。

cpp 复制代码 
// C++17
// 有符号数溢出是未定义行为，但在许多编译器上能看到正常的结果，
// 这里只是观察现象，请不要认为有符号数溢出是合法的
#include <cfloat>
#include <climits>
#include <cstdio>
#include <type_traits>
int main()
{
  signed char cresult, a, b;
  int iresult;
  a = 100;
  b = 90;
  // a，b 提升为整型，a + b = 190 在 int 表示范围内，没有溢出。
  // int 类型的 a + b 赋给表示范围更小的 char 类型 cresult（窄化），
  // 发生溢出，值为 190 - 256 = -66。
  cresult = a + b; /* C++17: cresult {a + b}; 编译器报错，不能将 int 窄化为 signed char */
  // a，b 提升为整型，a + b = 190 在 int 表示范围内，没有溢出。
  // int 类型的 a + b 赋给表示范围相同的 int 类型 iresult，没
  // 发生溢出，值为 190。
  iresult = a + b;
  printf("cresult: %dn", cresult);
  printf("cresult: %dn", iresult);

// ======== output ========
// cresult: -66
// cresult: 190

寻常算术类型 转换规则如下：

6.3.1.8 Usual arithmetic conversions

Many operators that expect operands of arithmetic type cause conversions and yield result types in a similar way. The purpose is to determine a common real type for the operands and result. For the specified operands, each operand is converted, without change of type domain, to a type whose corresponding real type is the common real type. Unless explicitly stated otherwise, the common real type is also the corresponding real type of the result, whose type domain is the type domain of the operands if they are the same, and complex otherwise. This pattern is called the usual arithmetic conversions:

  • First, if the corresponding real type of either operand is long double, the other operand is converted, without change of type domain, to a type whose corresponding real type is long double.
  • Otherwise, if the corresponding real type of either operand is double, the other operand is converted, without change of type domain, to a type whose corresponding real type is double.
  • Otherwise, if the corresponding real type of either operand is float, the other operand is converted, without change of type domain, to a type whose corresponding real type is float.
  • Otherwise, the integer promotions are performed on both operands. Then the following rules are applied to the promoted operands:
    • If both operands have the same type, then no further conversion is needed.
    • Otherwise, if both operands have signed integer types or both have unsigned integer types, the operand with the type of lesser integer conversion rank is converted to the type of the operand with greater rank.
    • Otherwise, if the operand that has unsigned integer type has rank greater or equal to the rank of the type of the other operand, then the operand with signed integer type is converted to the type of the operand with unsigned integer type.
    • Otherwise, if the type of the operand with signed integer type can represent all of the values of the type of the operand with unsigned integer type, then the operand with unsigned integer type is converted to the type of the operand with signed integer type.
    • Otherwise, both operands are converted to the unsigned integer type corresponding to the type of the operand with signed integer type.

在算术运算中，不仅整数要转换类型，浮点数也要转换类型。浮点数没有有符号/无符号之分，直接转换为能够容纳操作数的最小浮点类型即可，如单精度浮点数和双精度浮点数运算，单精度浮点数转换为双精度浮点数。

整数之间由于存在无符号/有符号的差异，转换稍微复杂一点：

  1. 进行整型提升
  2. 如果类型相同，不转换
  3. 如果符号相同，将秩低的类型转换为秩高的类型
  4. 如果无符号类型的秩高于或等于其他操作数，将其他操作数转换为该无符号数的类型
  5. 如果有符号数的类型可以表示其他操作数类型的全部值，将其他操作数转换为该有符号数的类型
  6. 如果以上步骤都失败，一律转换为无符号数，再进行上述步骤

算术类型转换是为了找到合理的公共类型，所以当整数符号相同时将较小的整型转换为较大的整型，将精度较小的浮点数转换为精度较大的浮点数。但 C 语言很古怪，当整型符号不同时会尝试将整型转换为无符号类型（无符号类型的秩不低于有符号类型时），这会导致负数被错误的当成非常大的正数。C 语言的算术类型转换很可能是一个失败的设计，会导致非常多难以发现的 bug，比如无符号和有符号数比较：

cpp 复制代码 
#include <stdio.h>
int main()
{
    unsigned int a = 100;
    int b = -100;
    printf("100 > -100: %dn", a > b); // b 被转换为 unsiged int，-100 变成一个很大的正数
    return 0;
}
// ===== output =====
100 > -100: 0

整型提升讲的是的小整型 转换为秩更高的unsiged int或int，当参加算术运算时发生，是寻常算术转换的第一步，因此可以认为是寻常算术类型转换的特例。结合之前的介绍的整形字面量，我们应该已经理解了 C/C++ 算术运算的完整过程：

  1. 推导出字面量的类型
  2. 进行寻常算术转换
  3. 计算

第一步中，如果字面量是十进制字面量，字面量会被推导为有符号数;如果是八进制、十六进制字面量，可能会被推导为无符号数。第二步中，可能会同时出现无符号数和有符号数，寻常算术转换可能会将有符号数转换为无符号数，一定要小心再小心。

不仅发生寻常算术类型转换可能导致 bug，误以为发生了寻常算术类型转换也可能导致 bug，就连 Apple 这样的巨头都在自己的安全编码规范中翻了车，详见Buggy Security Guidance from Apple：

cpp 复制代码 
// int n, m;
if (n > 0 && m > 0 && SIZE_MAX/n >= m) {
    size_t bytes = n * m;
    // allocate "bytes" space
}

Apple 的原意是先判断乘法是否溢出，再将乘积赋给一个足够宽的变量避免溢出，但这个实现有两个错误：

  • int型变量的最大值是INT_MAX而不是SIZE_MAX
  • n和m都是int型变量，乘积溢出后会被截取到int的表示范围内，然后再赋给bytes

所以，在涉及类型宽度不同的算术类型时要格外小心，可能会出现结果被截取后再赋给变量的情况。

有了这些知识，回头看这一节中的 stackoverflow 问题。第一个代码块中，两变量的类型是int和unsigned int，发生寻常算术类型转换，int转换为unsigned int，负数变正数 UINT_MAX - 1，相加后得到UINT_MAX，因此(1 - 2) > 0;第二个代码块中，两变量的类型是char和unsigned char，发生整型提升，转换为int，相加的到负数，因此(1 - 2) > 0。

再举一例

整型提升与寻常算术转换

再看一个 stackoverflow 上的提问Implicit type promotion rules，通过这个例子来了解 C/C++ 算术运算中的整型提升 （integer promotion ）和寻常算术转换 （usual arithmetic conversion ）。提问者编写了以下两段代码，发现在第一段代码中，(1 - 2) > 0，而在第二段代码中(1 - 2) < 0。这种奇怪的现象就是整型提升和寻常算术转换导致的。

cpp 复制代码 
unsigned int a = 1;
signed int b = -2;
if(a + b > 0)
    puts("-1 is larger than 0");
// ==============================================
unsigned short a = 1;
signed short b = -2;
if(a + b > 0)
    puts("-1 is larger than 0"); // will not print

整型提升和寻常算术转换涉及到整型的秩（优先级），规则如下：

  • 所有有符号整型的优先级都不同，即使宽度相同。

    假如int和short宽度相同，但int的秩大于short。

  • 有符号整型的秩大于宽度比它小的有符号整型的秩

    long long宽度为 64 比特，int宽度为32比特，long long的秩更大

  • long long的秩大于long，long的秩大于int，int的秩大于signed char

  • 无符号整型的秩等于对应的有符号整型

    unsigned int的秩等于对应的int

  • char的秩等于unsiged char和signed char

  • 标准整型的秩大于等于对应宽度的拓展整型

  • _Bool的秩小于所有标准整型

  • 枚举类型的秩等于对应整型

上面的规则看似复杂，但其实就是说：内置整型是一等公民，拓展整型是二等公民，_Bool是弟弟，枚举等同于整型。

算术溢出检测

(omega) 位整数的和需要 (omega + 1) 位才能表示，(w) 位整数的积需要 (2omega) 位才能表示，计算后 C/C++ 仅截取低 (omega) 位，可能会发生溢出。C/C++ 不会自动检测溢出，一旦发生溢出，程序就会在错误的状态中运行。

由于编译器会进行死代码消除 （dead code elimination ）和未定义行为消除 （undefined behavior elimination ），依赖 UB 的代码很可能会被编译器消除掉，即使没被消除掉，发生未定义行为就无法保证程序处于正确状态，参考It's Time to Get Serious About Exploiting Undefined Behavior。以一种错误的缓冲区溢出检测方法来说明编译器优化对代码的影响。

cpp 复制代码 
// 这个例子来自 https://www.kb.cert.org/vuls/id/162289
char buf[1024];
int len;
len = 1<<30;
// do something
if(buf+len < buf) // check
    // do something

如果len是一个负数，那么buf + len < buf一定为真。这个逻辑是对的，但 C 语言中数组越界是未定义行为，编译器可以忽略依赖未定义行为的代码，直接消除掉if语句，因此上面的检测实际上没有任何用处。因此必须在有符号数溢出之前进行检测。

对于无符号加法 (c = a + b)，溢出后 (c < aspace and space c < b);对于有符号加法 (c = a + b)，当且仅当 (a,b) 同号，但 (c) 与 (a, b) 符号相反时溢出，即 (a, b > 0 rightarrow c < 0 space 或 space a, b < 0 rightarrow c > 0)。注意，加法是一个阿贝尔群，不论是否溢出，(c - a) 都等于 (b)，所以不能以和减加数的办法检测溢出。

cpp 复制代码 
#include <limits.h>

int signed_int_add_overflow(signed int a, signed int b)
{
    // 检测代码不能导致有符号数溢出
    return ((b > 0) && (a > (INT_MAX - b))) || ((b < 0) && (a < (INT_MIN - b)));
}

int unsigned_int_add_overflow(unsigned int a, unsigned int b)
{
    // 无符号数溢出合法，检测代码可以依赖溢出的值
    unsigned int sum = a + b;
    return (sum < a) && (sum < b);
}

乘法发生溢出时，将 (2omega) 的积截取到 (w) 位，得到的积一定不等于正常的数学运算的积。

cpp 复制代码 
#include <limits.h>
#include <stdio.h>

int unsigned_int_multiply_overflow(unsigned int a, unsigned int b)
{
    if (a == 0 && b == 0) {
        return 0;
    }
    unsigned int product = a * b; // 无符号溢出是合法的
    return (a != 0) ? product / a == b : product / b == a;
}

int signed_int_multiply_overflow(signed int a, signed int b)
{
    // a 和 b 可能为负，也可能为正，需要考虑 4 种情况
    if (a > 0) {     // a is positive
        if (b > 0) { // a and b are positive
            if (a > (INT_MAX / b)) {
                return 1;
            }
        } else { // a positive, b nonpositive
            if (b < (INT_MIN / a)) {
                return 1;
            }
        }            // a positive, b nonpositive
    } else {         // a is nonpositive
        if (b > 0) { // a is nonpositive, b is positive
            if (a < (INT_MIN / b)) {
                return 1;
            }
        } else { // a and b are nonpositive
            if ((a != 0) && (b < (INT_MAX / a))) {
                return 1;
            }
        } // End if a and b are nonpositive
    }     // End if a is nonpositive
    return 0;
}

位运算技巧

位运算是 C/C++ 的一大利器，存在大量的技巧，我不是这方面的高手，这里只是介绍几个最近学习中碰到的让我打开眼界的技巧，感兴趣的可以参考这份清单（我没有看）Bit Twiddling Hacks。

  • 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
cpp 复制代码 
// 利用异或消除相同元素
int SingleNumber(std::vector<int>& nums)
{
  int ret = 0;
  for (ssize_t i = nums.size() - 1; i >= 0; --i) {
    ret ^= nums[i];
  }
  return ret;
}
  • 消去二进制数最低位的 1

可以观察到，整数减一会消去最低位的 1（0 反转为 1），低位的 0 全部反转为 1，因此val & (val - 1)可以消去最低位的 1 且不再后面生成新的 1。

cpp 复制代码 
unsigned int val = /* something */;
val &= (val - 1); /* 消去最低位的 1 */

利用这个性质，可以快速计算出二进制数中 1 的个数：

cpp 复制代码 
int CountOfBinaryOne(unsigned int val) {
    int cnt = 0;
    while (val != 0) {
        val &= (val - 1);
        ++cnt
    }
    return cnt;
}

当整数是 2 的整数幂时，二进制表示中仅有一个 1，所以这个方法还可以用来快速判断2 的幂。

cpp 复制代码 
int IsPowerOf2(unsigned int val) {
    return (val & (val - 1)) == 0;
}
  • 找出不大于 N 的 2 的最大幂

从二进制的角度看，求不大于 N 的最大幂就是将 N 位数最高的 1 以下的 1 全部清空。可以不断消除低位的 1，直到整数为 0，整数变成 0 之前的值就是不大于 N 的 2 的最大幂。

这里还有更好的方法，在 O(1) 时间， O(1) 空间实现功能。先将最高位的 1 以下的比特全部置为 1，然后加一（清空全部为 1 的比特，并将进位），右移一位。举例如下：

01001101 --> 01111111 --> 01111111 + 1 --> 10000000 --> 01000000

代码如下：

cpp 复制代码 
unsigned int MinimalPowerOf2(unsigned int val) {
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    return (n + 1) >> 1;
}

这个实现无法处理最高位为 1 的情况，这时val会被或操作变成UINT_MAX，最后(n + 1) >> 1得到0。正确的版本如下：

cpp 复制代码 
unsigned int MinimalPowerOf2(unsigned int n)
{
    if ((int)n < 0) { // 最高位为 1
        return 1 << 31;
    }
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    return (n + 1) >> 1;
}

整数溢出

整数溢出是C/C++编程中常见的一个陷阱。当一个整数变量的值超过了其类型所能表示的最大值时，就会发生溢出，导致结果变得不可预测。

示例代码

cpp 复制代码 
#include <stdio.h>

int main() {
    int a = 2147483647; // 这是int类型的最大值
    int b = 1;
    int result = a + b; // 这里会发生溢出
    printf("Result: %d\n", result); // 输出结果会是-2147483648
    return 0;
}

在这个例子中，a的值是int类型的最大值，加上b的值1后，结果超出了int类型的表示范围，导致溢出，结果变成了负数。

C/C++ 整数的阴暗角落

C/C++ 期望自己可以在所有机器上运行，因此不能在语言层面上把整数的编码、性质、运算规定死，这让 C/C++ 中存在许多未规定的阴暗角落和未定义行为。许多东西依赖于编译器、操作系统和处理器，这里通称为运行平台。

  • 标准没有规定整数的编码，编码方式依赖于运行平台。

  • char是否有符号依赖于运行平台，编译器有选项可以控制，如 GCC 的 -fsign-char。

  • 移位大小必须小于整数宽度，否则是未定义行为。

  • 无符号数左移 K 位结果为原来的 2^K 次方，右移 K 位结果为原来的数除 2^K 次方。仅允许对值非负的有符号数左移右移，运算结果同上，对负数移位是未定义的。

  • 标准仅规定了标准内置整数类型（如int等）的最小宽度和大小关系（如long不能小于int），但未规定具体大小，如果要用固定大小的整数，请使用拓展整数类型（如uint32_t）等。

  • 无符号数的溢出是合法的，有符号数溢出是未定义行为

整型字面量

常常有人说 C/C++ 中的整数字面量类型是int，但这种说法是错误的。C/C++ 整形字面量究竟是什么类型取决于字面量的格式和大小。StackOverflow 上有人问为什么在 C++ 中(-2147483648> 0)返回true，代码片段如下：

cpp 复制代码 
if (-2147483648 > 0) {
    std::cout << "true";
} else {
    std::cout << "false";
}

现在让我们来探索为什么负数会大于 0。一眼看过去，-2147483648似乎是一个字面量（32 位有符号数的最小值），是一个合法的int型变量。但根据 C99 标准，字面量完全由十进制（1234）、八进制（01234）、十六进制（0x1234）标识符组成，因此可以认为只有非负整数才是字面量 ，负数是字面量的逆元。在上面的例子中，2147483648是字面量，-2147483648是字面量2147483648的逆元。

字面量的类型取决于字面量的格式和大小，C++11（N3337 2.14.2）规则如下：

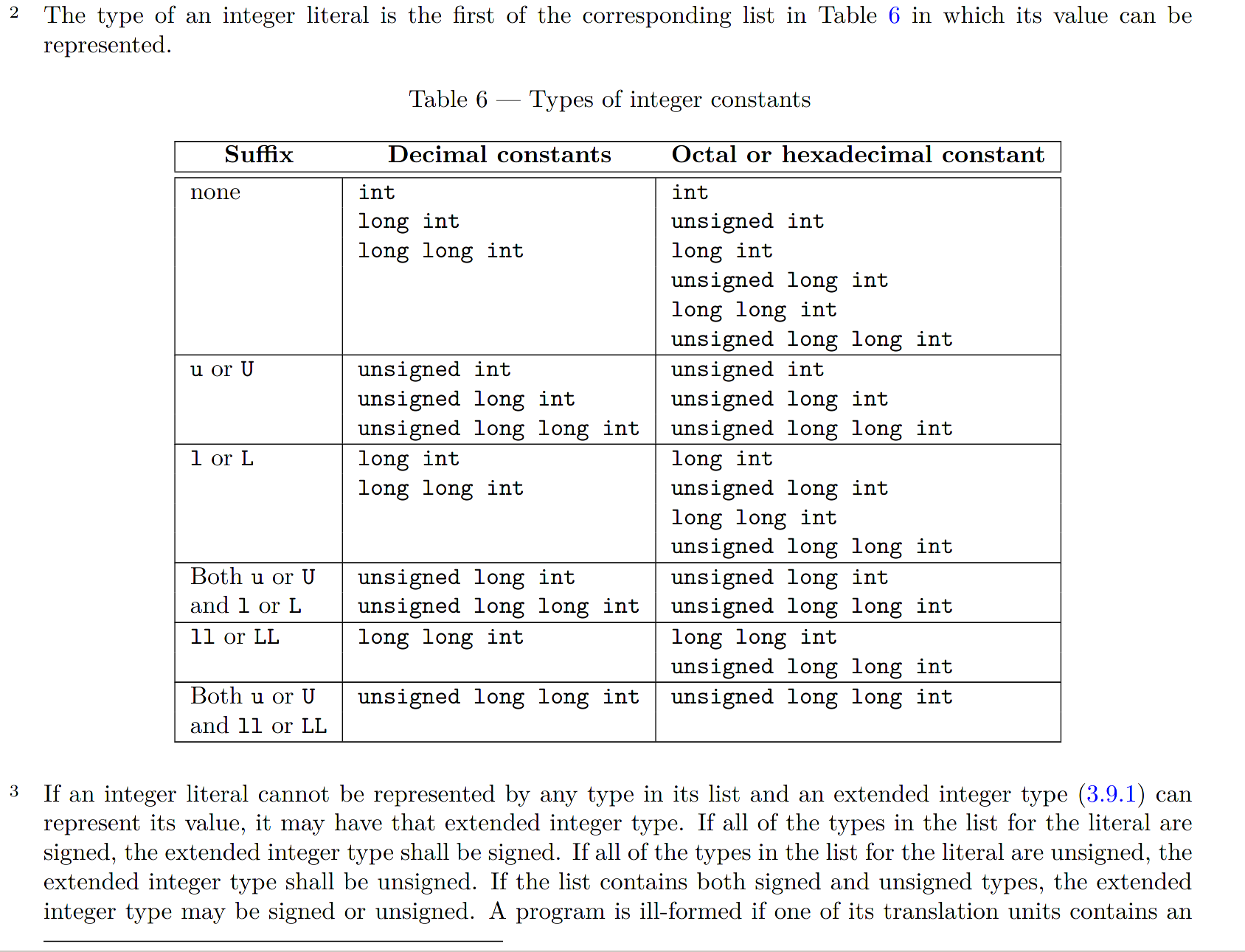
对于十进制字面量，编译器自动在int、long、long long中查找可以容纳该字面量的最小类型，如果内置整型无法表示该值，在拓展整型中查找能表示该值的最小类型;对于八进制、十六进制字面量，有符号整型无法表示时会选择无符号类型。如果没有足够大的内置/拓展整型，程序是错误的，GCC/Clang 会发出警告。

在 C89/C++98 没有long long和拓展整型，因此在查找完long后查找unsigned long。

现在再看上面的代码段就很清晰了，在 64 位机上，不论是 C89/C++98 还是 C99/C++11，都能找到容纳该值的long类型（8 字节），因此打印false。在 32 位机上，long占据 4 个字节无法容纳字面量，在 C89/C++98 下，2147483648的类型为unsigned long，逆元-2147483648是一个正数（2^32 - 2147483648），打印true;在 C99/C++11 下，2147483648的类型为long long，逆元-2147483648是一个负数（-2147483648），打印false。

经过以上分析，可以判断出提问者是在 32 位机上使用 C++98 做的实验。

和字面量有关的另一个有意思的问题是INT_MIN的表示方法。《深入理解计算机系统（第 3 版）》2.2.6 中介绍的代码如下：

cpp 复制代码 
/* Minimum and maximum values a 'signed int' can hold. */
#define INT_MAX 2147483647
#define INT_MIN (-INT_MAX - 1)

《深入理解计算机系统》没有给出解释，但这种写法很显然为了避免宏INT_MIN被推导为long long（C99/C++11）或unsigned long（C89/C++98）。

浮点数精度问题

浮点数在计算机中的表示是近似的，而不是精确的。因此，在进行浮点数运算时，可能会遇到精度问题，导致结果与预期不符。

示例代码

cpp 复制代码 
#include <stdio.h>

int main() {
    float a = 0.1;
    float b = 0.2;
    float result = a + b;
    printf("Result: %.10f\n", result); // 输出结果会是0.3000000119
    return 0;
}

在这个例子中，a和b的值分别是0.1和0.2，但它们的和并不是精确的0.3，而是一个接近0.3的值。

除零错误

在C/C++中，除法运算中除数不能为零，否则会导致程序崩溃或产生未定义行为。

示例代码

cpp 复制代码 
#include <stdio.h>

int main() {
    int a = 10;
    int b = 0;
    int result = a / b; // 这里会发生除零错误
    printf("Result: %d\n", result);
    return 0;
}

在这个例子中，b的值为0，进行除法运算时会导致除零错误，程序可能会崩溃。

类型转换问题

在进行算术运算时，不同类型的数据之间可能会发生隐式类型转换，这可能会导致结果与预期不符。

示例代码

cpp 复制代码 
#include <stdio.h>

int main() {
    int a = 5;
    float b = 2.5;
    float result = a + b; // a会被隐式转换为float类型
    printf("Result: %.2f\n", result); // 输出结果会是7.50
    return 0;
}

在这个例子中，a是int类型，b是float类型，进行加法运算时，a会被隐式转换为float类型，结果是7.5。

总结

C/C++中的算术运算虽然基础，但其中隐藏着许多陷阱。程序员在进行算术运算时，需要特别注意整数溢出、浮点数精度问题、除零错误以及类型转换问题，以避免程序出现难以预料的错误。通过本文的介绍和示例代码，希望读者能够更好地理解和避免这些陷阱，编写出更加健壮的C/C++程序。

  1. 尽可能不要混用无符号数和有符号数，如果一定要混用，请小心谨慎。

  2. 在涉及不同大小的数据类型时要小心，可能存在溢出和截断。

  3. 只要存在有符号数就要考虑溢出导致的未定义行为和可能的符号反转。

  4. 尽量不对小于int的整数类型执行算术运算，可能溢出和涉及整型提升。

  5. 如果要利用整数溢出，必须使用无符号数。

参考

https://www.cnblogs.com/kongj/p/14612362.html

C/C++ 中的算术及其陷阱 | 高性能架构探索

相关推荐
红龙创客6 分钟前
某狐畅游24校招-C++开发岗笔试（单选题）
开发语言·c++
Lenyiin8 分钟前
第146场双周赛：统计符合条件长度为3的子数组数目、统计异或值为给定值的路径数目、判断网格图能否被切割成块、唯一中间众数子序列 Ⅰ
c++·算法·leetcode·周赛·lenyiin
郭wes代码15 分钟前
Cmd命令大全（万字详细版）
python·算法·小程序
scan72430 分钟前
LILAC采样算法
人工智能·算法·机器学习
菌菌的快乐生活1 小时前
理解支持向量机
算法·机器学习·支持向量机
大山同学1 小时前
第三章线性判别函数（二）
线性代数·算法·机器学习
axxy20001 小时前
leetcode之hot100---240搜索二维矩阵II（C++）
数据结构·算法
黑客Ash1 小时前
安全算法基础（一）
算法·安全
yuanbenshidiaos2 小时前
c++---------数据类型
java·jvm·c++
十年一梦实验室2 小时前
【C++】sophus : sim_details.hpp 实现了矩阵函数 W、其导数，以及其逆 (十七)
开发语言·c++·线性代数·矩阵
热门推荐
01〔AI 绘画〕Stable Diffusion 之 解决绘制多人或面部很小的人物时面部崩坏问题 篇02YOLOv8训练好模型后，追加轮数继续训练、或者提前终止训练，缩减训练轮数03玄机平台应急响应—webshell查杀04机器人编程怎么入门？05HCIA-datacom数通题库和录播视频资料06Docker 夺命连环 15 问07SQL 主从数据库实时备份08校验 GPT-4 真实性的三个经典问题：快速区分 GPT-3.5 与 GPT-4，并提供免费测试网站09(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明10VSCode插件 —— Cody AI （免费AI助手！）