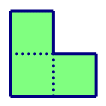
拼图
给出一个 n × m n \times m n×m 的方格图,现在要用如下 L L L 型的积木拼到这个图中,使得方格图正好被拼满,请问总共有多少种拼法。
其中,方格图的每一个方格正好能放积木中的一块。
积木可以任意旋转。
输入格式
输入的第一行包含两个整数 n , m n, m n,m,表示方格图的大小。
输出格式
输出一行,表示可以放的方案数,由于方案数可能很多,所以请输出方案数除以 1 0 9 + 7 10^9 + 7 109+7 的余数。
数据范围
在评测时将使用 10 10 10 个评测用例对你的程序进行评测。
评测用例 1 1 1 和 2 2 2 满足: 1 ≤ n ≤ 30 1 \le n \le 30 1≤n≤30, m = 2 m=2 m=2。
评测用例 3 3 3 和 4 4 4 满足: 1 ≤ n , m ≤ 6 1 \le n, m \le 6 1≤n,m≤6。
评测用例 5 5 5 满足: 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100, 1 ≤ m ≤ 6 1 \le m \le 6 1≤m≤6。
评测用例 6 6 6 和 7 7 7 满足: 1 ≤ n ≤ 1000 1 \le n \le 1000 1≤n≤1000, 1 ≤ m ≤ 6 1 \le m \le 6 1≤m≤6。
评测用例 8 、 9 8、9 8、9 和 10 10 10 满足: 1 ≤ n ≤ 1 0 15 1 \le n \le 10^{15} 1≤n≤1015, 1 ≤ m ≤ 7 1 \le m \le 7 1≤m≤7。
输入样例:
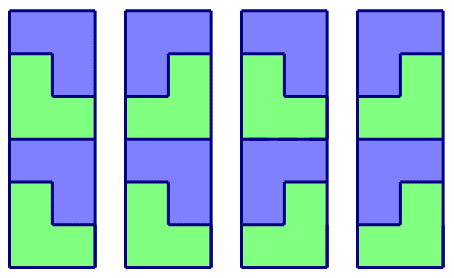
6 2输出样例:
4样例解释
四种拼法如下图所示:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 130, MOD = 1e9 + 7;
LL n;
int m;
int w[N][N];
void dfs(int x, int y, int u)
{
if (u == m) w[x][y] ++ ;
else if (x >> u & 1) dfs(x, y, u + 1);
else
{
if (u && !(y >> u & 1) && !(y >> u - 1 & 1))
dfs(x, y + (1 << u) + (1 << u - 1), u + 1);
if (u + 1 < m && !(y >> u & 1) && !(y >> u + 1 & 1))
dfs(x, y + (1 << u) + (1 << u + 1), u + 1);
if (u + 1 < m && !(x >> u + 1 & 1))
{
if (!(y >> u & 1)) dfs(x, y + (1 << u), u + 2);
if (!(y >> u + 1 & 1)) dfs(x, y + (1 << u + 1), u + 2);
}
}
}
void mul(int c[][N], int a[][N], int b[][N])
{
static int tmp[N][N];
memset(tmp, 0, sizeof tmp);
for (int i = 0; i < 1 << m; i ++ )
for (int j = 0; j < 1 << m; j ++ )
for (int k = 0; k < 1 << m; k ++ )
tmp[i][j] = (tmp[i][j] + (LL)a[i][k] * b[k][j]) % MOD;
memcpy(c, tmp, sizeof tmp);
}
int main()
{
cin >> n >> m;
for (int i = 0; i < 1 << m; i ++ )
dfs(i, 0, 0);
int res[N][N] = {0};
res[0][(1 << m) - 1] = 1;
while (n)
{
if (n & 1) mul(res, res, w);
mul(w, w, w);
n >>= 1;
}
cout << res[0][(1 << m) - 1] << endl;
return 0;
}蒙德里安的梦想
求把 N × M N \times M N×M 的棋盘分割成若干个 1 × 2 1 \times 2 1×2 的长方形,有多少种方案。
例如当 N = 2 , M = 4 N=2,M=4 N=2,M=4 时,共有 5 5 5 种方案。当 N = 2 , M = 3 N=2,M=3 N=2,M=3 时,共有 3 3 3 种方案。
如下图所示:

输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 N N N 和 M M M。
当输入用例 N = 0 , M = 0 N=0,M=0 N=0,M=0 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
1 ≤ N , M ≤ 11 1 \le N,M \le 11 1≤N,M≤11
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0输出样例:
1
0
1
2
3
5
144
51205朴素写法,1000ms
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;
long long f[N][M];
bool st[M];
int main()
{
while (cin >> n >> m, n || m)
{
for (int i = 0; i < 1 << n; i ++ )
{
int cnt = 0;
st[i] = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
if (cnt & 1) st[i] = false;
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) st[i] = false;
}
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; i ++ )
for (int j = 0; j < 1 << n; j ++ )
for (int k = 0; k < 1 << n; k ++ )
if ((j & k) == 0 && st[j | k])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}去除无效状态的优化写法,230ms
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 12, M = 1 << N;
int n, m;
LL f[N][M];
vector<int> state[M];
bool st[M];
int main()
{
while (cin >> n >> m, n || m)
{
for (int i = 0; i < 1 << n; i ++ )
{
int cnt = 0;
bool is_valid = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
if (cnt & 1)
{
is_valid = false;
break;
}
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) is_valid = false;
st[i] = is_valid;
}
for (int i = 0; i < 1 << n; i ++ )
{
state[i].clear();
for (int j = 0; j < 1 << n; j ++ )
if ((i & j) == 0 && st[i | j])
state[i].push_back(j);
}
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; i ++ )
for (int j = 0; j < 1 << n; j ++ )
for (auto k : state[j])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}