全文链接:https://tecdat.cn/?p=37668
分析师:Aijun Zhang
在当今的金融领域,量化交易正凭借其科学性和高效性逐渐成为主流投资方式之一。随着大数据技术的蓬勃发展,量化交易借助先进的数学模型和计算机分析能力,摒弃了人的主观判断,通过挖掘海量历史数据来锁定各种可能带来超额收益的 "高概率" 事件,从而有效降低投资者在市场波动中因情绪影响而做出非理性决策的风险**(** 点击文末"阅读原文"获取完整代码数据******** )。
在众多量化交易方法中,神经网络和机器学习方法的应用尤为引人关注。本文介绍了利用 BP 神经网络进行股价预测,通过构建特殊的交易策略在复杂的市场环境中(如黄金和比特币市场)进行投资交易,并结合深度神经网络(DNN)、循环神经网络(RNN)、循环卷积神经网络(RCNN)以及决策树、SVM、回归等多种机器学习方法在金融交易中的深入探索的实例代码和数据,不仅为金融交易提供了新的思路,而且有望构建出更高效、更智能的交易策略。本文将详细阐述这些方法在金融交易中的应用与实践。
BP神经网络的股价预测与决策建议模型、移动平均线交叉法模型量化投资
随着大数据技术的飞速发展,量化交易作为新兴的 投资方式,受到了更多投资者的青睐。 量化交易是指一种方法 用先进的数学模型代替人的主观判断,并使用计算机 分析海量历史数据的技术。 它选择了各种"高概率"事件 可以带来超额收益来制定策略,大大降低了投资者的影响 市场波动时避免做出非理性的投资决策 极度狂热或悲观。 我们选择了其中一些方法来为我们的战略做出贡献。
项目说明:
2016 年 9 月 11 日,您将从 1000 美元开始。 您将使用五年交易期,从 2016 年 9 月 11 日至 2021 年 9 月 10 日。 在每个交易日,交易者将拥有一个由现金组成的投资组合, 黄金和比特币 [C, G, B] 分别以美元、金衡盎司和比特币表示。 最初的 状态为 [1000, 0, 0]。 每笔交易(购买或销售)的佣金成本为 交易金额。 假设 αgold = 1% 和 αbitcoin = 2%。 持有资产没有成本。请注意,比特币可以每天交易,但黄金仅在市场开放日交易。
模型介绍:
使用 BP 神经网络模型进行预测。使用每连续5个交易日的价格预测第6个交易日的价格。即当前交易日的价格与前四个交易日的价格为 用于预测下一个交易日的价格。在黄金交易中,如果遇到止损交易 期间,将被跳过,例如 9/11、9/12/、9/15、9/16、9/17。这五个中的 9/13 和 9/14 交易日为停牌期,以上5天为5天 连续交易日。那么,因为标题要求只能获取当前交易日的信息 使用,在模型训练中建立时间序列模型。对于每个新的交易日, 将连续 5 个交易日的价格与今天生成的新价格相加 原始训练集生成新的训练集进行训练。最后,对于每个新的交易日,交易日的价格和交易日的价格 前4天用于预测,下一个交易日的价格。
模型建立:
通过建立一个 BP 神经网络,迭代地调整权重来确定 用于预测计算的权重矩阵。训练集: 输入层是一个 5*x 的矩阵(x 是当前交易日的总数,随着 时间)。内容为连续5个交易日的价格。输出层是一个 1*x 矩阵(x 与上述相同)。内容为连续5个交易日后第6个交易日的价格 days.BP神经网络框架: 它由输入层、隐藏层和输出层组成,其中隐藏层 一共有3层,所以BP神经网络框架是一个5层的神经网络,而 节点分别为 5、100、50、25 和 1。激活函数: 激活函数使用"Relu"函数。学习率: lr = 0.001 最大迭代次数: 1000 次 定时训练策略: 由于本次培训以5个交易日为窗口,培训期从5日开始 黄金和比特币交易日之后的交易日。以第一次训练迭代为例,从第一个交易日到 第五个交易日作为输入层,第六个交易日作为输出层 为了训练。所得模型用于预测第 7 个交易日的数据和 第2至第6个交易日预测第7个交易日的预测数据。 9 以第二次迭代为例,第 1 至第 5 个交易日的价格和 第 2 至第 6 个交易日的价格作为输入层, 第 6 和第 7 个交易日作为第一次训练的模型的输出层。进行训练以获得模型。使用第3至第7个交易日的价格进行预测 第8个交易日的价格得到预测结果。以此类推直到最后。模型预测结果如下。
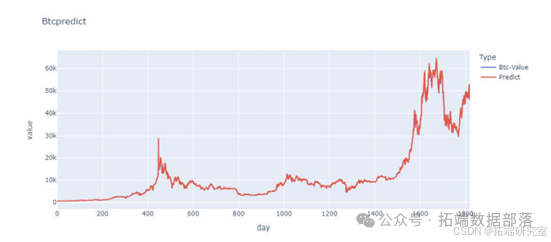
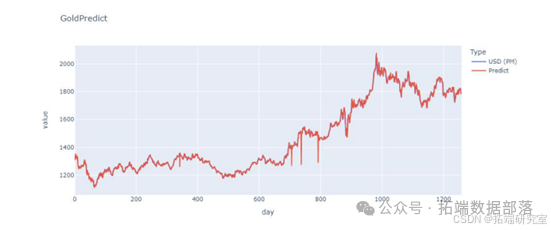
交易策略:
以建筑采购日、成交日、成交前价格的形式,交易日满足设定要求时,交易日记为购买日。设置了四个买入日策略,包括 5 天和 10 天移动平均线交叉法、追涨策略、抄底策略、大规模上涨战略。
-
5 天和 10 天移动平均线交叉法,通过计算每连续 5 天和每连续 10 天价格,得到 5 日线和 10 天线。一个交易日的 5 天点以交易日前 4 天的价格和当天的平均价格,10 天点是交易日前 9 天及当日价格。当 5 日线向上穿越 10 日线时,认为有上升趋势,与交叉点相邻的下一个交易日为交易日。
-
抄底策略是如果连续四个交易日下跌,且第四个交易日的预测模型预测下一个交易日将下跌,则将下一个交易日记录为购买日。例如,9/17 - 9/21 的实际价值下跌,而 9/21 的预测模型预测下跌 9/22,然后将 9/22 记录为购买日。
-
大涨策略,跌破 5 日线和 10 日线,连续三个交易日 5 日线和 10 日线上涨将记录第三个交易日为买入日。例如,9/17 - 9/20 君城上升趋势的 5 日线和 10 日线将记录 9/20 作为购买日。
综上所述,该交易模式下的购买策略将从预测模型和财务知识中获得的采购天数,获得预测购买之日。因为对购买日期的预测是根据变更交易日之前的数据计算预测,满足标题的要求。最后,当事务按照时间运行时,只要到了购买日期就进行购买事务。
因为在这个交易中设置了买点,但卖点不能通过 1 天的预测,所以决定建立一个固定的订单系统进行交易。当购买黄金或比特币时,相应的购买金额和黄金或比特币的市场价格被视为订单。随着交易日的更新和实盘的更新 value,跟踪每个订单的收益率,当 B - P 和 G - P 满足一定利润和损失率时卖出。虽然黄金和比特币的整体 G - D 和 B - D 是固定的,但将进行阶段调谐以找到最佳 B - P、G - P、B - D 和 G - D。最后,购买策略给出的可以进行购买的交易日由卖出策略自动卖出。给出最后持有的比特币和黄金的总量总计 5 年的美元和当前总金额。
优化策略
通过动态调整 B - P、D - P、B - D 和 G - D 的量。B - P 的盈利点至少大于 4%。因为单笔黄金交易的手续费是 1%,比特币是 2%。而 G - D、B - D 不能小于 10,不能大于 1000。
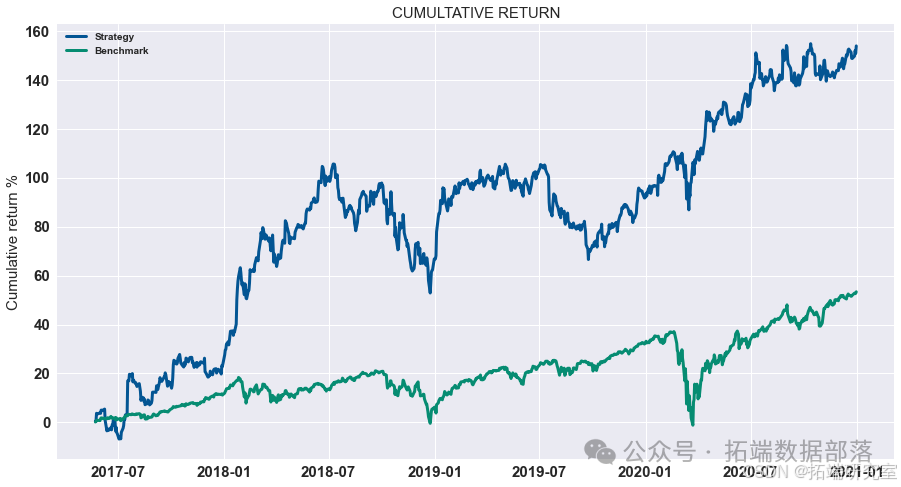
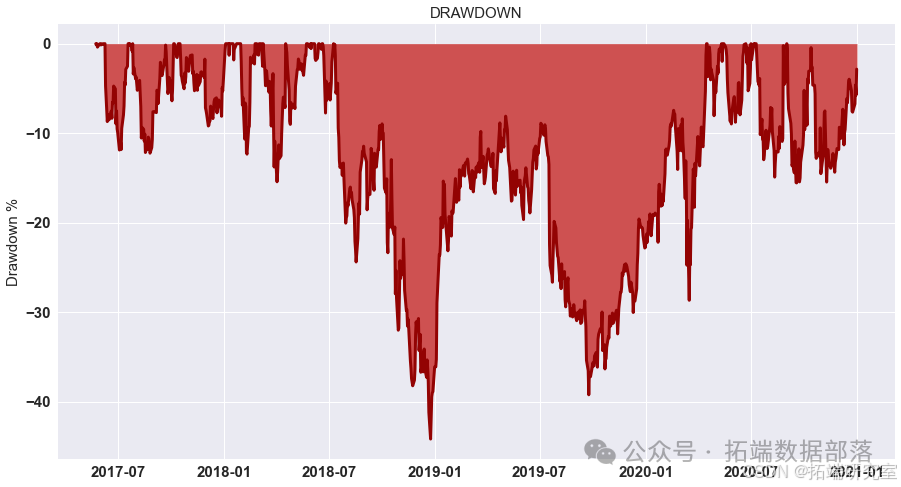
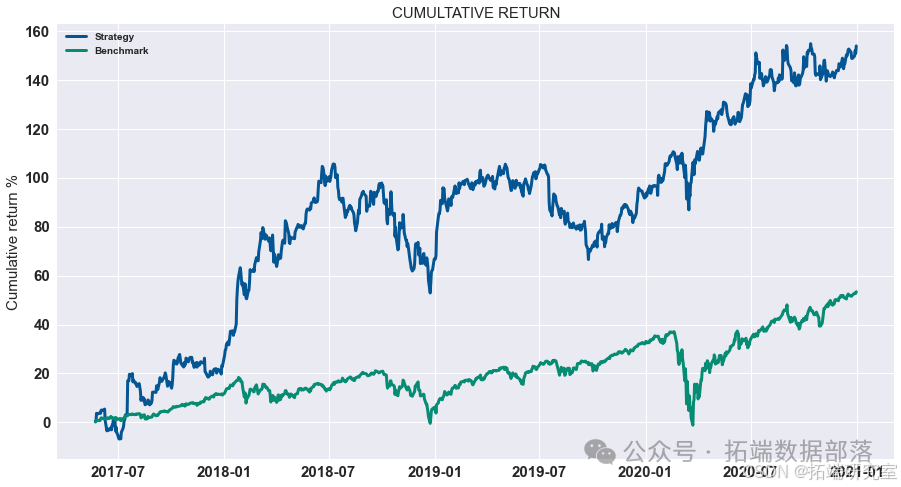
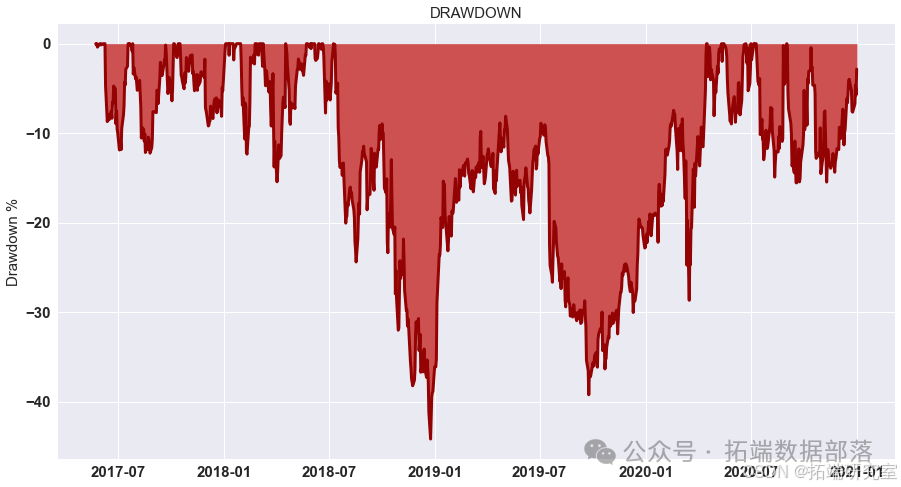
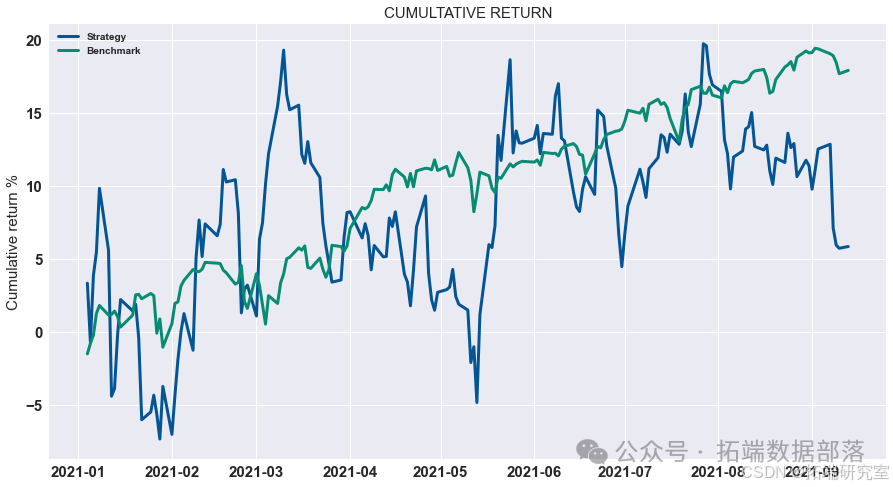
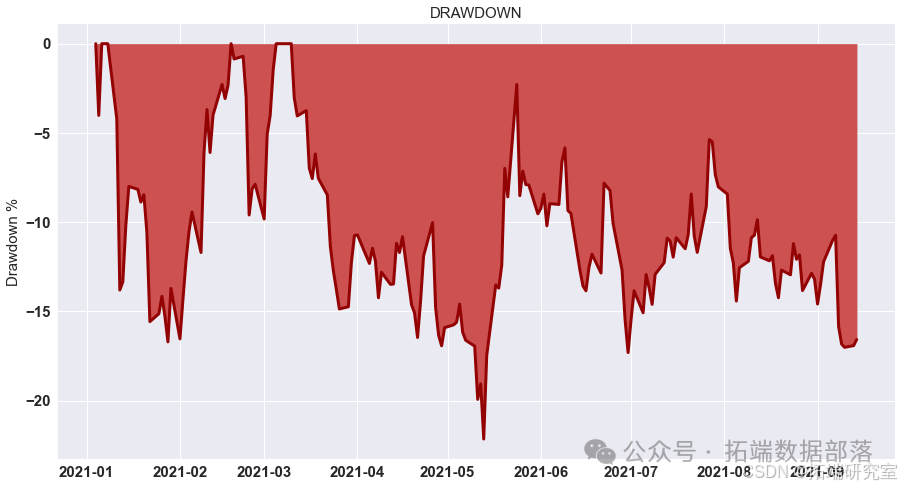
结果
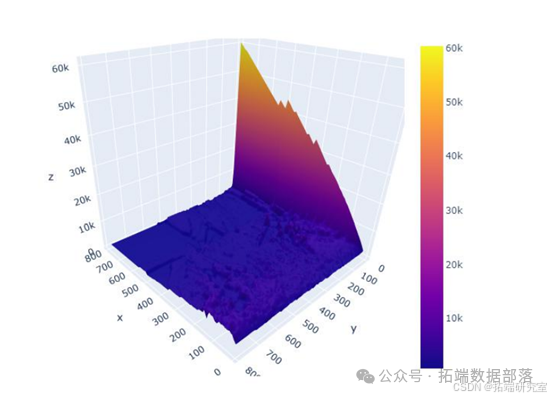
我们计算了G-D和B-D(X代表B-D,Y 代表 G-D,Z 代表最终利润)参数并显示所有可能性。 如图所示,在最高点,G-D=10,B-D=790。 在这种情况下,我们投入了最多 我们在比特币市场上的资金,这是可以理解的。 如果比特币的未来趋势 市场可以预见,大量资金投入比特币市场是合理的。 在 B-P 和 D-P 的计算中,我们发现前面的组合仍然有效。 到目前为止,在 第二组模型,也确定了四个参数,G-D=10,B-D=790,B-P=1.1,D-P=0.85。 那是有风险的
深度神经网络DNN、RNN、RCNN及多种机器学习方法在金融交易中的策略探索 |附数据代码
深度神经网络(DNN)
在深度学习领域中,深度神经网络(DNN)具有重要的地位。首先来了解一下 DNN 背后的关键概念。介绍了 DNN 背后的直觉,包括前向传播、梯度下降和反向传播。前向传播是数据在神经网络中从输入层经过一系列隐藏层到输出层的过程。梯度下降是一种优化算法,用于寻找网络的最优参数,通过计算损失函数对参数的梯度,然后沿着梯度的反方向更新参数,以最小化损失函数。反向传播则是计算损失函数对参数梯度的算法,从输出层开始,将误差反向传播到输入层,通过链式法则计算每个参数的梯度。
即用于分类的 DNN。是数据准备阶段。首先,通过以下代码导入苹果公司(AAPL)股票数据并进行处理:
go
df = yf.download("AAPL", end="2021-01-01")\[\["Adj Close"\]\].pct_change(1)
df.columns = \["returns"\]这里使用yfinance库下载股票数据,计算收益率并命名为"returns"列。然后进行特征工程,如下代码所示:
go
df\["returns t-1"\] = df\[\["returns"\]\].shift(1)
df\["mean returns 15"\] = df\[\["returns"\]\].rolling(15).mean().shift(1)
df\["mean returns 60"\] = df\[\["returns"\]\].rolling(60).mean().shift(1)
df\["volatility returns 15"\] = df\[\["returns"\]\].rolling(15).std().shift(1)
df\["volatility returns 60"\] = df\[\["returns"\]\].rolling(60).std().shift(1)分别创建了前一日收益率、15 日平均收益率、60 日平均收益率、15 日收益率波动率和 60 日收益率波动率等特征。接着,删除缺失值:
go
df = df.dropna()之后,按照 80%的比例划分训练集和测试集:
go
split = int(0.80*len(df))
X_train = df\[\["returns t-1", "mean returns 15", "mean returns 60",
"volatility returns 15",
"volatility returns 60"\]\].iloc\[:split\]
y\_train\_reg = df\[\["returns"\]\].iloc\[:split\]
y\_train\_cla = np.round(df\[\["returns"\]\].iloc\[:split\]+0.5)
X_test = df\[\["returns t-1", "mean returns 15", "mean returns 60",
"volatility returns 15",
"volatility returns 60"\]\].iloc\[split:\]
y\_test\_reg = df\[\["returns"\]\].iloc\[split:\]
y\_test\_cla = np.round(df\[\["returns"\]\].iloc\[split:\]+0.5)创建了训练集和测试集的特征和目标变量。最后进行数据标准化:
go
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X\_train\_scaled = sc.fit\_transform(X\_train)
X\_test\_scaled = sc.transform(X_test)使用StandardScaler类对数据进行标准化处理,确保不同特征具有相同的尺度。
实现用于分类任务的 DNN。首先设置随机种子确保结果可重复性:
go
np.random.seed(15)然后导入所需的库:
go
import tensorflow
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout定义隐藏层数量为 1:
go
nb\_hidden\_layer = 1初始化顺序模型:
go
classifier = Sequential()通过循环添加隐藏层和 Dropout 层:
go
for _ in range(nb\_hidden\_layer):
classifier.add(Dense(75, input\_shape = (X\_train.shape\[1\],), activation="relu"))这里添加了一个包含 75 个神经元的隐藏层,输入形状根据训练集特征数量确定,激活函数为"relu",可以有效地引入非线性。接着添加输出层:
go
classifier.add(Dense(1, activation="sigmoid"))输出层包含 1 个神经元,激活函数为"sigmoid",适用于二分类任务。然后编译模型:
go
classifier.compile(loss="binary_crossentropy", optimizer="adam")使用"binary_crossentropy"作为损失函数,"adam"作为优化器。最后进行训练:
go
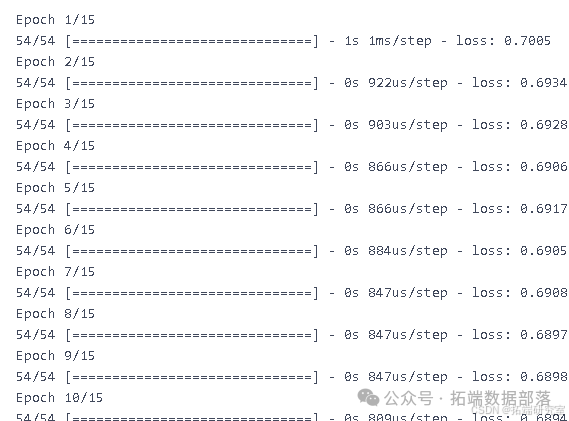
classifier.fit(X\_train\_scaled, y\_train\_cla, epochs=15, batch_size=150, verbose=1)使用标准化后的训练集进行训练,设置训练轮数为 15,批次大小为 150,并显示训练过程中的信息。
综上所述,通过合理的数据准备和模型构建,可以有效地利用深度神经网络进行分类任务。
预测与策略计算
在金融数据分析等领域中,预测和回测是非常关键的环节。以下是相关的实现过程:
(一)创建整个数据集的预测
- 分类预测
-
首先,对于分类问题,我们使用分类器(classifier)来对合并后的训练集(X\_train)和测试集(X\_test)数据进行预测。通过
np.concatenate((X_train,X_test), axis=0)将训练集和测试集沿着轴 0 进行合并,然后使用分类器的predict方法得到预测结果,并将其存储在数据框(df)的prediction列中。 -
代码如下:
go# 创建整个数据集的预测 df\["prediction"\] = classifier.predict(np.concatenate((X\_train,X\_test), axis=0)) -
接着,将预测结果中的 0 值转换为 -1,1 值保持不变,通过
np.where实现这一转换,同样存储在prediction列中。 -
代码如下:
godf\["prediction"\] = np.where(df\["prediction"\] == 0, -1,1) -
最后,根据预测结果计算策略(strategy),即通过预测值的符号(
np.sign)乘以收益(returns)得到。 -
代码如下:
go# 计算策略 df\["strategy"\] = np.sign(df\["prediction"\]) * df\["returns"\]
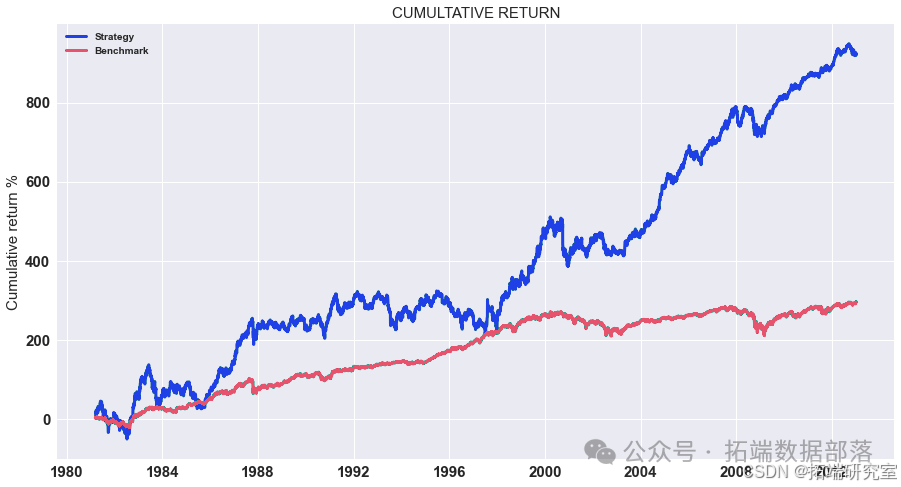
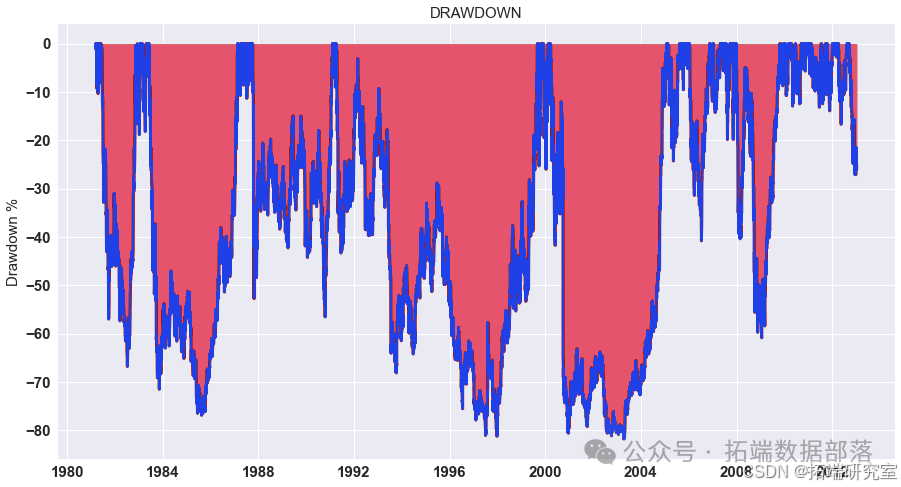
点击标题查阅往期内容

R语言时间序列:ARIMA / GARCH模型的交易策略在外汇市场预测应用

左右滑动查看更多

01
02
03
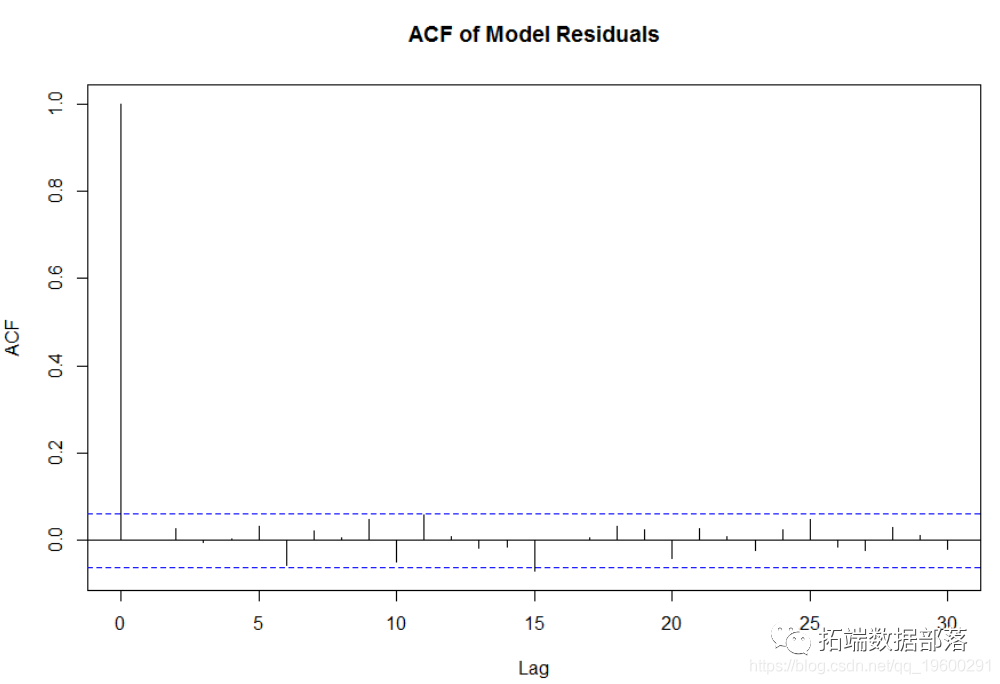
04
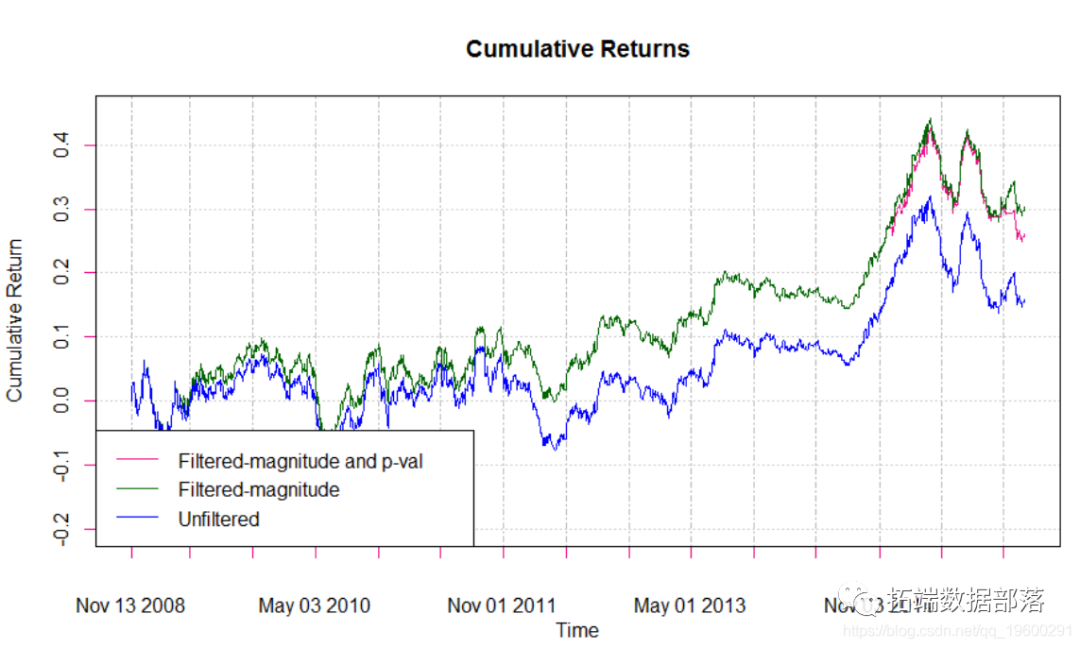
- 回归预测
-
对于回归任务,使用回归器(regressor)来进行预测。同样是对合并后的训练集和测试集数据进行操作,将预测结果存储在数据框的
prediction列中。 -
代码如下:
go# 创建整个数据集的预测 df\["prediction"\] = regressor.predict(np.concatenate((X\_train,X\_test), axis=0)) -
然后按照与分类预测中相同的方式计算策略。
-
代码如下:
go# 计算策略 df\["strategy"\] = np.sign(df\["prediction"\]) * df\["returns"\]
回测
- 分类回测
-
在分类任务中,对数据框中
strategy列的前split个数据进行动态投资组合的回测(backtest_dynamic_portfolio)。 -
代码如下:
go# 回测 backtest\_dynamic\_portfolio(df\["strategy"\].iloc\[:split\])
- 回归回测
-
在回归任务中,对数据框中
strategy列从split之后的数据进行动态投资组合的回测。 -
代码如下:
go# 回测 backtest\_dynamic\_portfolio(df\["strategy"\].iloc\[split:\])
深度神经网络(DNN)实现回归
- 自定义损失函数 ALPHA_MSE
-
定义了一个自定义的损失函数
ALPHA_MSE,它用于衡量预测值(y\_pred)和真实值(y\_true)之间的误差。在这个函数中,通过一些张量操作(如tf.roll进行数据的滚动,tf.math.sign获取符号,tf.where根据条件赋值等)来计算一个缩放的均方误差(scale_mse)。 -
代码如下:
godef ALPHA\_MSE(y\_true, y_pred): y\_true\_roll = tf.roll(y_true, shift=1, axis=0) y\_pred\_roll = tf.roll(y_pred, shift=1, axis=0) y\_true\_dif = tf.math.sign(y\_true\_roll - y_true) y\_pred\_dif = tf.math.sign(y\_pred\_roll - y_pred) booleen\_vector = y\_true\_dif == y\_pred_dif alpha = tf.where(booleen_vector, 1, 3) alpha = tf.cast(alpha, dtype=tf.float32) mse = F.square(y\_true - y\_pred) mse = tf.cast(mse, dtype=tf.float32) scale_mse = tf.multiply(alpha, mse) alpha\_mse = F.mean(scale\_mse) return alpha_mse
- 构建深度神经网络模型
-
导入必要的库(如
tensorflow、tensorflow_probability、tensorflow.keras.backend as F等)。 -
设定隐藏层数(
nb_hidden_layer = 3)。 -
初始化一个顺序模型(
Sequential)作为回归器(regressor)。 -
通过循环添加多个具有 75 个神经元、
relu激活函数的全连接层(Dense)和Dropout层。 -
再添加一个具有 1 个神经元、线性激活函数(
linear)的全连接层。 -
编译模型,指定损失函数为自定义的
ALPHA_MSE,优化器为adam。 -
训练模型,使用缩放后的训练数据(
X_train_scaled)和训练目标(y_train_reg),设置训练轮数(epochs = 13)、批大小(batch_size = 32)等参数。 -
代码如下:
goimport tensorflow from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, Dropout nb\_hidden\_layer = 3 np.random.seed(15) # 初始化顺序模型 regressor = Sequential() # 添加密集层和丢弃层 for _ in range(nb\_hidden\_layer): regressor.add(Dense(75, input\_shape = (X\_train.shape\[1\],), activation="relu")) # 添加密集层 regressor.add(Dense(1, activation="linear")) # 编译模型 regressor.compile(loss=ALPHA_MSE, optimizer="adam") regressor.fit(X\_train\_scaled, y\_train\_reg, epochs=13, batch_size=32, verbose=1)
- 进行预测和回测
-
与前面回归预测和回测的步骤相同,使用训练好的回归器对合并后的数据集进行预测,计算策略,并对策略进行回测。
-
代码如下:
go# 创建整个数据集的预测 df\["prediction"\] = regressor.predict(np.concatenate((X\_train,X\_test), axis=0)) # 计算策略 df\["strategy"\] = np.sign(df\["prediction"\]) * df\["returns"\] # 回测 from Backtest import * backtest\_dynamic\_portfolio(df\["strategy"\].iloc\[split:\])
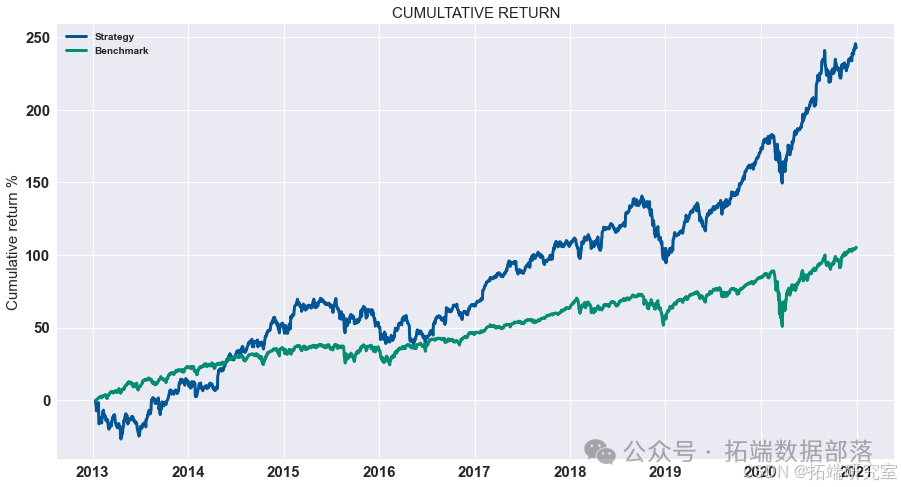
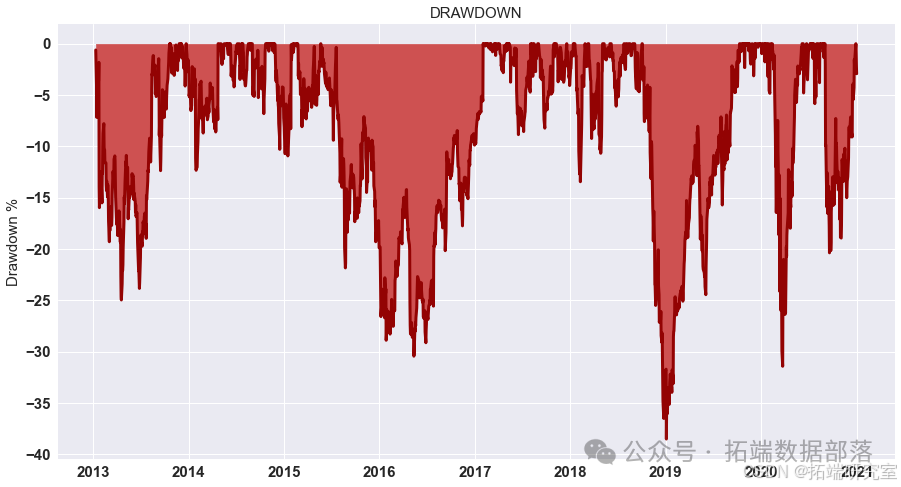
循环神经网络(RNN)
一、将二维数据转换为三维数据
在循环神经网络的应用中,常常需要将二维数据转换为三维数据。以下是一个实现此功能的函数X_3d_RNN:
- 数据验证
-
首先进行简单的数据验证,检查输入特征数据
X_s的长度和目标数据y_s的长度是否相等。如果不相等,则打印警告信息。 -
代码如下:
go# 简单验证 if len(X\_s)!= len(y\_s): print("Warnings")
- 创建三维的训练特征数据(X_train)
-
对于每个特征变量(通过
range(0, X_s.shape[1])遍历),创建一个新的列表X。 -
对于每个时间步(通过
range(lag, X_s.shape[0])遍历,其中lag是一个给定的时间滞后参数),从原始特征数据X_s中提取从i - lag到i的切片,并将其添加到X中。 -
将所有特征变量对应的
X组合成X_train,并进行轴的交换(np.swapaxes)以得到合适的三维数据结构。 -
代码如下:
go# 创建 X_train X_train = \[\] for variable in range(0, X_s.shape\[1\]): X = \[\] for i in range(lag, X_s.shape\[0\]): X.append(X_s\[i - lag:i, variable\]) X_train.append(X) X\_train = np.array(X\_train) X\_train = np.swapaxes(np.swapaxes(X\_train, 0, 1), 1, 2)
- 创建训练目标数据(y_train)
-
对于目标数据
y_s,从lag开始(因为前面的时间步可能用于构建序列信息),将每个时间步的数据进行重塑(reshape(-1, 1))和转置(transpose),并添加到y_train列表中。 -
最后,将
y_train列表中的所有数据沿轴 0 进行拼接(np.concatenate)。 -
代码如下:
go# 创建 y_train y_train = \[\] for i in range(lag, y_s.shape\[0\]): y\_train.append(y\_s\[i, :\].reshape(-1, 1).transpose()) y\_train = np.concatenate(y\_train, axis=0) -
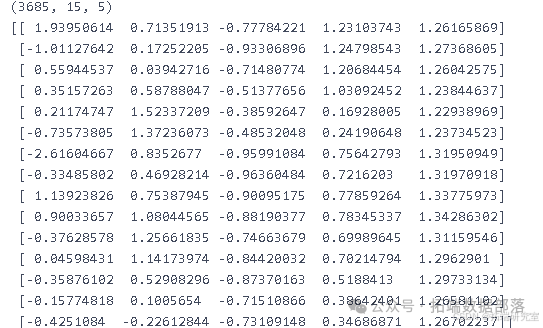
例如,给定一个滞后值
lag = 15,对经过缩放的训练特征数据X_train_scaled和分类目标数据y_train_cla.values以及测试特征数据X_test_scaled和测试分类目标数据y_test_cla.values进行转换,得到三维的训练特征数据X_train_3d、训练目标数据y_train_3d、测试特征数据X_test_3d和测试目标数据y_test_3d。 -
代码如下:
golag = 15 X\_train\_3d, y\_train\_3d = X\_3d\_RNN(X\_train\_scaled, y\_train\_cla.values, 15) X\_test\_3d, y\_test\_3d = X\_3d\_RNN(X\_test\_scaled, y\_test\_cla.values, 15) -
可以打印出转换后的训练特征数据的形状(
np.shape(X_train_3d))和第一个数据点(X_train_3d[0])来查看数据的结构。
预测和回测
- 分类问题的预测和数据整理
-
对于分类问题,创建整个数据集的预测。首先,在预测结果前添加
lag个零值(np.zeros([lag, 1])),然后与分类器(classifier)对三维训练特征数据X_train_3d和测试特征数据X_test_3d的预测结果进行拼接(np.concatenate),并将其存储在数据框(df)的prediction列中。 -
代码如下:
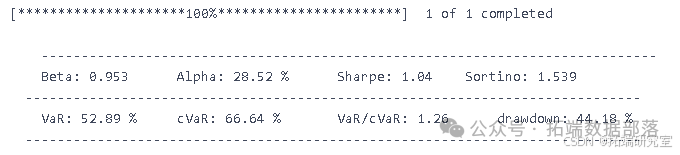
go# 创建整个数据集的预测 y\_pred\_train = np.concatenate((np.zeros(\[lag, 1\]), classifier.predict(X\_train\_3d)), axis=0) y\_pred\_test = np.concatenate((np.zeros(\[lag, 1\]), classifier.predict(X\_test\_3d)), axis=0) df\["prediction"\] = np.concatenate((y\_pred\_train, y\_pred\_test), axis=0)
- 回归问题的预测和数据整理
-
对于回归问题,首先对回归器(regressor)对三维训练特征数据
X_train_3d的预测结果进行逆变换(sc_y.inverse_transform),得到原始数据尺度下的预测值y_train_sc。 -
然后在预测结果前添加
lag个零值,并进行拼接。 -
代码如下:
go# 逆变换 y\_train\_sc = sc\_y.inverse\_transform(regressor.predict(X\_train\_3d)) # 预测 y\_pred\_train = np.concatenate((np.zeros(\[lag, 1\]), y\_train\_sc), axis=0)
通过上述步骤,实现了二维数据到三维数据的转换,以及基于转换后数据的分类和回归问题的预测准备工作。这些步骤为在循环神经网络中进行后续的模型训练、评估和分析奠定了基础。
请注意,上述代码中的X_train_scaled、y_train_cla、X_test_scaled、y_test_cla、classifier、regressor和sc_y等变量需要根据实际情况进行定义和导入。
go
# Create predictions for the whole dataset# Inverse transformy\_train\_sc = sc\_y.inverse\_transform(regressor.predict(X\_train\_3d))# Predictionsy\_pred\_train = np.concatenate((np.zeros(\[lag,1\]),y\_train\_sc),axis=0)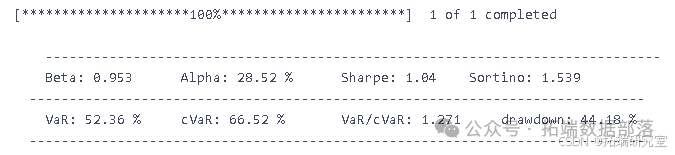
循环卷积神经网络(RCNN)
一、创建一个 RCNN
以下是一个用于创建循环卷积神经网络(RCNN)的函数RCNN:
- 库的导入和模型初始化
-
首先,导入必要的库,包括
tensorflow、tensorflow.keras.models中的Sequential以及tensorflow.keras.layers中的Conv1D、Dense、LSTM和Dropout。 -
代码如下:
go# 库的导入 import tensorflow from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Conv1D, Dense, LSTM, Dropout -
然后,初始化一个顺序模型(Sequential),这是构建神经网络模型的基础结构。
-
代码如下:
go# 模型初始化 model = Sequential()
- 添加 LSTM 层
-
向模型中添加一个长短期记忆(LSTM)层。
units参数指定了该层中神经元的数量(由输入参数number_neurons给定),return_sequences = True表示输出序列的最后一个输出将作为下一层的输入,input_shape参数指定了输入数据的形状(由输入参数shape给定)。 -
代码如下:
go# 添加 LSTM 层 model.add(LSTM(units = number\_neurons, return\_sequences = True, input_shape = shape))
- 添加 Dropout 层
-
通常在神经网络中,为了防止过拟合,会添加 Dropout 层。Dropout 层会在训练过程中随机地将神经元的输出设置为 0,从而强制模型学习更鲁棒的特征。虽然代码中给出了添加 Dropout 层的注释,但具体实现还未给出。一般来说,添加 Dropout 层的代码如下(假设
pct_dropout为要设置的丢弃率):gomodel.add(Dropout(rate = pct_dropout))
在构建 RCNN 模型时,除了上述已展示的部分,还可以继续添加其他类型的层(如卷积层 Conv1D、全连接层 Dense 等),并根据具体的任务(如回归或分类)选择合适的损失函数(loss)、评估指标(metrics)、激活函数(activation)和优化器(optimizer)。这些参数都可以作为函数的输入进行灵活配置。
决策树、SVM、回归机器学习方法金融交易策略
一、数据导入
- 初始化设备与创建空列表
-
首先初始化
mt5设备(mt5.initialize()),然后创建三个空列表:symbols用于存储交易品种符号,sectors用于存储交易品种所属板块,descriptions用于存储交易品种描述。 -
代码如下:
go# 初始化设备 mt5.initialize() # 创建空列表 symbols = \[\] sectors = \[\] descriptions = \[\]
- 获取交易品种信息并提取相关数据
-
通过
mt5.symbols_get()获取所有交易品种的信息,将其转换为列表形式(symbols_information_list)。 -
然后从列表中的每个元素提取交易品种符号、所属板块和描述信息,并分别添加到对应的列表中。
-
代码如下:
go# 获取所有交易品种信息 symbols\_information = mt5.symbols\_get() # 将元组转换为列表 symbols\_information\_list = list(symbols_information) # 提取交易品种符号、所属板块和描述信息 for element in symbols\_information\_list: symbols.append(list(element)\[-3\]) sectors.append(list(element)\[-1\].split("\\\")\[0\]) descriptions.append(list(element)\[-7\])
- 创建数据框并计算价差
-
根据提取的信息创建一个数据框(
informations)。 -
计算每个交易品种的价差(
spread),将其添加到数据框中,并筛选出价差小于0.0035的交易品种(lowest_spread_asset)。 -
代码如下:
go# 创建数据框 informations = pd.DataFrame(\[symbols, sectors, descriptions\], index=\["Symbol", "Sector", "Description"\]).transpose() # 创建空列表用于存储价差 spread = \[\] # 计算价差 for symbol in informations\["Symbol"\]: try: ask = mt5.symbol\_info\_tick(symbol).ask bid = mt5.symbol\_info\_tick(symbol).bid spread.append((ask - bid) / bid ) except: spread.append(None) # 将价差添加到数据框并筛选 informations\["Spread"\] = spread lowest\_spread\_asset = informations.dropna().loc\[informations\["Spread"\]<0.0035\]
- 定义获取数据的函数
-
定义一个函数
get_data,用于获取指定交易品种(symbol)、数量(n)和时间框架(timeframe)的数据。在函数内部,初始化mt5设备,将获取的数据放入数据框(rates_frame),并将时间列转换为日期时间格式。 -
代码如下:
godef get\_data(symbol, n, timeframe=mt5.TIMEFRAME\_D1): """ 函数用于返回交易品种的数据 """ # 初始化 MetaTrader 设备 mt5.initialize() # 将数据放入数据框 utc_from = datetime.now()+timedelta(hours=2) rates = mt5.copy\_rates\_from(symbol, timeframe, utc_from,n) rates_frame = pd.DataFrame(rates) # 将时间(单位:秒)转换为日期时间格式 rates\_frame\['time'\]=pd.to\_datetime(rates_frame\['time'\], unit='s') rates\_frame\['time'\] = pd.to\_datetime(rates_frame\['time'\], format='%Y-%m-%d') rates\_frame = rates\_frame.set_index('time') return rates_frame
二、特征工程
- 定义特征工程函数
-
定义函数
features_engineering,在函数内部,定义了一些全局变量(如X_train、X_test等)用于存储后续划分的数据集。 -
代码如下:
godef features_engineering(df): """ 此函数创建算法所需的所有数据集 """ # 使变量可在函数外部调用 global X_train global X_test global y\_train\_reg global y\_train\_cla global X\_train\_scaled global X\_test\_scaled global split\_train\_test global split\_test\_valid global X_valid global X\_valid\_scaled global X\_train\_pca global X\_test\_pca global X\_val\_pca
- 创建自定义指标和特征
-
创建了一些自定义指标(如
returns、sLow、sHigh)来计算策略收益,并进行特征工程(如returns t - 1、不同窗口的mean returns和volatility returns)。 -
代码如下:
go# 创建自定义指标来计算策略收益 df\["returns"\] = ((df\["close"\] - df\["close"\].shift(1)) / df\["close"\]) df\["sLow"\] = ((df\["low"\] - df\["close"\].shift(1)) / df\["close"\].shift(1)) df\["sHigh"\] = ((df\["high"\] - df\["close"\].shift(1)) / df\["close"\].shift(1)) # 特征工程 df\["returns t - 1"\] = df\[\["returns"\]\].shift(1) # 平均收益 df\["mean returns 15"\] = df\[\["returns"\]\].rolling(15).mean().shift(1) df\["mean returns 60"\] = df\[\["returns"\]\].rolling(60).mean().shift(1) # 收益波动率 df\["volatility returns 15"\] = df\[\["returns"\]\].rolling(15).std().shift(1) df\["volatility returns 60"\] = df\[\["returns"\]\].rolling(60).std().shift(1)
- 数据预处理
-
丢弃含有缺失值的数据,计算训练集、测试集和验证集的划分点,并创建训练集、测试集和验证集(
X_train、X_test、X_val)。 -
代码如下:
go# 丢弃缺失值 df = df.dropna() # 计算训练集划分点 split = int(0.80*len(df)) list_x = \["returns t - 1", "mean returns 15", "mean returns 60", "volatility returns 15", "volatility returns 60"\] split\_train\_test = int(0.70*len(df)) split\_test\_valid = int(0.90*len(df)) # 创建训练集 X\_train = df\[list\_x\].iloc\[:split\_train\_test\] y\_train\_reg = df\[\["returns"\]\].iloc\[:split\_train\_test\] y\_train\_cla = np.round(df\[\["returns"\]\].iloc\[:split\_train\_test\]+0.5) # 创建测试集 X\_test = df\[list\_x\].iloc\[split\_train\_test:split\_test\_valid\] # 创建验证集 X\_val = df\[list\_x\].iloc\[split\_test\_valid:\]
- 数据标准化和主成分分析(PCA)
-
导入
StandardScaler类对数据进行标准化处理,得到标准化后的训练集、测试集和验证集(X_train_scaled、X_test_scaled、X_val_scaled)。 -
导入
PCA类对标准化后的数据进行主成分分析,得到降维后的训练集、测试集和验证集(X_train_pca、X_test_pca、X_val_pca)。 -
代码如下:
go# 标准化 from sklearn.preprocessing import StandardScaler # 初始化标准化类 sc = StandardScaler() # 对数据进行标准化 X\_train\_scaled = sc.fit\_transform(X\_train) X\_test\_scaled = sc.transform(X_test) X\_val\_scaled = sc.transform(X_val) # PCA from sklearn.decomposition import PCA # 初始化 PCA 类 pca = PCA(n_components=3) # 应用 PCA X\_train\_pca = pca.fit\_transform(X\_train_scaled) X\_test\_pca = pca.transform(X\_test\_scaled) X\_val\_pca = pca.transform(X\_val\_scaled)
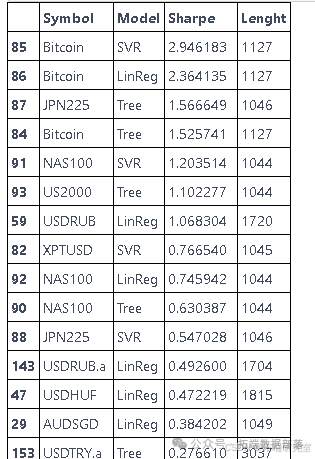
寻找最佳资产
- 定义预测函数
-
定义函数
predictor,用于对给定的数据(df)和模型(model)进行预测,并根据模型类型(reg)计算夏普比率。 -
代码如下:
godef predictor(df, model, reg=True, spread = 0.035): model.fit(X\_train\_pca, y\_train\_cla) df = df.dropna() # 为整个数据集创建预测 df\["prediction"\] = model.predict(np.concatenate((X\_train\_pca,X\_test\_pca, X\_val\_pca), axis=0)) if reg==False: df\["prediction"\] = np.where(df\["prediction"\]==0, -1, 1) df\["prediction"\] = df.prediction df=df.dropna() # 计算策略 df\["strategy"\] = df\["prediction"\]* df\["returns"\] returns = df\["strategy"\].iloc\[split\_train\_test:split\_test\_valid\] return np.sqrt(252) * (returns.mean()-(spread/100))/ returns.std()
- 导入模型并进行循环预测
-
导入一些机器学习模型(如
SVC、DecisionTreeClassifier、LogisticRegression),并对每个交易品种进行数据获取、特征工程和模型预测,将结果存储在列表中。 -
代码如下:
gofrom sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.linear_model import LogisticRegression from tqdm import tqdm # 模型 tree = DecisionTreeClassifier(max_depth=6) svr = SVC(C=1.5) lin = LogisticRegression() # 初始化 symbols = lowest\_spread\_asset\["Symbol"\] lists = \[\] lenght = \[\] mt5.initialize() for symbol in tqdm(symbols): try: df = get_data(symbol, 3500).dropna() df\["returns"\] = (df\["close"\] - df\["close"\].shift(1)) / df\["close"\].shift(1) features_engineering(df) """ 决策树回归器 """ sharpe_tree = predictor(df, tree, reg=True) lists.append(\[symbol, "Tree", sharpe_tree, len(df)\]) """ SVR """ sharpe_svr = predictor(df, svr, reg=False) lists.append(\[symbol, "SVR", sharpe_svr, len(df)\]) """ 线性回归 """ sharpe_linreg = predictor(df, lin, reg=False) lists.append(\[symbol, "LinReg", sharpe_linreg, len(df)\]) except: print("数据导入过程中出现问题")
四、组合算法
- 定义投票函数
-
定义函数
voting,用于创建基于投票方法的策略。在函数内部,根据reg参数选择不同的模型(分类或回归),进行训练、预测和策略计算。 -
代码如下:
godef voting(df, reg=True): """ 创建一个使用投票方法的策略 """ # 导入类 # 导入模型 if reg: tree = DecisionTreeRegressor(max_depth=6) svr = SVR(epsilon=1.5) lin = LinearRegression() vot = VotingRegressor(estimators=\[ ('lr', lin), ("tree", tree), ("svr", svr)\]) else: tree = DecisionTreeClassifier(max_depth=6) svr = SVC() lin = LogisticRegression() vot = VotingClassifier(estimators=\[ ('lr', lin), ("tree", tree), ("svr", svr)\]) # 训练模型 if reg==False: vot.fit(X\_train\_pca, y\_train\_cla) else: vot.fit(X\_train\_pca, y\_train\_reg) # 删除缺失值 df = df.dropna() # 为整个数据集创建预测 df\["prediction"\] = vot.predict(np.concatenate((X\_train\_pca, X\_test\_pca, X\_val\_pca), axis=0)) # 删除缺失值 df = df.dropna() if reg==False: df\["prediction"\] = np.where(df\["prediction"\]==0, -1, 1) # 计算策略 df\["strategy"\] = np.sign(df\["prediction"\]) * df\["returns"\] df\["low_strategy"\] = np.where(df\["prediction"\]>0, df\["sLow"\], -df\["sHigh"\]) df\["high_strategy"\] = np.where(df\["prediction"\]>0, df\["sHigh"\], -df\["sLow"\]) return vot, df\["strategy"\], df\["low\_strategy"\], df\["high\_strategy"\]
- 对多个资产进行操作
-
对多个资产(如
US2000、Bitcoin等)进行数据获取、特征工程、策略计算,并保存模型。 -
代码如下:
gomt5.initialize() # 导入类 from sklearn.svm import SVR, SVC from sklearn.tree import DecisionTreeRegressor, DecisionTreeClassifier from sklearn.linear_model import LinearRegression, LogisticRegression from sklearn.ensemble import VotingRegressor, VotingClassifier import pickle from joblib import dump, load # 初始化 lists = \[\] res = pd.DataFrame() low_assets = pd.DataFrame() high_assets = pd.DataFrame() for symbol in \["US2000", "Bitcoin", "JPN225", "XPTUSD", "NAS100"\]: print(symbol) # 导入数据 df = get_data(symbol, 3500).dropna() # 创建自定义指标来计算策略收益 df\["returns"\] = ((df\["close"\] - df\["close"\].shift(1)) / df\["close"\]) df\["sLow"\] = ((df\["low"\] - df\["close"\].shift(1)) / df\["close"\].shift(1)) df\["sHigh"\] = ((df\["high"\] - df\["close"\].shift(1)) / df\["close"\].shift(1)) # 删除缺失值 df = df.dropna() # 创建数据集 features_engineering(df) # 计算策略 vot, res\[symbol\],low\_assets\[symbol\],high\_assets\[symbol\] = voting(df, reg=False) # 保存模型 s = pickle.dumps(vot) alg = pickle.loads(s) dump(alg,f"Models/{symbol}_voting.joblib")
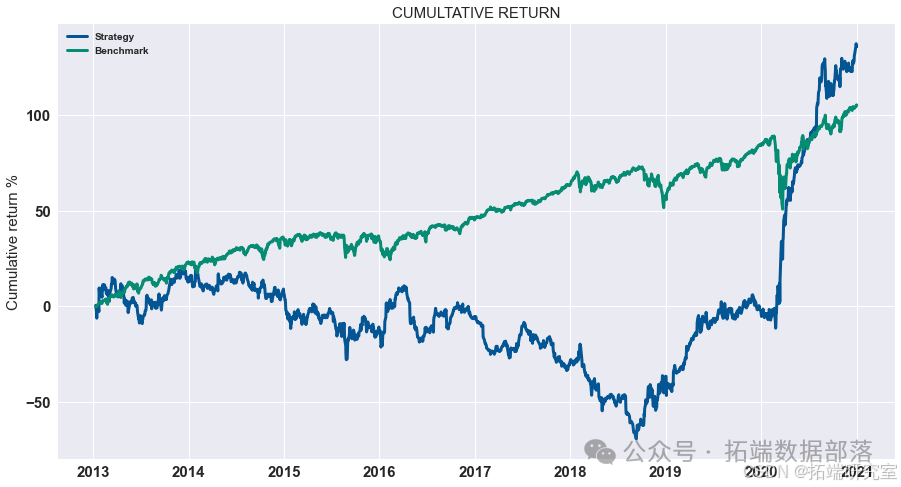
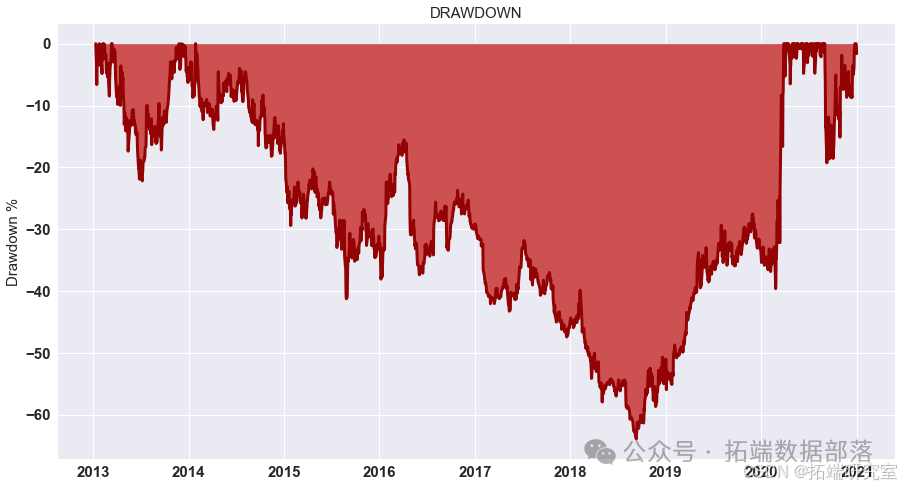
- 展示策略累积收益
-
对计算出的策略收益进行可视化展示,通过绘制累积收益图来观察策略在测试集上的表现。
-
代码如下:
go# 显示测试集上策略的累积收益 data = res.dropna().loc\["2020 - 01":"2021 - 01"\] data.cumsum().plot(figsize=(15,8))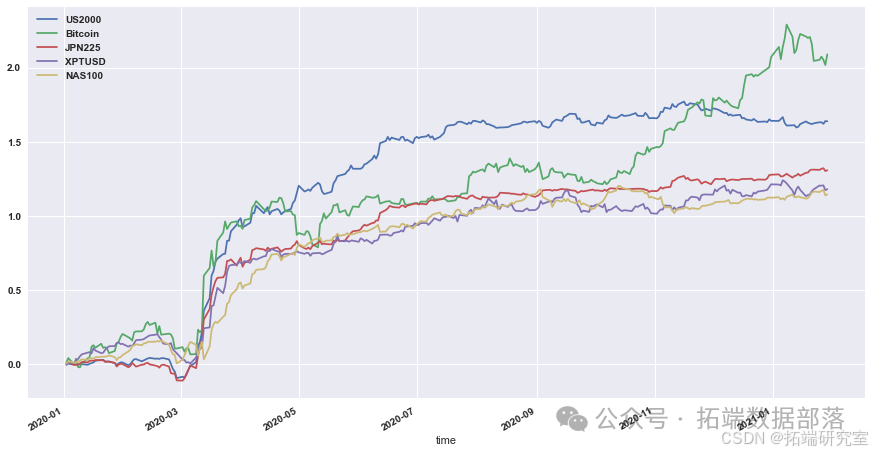

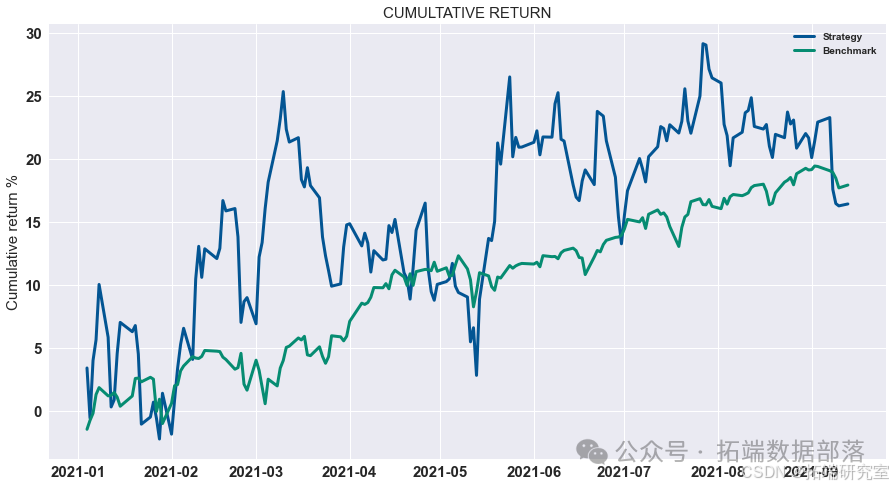
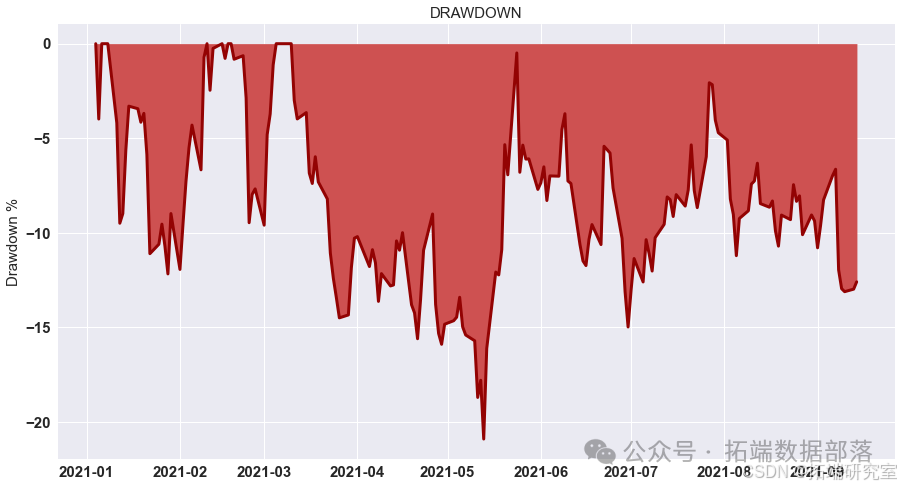
最优止盈、止损和杠杆
- 最优止盈
-
设定止盈比例(
tp),对投资组合数据(pf)进行处理,根据止盈条件调整收益值,然后进行动态投资组合回测。 -
代码如下:
gotp = 2.1/100 pf = pd.concat((low\_portfolio, portfolio\_return\_MV,high\_portfolio), axis=1).dropna()-spread pf.columns = \["low", "Return", "high"\] pf\["Return"\] = np.where(pf\["high"\].values>tp, tp, pf\["Return"\].values) pf\["Return"\] = np.where(pf\["Return"\].values>tp, tp, pf\["Return"\].values) backtest\_dynamic\_portfolio(pf\["Return"\])
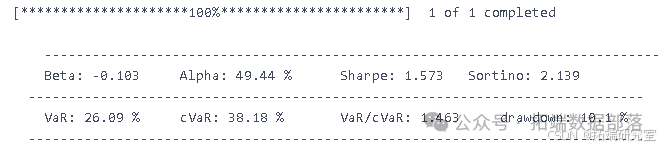
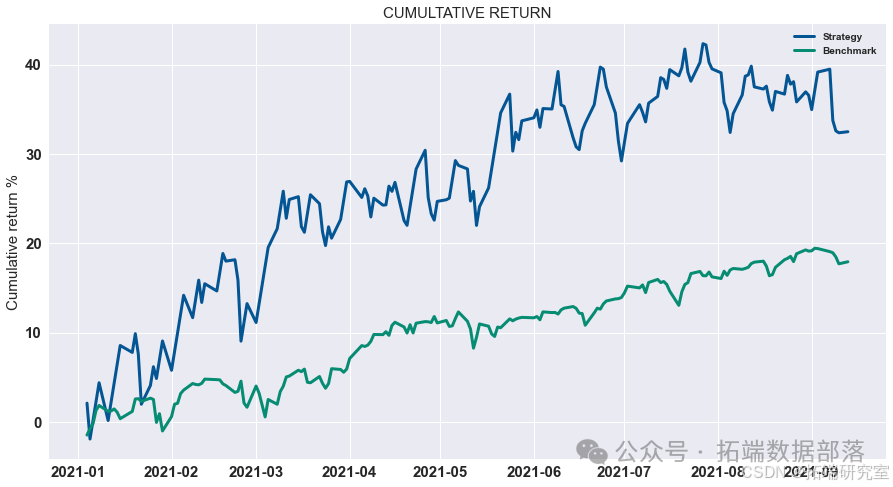
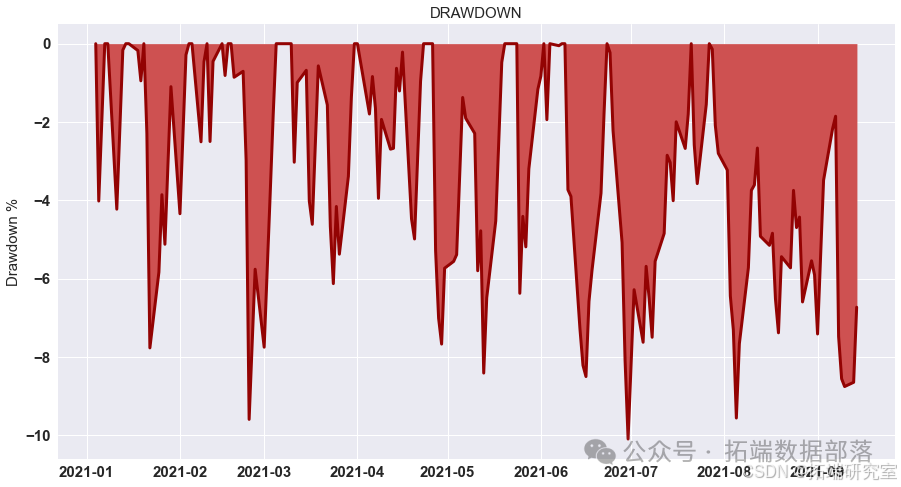
- 最优止损
-
定义函数
find_best_sl,用于寻找最佳止损比例(sl)。在函数内部,根据止损条件调整投资组合的收益值,并计算夏普比率。 -
代码如下:
go
def find\_best\_sl(sl):
sl = sl/100
# 创建投资组合
pf = pd.concat((low\_portfolio, portfolio\_return\_test,high\_portfolio), axis=1).dropna()-spread
pf.columns = \["low", "Return", "high"\]
# 应用止损
pf\["Return"\] = np.where(pf\["low"\].values<-sl, -sl, pf\["Return"\].values)
pf\["Return"\] = np.where(pf\["Return"\].values<-sl, -sl, pf\["Return"\].values)
# 返回夏普比率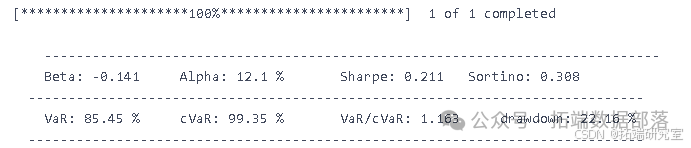
关于分析师

在此对 Aijun Zhang 对本文所作的贡献表示诚挚感谢,他完成了数据科学与大数据技术专业的学位。擅长 Python、深度学习、数据处理分析。

本文中分析的数据、代码**** 分享到会员群,扫描下面二维码即可加群!
资料获取
在公众号后台回复"领资料",可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末**"阅读原文"**
获取全文完整代码数据资料。
本文选自《深度神经网络DNN、RNN、RCNN及多种机器学习金融交易策略探索》。
点击标题查阅往期内容
matlab使用长短期记忆(LSTM)神经网络对序列数据进行分类
Python用MarkovRNN马尔可夫递归神经网络建模序列数据t-SNE可视化研究
视频:Python深度学习量化交易策略、股价预测:LSTM、GRU深度门控循环神经网络|附代码数据
R语言ARMA GARCH COPULA模型拟合股票收益率时间序列和模拟可视化
GJR-GARCH和GARCH波动率预测普尔指数时间序列和Mincer Zarnowitz回归、DM检验、JB检验
【视频】时间序列分析:ARIMA-ARCH / GARCH模型分析股票价格
PYTHON用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化
极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值:ARIMA,GARCH,Delta-normal法滚动估计VaR(Value at Risk)和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格




