文章目录
-
- 一、基本图像增强(数值运算)
-
- [1.1 加法 (cv2.add)](#1.1 加法 (cv2.add))
-
- [1.1.1 图像与标量相加(调节亮度)](#1.1.1 图像与标量相加(调节亮度))
- [1.1.2 图像与图像相加(两个图像shape要相同)](#1.1.2 图像与图像相加(两个图像shape要相同))
- [1.1.3 图像的加权加法(渐变切换)](#1.1.3 图像的加权加法(渐变切换))
- [1.2 乘法/对比度(cv2.multiply)](#1.2 乘法/对比度(cv2.multiply))
- [1.3 使用np.clip处理溢出](#1.3 使用np.clip处理溢出)
- [1.4 阈值处理](#1.4 阈值处理)
- [1.5 位运算](#1.5 位运算)
- [1.6 图像的叠加:制作coca-cola彩色Logo](#1.6 图像的叠加:制作coca-cola彩色Logo)
- 二、滤波器(Filter)
-
- [2.1 简介](#2.1 简介)
-
- [2.1.1 滤波器原理](#2.1.1 滤波器原理)
- [2.1.2 卷积函数filter2D](#2.1.2 卷积函数filter2D)
- [2.1.3 滤波器分类](#2.1.3 滤波器分类)
- [2.2 降噪](#2.2 降噪)
-
- [2.2.1 方盒滤波器](#2.2.1 方盒滤波器)
- [2.2.2 均值滤波器](#2.2.2 均值滤波器)
- [2.2.3 高斯滤波器](#2.2.3 高斯滤波器)
-
- [2.2.3.1 高斯函数](#2.2.3.1 高斯函数)
- [2.2.3.2 高斯滤波器](#2.2.3.2 高斯滤波器)
- [2.2.4 中值滤波器](#2.2.4 中值滤波器)
- [2.2.5 双边滤波器](#2.2.5 双边滤波器)
-
- [2.2.5.1 工作原理](#2.2.5.1 工作原理)
- [2.2.5.2 bilateralFilter](#2.2.5.2 bilateralFilter)
- [2.3 边缘检测](#2.3 边缘检测)
-
- [2.3.1 sobel算子](#2.3.1 sobel算子)
- [2.3.2 Scharr算子](#2.3.2 Scharr算子)
- [2.3.3 Laplacian算子](#2.3.3 Laplacian算子)
- [2.3.4 Canny](#2.3.4 Canny)
- [2.3.5 总结](#2.3.5 总结)
一、基本图像增强(数值运算)
图像处理技术利用数学运算获得不同的结果。通常,我们使用一些基本操作可以得到图像的简单增强。在本章中,我们将介绍:
- 算术运算,如加法、乘法
- 阈值和屏蔽(masking)
- 按位运算,如OR、AND、XOR
python
# Import libraries
import cv2
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
%matplotlib inline
from IPython.display import Image下面用opencv读取一张新西兰海岸照
python
img_bgr = cv2.imread("New_Zealand_Coast.jpg",cv2.IMREAD_COLOR)
img_rgb = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2RGB)
# Display 18x18 pixel image.
Image(filename='New_Zealand_Coast.jpg')
1.1 加法 (cv2.add)
函数 cv2.add()用于图像的加法运算,其语法为dst=cv2.add(src1, src2 [, dst[, mask[, dtype]])
scr1, scr2:进行加法运算的图像,或一张图像与一个 numpy array 标量mask:掩模图像,8位灰度格式;掩模图像数值为 0 的像素,输出图像对应像素的各通道值也为 0(被mask位置像素输出为0)。可选项,默认值为 None。dtype:图像数组的深度,即每个像素值的位数,可选项
需要注意的是,OpenCV 加法和 numpy 加法之间有区别:cv2.add() 是饱和运算(相加后如大于 255 则结果为 255),而 Numpy 加法是模运算。
1.1.1 图像与标量相加(调节亮度)
本节讨论图像加法的简单操作------图像与标量相加,这会导致图像亮度的增加或减少,因为我们最终会对每个像素值增加或减少相同的值。(亮度会全局地增加/减少)
python
matrix = np.ones(img_rgb.shape, dtype = "uint8") * 50
img_rgb_brighter = cv2.add(img_rgb, matrix)
img_rgb_darker = cv2.subtract(img_rgb, matrix)
# Show the images
plt.figure(figsize=[18,5])
plt.subplot(131); plt.imshow(img_rgb_darker); plt.title("Darker");
plt.subplot(132); plt.imshow(img_rgb); plt.title("Original");
plt.subplot(133); plt.imshow(img_rgb_brighter);plt.title("Brighter");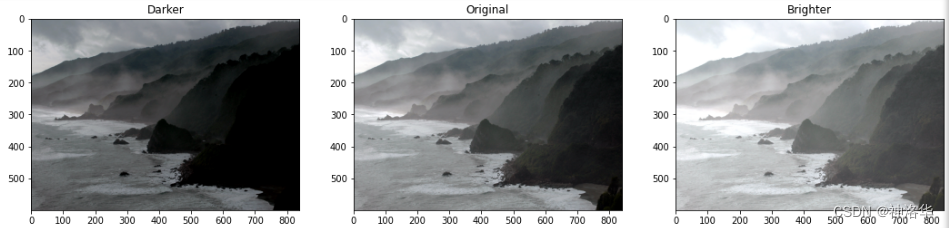
另外,图像也可以与常数相加。下面进行常数相加和标量相加的对比:
python
Value =70 # 常数
Scalar = np.ones((1, 3), dtype="float") * Value # 标量
imgAddV = cv2.add(img_bgr , Value) # OpenCV 加法: 图像 + 常数
imgAddS = cv2.add(img_bgr , Scalar) # OpenCV 加法: 图像 + 标量
print("Shape of scalar", Scalar)
for i in range(1, 6):
x, y = i*10, i*10
print("(x,y)={},{}, img_bgr:{}, imgAddV:{}, imgAddS:{}"
.format(x,y,img_bgr [x,y],imgAddV[x,y],imgAddS[x,y]))
python
# 打印图像中的6个点,可以看到相加后像素值的变化
Shape of scalar [[70. 70. 70.]]
(x,y)=10,10, img_bgr:[184 179 170], imgAddV:[254 179 170], imgAddS:[254 249 240]
(x,y)=20,20, img_bgr:[185 179 172], imgAddV:[255 179 172], imgAddS:[255 249 242]
(x,y)=30,30, img_bgr:[189 182 173], imgAddV:[255 182 173], imgAddS:[255 252 243]
(x,y)=40,40, img_bgr:[187 181 174], imgAddV:[255 181 174], imgAddS:[255 251 244]
(x,y)=50,50, img_bgr:[193 188 179], imgAddV:[255 188 179], imgAddS:[255 255 249]
python
plt.figure(figsize=[18,5])
plt.subplot(131), plt.title("1. img1"), plt.axis('off')
plt.imshow(cv2.cvtColor(img_bgr , cv2.COLOR_BGR2RGB)) # 显示 img_bgr(RGB)
plt.subplot(132), plt.title("2. img + constant"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddV, cv2.COLOR_BGR2RGB)) # 显示 imgAddV(RGB)
plt.subplot(133), plt.title("3. img + scalar"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddS, cv2.COLOR_BGR2RGB)) # 显示 imgAddS(RGB)
plt.show()
- 将图像与一个常数 value 相加,只是将 B 通道即蓝色分量与常数相加,而 G、R 通道的数值不变,因此图像发蓝。
- 将图像与一个标量 scalar 相加,"标量" 是指一个 1x3 的 numpy 数组,此时 B/G/R 通道分别与数组中对应的常数相加,因此图像发白。(数组中各元素可不相同)
1.1.2 图像与图像相加(两个图像shape要相同)
python
img1 = cv2.imread("../images/imgB1.jpg") # 读取彩色图像(BGR)
img2 = cv2.imread("../images/imgB3.jpg") # 读取彩色图像(BGR)
imgAddCV = cv2.add(img1, img2) # OpenCV 加法: 饱和运算
imgAddNP = img1 + img2 # Numpy 加法: 模运算
plt.subplot(221), plt.title("1. img1"), plt.axis('off')
plt.imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)) # 显示 img1(RGB)
plt.subplot(222), plt.title("2. img2"), plt.axis('off')
plt.imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)) # 显示 img2(RGB)
plt.subplot(223), plt.title("3. cv2.add(img1, img2)"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddCV, cv2.COLOR_BGR2RGB)) # 显示 imgAddCV(RGB)
plt.subplot(224), plt.title("4. img1 + img2"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddNP, cv2.COLOR_BGR2RGB)) # 显示 imgAddNP(RGB)
plt.show()
图 3 是 cv2.add() 饱和加法的结果,图 4 是 numpy 取模加法的结果。饱和加法以 255 为上限,所有像素只会变的更白(大于原值);取模加法以 255 为模,会导致部分像素变黑 (小于原值)。因此,一般情况下应使用 cv2.add 进行饱和加法操作,不宜使用 numpy 取模加法。
1.1.3 图像的加权加法(渐变切换)
函数 cv2.addWeight() 用于图像的加权加法运算,可以实现图像的叠加和混合。其语法为:
python
dst=cv2.addWeighted(src1, alpha, src2, beta, gamma[, dst[, dtype]]) 简单理解就是: d s t = s r c 1 ∗ a l p h a + s r c 2 ∗ b e t a + g a m m a dst = src1 * alpha + src2 * beta + gamma dst=src1∗alpha+src2∗beta+gamma,推荐取 beta=1-alpha, gamma=0。
alpha/beta:第一、二张图像 的权重,通常取为 0~1 之间的浮点数gamma: 灰度系数,图像校正的偏移量,用于调节亮度dtype:输出图像的深度,即每个像素值的位数,可选项,default=src1.depth()
python
img1 = cv2.imread("../images/imgGaia.tif") # 读取图像 imgGaia
img2 = cv2.imread("../images/imgLena.tif") # 读取图像 imgLena
imgAddW1 = cv2.addWeighted(img1, 0.2, img2, 0.8, 0) # 加权相加, a=0.2, b=0.8
imgAddW2 = cv2.addWeighted(img1, 0.5, img2, 0.5, 0) # 加权相加, a=0.5, b=0.5
imgAddW3 = cv2.addWeighted(img1, 0.8, img2, 0.2, 0) # 加权相加, a=0.8, b=0.2
plt.subplot(131), plt.title("1. a=0.2, b=0.8"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddW1, cv2.COLOR_BGR2RGB)) # 显示 img1(RGB)
plt.subplot(132), plt.title("2. a=0.5, b=0.5"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddW2, cv2.COLOR_BGR2RGB)) # 显示 imgAddV(RGB)
plt.subplot(133), plt.title("3. a=0.8, b=0.2"), plt.axis('off')
plt.imshow(cv2.cvtColor(imgAddW3, cv2.COLOR_BGR2RGB)) # 显示 imgAddS(RGB)
plt.show()
不同尺寸图像的相加,可先将二者调整到同一尺寸,方法见本章4.6节。
1.2 乘法/对比度(cv2.multiply)
对比度是图像像素值的差异,将像素值与常数相乘可以使差值变大或变小。
python
matrix1 = np.ones(img_rgb.shape) * 0.5
matrix2 = np.ones(img_rgb.shape) * 1.5
# 先将img_rgb转为浮点数类型进行乘法计算,计算完成后,我们再将结果转换回np.uint8类型
# 因为图像数据通常是以8位无符号整数形式存储的。
img_rgb_darker = np.uint8(cv2.multiply(np.float64(img_rgb), matrix1))
img_rgb_brighter = np.uint8(cv2.multiply(np.float64(img_rgb), matrix2))
# Show the images
plt.figure(figsize=[18,5])
plt.subplot(131); plt.imshow(img_rgb_darker); plt.title("Lower Contrast");
plt.subplot(132); plt.imshow(img_rgb); plt.title("Original");
plt.subplot(133); plt.imshow(img_rgb_brighter);plt.title("Higher Contrast");
右边图会发现图像的某些区域看到奇怪的颜色,这是因为相乘后某些像素值>255,已经溢出,这该如何处理呢?
1.3 使用np.clip处理溢出
np.clip函数用于裁剪数组中的元素,使其值位于指定的范围之内,其语法为:
python
np.clip(a, a_min, a_max)下面是一个简单的示例:
python
img_rgb_higher = np.uint8(np.clip(cv2.multiply(np.float64(img_rgb), matrix2),0,255))
# Show the images
plt.figure(figsize=[18,5])
plt.subplot(131); plt.imshow(img_rgb_lower); plt.title("Lower Contrast");
plt.subplot(132); plt.imshow(img_rgb); plt.title("Original");
plt.subplot(133); plt.imshow(img_rgb_higher);plt.title("Higher Contrast");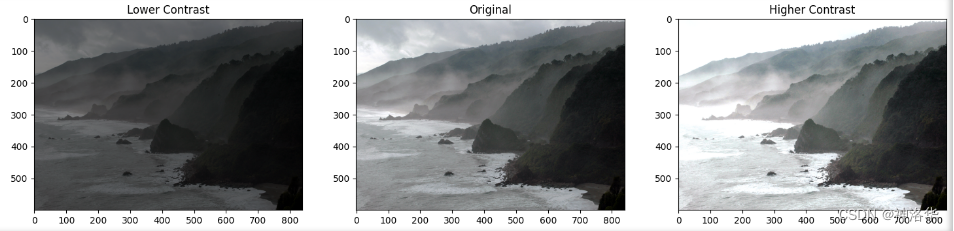
1.4 阈值处理
相见《OpenCV系列教程三:形态学、图像轮廓、直方图》
1.5 位运算
在OpenCV中,位运算通常指的是对图像的像素值进行位操作,即将每个十进制的像素值看作 8 位二进制数,按位对每一对像素值执行对应的位运算,最后将结果转换回十进制像素值。常见位运算包括:
-
cv2.bitwise_and: result ( i , j ) = src1 ( i , j ) & src2 ( i , j ) \text{result}(i, j) = \text{src1}(i, j) \, \& \, \text{src2}(i, j) result(i,j)=src1(i,j)&src2(i,j)- 按位 "与" 操作, 对应位都为1的情况下,结果为1,否则是 0。(黑色和任何颜色做与操作都是黑色,白色与任何颜色进行与操作的结果都是那个颜色,图像与自身做与操作,结果不变)
- 效果: 主要用于图像的区域掩码。例如,在图像中通过与一个掩码图像的与运算可以保留特定的区域,而其他地方为黑色。
-
bitwise_or: result ( i , j ) = src1 ( i , j ) ∣ src2 ( i , j ) \text{result}(i, j) = \text{src1}(i, j) \, | \, \text{src2}(i, j) result(i,j)=src1(i,j)∣src2(i,j)- 按位 "或" 操作,对应位只要有一个为1,结果就为1,否则为0。
- 效果: 将两个图像合并,重叠的部分会亮起,非重叠的部分也会被保留下来。
-
bitwise_xor: result ( i , j ) = src1 ( i , j ) ⊕ src2 ( i , j ) \text{result}(i, j) = \text{src1}(i, j) \, \oplus \, \text{src2}(i, j) result(i,j)=src1(i,j)⊕src2(i,j)- 按位 "异或" 操作,对应位不同为1,相同为0。
- 效果: 只保留两个图像中不同的部分,重叠的部分将变为黑色。
-
bitwise_not: result ( i , j ) = ¬ src ( i , j ) \text{result}(i, j) = \neg \text{src}(i, j) result(i,j)=¬src(i,j)- 按位 "非" 操作(即按位取反),所有的 0 变成 1,所有的 1 变成 0。
- 效果: 反转图像颜色,黑色变成白色,白色变成黑色。
以and位运算举例,其语法为:
python
cv2.bitwise_and(src1, src2, dst=None, mask=None)src1,src2: 这两个参数是要进行位运算的源图像。dst: 可选,存储位运算结果的图像。如果未指定,将创建一个与src1相同大小的图像。mask:可选,一个单通道的8位灰度图像(每个元素的值要么是0要么是255),用作掩码。当你提供了 mask,OpenCV 只会在 掩码中像素值为为 255(白色)的区域内对 src1 和 src2 进行按位 "与" 操作,mask为0的区域直接填充0。
也可以理解为
src1,src2先做与运算,再与mask做与运算。那么mask是白色的部分结果不变,黑色部分保留黑色(黑色和任何颜色与运算结果都是黑色)。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import Image
# 创建两个图像
img1=np.full((300, 300,3), 255, dtype=np.uint8)
img2 = np.full((300, 300,3), 255, dtype=np.uint8)
# 在img1上绘制一个白色矩形
cv2.rectangle(img1, (50, 50), (250, 250), (255, 0, 0), -1)
# 在img2上绘制一个白色圆
cv2.circle(img2, (150, 150), 100, (0, 0, 0), -1)
# 创建一个掩码(mask),掩码上绘制一个白色矩形
mask = np.zeros((300, 300), dtype=np.uint8)
cv2.rectangle(mask, (100, 100), (200, 200), 255, -1)
# 使用mask进行按位与操作
result= cv2.bitwise_and(img1, img2)
result_mask = cv2.bitwise_and(img1, img2, mask=mask)
# 显示图像
plt.subplot(131); plt.imshow(img1,cmap="gray"); plt.title("img1");
plt.subplot(132); plt.imshow(img2,cmap="gray"); plt.title("img2");
plt.subplot(133); plt.imshow(mask,cmap="gray"); plt.title("mask");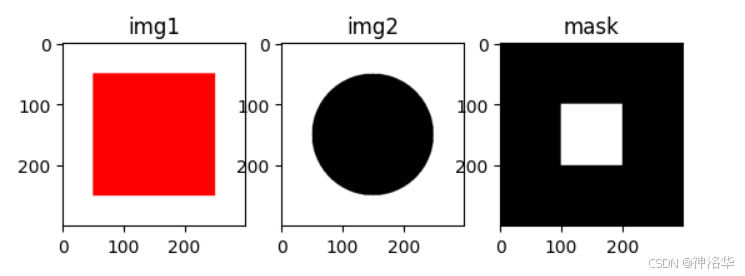
python
plt.subplot(121); plt.imshow(result,cmap="gray"); plt.title("result");
plt.subplot(122); plt.imshow(result_mask,cmap="gray"); plt.title("result_mask");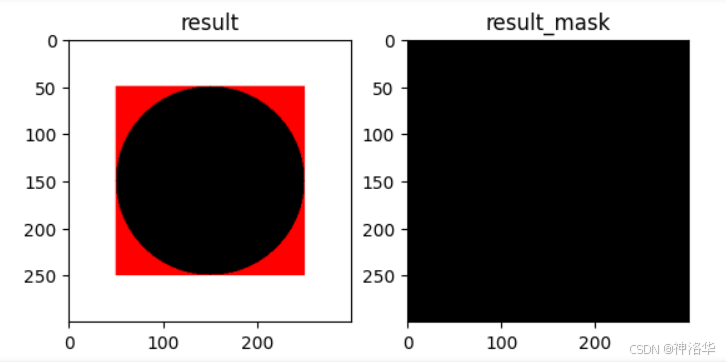
位运算应用场景
- 图像合并:通过 bitwise_and、bitwise_or 等操作,可以根据掩码合并图像的特定区域。
- 图像遮罩:通过位运算可以使用遮罩图像来选择性显示部分区域。
- 二值化操作:可以在处理二值图像时使用这些位运算进行更复杂的图像处理。
- 背景去除:通过掩码和位运算,能将背景移除,只保留感兴趣的前景区域。
下面举例说明,先正常读取一张矩形图和一张圆形图:
python
img_rec = cv2.imread("rectangle.jpg", 0)
img_cir = cv2.imread("circle.jpg", 0)
plt.figure(figsize=[20,5])
plt.subplot(121);plt.imshow(img_rec,cmap='gray')
plt.subplot(122);plt.imshow(img_cir,cmap='gray')
print(img_rec.shape,img_cir.shape)
python
(200, 499) (200, 499)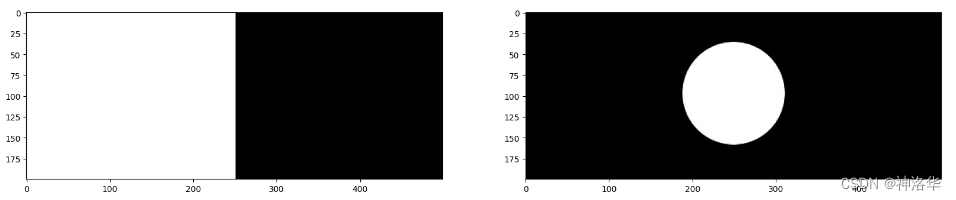
下面依次进行and、or、xor、not操作
python
img_and = cv2.bitwise_and(img_rec, img_cir, mask = None) # 与操作中一方是黑就显示黑
img_or= cv2.bitwise_or(img_rec, img_cir, mask = None) # 或操作中一方是白就显示白
img_xor= cv2.bitwise_xor(img_rec, img_cir, mask = None)
img_not=cv2.bitwise_not(img_rec, img_cir, mask = None)
#plt.imshow(result,cmap='gray')
plt.figure(figsize=[10,5])
plt.subplot(221); plt.imshow(img_and,cmap="gray"); plt.title("AND");
plt.subplot(222); plt.imshow(img_or,cmap="gray"); plt.title("OR");
plt.subplot(223); plt.imshow(img_xor,cmap="gray"); plt.title("XOR");
plt.subplot(224); plt.imshow(img_not,cmap="gray"); plt.title("NOT");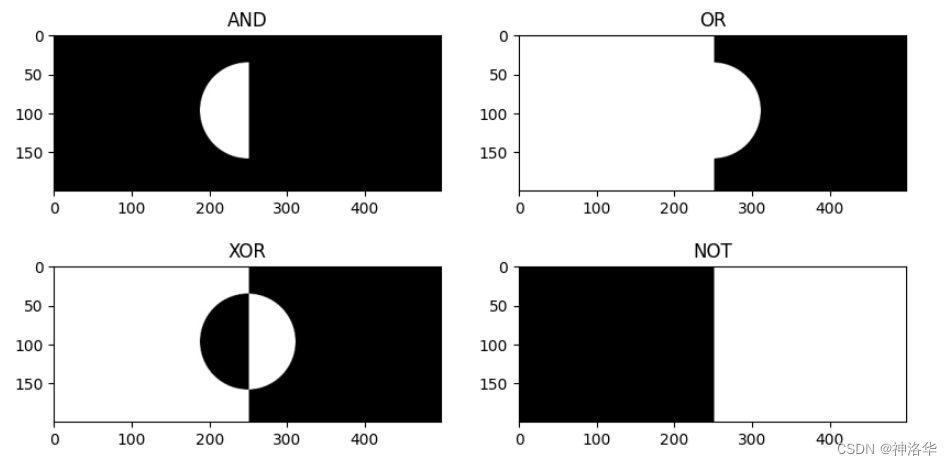
1.6 图像的叠加:制作coca-cola彩色Logo
两张图像直接进行加法运算后图像的颜色会改变,通过加权加法实现图像混合后图像的透明度会改变,都不能实现图像的叠加。
实现图像的叠加,需要综合运用图像阈值处理、图像掩模、位操作和图像加法的操作。下面展示如何用背景图像填充可口可乐Logo的白色字母。
python
Image(filename='Logo_Manipulation.png')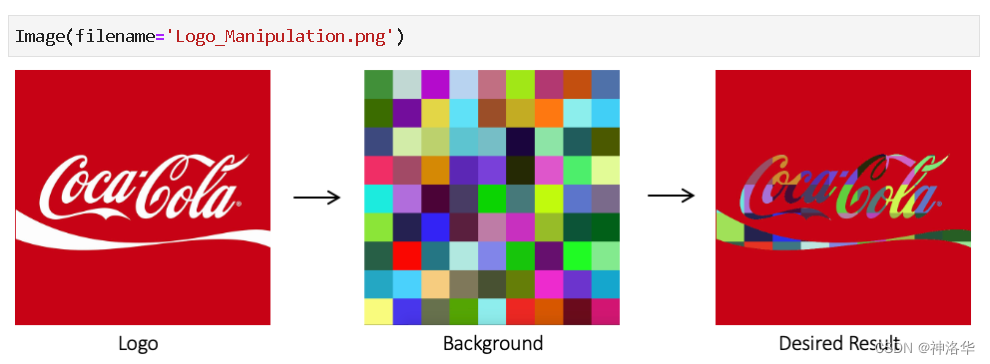
- 读取logo图片和背景图片,调整后者尺寸使二者尺寸相同
- 对前景图片(logo)进行二值化处理,生成黑白掩模图像 mask及其反转掩模图像 mask_Inv
- 以黑白掩模 mask作为掩模,对背景图像进行位操作,得到叠加背景图片Add_Background(只得到彩色logo)
- 以反转掩模 mask_Inv作为掩模,对前景图像进行位操作,得到叠加前景图像Foreground;(只得到除logo之外的区域)
- 二者通过 cv2.add 加法运算,得到叠加图像
1.读取Logo图片
python
img_bgr = cv2.imread("coca-cola-logo.png")
img_rgb = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2RGB)
logo_w,logo_h = img_rgb.shape[0],img_rgb.shape[1]
print(img_rgb.shape)
python
(700, 700, 3)- 读取背景图片
python
img_background_bgr = cv2.imread("checkerboard_color.png")
img_background_rgb = cv2.cvtColor(img_background_bgr, cv2.COLOR_BGR2RGB)
# 调整图片宽度,并保持高宽比不变
aspect_ratio = logo_w / img_background_rgb.shape[1]
dim = (logo_w, int(img_background_rgb.shape[0] * aspect_ratio))
# 背景图resize到和Logo一样大小
img_background_rgb = cv2.resize(img_background_rgb, dim, interpolation=cv2.INTER_AREA)
print(img_background_rgb.shape)
python
(700, 700, 3)- 创建掩码mask
python
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_RGB2GRAY) # RGB转灰度图
# 使用全局阈值创建Logo二值mask
retval, img_mask = cv2.threshold(img_gray,127,255,cv2.THRESH_BINARY)
print(img_mask.shape)- 反转mask
python
img_mask_inv = cv2.bitwise_not(img_mask)
python
plt.figure(figsize=[8,8])
plt.subplot(221); plt.imshow(img_rgb); plt.title("RGB");
plt.subplot(222); plt.imshow(img_background_rgb); plt.title("Background");
plt.subplot(223); plt.imshow(img_mask,cmap="gray"); plt.title("Mask");
plt.subplot(224); plt.imshow(img_mask_inv,cmap="gray"); plt.title("Mask_inv");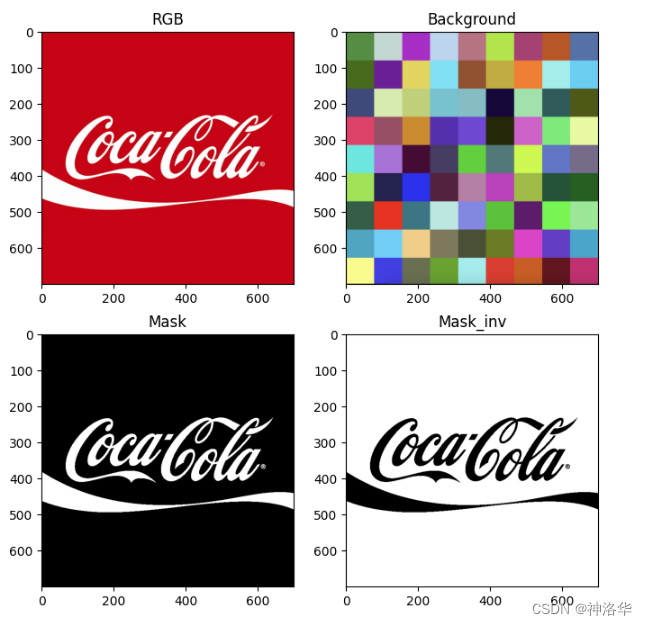
- mask图像加上背景
python
# 在logo字母上加上彩色背景
img_background = cv2.bitwise_and(img_background_rgb, img_background_rgb, mask=img_mask)
plt.imshow(img_background)- 将前景与图像分开
python
# img_mask_inv白色部分红
img_foreground = cv2.bitwise_and(img_rgb, img_rgb, mask=img_mask_inv)
plt.imshow(img_foreground)- 前景与背景相加得到最终结果
python
result = cv2.add(img_background,img_foreground)
plt.imshow(result)
cv2.imwrite("logo_final.png", result[:,:,::-1])
python
plt.figure(figsize=[15,5])
plt.subplot(141); plt.imshow(img_background); plt.title("Add_Background");
plt.subplot(142); plt.imshow(img_foreground); plt.title("Foreground");
plt.subplot(143); plt.imshow(result,cmap="gray"); plt.title("Result");
二、滤波器(Filter)
2.1 简介
2.1.1 滤波器原理
在 OpenCV 中,滤波器 是一种对图像进行处理的工具。通过对图像进行卷积操作,来增强图像的某些特征或去除噪声(平滑、锐化、去噪等)。滤波器的原理主要是通过一个卷积核 (kernel)对图像进行卷积,从而改变图像像素值。

滤波器 可以直接理解为卷积神经网络(CNN)中的卷积核(kernel),两者在核心原理上是相同的,都是通过卷积操作来处理图像信息,提取特征,但它们的使用方式和目的有所不同:
Filter:传统滤波器的参数是预定义的,专应用于特定任务。如图像处理中的去噪、平滑、锐化等,滤波器的设计依赖于人类的先验知识,例如高斯滤波器用于去噪,Sobel滤波器用于边缘检测。Kernel:卷积神经网络中的卷积核参数则通过反向传播算法和梯度下降优化自动学习的,能够在不同的任务中学习到特定的、复杂的特征。Filter多用于低层次的图像处理 ,如平滑、锐化、边缘检测等,它通常应用于图像的像素级操作。Kernel则可以在不同层次的特征提取中应用。例如在CNN的前层,它可能类似于传统滤波器,提取简单的边缘和纹理信息;而在更深的层次,它可以提取更抽象的特征,帮助进行高层次的任务,如物体识别、语义分割等。
可以认为,CNN中的卷积核是传统滤波器概念在深度学习中的自然扩展和进化版本。
2.1.2 卷积函数filter2D
filter2D 是 OpenCV 中用于对图像进行二维卷积操作的一个函数,它允许使用自定义的滤波器(卷积核)对图像进行各种滤波处理,其语法为:
python
dst = cv2.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])-
src::输入图像(可以是灰度图或彩色图像)。 -
ddepth:输出图像的深度,即像素数据类型,可以是以下类型之一:CV_8U:无符号8位整数。CV_16U:无符号16位整数。CV_16S:有符号16位整数。CV_32F:32位浮点数。CV_64F:64位浮点数。- 若设置为
-1,则输出图像与输入图像的深度相同。
-
kernel:卷积核(滤波器)。这是一个大小为(m, n)的二维矩阵,用于卷积操作。 -
.
dst(可选)::输出图像的存储位置。如果不提供,函数会自动创建一个与输入图像大小和类型相同的图像。 -
anchor(可选):卷积核的锚点。默认为(-1, -1),表示锚点位于卷积核的中心。你可以将其设置为其他值来改变卷积核的相对位置。 -
delta(可选):用于在卷积结果中添加一个常量偏移。默认值为0。 -
borderType(可选):边界填充方法,用于处理图像边界问题。常见的边界类型包括:cv2.BORDER_CONSTANT: 填充常数值。cv2.BORDER_REPLICATE: 重复最近的边界像素。cv2.BORDER_REFLECT: 反射边界。cv2.BORDER_WRAP: 环绕边界。cv2.BORDER_DEFAULT: 使用默认的边界策略。
以下是使用 filter2D 进行图像平滑的一个示例:
python
import cv2
import numpy as np
#导入图片
img = cv2.imread('./dog.jpeg')
kernel = np.ones((5, 5), np.float32) / 25 # 5×5的均值滤波器
dst = cv2.filter2D(img, -1, kernel) # ddepth = -1 表示图片的数据类型不变
# 很明显卷积之后的图片模糊了.
cv2.imshow('img', np.hstack((img, dst)))
cv2.waitKey(0)
cv2.destroyAllWindows()
在这个示例中,使用了一个 3x3 的均值滤波器来平滑图像。原始图片中的每个点都被平均了一下, 所以图像变模糊了.。你可以根据需求设计不同的卷积核,例如用于边缘检测、锐化等。常见卷积核:
-
均值滤波器(用于平滑图像):
pythonkernel = np.ones((3, 3), np.float32) / 9 -
锐化滤波器(用于图像锐化):
pythonkernel = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]]) -
Sobel 滤波器(用于边缘检测):
pythonkernel = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
2.1.3 滤波器分类
| 功能 | 滤波器类型 | 描述 |
|---|---|---|
| 去噪 | 均值滤波器、高斯滤波器、中值滤波器 | 用于去除图像中的随机噪声 |
| 边缘检测 | 高通滤波器(Sobel、Canny 边缘检测) | 用于检测图像中的边缘信息 |
| 图像增强 | 锐化滤波器 | 用于提高图像的细节对比度,增强图像细节 |
| 图像平滑 | 低通滤波器(高斯模糊) | 通过减少高频噪声实现图像平滑 |
| 保边去噪 | 双边滤波器 | 在去除噪声的同时保留图像的边缘细节 |
根据以上应用场景,滤波器可以分为以下几种主要类型:
| 滤波器类型 | 作用 | 原理 | 常见类型 |
|---|---|---|---|
| 低通滤波器(LPF) | 平滑图像,去除噪声和细节 | 抑制高频成分(即快速变化的像素) 保留低频成分 (即平滑部分) | 方盒滤波(Box Filter) :平均周围像素值来平滑图像 均值滤波器(Mean Filter) :计算周围像素的平均值 高斯滤波器(Gaussian Filter) :使用高斯函数对像素进行加权平均。 |
| 高通滤波器(HPF) | 增强图像的边缘或细节 | 抑制低频成分,突出高频成分 | Sobel滤波器 :用于检测边缘。 Laplacian滤波器: 用于增强图像细节 |
| 中值滤波器(Median Filter) | 去除椒盐噪声 (salt-and-pepper noise) | 替换当前像素值为邻域内像素的中值,去除孤立噪声点 | 无 |
| 双边滤波器(Bilateral Filter) | 保留边缘的情况下平滑图像 | 结合空间邻域与像素值相似度,保留边缘 | 无 |
| 自适应滤波器(Adaptive Filter) | 处理不均匀噪声 | 根据局部统计特性调整滤波器参数 | 无 |
2.2 降噪
2.2.1 方盒滤波器
方盒滤波器(boxFilter ) 的滤波器核(卷积核)是一种均匀的矩阵,每个元素的值相同。这样计算时,每个像素的值由周围的像素值的平均值决定,因此能够去除噪声,但图像的边缘可能会变得模糊。其语法为:
python
boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]])src:输入图像ddepth:输出图像的深度ksize:滤波器的大小normalize:是否对计算结果进行归一化。
例如一个3×3的方盒滤波器,未归一化时卷积核是:
python
[1, 1, 1]
[1, 1, 1]
[1, 1, 1]这种情况下,卷积的结果是该局部区域内所有像素的简单累加和,不做平均处理。这样操作的结果会可能超出正常的像素范围(0-255),但对于某些特殊应用场景,这样做可能有特定用途。
归一化时的卷积核是:
python
[1/9, 1/9, 1/9]
[1/9, 1/9, 1/9]
[1/9, 1/9, 1/9]这种情况下,最终得到的结果会是区域内像素的平均值,方盒滤波器等价于均值滤波器。
python
# 方盒滤波
import cv2
import numpy as np
img = cv2.imread('dog.jpeg')
# 不用手动创建卷积核, 只需要告诉方盒滤波, 卷积核的大小是多少.
dst = cv2.boxFilter(img, -1, (5, 5), normalize=True)
cv2.imshow('img', np.hstack((img, dst)))
cv2.waitKey(0)
cv2.destroyAllWindows()
2.2.2 均值滤波器
blur 是 boxFilter 的简化版,即归一化的方盒滤波,可快速实现均值模糊效果,其语法为:
python
blur(src, ksize[, dst[, anchor[, borderType]]])
python
# 均值滤波
img = cv2.imread('dog.jpeg')
dst = cv2.blur(img, (5, 5))
cv2.imshow('img', np.hstack((img, dst)))
cv2.waitKey(0)
cv2.destroyAllWindows()2.2.3 高斯滤波器
2.2.3.1 高斯函数
高斯分布(正态分布)是一种常见的概率分布,用来描述数据在均值附近集中、且两端逐渐减少的分布形式。它的概率密度函数正是一个一维的高斯函数,定义如下:
G ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) G(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right) G(x)=2π σ1exp(−2σ2(x−μ)2)
x是输入变量(如时间、空间坐标等)。μ是高斯函数的均值,表示钟形曲线的中心位置(通常是0)。σ是标准差,决定了钟形曲线的宽度,σ越大,曲线越平滑。exp()表示指数函数。

在图像处理中,我们常用的是二维高斯函数,用于高斯滤波,公式如下:
G ( x , y ) = 1 2 π σ 2 exp ( − ( x − μ x ) 2 + ( y − μ y ) 2 2 σ 2 ) G(x, y) = \frac{1}{2\pi\sigma^2} \exp\left( -\frac{(x - \mu_x)^2 + (y - \mu_y)^2}{2\sigma^2} \right) G(x,y)=2πσ21exp(−2σ2(x−μx)2+(y−μy)2)
(x, y)是二维空间中的坐标。μ_x和μ_y是高斯函数的中心点坐标。σ是标准差,控制滤波器的范围和影响。
2.2.3.2 高斯滤波器
使用符合高斯分布的卷积核对图像进行卷积,以平滑图像。高斯模糊通过邻域像素的加权平均来减少噪声,其中靠近中心的像素权重大,远离中心的像素权重小。其本质是对图像中的每一个像素点,通过其周围像素的加权平均值来进行模糊处理,通常适用于减少图像中的随机噪声,其特点是:
- 可以有效降低图像中的高频噪声或减少图像中的随机点
- 对所有像素均一处理,因此边缘也会被模糊
- 计算速度快,常用于一般的噪声去除和图像预处理
高斯滤波的重点就是如何计算符合高斯分布的卷积核(高斯模板)。假设卷积核尺寸为3×3,中心点的坐标是(0,0),则9个格子的坐标如下图左侧所示。我们假设 σ = 1.5 \sigma=1.5 σ=1.5,代入二维高斯函数公式,可计算出整个卷积核为:

- 计算
(0,0)坐标点,对应的值: 1 / ( 2 ∗ n p . p i ∗ 1.5 ∗ ∗ 2 ) = 0.00707355 1 / (2 * np.pi * 1.5**2)=0.00707355 1/(2∗np.pi∗1.5∗∗2)=0.00707355- 计算
(-1, 1)坐标点对应的值 1 / ( 2 ∗ n p . p i ∗ 1.5 ∗ ∗ 2 ) ∗ n p . e x p ( − ( 2 / ( 2 ∗ 1.5 ∗ ∗ 2 ) ) ) = 0.0453542 1 / (2 * np.pi * 1.5**2)* np.exp(-(2/(2*1.5**2)))=0.0453542 1/(2∗np.pi∗1.5∗∗2)∗np.exp(−(2/(2∗1.5∗∗2)))=0.0453542
我们可以观察到越靠近中心,数值越大;越边缘的数值越小,符合高斯分布的特点。
通过高斯函数计算出来的是概率密度函数,而这9个点的权重总和等于0.4787147。为了确保这九个点加起来和为1,上面9个值还要分别除以0.4787147,得到最终的高斯模板。有些高斯模板都是整数值,这是对模板中每个数除上左上角的值,,然后取整得到的结果。

卷积核确定了之后,就可以进行卷积计算了。将下面这9个值加起来,就是中心点的高斯滤波的值。对所有点重复这个过程,就得到了高斯模糊后的图像。

在OpenCV中,我们使用GaussianBlur进行高斯滤波计算,通过应用高斯滤波器(Gaussian filter)来平滑图像,减少噪声和细节,使图像看起来更平滑。其语法为:
python
GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])src:输入图像,可以是彩色图像(BGR)或灰度图像。ksize:高斯核的大小,必须是正的奇数,例如(5,5)。sigmaX:X方向上的标准差(控制模糊程度)。当sigmaX值为 0 时,OpenCV 会根据ksize自动计算。sigmaY(可选):Y方向上的标准差。如果这个值为 0,函数将使用sigmaX的值。borderType(可选):边界模式,决定如何处理图像边界。默认值为cv2.BORDER_DEFAULT。
python
import cv2
# 读取图像
image = cv2.imread('lena.jpg')
# 使用 GaussianBlur
blurred_image = cv2.GaussianBlur(image, (5, 5), 1)
# 显示图像
cv2.imshow('Blurred Image', blurred_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
sigma越大, 平滑(模糊)效果越明显

没有指定sigma时, ksize越大,平滑效果越明显
如果对经典的gaussian.png进行处理,效果如下,原图中很细小的白点被消除了:

2.2.4 中值滤波器
中值滤波器(medianBlur)的原理就是对每个卷积窗口中的所有像素值进行排序,然后取中间值作为卷积计算结果。这种操作在去除椒盐噪声等突变噪声(salt-and-pepper noise)方面特别有效。
在含有椒盐噪声的图像中,像素值要么非常高(白点),要么非常低(黑点)。中值滤波器能够很好地将这些异常点替换为邻域中更接近的值,从而有效去除这种噪声。
假设我们有一个 3x3 的图像区域(卷积窗口),如下所示:
python
src=array([[74, 67, 71],
[74, 69, 71],
[66, 68, 73]], dtype=uint8)如果我们用一个 3x3 的中值滤波器来处理这个窗口,先将这个区域的所有元素按数值大小进行排序:
python
[66, 67, 68, 69, 71, 71, 73, 74, 74]选择排序后的中间值,即第 5 个元素值71就是此区域中心点的卷积计算结果。
在opencv中,我们使用cv2.medianBlur进行中值滤波计算,其语法为:
python
dst = cv2.medianBlur(src, ksize)src: 输入图像ksize: 滤波器的大小,必须是正奇数(如 3, 5, 7 等)。窗口的尺寸越大,滤波效果越明显,但图像可能会变得更模糊。
下面是中值滤波的处理效果(ksize=5):

2.2.5 双边滤波器

这是OpenCV中的一张经典图片,可以看到照片中的女人,帽子是浅黄,帽子上的装饰是蓝色,头发是棕色,脸的颜色也不一样。这样不同的部分都有一个轮廓线,相交的地方颜色变化就非常大。如果在灰度图上看,差异更大,边界左右的像素很可能一个是白色一个是黑色(灰度距离)。高斯滤波器只考虑像素之间的空间信息,所以处理后容易模糊掉物体的边界。
2.2.5.1 工作原理
双边滤波是结合空域和色域的滤波器。同时考虑像素的空间距离和像素强度差异。在滤波过程中,离中心像素越近的像素会权重越大,而颜色和中心像素差异越大的像素权重越小,这样边界处颜色不容易被混合,所以双边滤波可以在保持边缘清晰的情况下,去除图像中的噪声,适合高质量图像处理。
可以简单理解为不对边界进行模糊。
- 空间距离 :当前点于中心点的欧氏距离,空间域高斯函数形式如下,用于根据像素的物理距离来加权计算,保证距离中心像素越远的像素权重越小。
G σ s ( x i , x ) = exp ( − ∥ x i − x ∥ 2 2 σ s 2 ) G_{\sigma_s}(x_i, x) = \exp\left(-\frac{\|x_i - x\|^2}{2\sigma_s^2}\right) Gσs(xi,x)=exp(−2σs2∥xi−x∥2)
- G σ s ( x i , x ) G_{\sigma_s}(x_i, x) Gσs(xi,x):表示邻域中像素位置 x i x_i xi 相对于中心像素 x x x 的空间距离权重;
- ∥ x i − x ∥ \|x_i - x\| ∥xi−x∥:表示像素 x i x_i xi 和中心像素 x x x 之间的欧几里得距离(通常为二维距离,考虑的是像素位置的坐标差异);
- σ s \sigma_s σs:控制空间权重的标准差,值越大,意味着更大范围内的像素影响越大。
- 灰度距离 :当前点灰度于中心点灰度差的绝对值,其高斯函数形式如下。该函数用于根据像素的灰度值差异来加权计算,确保与中心点灰度差异越大的像素权重越小,从而保留边缘。
G σ r ( I ( x i ) , I ( x ) ) = exp ( − ( I ( x i ) − I ( x ) ) 2 2 σ r 2 ) G_{\sigma_r}(I(x_i), I(x)) = \exp\left(-\frac{(I(x_i) - I(x))^2}{2\sigma_r^2}\right) Gσr(I(xi),I(x))=exp(−2σr2(I(xi)−I(x))2)
- G σ r ( I ( x i ) , I ( x ) ) G_{\sigma_r}(I(x_i), I(x)) Gσr(I(xi),I(x)):表示邻域中像素 x i x_i xi 的灰度值 I ( x i ) I(x_i) I(xi) 相对于中心像素 I ( x ) I(x) I(x) 的灰度差异权重;
- I ( x i ) − I ( x ) I(x_i) - I(x) I(xi)−I(x):表示像素 x i x_i xi 和中心像素 x x x 之间的灰度值差异;
- σ r \sigma_r σr:控制灰度值权重的标准差,值越大,意味着更大灰度差异的像素也可以有较高的权重。
使用灰度距离而不是RGB色空间的距离,能够简化计算、提高效率,并且更符合人类视觉对图像的感知需求。由于亮度是影响图像结构和轮廓的主要因素,灰度值已足够用于保持边缘细节,同时减少噪声。
双边滤波时,最终的权重 W ( x i , x ) W(x_i, x) W(xi,x) 是这两个高斯函数的乘积:
W ( x i , x ) = G σ s ( x i , x ) ⋅ G σ r ( I ( x i ) , I ( x ) ) W(x_i, x) = G_{\sigma_s}(x_i, x) \cdot G_{\sigma_r}(I(x_i), I(x)) W(xi,x)=Gσs(xi,x)⋅Gσr(I(xi),I(x))
处理后的像素值为:
I ′ ( x ) = 1 W p ∑ x i ∈ Ω I ( x i ) W ( x i , x ) I'(x) = \frac{1}{W_p} \sum_{x_i \in \Omega} I(x_i) W(x_i, x) I′(x)=Wp1xi∈Ω∑I(xi)W(xi,x)
- I ′ ( x ) I'(x) I′(x) :滤波后的位置 x x x 处的像素值;
- I ( x i ) I(x_i) I(xi) :邻域 Ω \Omega Ω 中位置 x i x_i xi 处的像素值;
- W p W_p Wp :权重的归一化系数,确保滤波后的像素值不超出范围。
该权重结合了空间距离和灰度差异,使得双边滤波可以同时对图像进行平滑和边缘保留处理。
- σ s \sigma_s σs:控制空间距离的影响范围,值越大,滤波的模糊效果越强。
- σ r \sigma_r σr:控制灰度差异的敏感性,值越大,保留边缘的能力减弱,值越小,边缘保留能力增强。
- 由于总的权重是两个权重的乘积,所以其速度与比一般的滤波慢很多(计算复杂度为核大小的平方)
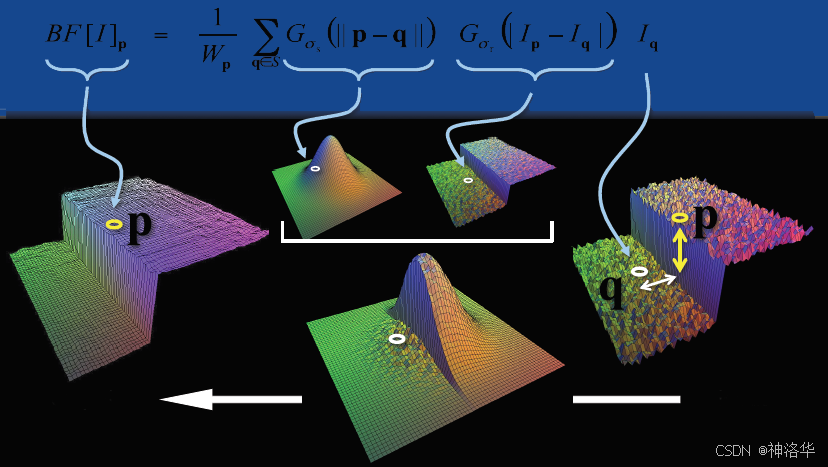
上图可以理解为和
p灰度近似的区域使用高斯滤波,和p灰度显著差异的q区域,权重会很小,几乎被忽略。
2.2.5.2 bilateralFilter
OpenCV中使用bilateralFilter进行双边滤波处理,其语法为:
python
bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])src:输入图像。d:卷积核大小sigmaColor:在颜色空间中的滤波器 σ \sigma σ 值。sigmaSpace:在坐标空间中的滤波器 σ \sigma σ 值。
python
import cv2
import numpy as np
img = cv2.imread('./lena.png')
dst = cv2.bilateralFilter(img, 7, 20, 50)
cv2.imshow('img', np.hstack((img, dst)))
cv2.waitKey(0)
cv2.destroyAllWindows()
右图是处理之后的结果,可以看到脸部变得更加平滑,有美颜的效果。而如果用双边滤波处理椒盐噪声,就没有效果。因为这些噪声点和周围像素的灰度值差异很大,而差异大的部分双边滤波是不处理的。
2.3 边缘检测
2.3.1 sobel算子
边缘是像素值发生跃迁的位置,是图像的显著特征之一,在图像特征提取,对象检测,模式识别等方面都有重要的作用。例如,当图像中一侧较亮,另一侧较暗时,人眼会很容易将这一过渡区域识别为边缘,也就是像素的灰度值快速变化的地方(梯度大的地方)。
由于图像是以像素为单位的离散数据,无法直接应用连续的微分运算,所以需要采用差分运算来计算图像中像素灰度的变化。差分算子通过以下几种基本方式近似图像中某一方向的梯度(导数):
- 一阶前向差分:当前像素与下一个像素的差值。
f ′ ( x ) ≈ f ( x + 1 ) − f ( x ) ] f'(x) \approx f(x+1) - f(x) ] f′(x)≈f(x+1)−f(x)]
- 一阶后向差分:当前像素与前一个像素的差值。
f ′ ( x ) ≈ f ( x ) − f ( x − 1 ) ] f'(x) \approx f(x) - f(x-1) ] f′(x)≈f(x)−f(x−1)]
- 中心差分:用当前像素的前后两个像素的差值来计算当前像素点的导数。 这种方式对称性更好、误差更小。
f ′ ( x ) ≈ f ( x + 1 ) − f ( x − 1 ) 2 ] f'(x) \approx \frac{f(x+1) - f(x-1)}{2} ] f′(x)≈2f(x+1)−f(x−1)]
Sobel 算子是一种基于离散差分的边缘检测算子,它通过计算图像亮度值在水平和垂直方向的近似梯度,来检测图像中的边缘。其核心思想是应用两个3x3的卷积核,分别计算图像在水平方向(x方向)和垂直方向(y方向)的梯度。梯度越大,说明像素在该方向的变化越大,边缘信号越强。
-
水平方向卷积核 G x G_x Gx:
x轴差分模式,检测图像在水平方向的亮度变化。G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} Gx= −1−2−1000121
-
垂直方向卷积核 G y G_y Gy:
y轴差分模式,检测图像在垂直方向的亮度变化。G y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} Gy= −101−202−101
计算之后,我们可以得到水平方向梯度 G x G_x Gx和垂直方向梯度: G y G_y Gy。结合这两个方向的梯度,得到该像素点的梯度大小,反映了边缘的强度: G = G x 2 + G y 2 G = \sqrt{G_x^2 + G_y^2} G=Gx2+Gy2 或者采用绝对值相加近似计算: G = ∣ G x ∣ + ∣ G y ∣ G = |G_x| + |G_y| G=∣Gx∣+∣Gy∣
梯度的方向(该点边缘的方向)可以通过计算 G x G_x Gx 和 G y G_y Gy 的比值得到:
θ = arctan ( G y G x ) \theta = \arctan\left(\frac{G_y}{G_x}\right) θ=arctan(GxGy)
在实际应用中,Sobel算子广泛用于边缘检测、图像锐化等任务。你可以通过 OpenCV 提供的cv2.Sobel函数来进行计算。
python
Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) -> dstsrc:输入图像,通常是一个灰度图像。ddepth:输出图像的深度(数据类型),常用值为cv2.CV_64F,也可以使用cv2.CV_8U,cv2.CV_16U,或者直接写-1(表示和原图一致)。dx: x 方向上的导数阶数。dx=1表示在 x 方向上计算一阶导数,dx=0则不在 x 方向上计算。dy: y 方向上的导数阶数。dy=1表示在 y 方向上计算一阶导数,dy=0则不在 y 方向上计算。ksize: 卷积核大小,必须为奇数(1, 3, 5, 7等)。ksize越大,结果越平滑,但同时细节也可能丢失。ksize=-1时,Sobel 算子就是 Scharr 算子。scale: 可选参数,缩放导数的比例系数,默认为 1。delta: 可选参数,表示添加到结果的值,默认为 0。borderType: 用于指定如何处理边界像素,默认为cv2.BORDER_DEFAULT。
下面是一个简单的示例:
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
img = cv2.imread('./chess.png')#
dx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5) # 水平方向梯度,只有垂直方向的边缘
dy = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5) # 垂直方向梯度,只有水平方向的边缘
# 如果使用dst = cv2.magnitude(dx, dy),dst亮度会更高。
dst = cv2.add(dx, dy) # 使用addWeighted也可以
plt.figure(figsize=[20,5])
plt.subplot(141);plt.imshow(img,cmap='gray');plt.title("img");
plt.subplot(142);plt.imshow(dx,cmap='gray');plt.title("dx");
plt.subplot(143);plt.imshow(dy,cmap='gray');plt.title("dy");
plt.subplot(144);plt.imshow(dst,cmap='gray');plt.title("dst");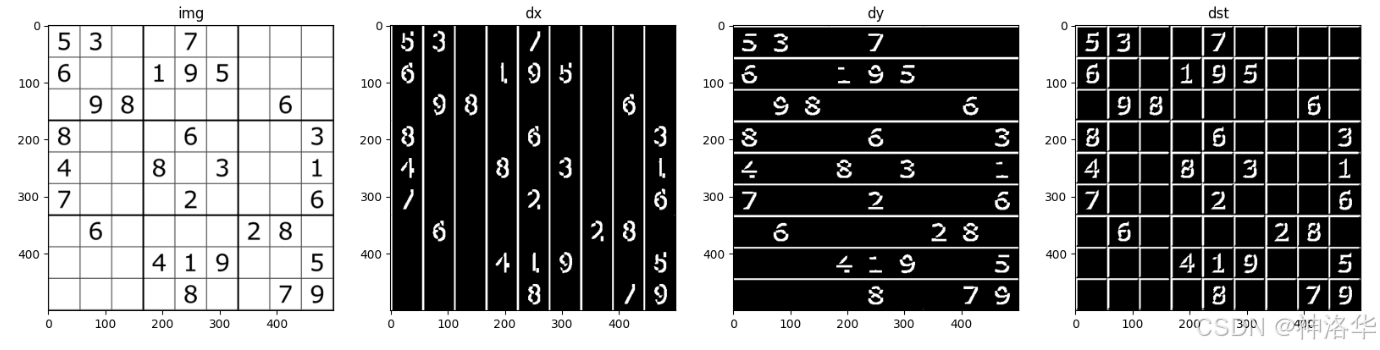
如果设ddepth=-1而非cv2.CV_64F,效果如下:

2.3.2 Scharr算子
Sobel 算子使用的卷积核较为简单,但它并不是精确的导数计算,仅仅是一个近似。对于边缘检测任务,导数的近似可能不足以捕捉图像中的高频变化,尤其是在边缘强度变化剧烈的地方。当内核较小时(比如ksize=3),这种近似可能会放大误差,使得图像中的细节丢失或边缘模糊。
为了解决这一问题,OpenCV 提供了沙尔( Scharr )算子,它对内核大小为 3 时进行了优化,特别在检测图像中的细小边缘时,计算结果更精确,并且运算速度与 Sobel 算子相当。
Scharr 算子计算过程与Sobel算子类似,但卷积核系数更大,放大了像素变换的情况,增强了对图像细节的捕捉能力。
- 水平方向: G x = [ 3 0 − 3 10 0 − 10 3 0 − 3 ] G_x = \begin{bmatrix} 3 & 0 & -3 \\ 10 & 0 & -10 \\ 3 & 0 & -3 \end{bmatrix} Gx= 3103000−3−10−3
- 垂直方向: G y = [ 3 10 3 0 0 0 − 3 − 10 − 3 ] G_y = \begin{bmatrix} 3 & 10 & 3 \\ 0 & 0 & 0 \\ -3 & -10 & -3 \end{bmatrix} Gy= 30−3100−1030−3
你可以使用cv2.Scharr函数进行计算:
python
Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]) -> dst
python
img = cv2.imread('./lena.png')
dx = cv2.Scharr(img, cv2.CV_64F, dx=1, dy=0)
dy = cv2.Scharr(img, cv2.CV_64F, dx=0, dy=1)
dst = cv2.addWeighted(dx, 0.5, dy, 0.5, gamma=0)
plt.figure(figsize=[20,5])
plt.subplot(141);plt.imshow(img[:,:,::-1]);plt.title("img");
plt.subplot(142);plt.imshow(dx,cmap='gray');plt.title("dx");
plt.subplot(143);plt.imshow(dy,cmap='gray');plt.title("dy");
plt.subplot(144);plt.imshow(dst,cmap='gray');plt.title("dst");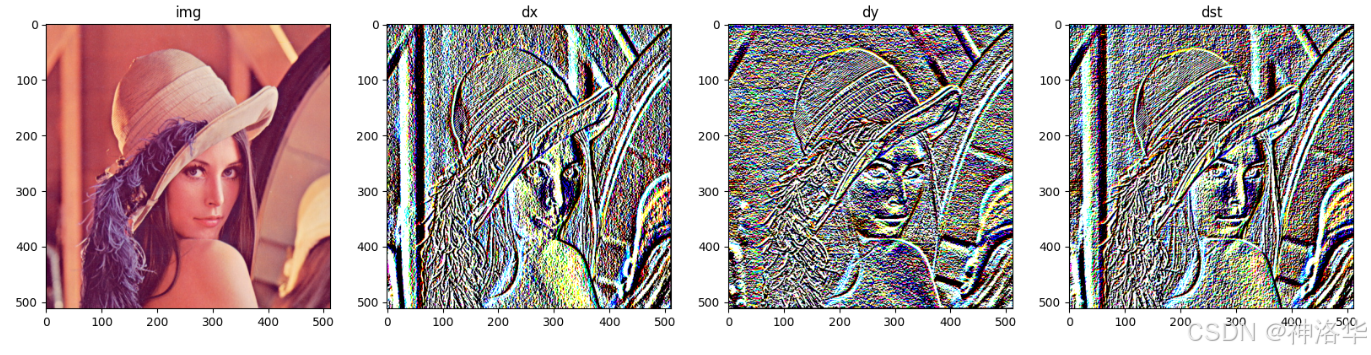
2.3.3 Laplacian算子
Sobel 算子是通过模拟一阶导数来进行边缘检测,一阶导数变化越大的地方,边缘强度越强。那如果继续对一阶导数f'(t)求导呢?如下图右侧所示,可以发现边缘处的二阶导数f''(t)=0, 我们可以利用这一特性去寻找图像的边缘。

Laplacian算子就是利用了这一思路,通过计算图像的二阶导数,来进行边缘检测。需要注意的是,二阶求导为0的位置也可能是无意义的位置,这些位置一般都是噪声,所以在使用Laplacian算子之前,通常需要对图像进行预平滑处理(如高斯模糊)。Laplacian滤波器推导过程如下:
-
x轴方向:- 一阶差分: f ′ ( x ) = f ( x ) − f ( x − 1 ) f'(x) = f(x) - f(x - 1) f′(x)=f(x)−f(x−1)
- 二阶差分: f ′ ′ ( x ) = f ′ ( x + 1 ) − f ′ ( x ) = ( f ( x + 1 ) − f ( x ) ) − ( f ( x ) − f ( x − 1 ) ) f''(x) = f'(x+1) - f'(x) = (f(x + 1) - f(x)) - (f(x) - f(x - 1)) f′′(x)=f′(x+1)−f′(x)=(f(x+1)−f(x))−(f(x)−f(x−1))
- 化简后: f ′ ′ ( x ) = f ( x − 1 ) − 2 f ( x ) ) + f ( x + 1 ) f''(x) = f(x - 1) - 2 f(x)) + f(x + 1) f′′(x)=f(x−1)−2f(x))+f(x+1)
-
y轴方向:同理可得 f ′ ′ ( y ) = f ( y − 1 ) − 2 f ( y ) ) + f ( y + 1 ) f''(y) = f(y - 1) - 2 f(y)) + f(y + 1) f′′(y)=f(y−1)−2f(y))+f(y+1) -
x轴,y轴梯度叠加:f ′ ′ ( x , y ) = f x ′ ( x , y ) + f y ′ ( x , y ) f''(x,y) = f'_x(x,y) + f'_y(x,y) f′′(x,y)=fx′(x,y)+fy′(x,y)
f ′ ′ ( x , y ) = f ( x − 1 , y ) − 2 f ( x , y ) ) + f ( x + 1 , y ) + f ( x , y − 1 ) − 2 f ( x , y ) ) + f ( x , y + 1 ) f''(x,y) = f(x - 1, y) - 2 f(x,y)) + f(x + 1, y) + f(x, y - 1) - 2 f(x,y)) + f(x,y + 1) f′′(x,y)=f(x−1,y)−2f(x,y))+f(x+1,y)+f(x,y−1)−2f(x,y))+f(x,y+1)
f ′ ′ ( x , y ) = f ( x − 1 , y ) + f ( x + 1 , y ) + f ( x , y − 1 ) + f ( x , y + 1 ) − 4 f ( x , y ) ) f''(x,y) = f(x - 1, y) + f(x + 1, y) + f(x, y - 1) + f(x,y + 1) - 4 f(x,y)) f′′(x,y)=f(x−1,y)+f(x+1,y)+f(x,y−1)+f(x,y+1)−4f(x,y))
这个等式可以用矩阵写成:
f ′ ′ ( x , y ) = [ 0 1 0 1 − 4 1 0 1 0 ] ⨀ [ f ( x − 1 , y − 1 ) f ( x , y − 1 ) f ( x + 1 , y − 1 ) f ( x − 1 , y ) f ( x , y ) f ( x + 1 , y ) f ( x − 1 , y + 1 ) f ( x , y + 1 ) f ( x + 1 , y + 1 ) ] f''(x,y) = \left[\begin{matrix}0 & 1 & 0\\1 & -4 & 1\\0 & 1 & 0\end{matrix}\right] \bigodot \left[\begin{matrix}f(x-1, y-1) & f(x, y-1) & f(x+1,y-1)\\f(x-1,y) & f(x,y) & f(x+1,y)\\f(x-1,y+1) & f(x,y+1) & f(x+1,y+1)\end{matrix}\right] f′′(x,y)= 0101−41010 ⨀ f(x−1,y−1)f(x−1,y)f(x−1,y+1)f(x,y−1)f(x,y)f(x,y+1)f(x+1,y−1)f(x+1,y)f(x+1,y+1)
这样就得到了拉普拉斯算子3x3的卷积核:
0 1 0 1 − 4 1 0 1 0 \] \\begin{bmatrix} 0 \& 1 \& 0 \\\\ 1 \& -4 \& 1 \\\\ 0 \& 1 \& 0 \\end{bmatrix} 0101−41010 `cv2.Laplacian()`函数语法为: ```python # 直接对图像求二阶导数,不区分水平垂直方向 Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]]) -> dst ``` 简单示例: ```python import cv2 import numpy as np img = cv2.imread('./chess.png') Gaussian= cv2.GaussianBlur(img, (5, 5), 5) dst = cv2.Laplacian(Gaussian, -1, ksize=5) plt.figure(figsize=[20,6]) plt.subplot(131);plt.imshow(img[:,:,::-1]);plt.title("img"); plt.subplot(132);plt.imshow(Gaussian[:,:,::-1]);plt.title("Gaussian"); plt.subplot(133);plt.imshow(dst,cmap='gray');plt.title("Laplacian"); ``` 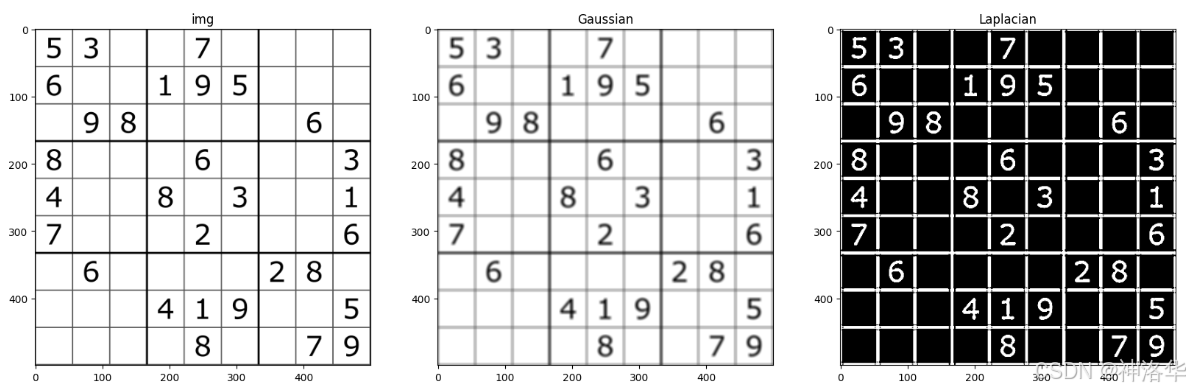 可见处理棋盘的效果比`Sobel` 算子更好,但是处理人物图效果一般。 ```python img = cv2.imread('./lena.png') Gaussian= cv2.GaussianBlur(img, (5, 5), 5) Gaussian=cv2.cvtColor(Gaussian, cv2.COLOR_BGR2GRAY) dst = cv2.Laplacian(Gaussian, -1, ksize=5) plt.figure(figsize=[20,6]) plt.subplot(131);plt.imshow(img[:,:,::-1]);plt.title("img"); plt.subplot(132);plt.imshow(Gaussian,cmap='gray');plt.title("Gaussian"); plt.subplot(133);plt.imshow(dst,cmap='gray');plt.title("Laplacian"); ```  ##### 2.3.4 Canny OpenCV 中的 `Canny`是一种经典的边缘检测方法,旨在找到图像中强烈变化的像素位置,从而检测到图像的边缘。Canny 算法具有多个步骤,能够实现可靠且精确的边缘检测。其主要原理为: 1. 高斯滤波(Gaussian Filter): 由于图像中的噪声可能会影响边缘检测结果,Canny 算法的第一步是使用高斯滤波器对图像进行平滑处理。高斯滤波能够去除图像中的噪声,同时保留边缘信息。这一步骤有助于减少误检。 2. **计算梯度(Gradient Calculation)** : 通过对图像进行 **Sobel 算子** 或 **Roberts 算子** 计算梯度,生成水平和垂直两个方向的梯度图 G x , G y G_x,G_y Gx,Gy,然后得到图像中每个像素的梯度幅值和梯度方向: * **梯度幅值** : G = G x 2 + G y 2 G = \\sqrt{G_x\^2 + G_y\^2} G=Gx2+Gy2 * **梯度方向** : θ = arctan G y G x \\theta = \\arctan{\\frac{G_y}{G_x}} θ=arctanGxGy。梯度的方向被归为四类:------垂直,、水平、左下、右上。 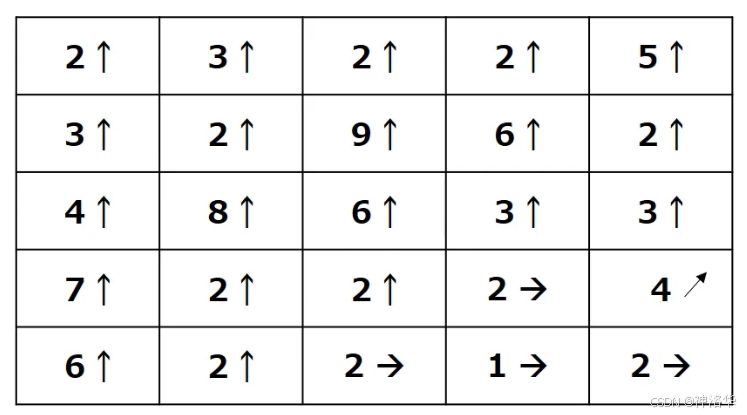 同时包含梯度值和梯度方向 3. **非极大值抑制(Non-Maximum Suppression)**: * 目的:在获取了梯度和方向后,遍历图像,去除所有不是边界的点。目的是为了细化边缘。 * 实现方法:逐个遍历像素点, 判断当前像素点是否是周围像素点中具有相同方向梯度的最大值。如果是,则被保留为潜在的边缘点。 比如下图中,点A、B、C都靠近边缘,且具有相同的梯度方向。其中A的梯度值最大,则保留该点,其它点被抑制(归零)。这样只保留真正的边缘点A,防止边缘变得过宽,增强边缘清晰度。 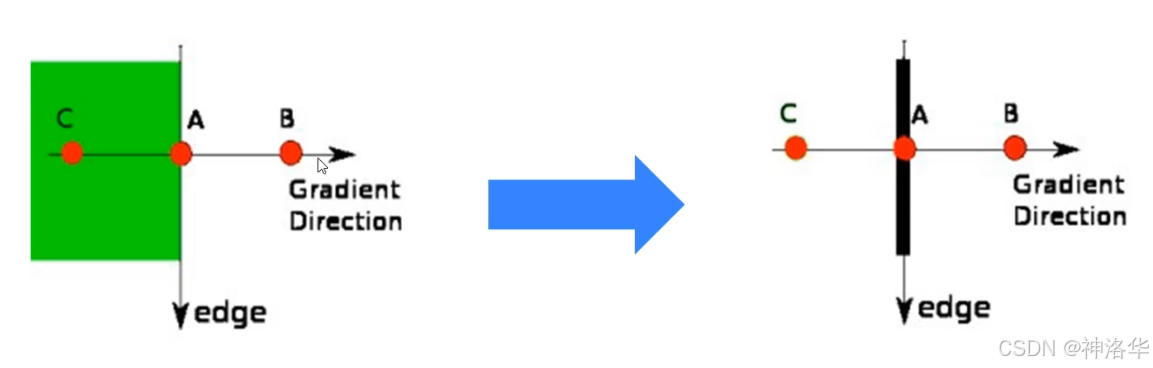 经过NMS处理后的结果是(保留每一列同方向的最大值): 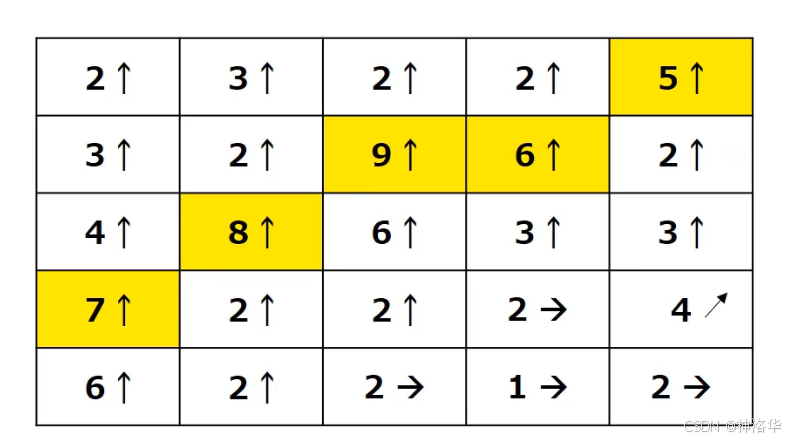 4. **双阈值检测(Double Thresholding)** : 上一步处理的结果可能有错漏,所以增加一个判定。根据用户提供的两个阈值来判定强边缘和弱边缘。 * **强边缘**:大于高阈值的像素被认为是强边缘,一定会被保留。小于低阈值的像素将直接被忽略。 * **弱边缘** :在高低阈值之间的像素被认为是弱边缘,如果此弱边缘与强边缘相连,则将其视为真正的边缘;否则将其丢弃。这一步骤能够去除噪声中的虚假边缘并保持真正的边缘。 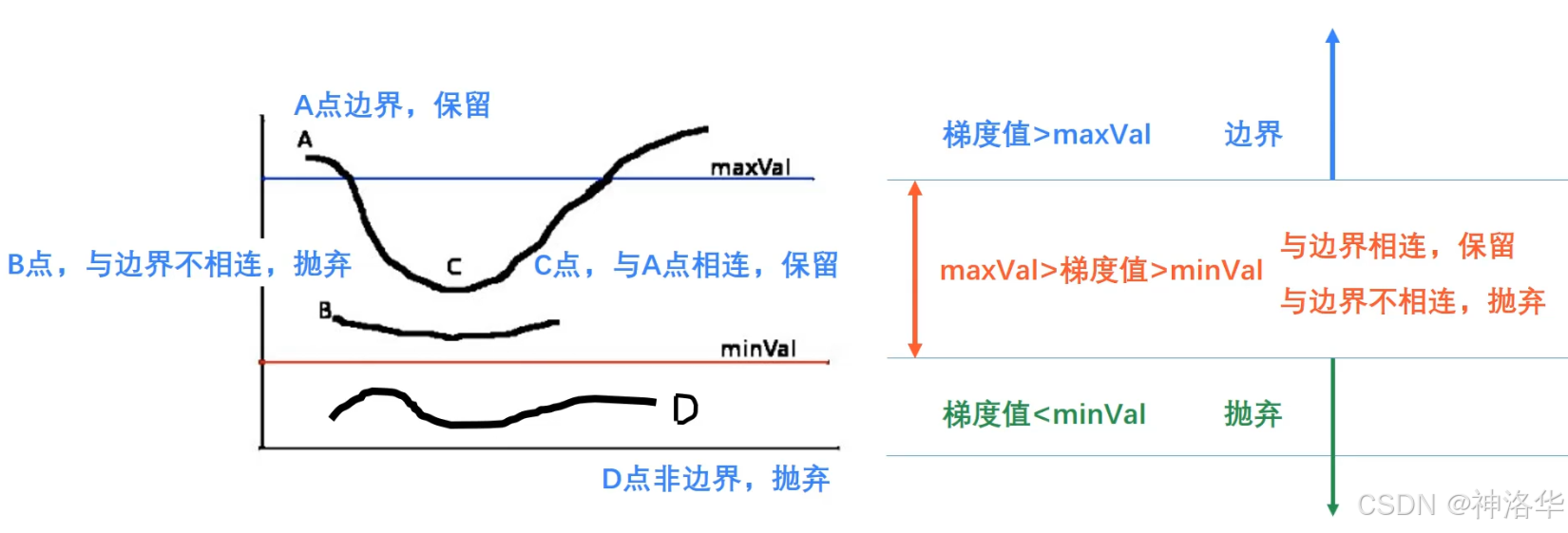 5. **最终输出** : 经过以上步骤后,Canny 算法会输出一个二值化图像,其中边缘部分的为白色,其它区域为黑色。 我们可以通过`cv2.Canny`函数进行计算: ```python Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]]) -> edges ``` * **image**:输入图像,必须是单通道灰度图像。 * **threshold1**:低阈值。 * **threshold2**:高阈值。 * **apertureSize** (可选):Sobel 算子的大小,默认为 3。 * **L2gradient** (可选): 布尔类型。如果为 `True`,将使用更精确的 L2 范数来计算梯度幅值,即 `sqrt((dI/dx)^2 + (dI/dy)^2)`。如果为 `False`,则使用 L1 范数,即 `|dI/dx| + |dI/dy|`,默认为 `False`。 ```python import cv2 import numpy as np import matplotlib.pyplot as plt %matplotlib inline img = cv2.imread('./lena.png') lena1 = cv2.Canny(img,60,120) lena2 = cv2.Canny(img,80,150) lena3 = cv2.Canny(img,100,200) plt.figure(figsize=[20,6]) plt.subplot(131);plt.imshow(lena1,cmap='gray');plt.title("lena1"); plt.subplot(132);plt.imshow(lena2,cmap='gray');plt.title("lena2"); plt.subplot(133);plt.imshow(lena3,cmap='gray');plt.title("lena3"); ```  * lena1:threshold1太小,导致很多不是边缘的点没有被过滤,整张图看起来有很多杂质; * lena3:threshold2太大,一些边缘点被过滤,导致一些轮廓线断断续续,而且细节也不够丰富。 ##### 2.3.5 总结 * **Sobel算子**:广泛用于边缘检测、图像锐化等任务 * **Scharr算子**:Sobel算子的增强版,用于更精确的边缘检测,尤其适合处理细节丰富的图像。 * **Laplacian算子**:计算图像的二阶导数,用于检测图像中所有方向的快速变化区域,对噪声敏感,非常适合用来检测图像中的锐利边缘。 * **Canny边缘检测**:多步骤边缘检测算法,具有良好的精度和鲁棒性,通过双阈值和非极大值抑制减少噪声,保留显著的边缘。