MATLAB - 浮动基座机器人的逆运动学

系列文章目录

前言

本例演示如何解决以浮动底座为模型的机器人的逆运动学问题。浮动底座机器人可以在空间中自由平移和旋转，具有六个自由度。浮动基座机器人的逆运动学问题适用于空间应用，即使用安装在浮动和致动基座上的机械臂在空间操纵物体，也适用于躯干和腿部可在空间自由移动的行走机器人。

请注意，刚体树对象表示具有固定基体的刚体树。这意味着刚体树的基体在世界中具有固定的位置和方向。您可以在基体上附加一个 "浮动 "类型的刚体关节，为具有浮动基体的机器人建模，以用于动态模拟等某些应用。但是，基于梯度下降的逆运动学求解器（如 inverseKinematics 函数）不支持包含 "浮动 "类型刚体关节的刚体树对象。这是因为 IK 求解器依赖于运动学方程 Jq=˙q，该方程使用几何雅各布因子将关节位置与机器人的瞬时关节速度联系起来。由于雅各布矩阵的列数是速度自由度，因此位置自由度和速度自由度的数量必须相等才能使该方程保持有效。在这里使用浮动关节会带来差异，因为浮动关节使用四元数来表示旋转，它有四个元素，而相应的角速度只有三个元素。本示例演示了如何为浮动基座建模，以便与逆运动学函数配合使用。

有关使用浮动关节为浮动底座机器人建模的更多信息，请参阅使用浮动关节为浮动底座机器人建模。

一、浮动基座机器人建模

要对浮动基座机器人使用逆运动学求解器，必须建立一个浮动基座刚体模型，并使用六个连续的一自由度 (DOF) 关节将其连接到机器人机械手刚体树的固定基座上。这六个关节由三个棱柱关节和三个旋回关节组成，可实现沿 x、y 和 z 轴的平移和旋转。在原点构型中，它们彼此重合。

加载 ABB IRB 120 的刚体模型，将其用作浮动基座系统的机器人操纵器。

Matlab 复制代码

abbirb = loadrobot("abbIrb120",DataFormat="row");

辅助函数 floatingBaseHelper 创建了一个刚体树，其中包含六个没有惯性或质量的刚体。该函数将每个刚体串联起来，每个刚体都可以围绕世界中的某个轴自由平移或旋转。floatingBaseHelper 将浮动基底创建为一个刚体树，该刚体树可在世界中自由旋转和平移，并具有六个自由度。

Matlab 复制代码

function robot = floatingBaseHelper(df)
    arguments
        df = "column"
    end
robot = rigidBodyTree(DataFormat=df);
robot.BaseName = 'world';
jointaxname = {'PX','PY','PZ','RX','RY','RZ'};
jointaxval = [eye(3); eye(3)];
parentname = robot.BaseName;
for i = 1:numel(jointaxname)
    bname = ['floating_base_',jointaxname{i}];
    jname = ['floating_base_',jointaxname{i}];
    rb = rigidBody(bname);
    rb.Mass = 0;
    rb.Inertia = zeros(1,6);
    rbjnt = rigidBodyJoint(jname,jointaxname{i}(1));
    rbjnt.JointAxis = jointaxval(i,:);
    rbjnt.PositionLimits = [-inf inf];
    rb.Joint = rbjnt;
    robot.addBody(rb,parentname);
    parentname = rb.Name;
end
end

1.1 将机械臂安装到浮动底座上

将机械臂 abbirb 的刚体树添加到浮动底座上。组合成浮动ABBIrb 后，系统共有 12 个自由度 -- 其中 6 个是浮动底座的自由度，6 个是原机械臂的自由度（每个反卷关节一个自由度）。

Matlab 复制代码

floatingABBIrb = floatingBaseHelper("row");
addSubtree(floatingABBIrb,"floating_base_RZ",abbirb,ReplaceBase=false);

为了证明刚体树既能在空间自由平移，又能自由旋转，请将机械臂的底座置于 xyz 坐标[1.0 0.5 0.75]处，方向为[pi/4 pi/3 pi]，机械臂的关节角度为零。

Matlab 复制代码

baseOrientation = [pi/4 pi/3 pi]; % ZYX Euler rotation order
basePosition = [1.0 0.5 0.75];
robotZeroConfig = zeros(1,6);
q = [basePosition baseOrientation zeros(1,6)];
show(floatingABBIrb,q);
axis equal;
title("Robot Base ''Floating'' at Desired Position and Orientation")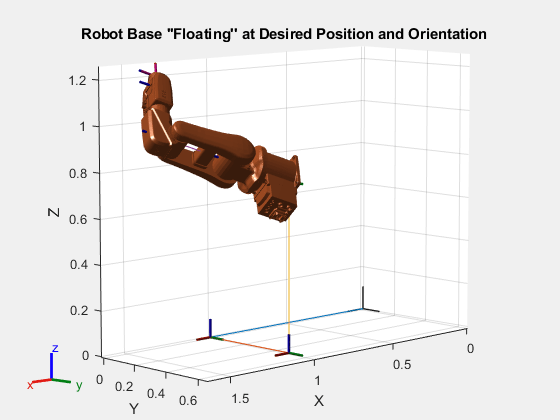

二、求解达到目标末端执行器姿势的关节构型

为了找到给定末端执行器姿势的关节值，请使用 inverseKinematics 函数。指定末端执行器主体和浮动机械臂所需的末端执行器姿势。

Matlab 复制代码

eename = "tool0";
eepose = se3([0 pi/2 1.25],"eul",[-0.25 0.45 0.25]);

创建逆运动学求解器对象，为浮动刚体树上的 eename 末端执行器找到与所需 eepose 相对应的关节值。权重为 ones(1,6)，指定求解器应考虑末端执行器的期望位置和方向。关节构型的初始假设是浮动机械臂的原点构型。

Matlab 复制代码

ik = inverseKinematics(RigidBodyTree=floatingABBIrb);
[qsoln,solninfo] = ik(eename,eepose.tform,ones(1,6),homeConfiguration(floatingABBIrb));

请注意，姿势误差规范非常小，这意味着解法足够精确。

Matlab 复制代码

disp(solninfo.Status)

三、验证关节构型

绘制所需的 eepose 和已解决的关节构型，以直观地验证末端执行器的坐标系是否与姿势一致。请注意该关节构型中的末端执行器坐标系与所需的 eepose 坐标系是一致的。

Matlab 复制代码

figure
plotTransforms(eepose,FrameSize=0.25,FrameLabel="eepose");
hold on
show(floatingABBIrb,qsoln);
hold off
axis equal
title("End Effector Reaches Desired Pose")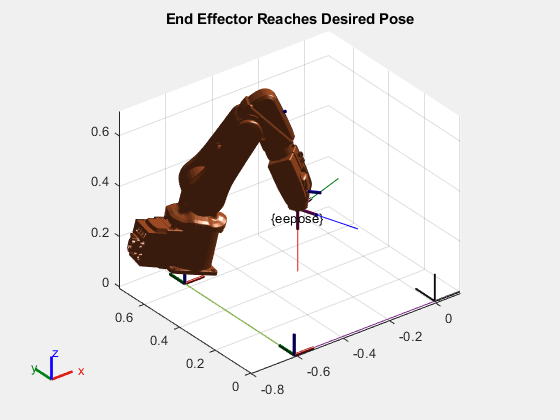

Matlab 复制代码

[v1,v2] = view

v1 = 
-37.5000
v2 = 
30

逆运动学解法可使机器人实现所需的末端执行器姿势，但由于底座的旋转不受制约，因此底座可以有任何方向。显示求解关节构型中浮动底座的方向。请注意，浮动底座的方向不为零。

Matlab 复制代码

disp(qsoln(4:6))

   -0.0005    0.2667   -0.2702

如果基座可以自由移动，那么这个问题就有无数个解决方案。如果基座姿态已知，而所需的末端执行器姿态可以达到，那么就有可能找到满足所需末端执行器姿态的唯一真实关节构型。另一种方法是对基本姿态进行约束，根据系统要求指定位置和方向约束。例如，在只允许底座平移的龙门系统中，必须对浮动底座的方向进行约束。

四、求解受约束浮动基座的 IK

要约束浮动底座的方向，可设置关节的关节位置限制（JointPositionLimits）属性，将其在世界坐标系中绕 x、y 和 z 轴的旋转限制为接近于零。逆运动学求解器要求零的公差值很小，以避免出现运动学奇点。因此，与其将关节限值设置为 [0 0]，不如将关节限值设置为非零的最小双精度值 [-eps eps]。

Matlab 复制代码

fb = getBody(floatingABBIrb,"floating_base_RX");
fb.Joint.PositionLimits = [-eps eps];
fb = getBody(floatingABBIrb,"floating_base_RY");
fb.Joint.PositionLimits = [-eps eps];
fb = getBody(floatingABBIrb,"floating_base_RZ");
fb.Joint.PositionLimits = [-eps eps];

为该刚体树重新创建逆运动学求解器，并求解关节构型。

Matlab 复制代码

ik = inverseKinematics(RigidBodyTree=floatingABBIrb);
[qsoln,solninfo] = ik(eename,eepose.tform,ones(1,6),homeConfiguration(floatingABBIrb));

请注意，逆运动学求解器成功找到了一个几乎没有底座方向的关节构型。

显示求解器的成功状态和浮动基座的方向。

Matlab 复制代码

disp(solninfo.Status)

success

Matlab 复制代码

disp(qsoln(4:6)) 

   1.0e-15 *

    0.2220    0.2220   -0.2220

可视化关节构型解决方案。请注意，在浮动基座旋转受限的情况下，机器人达到了预期姿态。

Matlab 复制代码

figure
plotTransforms(eepose,FrameSize=0.25,FrameLabel="eepose");
hold on
show(floatingABBIrb,qsoln);
hold off
title(["Robot Reaches Desired Pose with","Constrained Floating Base Rotation"])
view([v1 v2])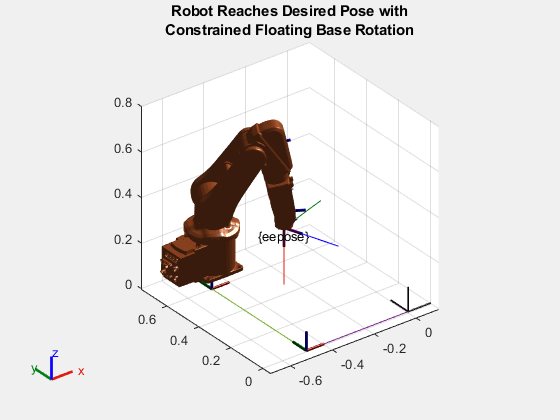

五、解决指定基座姿态的 IK 问题

如前所述，浮动基座系统的 IK 问题有无数种解决方案，因为基座可以在任何地方，而且对于每个基座姿态，都可能存在满足末端执行器姿态的机械臂关节构型。如果基座姿态固定且已知，另一种方法是在指定基座姿态下求解关节构型。本质上是将浮动基座视为固定基座。

首先，从机械臂的原始基座开始，获取浮动基座系统的机械臂子树。然后为该子树创建 IK 求解器。

Matlab 复制代码

fixedBaseTree = subtree(floatingABBIrb,abbirb.BaseName);
ikFixedBaseTree = inverseKinematics("RigidBodyTree",fixedBaseTree);

指定基座位于 xyz 位置 [-0.2 0.2 0.3]，相对于世界坐标系的欧拉 XYZ 方向为 [0.0 0.0 pi]。

Matlab 复制代码

basePosition = [0.3 0.3 0.1];
baseEulXYZ = [0 0 pi]; %[-pi/4 0.0 -pi/3];

由于逆运动学（inverseKinematics）函数计算的是末端执行器姿态相对于刚体树固定基座的关节值，因此在计算 IK 解决方案之前，必须将末端执行器姿态转换为基座坐标系。

Matlab 复制代码

eePoseWrtFixedBase = se3(baseEulXYZ,"eul","XYZ",basePosition)\eepose;

将关节位置 qjoint 与给定的固定基座位置和基座方向结合起来进行可视化，以验证末端执行器是否达到所需的姿势。

Matlab 复制代码

plotTransforms(eepose,FrameLabel="eepose",FrameSize=0.25);
hold on
[qjoint,solninfo] = ikFixedBaseTree(eename,eePoseWrtFixedBase.tform,ones(1,6),homeConfiguration(fixedBaseTree));
show(floatingABBIrb,[basePosition,baseEulXYZ,qjoint]);
title(["Robot Reaches Desired Pose","with Specified Base Pose"])
view([v1,v2])
hold off

请注意，IK 求解器能够找到解决方案。

Matlab 复制代码

disp(solninfo.Status)

success