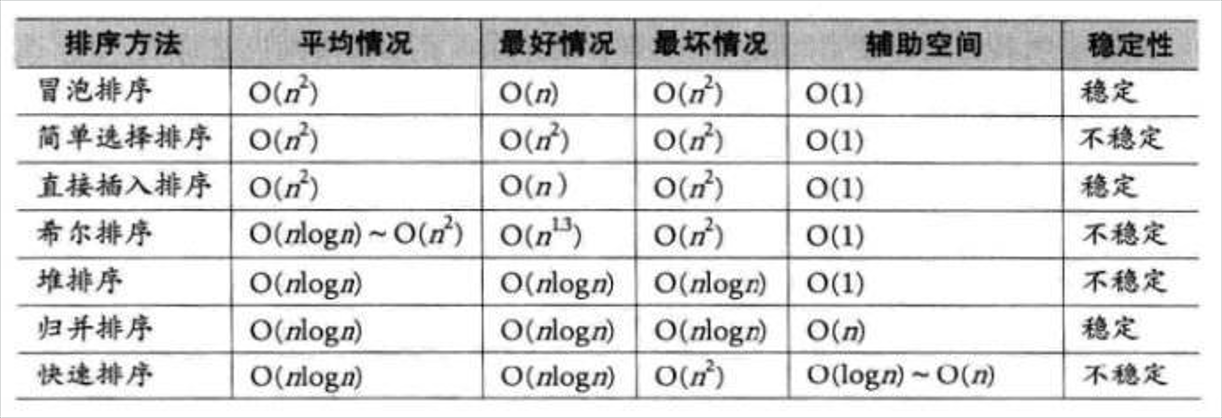
基数排序
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机上的贡献[1]。基数排序算法早在1923年被广泛运用在打孔卡的排序。
它是一种典型的非比较型排序算法,所含的算法思想同计数排序有所相似,同时它也不仅可以被用于整数,
算法思想
它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
它使用桶来对同一位数的不同大小进行分装,首先进行个位数的排序存放,再进行十位数的排序存放,然后是百位数...我们可以通过取出最大值来确定最高位数,从而确定需要进行几轮的排序存放操作。
基数排序的方式可以采用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
图解
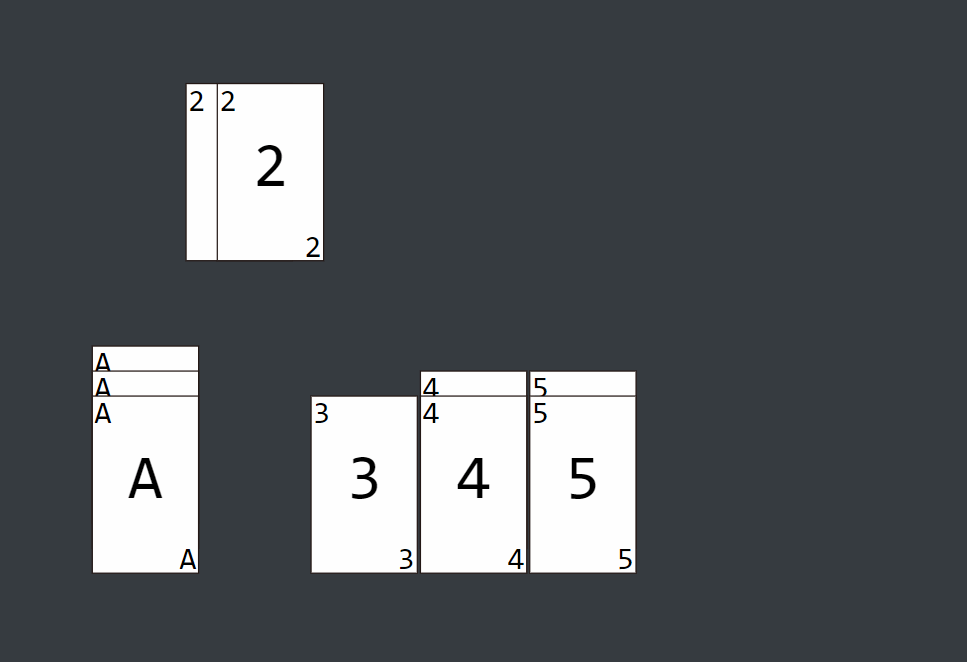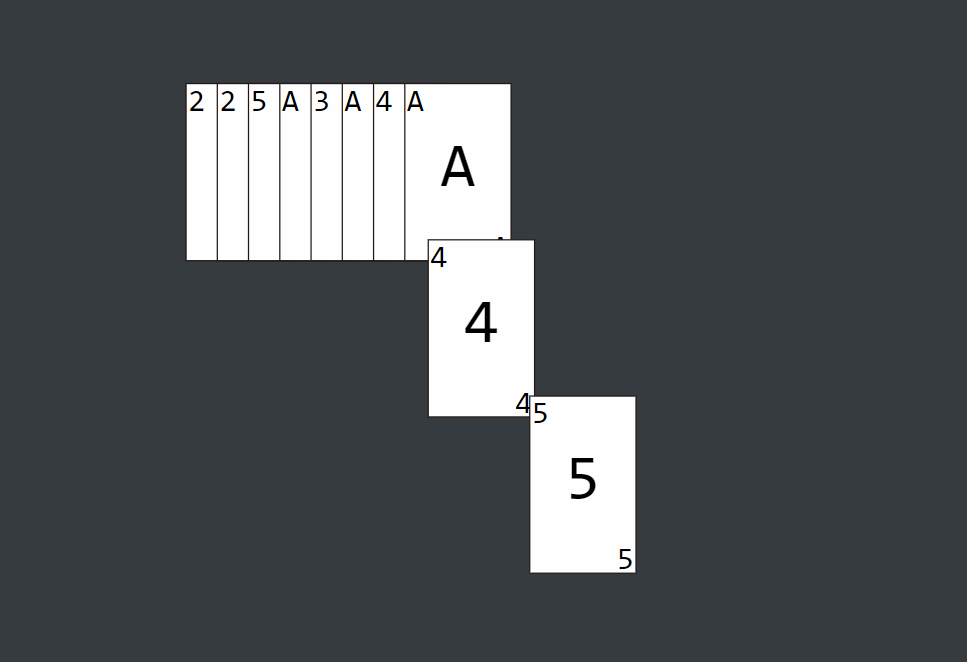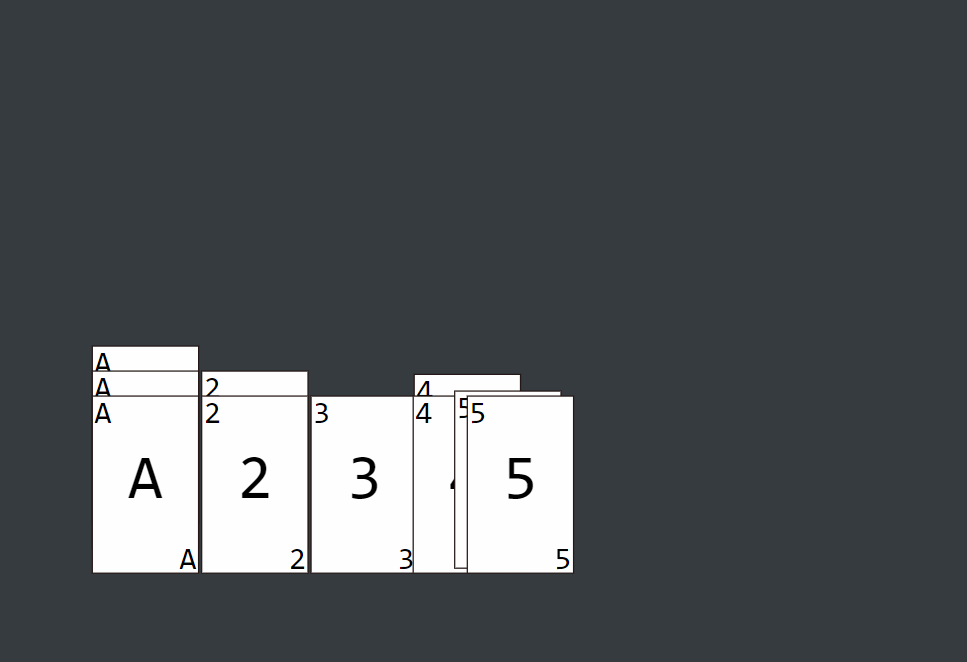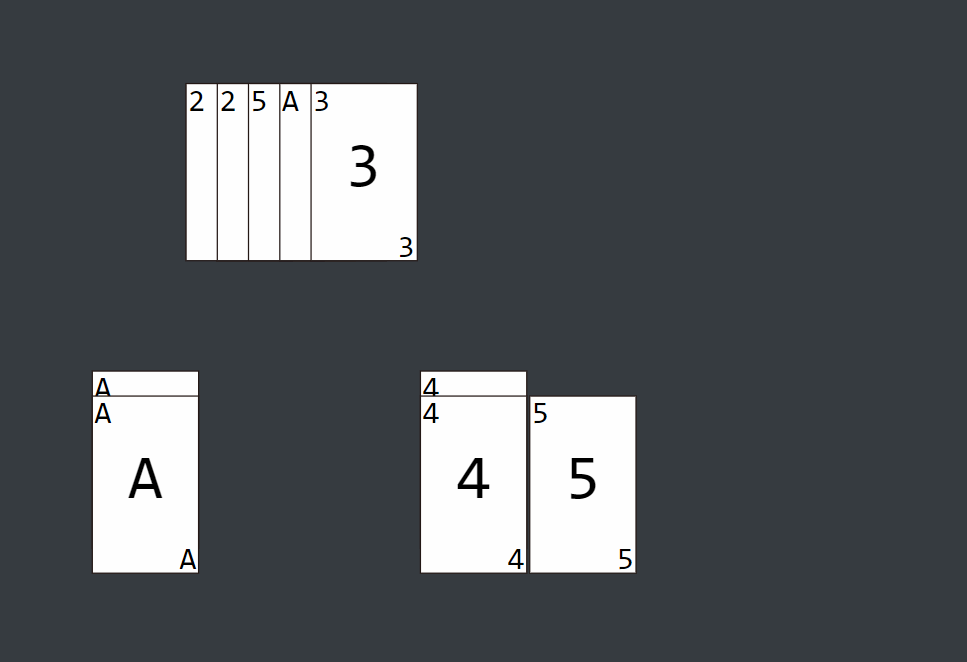
代码分析
(注:本段摘自网络,因为觉得写得很好!)
c++
#include<iostream>
#include<stdlib.h>
using namespace std;
void Radixsort(int a[], int length)//基数排序
{
int max = a[0], base = 1;//base与max用来判断进行几趟排序
for (int i = 1; i < length; i++)
{
if (max < a[i]) max = a[i];
}
int* t = (int*)malloc(sizeof(int) * length);//用t数组临时储存每一趟排好的结果
while (max / base > 0)//最大数为n位数就进行n次
{
int bucket[10] = { 0 };
for (int i = 0; i < length; i++)//统计每个桶中的数目
bucket[a[i] / base % 10]++;
for (int i = 1; i < length; i++)//将各个桶中的数目相加
bucket[i] += bucket[i - 1];
for (int i = length - 1; i >= 0; i--)//将数据依次放入桶中
{
t[bucket[a[i] / base % 10] - 1] = a[i];
bucket[a[i] / base % 10]--;
}
for (int i = 0; i < length; i++)//将排好的数据放回a数组中
a[i] = t[i];
base = base * 10;
}
}我们需要分析一下这段代码:
- 第一个for
c++
for(int i=0;i<length;i++)
bucket[a[i]/base%10]++;这里是算出每个桶内有几个数,bucket[i]代表i号桶内有bucket[i]个数。
- 第二个for
c++
for(int i=1;i<10;i++)
bucket[i]+=bucket[i-1];- 第三个for
c++
for(int i=length-1;i>=0;i--)
{t[bucket[a[i]/base%10]-1]=a[i];
bucket[a[i]/base%10]--;} bucket[a[i]/base%10]就是看a[i]在哪个桶内;-1是观察到在x号桶内的数据要存入t数组的话在t数组的下标是bucket[x]-1;
另一个要注意的是这里是从最后一个数开始存,是因为同一个桶里如果有两个数字 ,那么下面的一个数字在原序列中一定排在上面那个数字的后面,不能够重合。收集的时候如果从前往后收集,就是先收集上面的数字,存放的位置下标不好计算,并不知道桶里有几个数字。
MSD 基数排序
基于 k - 关键字元素的比较方法,可以想到:先比较所有元素的第1关键字,就可以确定出各元素大致的大小关系;然后对 具有相同第1关键字的元素,再比较它们的第2关键字......以此类推。
由于是从第1关键字到第k关键字顺序进行比较,由上述思想导出的排序算法称为 MSD(Most Significant Digit first)基数排序。
LSD 基数排序
MSD 基数排序从第1关键字到第k关键字顺序进行比较,为此需要借助递归或迭代来实现,时间常数还是较大,而且在比较自然数上还是略显不便。
而将递归的操作反过来:从第k关键字到第1关键字顺序进行比较,就可以得到 LSD(Least Significant Digit first)基数排序,不使用递归就可以完成的排序算法。
时间复杂度
基数排序的时间复杂度可以看成是:O(k*n),n是排序元素的个数,k是位数。这个复杂度往往是优于O(nlogn)的;k的大小决定了要进行的轮数,n是每轮要处理的个数。
基数排序是否比基于比较的排序算法(如快速排序)更好呢?通常情况要比快速排序的期望运行时间代价更好一些。但是,在处理的n个关键字时,尽管基数排序执行的循环轮数会比快速排序要少,但每一轮它所耗费的时间要长得多 。哪一个排序算法更合适依赖于具体实现和底层硬件的特性 (例如,快速排序通常可以比基数排序更有效地使用硬件的缓存),以及输人数据的特征。此外,利用计数排序作为中间稳定排序的基数排序不是原址排序 ,而很多O(nlogn)时间的比较排序是原址排序。因此,当主存的容量比较宝贵时,我们可能会更倾向于像快速排序这样的原址排序算法。
稳定性
如果对内层关键字的排序是稳定的,则 MSD 基数排序和 LSD 基数排序都是稳定的排序算法。