[LeetCode] 1162. 地图分析

题目描述：

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

复制代码

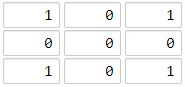
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

复制代码

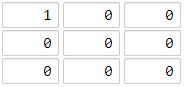
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 不是 0 就是 1

题目链接：

. - 力扣（LeetCode）

解题主要思路：

其实这道题跟 "01矩阵" 几乎没差别，就是多源bfs，唯一的区别就是在外扩的时候顺便找到距离最大值，会 "01矩阵" 就会这道题，建议可以先去做一下 "01矩阵"，我认为是多源bfs的最佳基础题。

01矩阵链接：

$LeetCode$ 542. 01矩阵-CSDN博客

解题代码：；

cpp 复制代码

class Solution {
public:
    int dx[4]{0, 0, 1, -1};
    int dy[4]{1, -1, 0, 0};
    int maxDistance(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> ret(m, vector(n, -1));
        queue<pair<int, int>> que;
        // 将所有陆地入队列
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) { 
                    ret[i][j] = 0;
                    que.push(make_pair(i, j));
                }
            }
        }
        int max_dis = -1;
        // 一层一层往外扩
        while (que.size()) {
            auto [a, b] = que.front();
            que.pop();
            for (int i = 0; i < 4; ++i) {
                int x = a + dx[i], y = b + dy[i];
                if (x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1) {
                    ret[x][y] = ret[a][b] + 1;
                    max_dis = max(max_dis, ret[x][y]);
                    que.push(make_pair(x, y));
                }
            }
        }
        return max_dis;
    }
};