时间序列预测（九）——门控循环单元网络（GRU）

目录

一、GRU结构

二、GRU核心思想

[1、更新门（Update Gate）：决定了当前时刻隐藏状态中旧状态和新候选状态的混合比例。](#1、更新门（Update Gate）：决定了当前时刻隐藏状态中旧状态和新候选状态的混合比例。)

[2、重置门（Reset Gate）：用于控制前一时刻隐藏状态对当前候选隐藏状态的影响程度。](#2、重置门（Reset Gate）：用于控制前一时刻隐藏状态对当前候选隐藏状态的影响程度。)

[3、候选隐藏状态（Candidate Hidden State）：生成当前隐藏状态的候选值](#3、候选隐藏状态（Candidate Hidden State）：生成当前隐藏状态的候选值)

[三、GRU 分步演练](#三、GRU 分步演练)

1、输入与初始化：

2、计算重置门：

3、计算候选隐藏状态：

4、计算更新门：

5、计算当前隐藏状态：

四、代码实现

1、任务:

2、做法：

3、主要修改点：

4、具体代码：

5、结果

---

GRU是一种循环神经网络（RNN）的变体，由Cho等人在2014年提出。相比于传统的RNN，GRU引入了门控机制，可以通过该机制来确定应该何时更新隐状态，以及应该何时重置隐状态，使得网络能够更好地捕捉长期依赖性，同时减少了梯度消失的问题。

一、GRU结构

GRU的结构和基础的RNN相比，并没有特别大的不同，都是一种重复神经网络模块的链式结构， 由输入层、隐藏层和输出层组成，其中隐藏层是其核心部分，包含了门控机制相关的计算单元**。**

二、GRU核心思想

与LSTM不同，GRU没有细胞状态，而是直接使用隐藏状态。GRU由两个门控制：更新门（Update Gate）和重置门（Reset Gate）。

1、更新门（Update Gate）：决定了当前时刻隐藏状态中旧状态和新候选状态的混合比例。

**2、重置门（Reset Gate）：**用于控制前一时刻隐藏状态对当前候选隐藏状态的影响程度。

补充：

3、候选隐藏状态（Candidate Hidden State）：生成当前隐藏状态的候选值

三、GRU 分步演练

1、输入与初始化：

• 假设我们有一个输入序列 X=[x1,x2,...,xT]，其中 xt 是第 t 个时间步的输入。
• 初始化隐藏状态 h0，通常为零向量或随机初始化。

2、计算重置门：

• 重置门 rt 决定了前一时间步的隐藏状态 ht−1 对当前候选隐藏状态 h~t 的影响程度。 其中 σ 是sigmoid函数，Wr 和 Ur 是可训练的权重矩阵。

3、计算候选隐藏状态：

• 使用重置门 rt 来控制前一时间步的隐藏状态 ht−1 的影响。 其中 ⊙ 表示元素乘法，tanh 是双曲正切函数，W 和 U 是可训练的权重矩阵。

4、计算更新门：

• 更新门 zt 决定了当前隐藏状态 ht 应该保留多少前一时间步的隐藏状态 ht−1 和多少当前候选隐藏状态 h~t。 其中 Wz 和 Uz 是可训练的权重矩阵。

5、计算当前隐藏状态：

• 使用更新门 zt 来组合前一时间步的隐藏状态 ht−1 和当前候选隐藏状态 h~t。

四、代码实现

1、任务:

根据一个包含道路曲率（Curvature）、车速（Velocity）、侧向加速度（Ay）和方向盘转角（Steering_Angle）真实的数据集，去预测未来的方向盘转角。

2、做法：

提取前5个历史曲率、速度、方向盘转角作为输入特征，同时添加后5个未来曲率（由于车辆的预瞄距离）。目标输出为未来5个方向盘转角。采用GRU网络训练。

3、主要修改点：

1. 模型定义 ：将 LSTM 替换为 GRU，并更新模型类名为 GRUModel。
2. 前向传播 ：forward 方法中相应地使用 GRU 的输出。

4、具体代码：

# GRU 模型
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error as mae, r2_score
import matplotlib.pyplot as plt

# 1. 数据预处理
# 读取数据
data = pd.read_excel('input_data_20241010160240.xlsx')  # 替换为你的数据文件路径  

# 提取特征和标签
curvature = data['Curvature'].values
velocity = data['Velocity'].values
steering = data['Steering_Angle'].values

# 定义历史和未来的窗口大小
history_size = 5
future_size = 5

features = []
labels = []
for i in range(history_size, len(data) - future_size):
    # 提取前5个历史的曲率、速度和方向盘转角
    history_curvature = curvature[i - history_size:i]
    history_velocity = velocity[i - history_size:i]
    history_steering = steering[i - history_size:i]

    # 提取后5个未来的曲率（用于预测）
    future_curvature = curvature[i:i + future_size]

    # 输入特征：历史 + 未来曲率
    feature = np.hstack((history_curvature, history_velocity, history_steering, future_curvature))
    features.append(feature)

    # 输出标签：未来5个方向盘转角
    label = steering[i:i + future_size]
    labels.append(label)

# 转换为 NumPy 数组
features = np.array(features)
labels = np.array(labels)

# 归一化
scaler_x = StandardScaler()
scaler_y = StandardScaler()

features = scaler_x.fit_transform(features)
labels = scaler_y.fit_transform(labels)

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(features, labels, test_size=0.05)

# 将特征转换为三维张量，形状为 [样本数, 时间序列长度, 特征数]
input_feature_size = history_size * 3 + future_size  # 历史曲率、速度、方向盘转角 + 未来曲率
x_train_tensor = torch.tensor(x_train, dtype=torch.float32).view(-1, 1, input_feature_size)  # [batch_size, seq_len=1, input_size]
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).view(-1, future_size)  # 输出未来的5个方向盘转角
x_test_tensor = torch.tensor(x_test, dtype=torch.float32).view(-1, 1, input_feature_size)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32).view(-1, future_size)

# 2. 创建GRU模型
class GRUModel(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, output_size):
        super(GRUModel, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.gru = nn.GRU(input_size, hidden_size, num_layers, batch_first=True)  # 使用GRU
        self.fc = nn.Linear(hidden_size, output_size)  # 输出层

    def forward(self, x):
        # 前向传播
        out, _ = self.gru(x)  # GRU输出
        out = self.fc(out[:, -1, :])  # 只取最后一个时间步的输出
        return out

# 实例化模型
input_size = input_feature_size  # 输入特征数
hidden_size = 64  # 隐藏层大小
num_layers = 2  # GRU层数
output_size = future_size  # 输出5个未来方向盘转角
model = GRUModel(input_size, hidden_size, num_layers, output_size)

# 3. 设置损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 4. 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()
    
    # 前向传播
    outputs = model(x_train_tensor)
    loss = criterion(outputs, y_train_tensor)

    # 后向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# 5. 预测
model.eval()
with torch.no_grad():
    y_pred_tensor = model(x_test_tensor)

y_pred = scaler_y.inverse_transform(y_pred_tensor.numpy())  # 将预测值逆归一化
y_test = scaler_y.inverse_transform(y_test_tensor.numpy())  # 逆归一化真实值

# 评估指标
r2 = r2_score(y_test, y_pred, multioutput='uniform_average')  # 多维输出下的R^2
mae_score = mae(y_test, y_pred)
print(f"R^2 score: {r2:.4f}")
print(f"MAE: {mae_score:.4f}")

# 支持中文
plt.rcParams['font.sans-serif'] = ['SimSun']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 绘制未来5个方向盘转角的预测和真实值对比
plt.figure(figsize=(10, 6))
for i in range(future_size):
    plt.plot(range(len(y_test)), y_test[:, i], label=f'真实值 {i+1} 步', color='blue')
    plt.plot(range(len(y_pred)), y_pred[:, i], label=f'预测值 {i+1} 步', color='red')
plt.xlabel('样本索引')
plt.ylabel('Steering Angle')
plt.title('未来5个方向盘转角的实际值与预测值对比图')
plt.legend()
plt.grid(True)
plt.show()

# 计算预测和真实方向盘转角的平均值
y_pred_mean = np.mean(y_pred, axis=1)  # 每个样本的5个预测值取平均
y_test_mean = np.mean(y_test, axis=1)  # 每个样本的5个真实值取平均

# 绘制平均值的实际值与预测值对比图
plt.figure(figsize=(10, 6))
plt.plot(range(len(y_test_mean)), y_test_mean, label='真实值（平均）', color='blue')
plt.plot(range(len(y_pred_mean)), y_pred_mean, label='预测值（平均）', color='red')
plt.xlabel('样本索引')
plt.ylabel('Steering Angle (平均)')
plt.title('未来5个方向盘转角的平均值对比图')
plt.legend()
plt.grid(True)
plt.show()

# 绘制第1个时间步的实际值与预测值对比图
plt.figure(figsize=(10, 6))
plt.plot(range(len(y_test)), y_test[:, 0], label='真实值 (第1步)', color='blue')
plt.plot(range(len(y_pred)), y_pred[:, 0], label='预测值 (第1步)', color='red')
plt.xlabel('样本索引')
plt.ylabel('Steering Angle')
plt.title('未来第1步方向盘转角的实际值与预测值对比图')
plt.legend()
plt.grid(True)
plt.show()

# 计算每个时间步的平均绝对误差
time_steps = y_test.shape[1]
mae_per_step = [mae(y_test[:, i], y_pred[:, i]) for i in range(time_steps)]

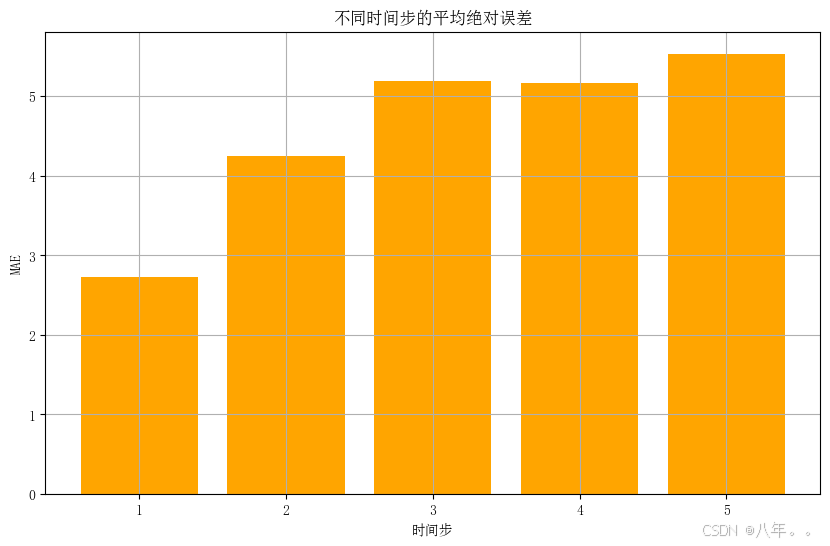
# 绘制每个时间步的平均绝对误差
plt.figure(figsize=(10, 6))
plt.bar(range(1, time_steps + 1), mae_per_step, color='orange')
plt.xlabel('时间步')
plt.ylabel('MAE')
plt.title('不同时间步的平均绝对误差')
plt.grid(True)
plt.show()

5、结果

五、总结

GRU是LSTM的简化版本，减少了门的数量，使得训练和推理速度更快。它在许多序列建模任务中表现良好，适用于时间序列预测、自然语言处理等领域。