在深度学习的领域中,前向传播、反向传播和损失函数是构建和训练神经网络模型的三个核心概念。今天,小编将通过一个简单的实例,解释这三个概念,并展示它们的作用。
前向传播:神经网络的"思考"过程
前向传播是神经网络计算的基础步骤,它涉及将输入数据逐层传递,通过神经网络的权重和激活函数,最终输出预测结果。这个过程包含**"样本数据输入、算法模型、输出"**这几个步骤。
我们来举个简单的例子,比如给一个小宝宝看一张图片,然后问他:"这上面画的是什么?"他就会用他的小脑袋瓜去"思考"这张图片,然后告诉你答案。前向传播就像是这个过程,只不过小宝宝换成了神经网络。
- 样本数据输入:这一步将图像、文字、语音等样本数据转换为我们电脑能识别的数字输入。就像小宝宝看到图片,神经网络也接收到一张图片,这张图片被转换成一串数字。
- 算法模型:简单来说,就是一些数学计算,主要包含线性层+规则化层+激活,线性层负责做线性函数的拟合;规则化层负责把我们的线性拟合规则化,方便后面的计算;激活层负责的是变成非线性化,因为我们的现实世界是非线性的。所以整个过程就是:我们输入的样本是非线性的,我们通过这样一堆数学公式,去拟合非线性的样本数据。
- 输出层:也是一些数学运算,比如Linear或者Conv,负责将模型的输出转换为预测结果输出。
这个过程可以用下面的数学公式表示:

损失函数:告诉神经网络它错了多少
损失函数是衡量模型预测结果与真实标签之间差距的依据,它的核心作用是告诉我们模型的预测结果"错"得有多离谱。通俗来说,损失函数就像是一个裁判,它给模型的预测结果打分,分数越低,说明模型的预测结果越接近真实情况,模型的性能就越好。损失函数是为了让我们反向传播起作用的。就像如果小宝宝猜错了,你会告诉他:"不对哦,这是数字8,不是3。"损失函数就像是这句话,它告诉神经网络:"嘿,你的答案有点偏差。"
下面是几种常用的损失函数:
L1 Loss(MAE) :平均绝对误差,对异常值的容忍性更高,但当梯度下降恰好为0时无法继续进行。就像是你告诉小宝宝:"你的答案差了多远。"这个距离就是损失值。
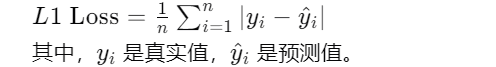
L2 Loss(MSE) :均方误差,连续光滑,方便求导,但易受到异常值的干扰。这就像是你告诉小宝宝:"你的答案差了多少个单位。"这个单位的平方和就是损失值。
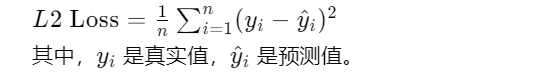
Smooth L1 Loss :处理异常值更加稳健,同时避免了L2 Loss的梯度爆炸问题。就像是你告诉小宝宝:"你的答案差了多远,但我不会因为你猜得特别离谱就惩罚你。"这个损失函数对极端错误更宽容。

反向传播:神经网络的"自我修正"过程
反向传播是利用损失函数的梯度来更新网络参数的过程。它从输出层开始,逆向通过网络,利用链式法则计算每个参数对损失函数的梯度。包含这几个过程:
- 计算输出层误差梯度:首先计算输出层的误差梯度,这是损失函数对输出层权重的敏感度。
- 逐层反向传播:然后从输出层开始,逆向通过网络,逐层计算误差梯度。
- 更新权重和偏置:使用梯度下降算法,根据计算出的梯度更新网络中每一层的权重和偏置。
所以前向传播、反向传播、损失函数之间的关系是这样的:
他们都是深度学习训练过程中的核心。前向传播 负责生成预测结果,损失函数 负责量化预测结果与真实标签之间的差异,而反向传播则负责利用这些差异来更新模型参数,以减少损失函数的值。
通过三者的结合,我们可以构建、训练并优化深度学习模型,使其能够从数据中学习复杂的模式,并在各种任务如图像识别、自然语言处理和预测分析中做出准确的预测。
前向传播、反向传播、损失函数属于机器学习领域中的核心概念,在AI全体系课程中,是理解其他更复杂机器学习算法的基础,掌握这几个概念对于深入学习机器学习、理解更高级的算法以及在实际应用中设计和优化模型都具有重要的意义。通过理解前向传播、反向传播和损失函数,学习者能够更好地把握机器学习模型的工作原理,为进一步探索深度学习和其他高级机器学习技术打下坚实的基础。