代码随想录算法训练营第五十八天|Day58 图论

拓扑排序精讲

https://www.programmercarl.com/kamacoder/0117.%E8%BD%AF%E4%BB%B6%E6%9E%84%E5%BB%BA.html

拓扑排序的背景

本题是拓扑排序的经典题目。

一聊到拓扑排序，一些录友可能会想这是排序，不会想到这是图论算法。

其实拓扑排序是经典的图论问题。

先说说拓扑排序的应用场景。

大学排课，例如先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序。问给规划出一条完整的上课顺序。

拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。

如果给出一条线性的依赖顺序来下载这些文件呢？

有录友想上面的例子都很简单啊，我一眼能给排序出来。

那如果上面的依赖关系是一百对呢，一千对甚至上万个依赖关系，这些依赖关系中可能还有循环依赖，你如何发现循环依赖呢，又如果排出线性顺序呢。

所以拓扑排序就是专门解决这类问题的。

概括来说，给出一个有向图，把这个有向图转成线性的排序就叫拓扑排序。

当然拓扑排序也要检测这个有向图是否有环，即存在循环依赖的情况，因为这种情况是不能做线性排序的。

所以拓扑排序也是图论中判断有向无环图的常用方法。

#拓扑排序的思路

拓扑排序指的是一种解决问题的大体思路，而具体算法，可能是广搜也可能是深搜。

大家可能发现各式各样的解法，纠结哪个是拓扑排序？

其实只要能在把有向无环图进行线性排序的算法都可以叫做拓扑排序。

实现拓扑排序的算法有两种：卡恩算法（BFS）和DFS

卡恩1962年提出这种解决拓扑排序的思路

一般来说我们只需要掌握 BFS （广度优先搜索）就可以了，清晰易懂，如果还想多了解一些，可以再去学一下 DFS 的思路，但 DFS 不是本篇重点。

接下来我们来讲解BFS的实现思路。

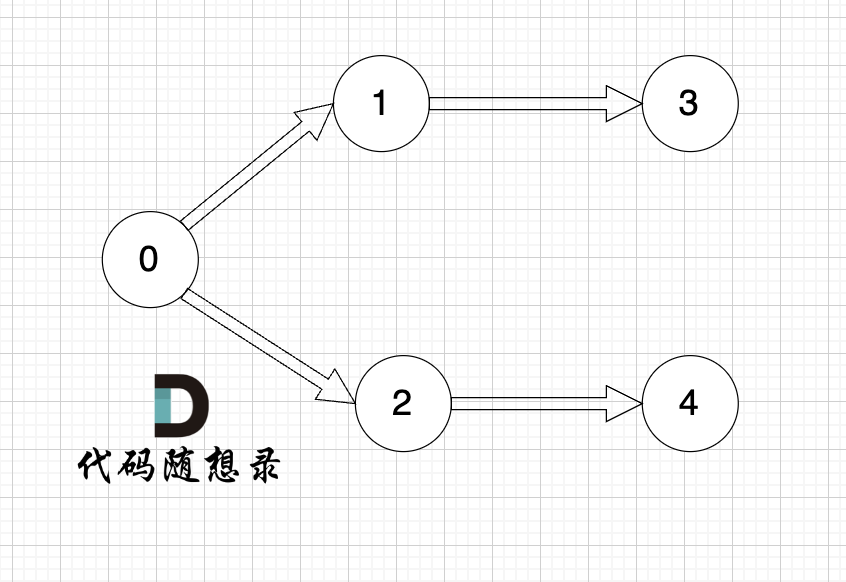
以题目中示例为例如图：

做拓扑排序的话，如果肉眼去找开头的节点，一定能找到节点0 吧，都知道要从节点0 开始。

但为什么我们能找到节点0呢，因为我们肉眼看着这个图就是从节点0出发的。

作为出发节点，它有什么特征？

你看节点0 的入度为0 出度为2，也就是没有边指向它，而它有两条边是指出去的。

节点的入度表示有多少条边指向它，节点的出度表示有多少条边从该节点出发。

所以当我们做拓扑排序的时候，应该优先找入度为 0 的节点，只有入度为0，它才是出发节点。 理解以上内容很重要！

接下来我给出拓扑排序的过程，其实就两步：

找到入度为0 的节点，加入结果集

将该节点从图中移除

循环以上两步，直到所有节点都在图中被移除了。

结果集的顺序，就是我们想要的拓扑排序顺序（结果集里顺序可能不唯一）

#模拟过程

用本题的示例来模拟这一过程：

1、找到入度为0 的节点，加入结果集

2、将该节点从图中移除

1、找到入度为0 的节点，加入结果集

这里大家会发现，节点1 和节点2 入度都为0，选哪个呢？

选哪个都行，所以这也是为什么拓扑排序的结果是不唯一的。

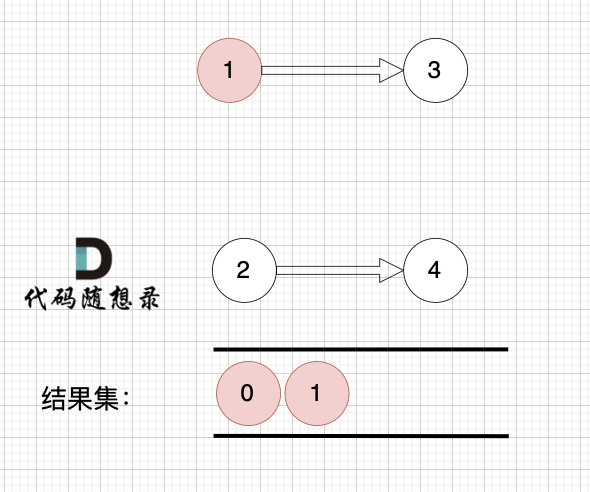
2、将该节点从图中移除

1、找到入度为0 的节点，加入结果集

节点2 和节点3 入度都为0，选哪个都行，这里选节点2

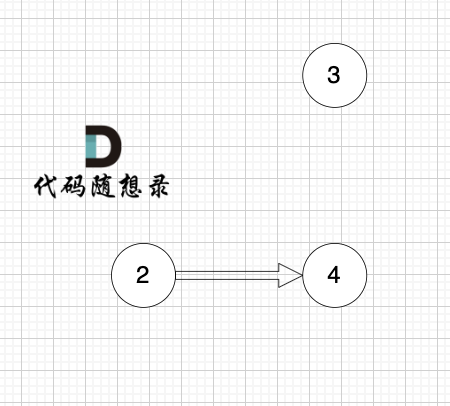
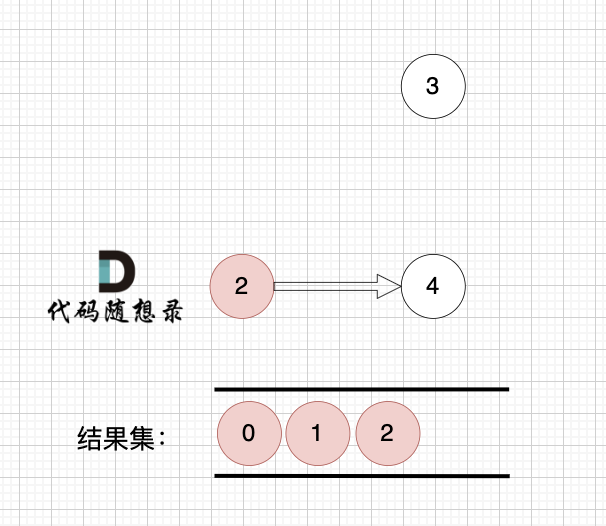
2、将该节点从图中移除

后面的过程一样的，节点3 和节点4，入度都为0，选哪个都行。

最后结果集为： 0 1 2 3 4 。当然结果不唯一的。

#判断有环

如果有有向环怎么办呢？例如这个图：

这个图，我们只能将入度为0 的节点0 接入结果集。

之后，节点1、2、3、4 形成了环，找不到入度为0 的节点了，所以此时结果集里只有一个元素。

那么如果我们发现结果集元素个数不等于图中节点个数，我们就可以认定图中一定有有向环！

这也是拓扑排序判断有向环的方法。

通过以上过程的模拟大家会发现这个拓扑排序好像不难，还有点简单。

思路

objectivec 复制代码

#include <stdio.h>
#include <stdlib.h>

#define MAXN 1000 // 假设最大文件数为1000

typedef struct {
    int *data;
    int front, rear, size, capacity;
} Queue;

// 创建队列的函数
Queue* createQueue(int capacity) {
    Queue* queue = (Queue*)malloc(sizeof(Queue));
    queue->capacity = capacity;
    queue->front = queue->size = 0;
    queue->rear = capacity - 1;
    queue->data = (int*)malloc(capacity * sizeof(int));
    return queue;
}

// 队列是否为空的函数
int isEmpty(Queue* queue) {
    return (queue->size == 0);
}

// 向队列添加元素的函数
void enqueue(Queue* queue, int item) {
    queue->rear = (queue->rear + 1) % queue->capacity;
    queue->data[queue->rear] = item;
    queue->size++;
}

// 从队列删除元素的函数
int dequeue(Queue* queue) {
    int item = queue->data[queue->front];
    queue->front = (queue->front + 1) % queue->capacity;
    queue->size--;
    return item;
}

// C语言版本的拓扑排序程序
int main() {
    int m, n, s, t;
    scanf("%d %d", &n, &m);
    
    int inDegree[MAXN] = {0}; // 记录每个文件的入度
    int adj[MAXN][MAXN] = {0}; // 记录依赖关系
    int outCount[MAXN] = {0}; // 每个节点的出度

    while (m--) {
        scanf("%d %d", &s, &t);
        inDegree[t]++;
        adj[s][outCount[s]++] = t; // 记录s指向哪些文件
    }

    Queue* que = createQueue(n); // 创建队列
    for (int i = 0; i < n; i++) {
        // 入度为0的文件，可以加入队列
        if (inDegree[i] == 0) {
            enqueue(que, i);
        }
    }

    int result[MAXN]; // 记录结果
    int count = 0;

    while (!isEmpty(que)) {
        int cur = dequeue(que); // 当前选中的文件
        result[count++] = cur;

        // 获取该文件指向的文件
        for (int i = 0; i < outCount[cur]; i++) {
            int next = adj[cur][i];
            inDegree[next]--;
            if (inDegree[next] == 0) {
                enqueue(que, next);
            }
        }
    }

    // 检查是否成功进行了拓扑排序
    if (count == n) {
        for (int i = 0; i < n - 1; i++) {
            printf("%d ", result[i]);
        }
        printf("%d\n", result[n - 1]);
    } else {
        printf("-1\n");
    }

    // 释放队列内存
    free(que->data);
    free(que);

    return 0;
}

学习反思

代码是一个C语言版本的拓扑排序程序。拓扑排序是一种根据一些有向无环图的依赖关系，对这些节点进行排序的算法。首先，程序读入了文件的个数n和依赖关系的条数m。然后，使用两个数组inDegree和adj来记录每个文件的入度和依赖关系。其中，inDegree[i]表示文件i的入度，adj[s][i]表示文件s依赖于文件i。接下来，程序创建了一个队列que来存储入度为0的文件。然后，遍历所有文件，将入度为0的文件加入到队列中。然后，程序使用一个循环，不断从队列中取出文件，并将其加入到结果数组result中。同时，程序将该文件指向的文件的入度减一，并将入度变为0的文件加入到队列中。最后，程序检查是否成功进行了拓扑排序。如果成功，输出排序结果；否则，输出-1。

dijkstra（朴素版）精讲

https://www.programmercarl.com/kamacoder/0047.%E5%8F%82%E4%BC%9Adijkstra%E6%9C%B4%E7%B4%A0.html

dijkstra算法：在有权图（权值非负数）中求从起点到其他节点的最短路径算法。

需要注意两点：

dijkstra 算法可以同时求起点到所有节点的最短路径

权值不能为负数

（这两点后面我们会讲到）

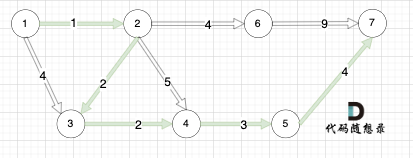
如本题示例中的图：

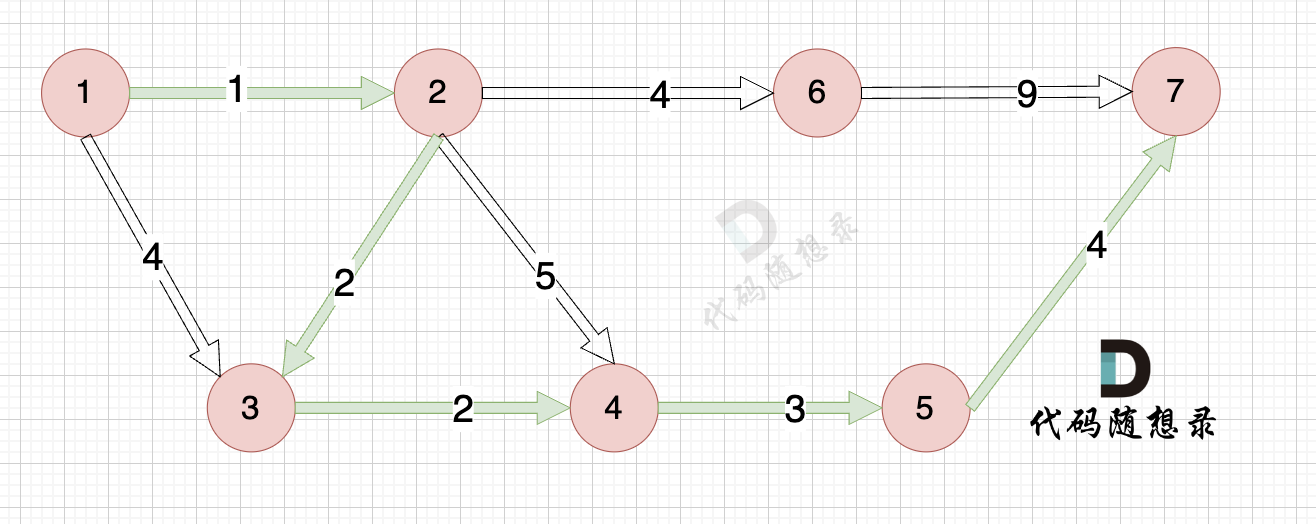
起点（节点1）到终点（节点7）的最短路径是图中标记绿线的部分。

最短路径的权值为12。

其实 dijkstra 算法和我们之前讲解的prim算法思路非常接近，如果大家认真学过prim算法，那么理解 Dijkstra 算法会相对容易很多。（这也是我要先讲prim再讲dijkstra的原因）

dijkstra 算法同样是贪心的思路，不断寻找距离源点最近的没有访问过的节点。

这里我也给出 dijkstra三部曲：

第一步，选源点到哪个节点近且该节点未被访问过

第二步，该最近节点被标记访问过

第三步，更新非访问节点到源点的距离（即更新minDist数组）

大家此时已经会发现，这和prim算法怎么这么像呢。

我在prim算法讲解中也给出了三部曲。 prim 和 dijkstra 确实很像，思路也是类似的，这一点我在后面还会详细来讲。

在dijkstra算法中，同样有一个数组很重要，起名为：minDist。

minDist数组用来记录每一个节点距离源点的最小距离。

理解这一点很重要，也是理解 dijkstra 算法的核心所在。

大家现在看着可能有点懵，不知道什么意思。

没关系，先让大家有一个印象，对理解后面讲解有帮助。

我们先来画图看一下 dijkstra 的工作过程，以本题示例为例：（以下为朴素版dijkstra的思路）

（示例中节点编号是从1开始，所以为了让大家看的不晕，minDist数组下标我也从 1 开始计数，下标0 就不使用了，这样下标和节点标号就可以对应上了，避免大家搞混）

#朴素版dijkstra

#模拟过程

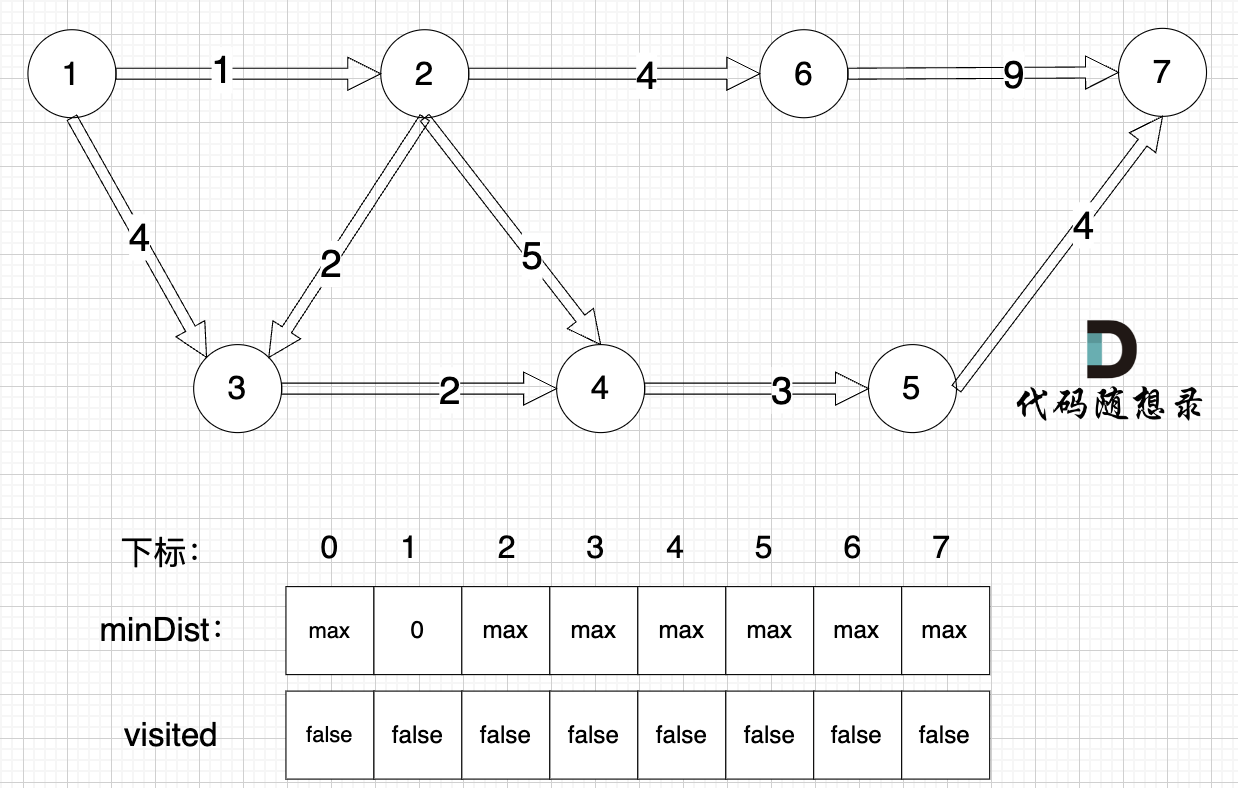
0、初始化

minDist数组数值初始化为int最大值。

这里在强点一下 minDist数组的含义：记录所有节点到源点的最短路径，那么初始化的时候就应该初始为最大值，这样才能在后续出现最短路径的时候及时更新。

（图中，max 表示默认值，节点0 不做处理，统一从下标1 开始计算，这样下标和节点数值统一，方便大家理解，避免搞混）

源点（节点1）到自己的距离为0，所以 minDist[1] = 0

此时所有节点都没有被访问过，所以 visited数组都为0

以下为dijkstra 三部曲

1、选源点到哪个节点近且该节点未被访问过

源点距离源点最近，距离为0，且未被访问。

2、该最近节点被标记访问过

标记源点访问过

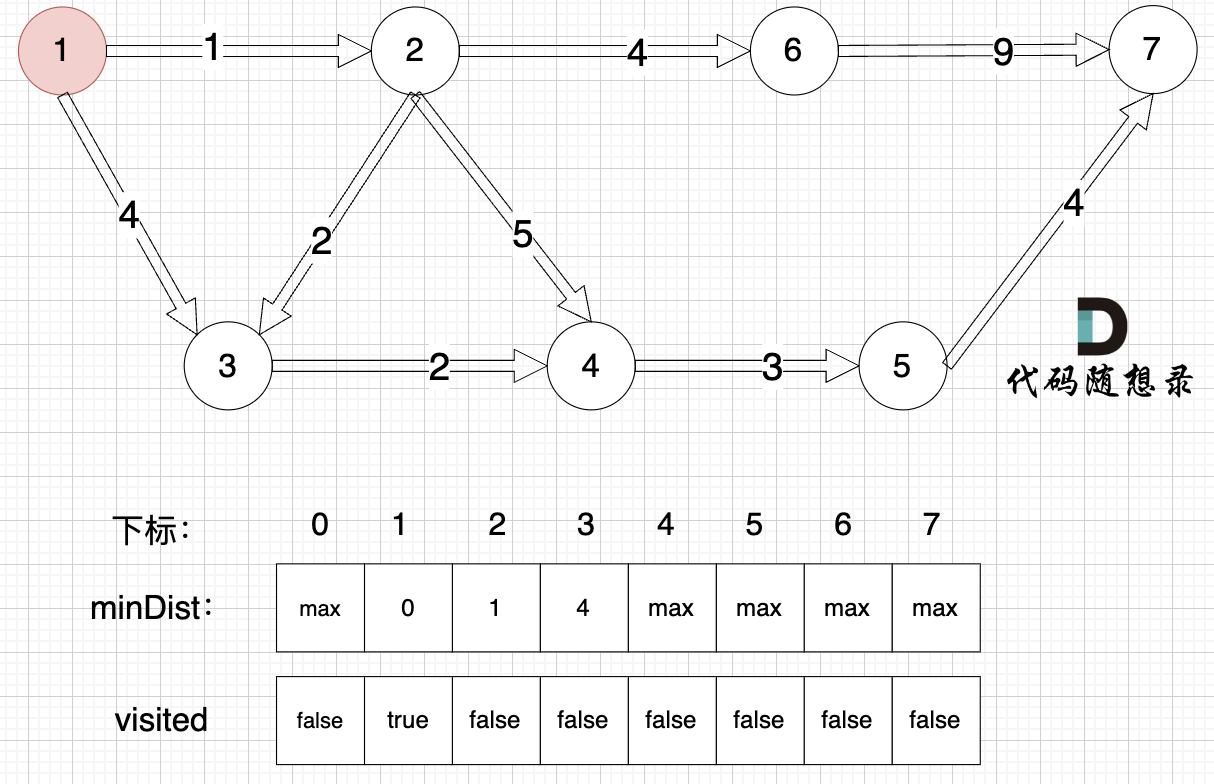
3、更新非访问节点到源点的距离（即更新minDist数组），如图：

更新 minDist数组，即：源点（节点1）到节点2 和节点3的距离。

源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1

源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4

可能有录友问：为啥和 minDist[2] 比较？

再强调一下 minDist[2] 的含义，它表示源点到节点2的最短距离，那么目前我们得到了源点到节点2的最短距离为1，小于默认值max，所以更新。 minDist[3]的更新同理

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点到节点2距离最近，选节点2

2、该最近节点被标记访问过

节点2被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组），如图：

更新 minDist数组，即：源点（节点1）到节点6 、节点3 和节点4的距离。

为什么更新这些节点呢？怎么不更新其他节点呢？

因为源点（节点1）通过已经计算过的节点（节点2）可以链接到的节点有节点3，节点4和节点6.

更新 minDist数组：

源点到节点6的最短距离为5，小于原minDist[6]的数值max，更新minDist[6] = 5

源点到节点3的最短距离为3，小于原minDist[3]的数值4，更新minDist[3] = 3

源点到节点4的最短距离为6，小于原minDist[4]的数值max，更新minDist[4] = 6

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点距离哪些节点最近，怎么算的？

其实就是看 minDist数组里的数值，minDist 记录了源点到所有节点的最近距离，结合visited数组筛选出未访问的节点就好。

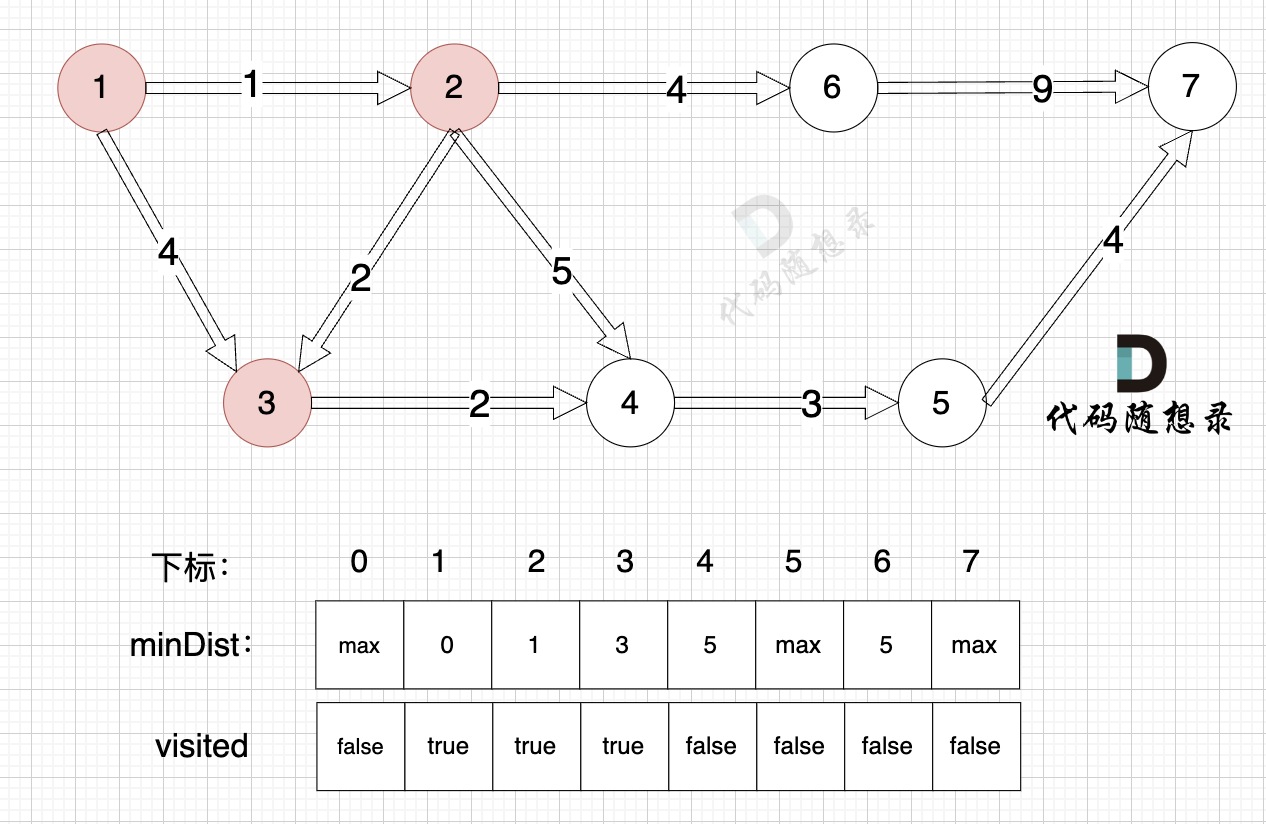
从上面的图，或者从minDist数组中，我们都能看出未访问过的节点中，源点（节点1）到节点3距离最近。

2、该最近节点被标记访问过

节点3被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组），如图：

由于节点3的加入，那么源点可以有新的路径链接到节点4 所以更新minDist数组：

更新 minDist数组：

源点到节点4的最短距离为5，小于原minDist[4]的数值6，更新minDist[4] = 5

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，有节点4 和节点6，距离源点距离都是 5 （minDist[4] = 5，minDist[6] = 5），选哪个节点都可以。

2、该最近节点被标记访问过

节点4被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组），如图：

由于节点4的加入，那么源点可以链接到节点5 所以更新minDist数组：

源点到节点5的最短距离为8，小于原minDist[5]的数值max，更新minDist[5] = 8

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点6，距离源点距离是 5 （minDist[6] = 5）

2、该最近节点被标记访问过

节点6 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组），如图：

由于节点6的加入，那么源点可以链接到节点7 所以更新minDist数组：

源点到节点7的最短距离为14，小于原minDist[7]的数值max，更新minDist[7] = 14

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点5，距离源点距离是 8 （minDist[5] = 8）

2、该最近节点被标记访问过

节点5 被标记访问过

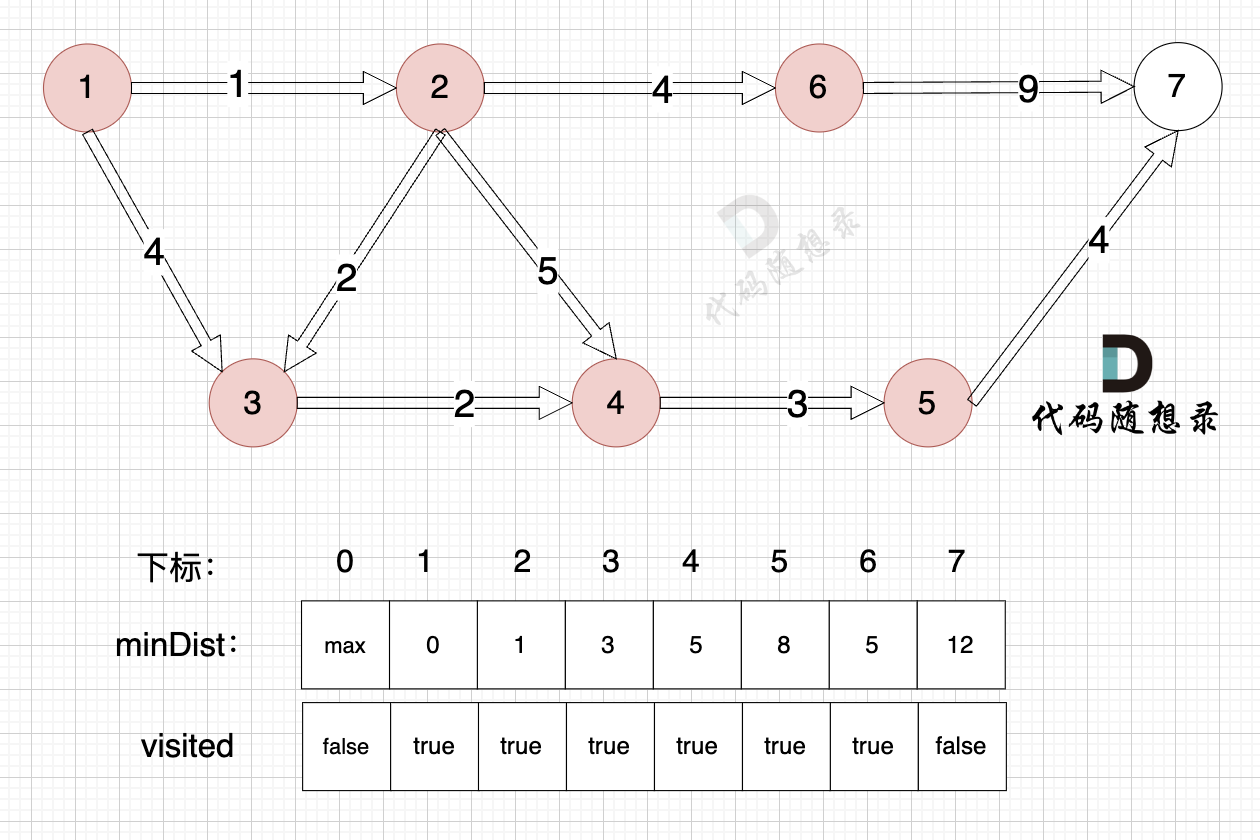
3、更新非访问节点到源点的距离（即更新minDist数组），如图：

由于节点5的加入，那么源点有新的路径可以链接到节点7 所以更新minDist数组：

源点到节点7的最短距离为12，小于原minDist[7]的数值14，更新minDist[7] = 12

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点7（终点），距离源点距离是 12 （minDist[7] = 12）

2、该最近节点被标记访问过

节点7 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组），如图：

节点7加入，但节点7到节点7的距离为0，所以不用更新minDist数组

最后我们要求起点（节点1）到终点（节点7）的距离。

再来回顾一下minDist数组的含义：记录每一个节点距离源点的最小距离。

那么起到（节点1）到终点（节点7）的最短距离就是 minDist[7] ，按上面举例讲解来说，minDist[7] = 12，节点1 到节点7的最短路径为 12。

路径如图：

在上面的讲解中，每一步我都是按照 dijkstra 三部曲来讲解的，理解了这三部曲，代码也就好懂的。

#代码实现

思路

objectivec 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

#define MAXN 1000 // 假设最大节点数为1000

int main() {
    int n, m, p1, p2, val;
    scanf("%d %d", &n, &m);

    // 创建一个邻接矩阵来存储图的边权值
    int grid[MAXN][MAXN];
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            grid[i][j] = INT_MAX; // 初始化为无穷大
        }
    }

    // 输入边的信息
    for (int i = 0; i < m; i++) {
        scanf("%d %d %d", &p1, &p2, &val);
        grid[p1][p2] = val; // 更新边的权值
    }

    int start = 1; // 起始节点
    int end = n;   // 结束节点

    // 存储从源点到每个节点的最短距离
    int minDist[MAXN];
    for (int i = 1; i <= n; ++i) {
        minDist[i] = INT_MAX; // 初始化为无穷大
    }
    minDist[start] = 0; // 起始点到自身的距离为0

    // 记录顶点是否被访问过
    int visited[MAXN] = {0};

    for (int i = 1; i <= n; i++) { // 遍历所有节点
        int minVal = INT_MAX;
        int cur = -1; // 当前节点

        // 1、选距离源点最近且未访问过的节点
        for (int v = 1; v <= n; ++v) {
            if (!visited[v] && minDist[v] < minVal) {
                minVal = minDist[v];
                cur = v;
            }
        }

        if (cur == -1) {
            break; // 如果没有找到未访问节点，结束循环
        }

        visited[cur] = 1; // 2、标记该节点已被访问

        // 3、更新非访问节点到源点的距离
        for (int v = 1; v <= n; v++) {
            if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
                minDist[v] = minDist[cur] + grid[cur][v];
            }
        }
    }

    // 输出结果
    if (minDist[end] == INT_MAX) {
        printf("-1\n"); // 不能到达终点
    } else {
        printf("%d\n", minDist[end]); // 到达终点最短路径
    }

    return 0;
}

学习反思

代码是一个C语言版本的最短路径算法。最短路径算法用于求解图中两个节点之间最短路径的问题。

首先，程序读入了节点数n和边数m。然后，创建一个邻接矩阵grid来存储图的边权值。初始化所有边的权值为无穷大。

接下来，程序通过循环读入边的信息，并更新邻接矩阵中相应边的权值。

然后，程序定义起始节点start和结束节点end，并创建一个数组minDist来存储从起始节点到每个节点的最短距离。将所有节点的最短距离初始化为无穷大，将起始节点的最短距离初始化为0。

程序还创建了一个visited数组来记录节点是否被访问过。初始时，所有节点都未被访问。

接下来，程序使用循环遍历所有节点。在每次循环中，程序选取距离起始节点最近且未被访问过的节点作为当前节点cur。然后，程序标记该节点为已访问，并更新所有未访问节点到起始节点的最短距离。

最后，程序输出结果。如果结束节点的最短距离为无穷大，则表示不能到达终点；否则，输出最短路径的长度。