【贪心算法-第三弹——Leetcode-179.最大数】

1.题目解析

题目来源

测试用例

2.算法原理

3.实战代码

代码解析

*4.贪心策略的合理性证明(离散数学------全序关系)

完全性

反对称性

传递性

---

1.题目解析

题目来源

|-----------------------------------------------------------------------------------|
| 179.最大数------力扣 |

测试用例

2.算法原理

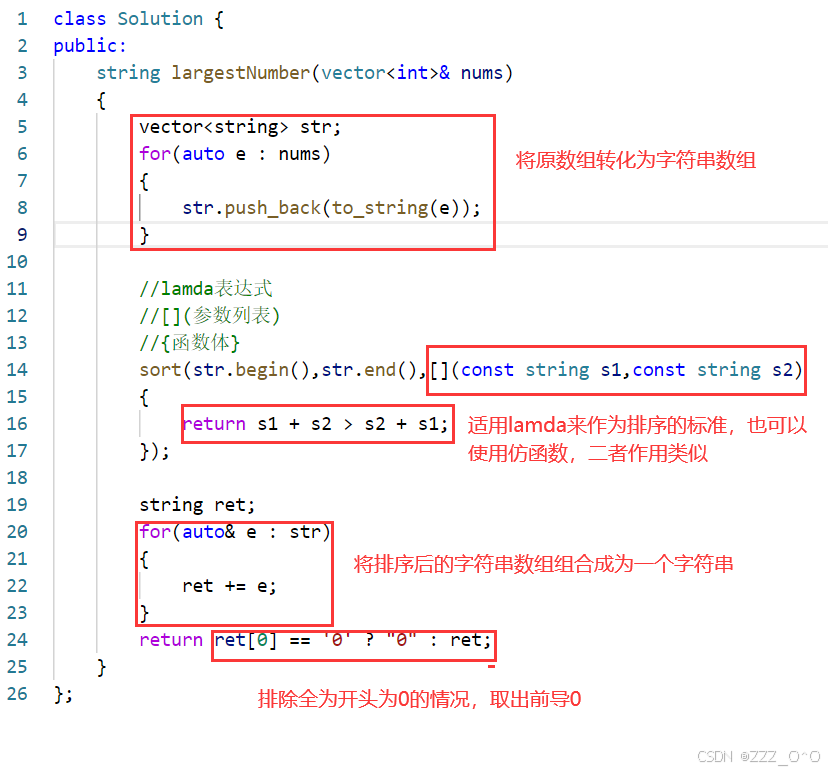
I.由题目我们知道需要返回将数组的所以数字组合形成的一个最大的数字，所以我们可以将整数类型转化为字符串，这样便于运算

II.这里如果使用暴力解法就是从前到后将每个数字高位值更大的排到前面然后不断遍历组合字符串即可，但是这样时间复杂度会很大，不妨使用贪心的思路，这里"贪心"的思路是：

III.需要注意的是当数组中全部是0的情况，此时我们理想的返回值就是一个字符"0"，但是如果不特殊处理上述逻辑就返回的是类似"00000"这样的情况，显然不行。所以我们在最后要判断字符串的首位元素是否为"0"，是的话就直接返回一个字符"0"即可

小tips:为什么上面只需要判断第一个位置是否为字符"0"？因为由排序的底层逻辑可以知道当第一位都是字符"0"时就代表此时整个字符串必定全部为"0"，所以只需要判断第一个即可

3.实战代码

class Solution {
public:
    string largestNumber(vector<int>& nums) 
    {
        vector<string> str;
        for(auto e : nums)
        {
            str.push_back(to_string(e));
        }    

        //lamda表达式 
        //[](参数列表)
        //{函数体}
        sort(str.begin(),str.end(),[](const string s1,const string s2)
        {
            return s1 + s2 > s2 + s1;
        });

        string ret;
        for(auto& e : str)
        {
            ret += e;
        }
        return ret[0] == '0' ? "0" : ret;
    }
};

代码解析

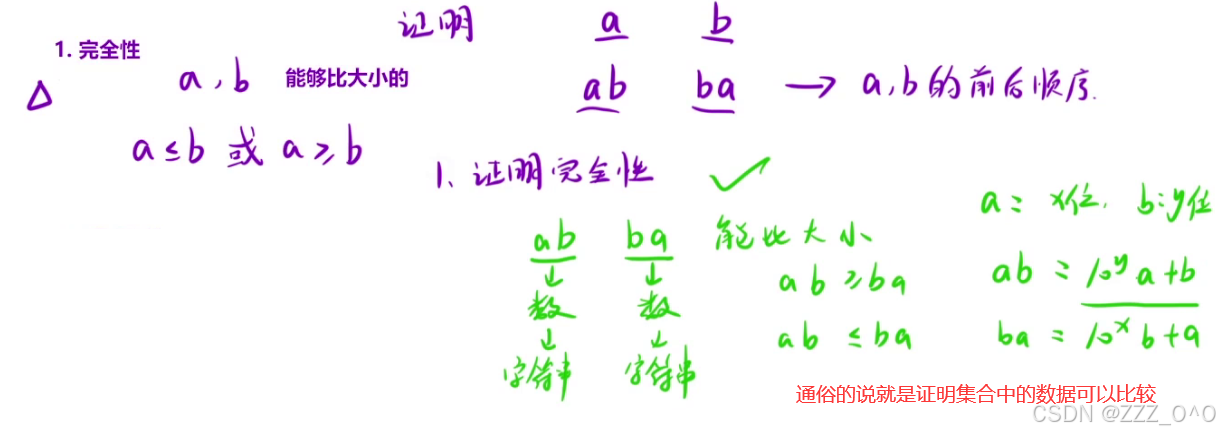
*4.贪心策略的合理性证明(离散数学------全序关系)

完全性

反对称性

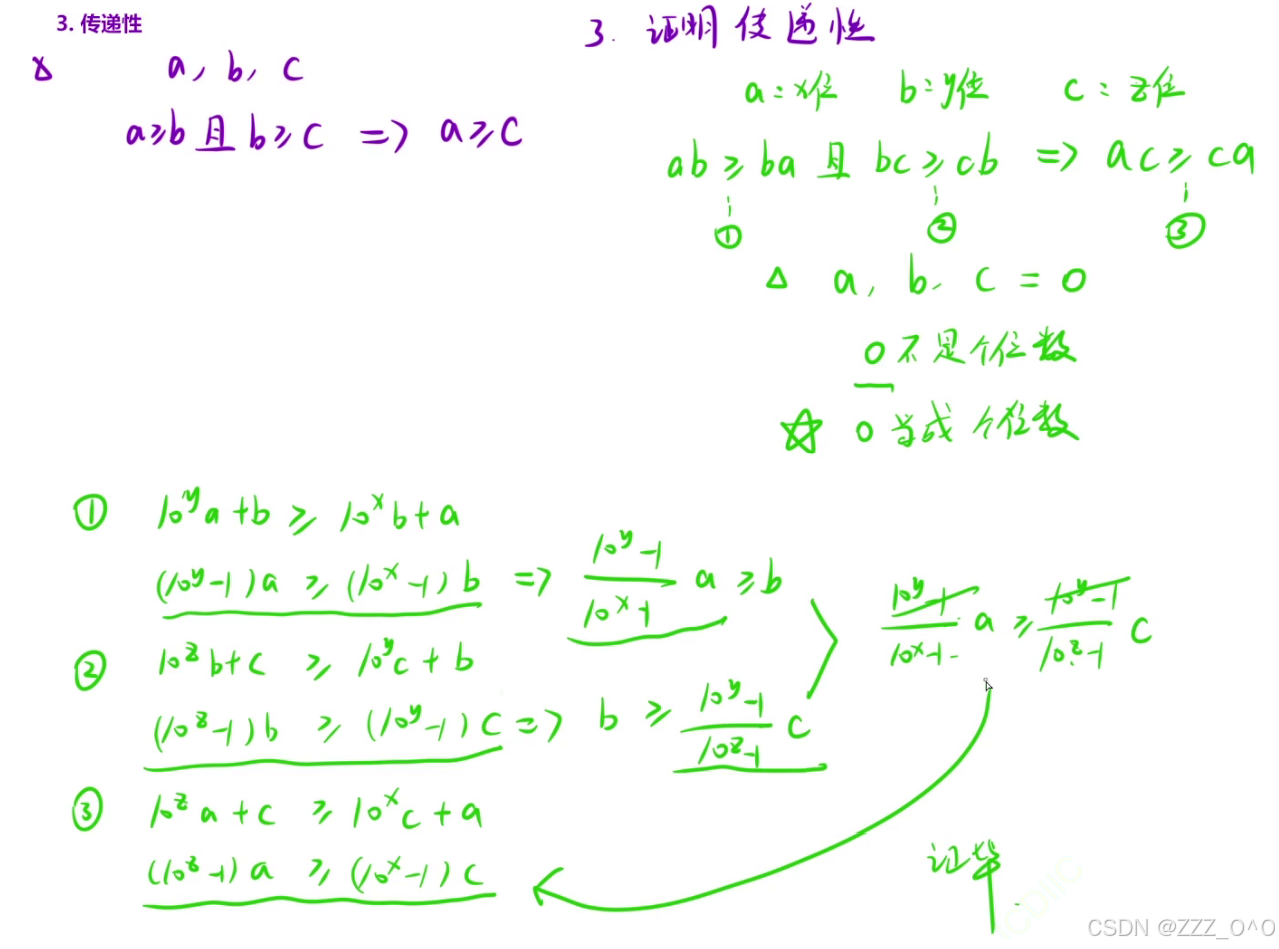
传递性