【Leetcode·中等】如何初始化（583.两个字符串的删除操作·Delete Operation for Two Strings）

其实做动态规划相关题目的朋友难免会碰到该如何初始化 dp 数组的问题，有的解答是 dp $i$ 代表的是 (i-1)，有时候又代表的是 i，那到底是应该用哪种呢？这两种又有什么区别？今天这道题带你整明白嘿嘿😎

题目描述

英文版描述

Given two strings word1 and word2, return the minimum number of steps required to make word1and word2the same.

In one step, you can delete exactly one character in either string.

Example 1:

Input: word1 = "sea", word2 = "eat" Output: 2 Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".

Example 2:

Input: word1 = "leetcode", word2 = "etco" Output: 4

Constraints:

1 <= word1.length, word2.length <= 500
word1 and word2 consist of only lowercase English letters.

英文版地址

https://leetcode.com/problems/delete-operation-for-two-strings/description/https://leetcode.com/problems/delete-operation-for-two-strings/description/

中文版描述

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2相同所需的最小步数。

每步可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat" 输出: 2 解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例 2:

输入： word1 = "leetcode", word2 = "etco" **输出：**4

提示：

1 <= word1.length, word2.length <= 500
word1 和 word2 只包含小写英文字母

中文版地址

https://leetcode.cn/problems/delete-operation-for-two-strings/description/https://leetcode.cn/problems/delete-operation-for-two-strings/description/

解题方法

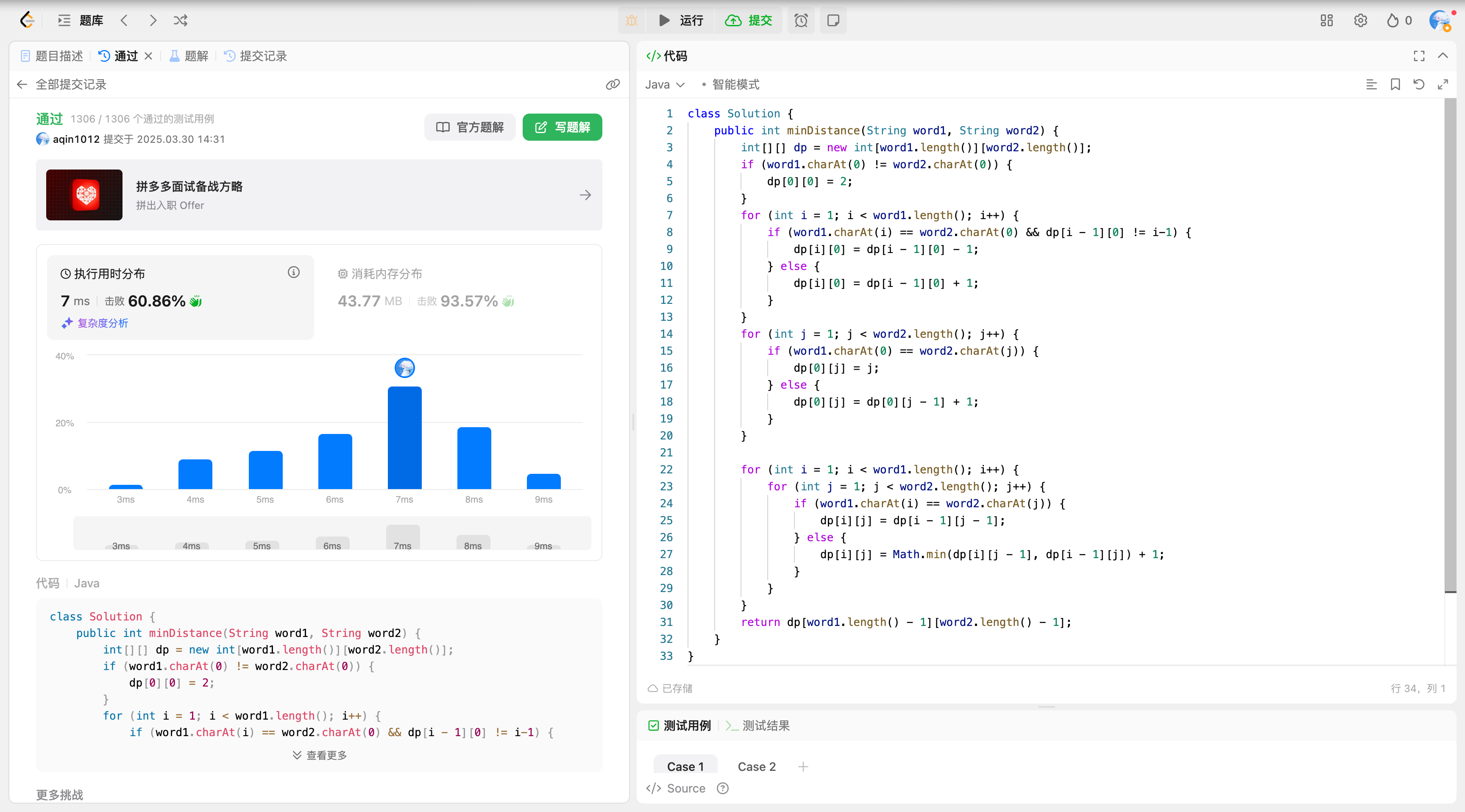
java 复制代码

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length()][word2.length()];
        if (word1.charAt(0) != word2.charAt(0)) {
            dp[0][0] = 2;
        }
        for (int i = 1; i < word1.length(); i++) {
            if (word1.charAt(i) == word2.charAt(0) && dp[i - 1][0] != i-1) {
                dp[i][0] = dp[i - 1][0] - 1;
            } else {
                dp[i][0] = dp[i - 1][0] + 1;
            }
        }
        for (int j = 1; j < word2.length(); j++) {
            if (word1.charAt(0) == word2.charAt(j)) {
                dp[0][j] = j;
            } else {
                dp[0][j] = dp[0][j - 1] + 1;
            }
        }

        for (int i = 1; i < word1.length(); i++) {
            for (int j = 1; j < word2.length(); j++) {
                if (word1.charAt(i) == word2.charAt(j)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j]) + 1;
                }
            }
        }
        return dp[word1.length() - 1][word2.length() - 1];
    }
}

复杂度分析

时间复杂度：O(n*m)，其中 n 是word1的长度，m 是word2的长度
空间复杂度：O(n*m)

官方版

这个初始化就有些不太一样叻～～

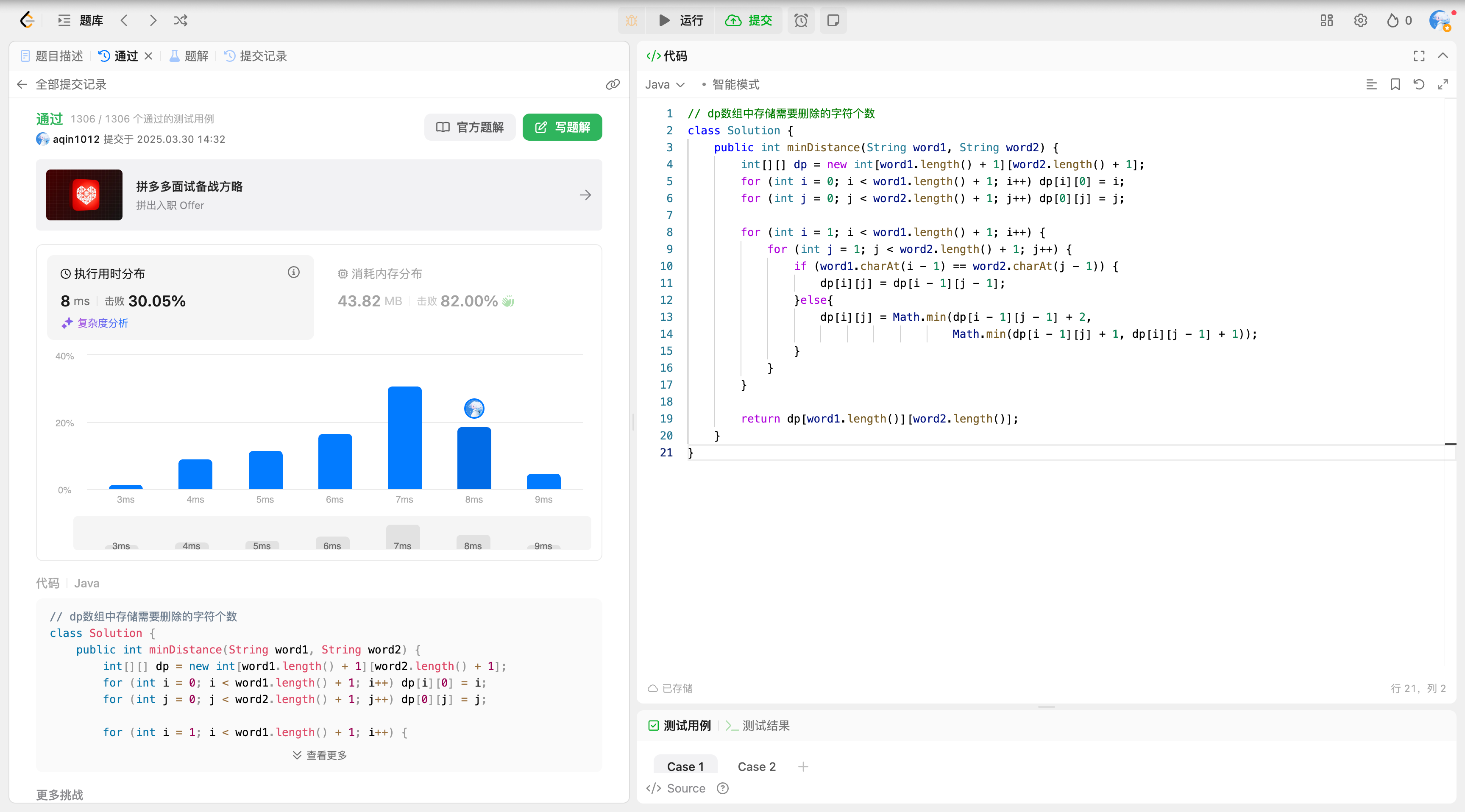
java 复制代码

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;
        for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;
        
        for (int i = 1; i < word1.length() + 1; i++) {
            for (int j = 1; j < word2.length() + 1; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,
                                        Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }
        
        return dp[word1.length()][word2.length()];
    }
}

复杂度分析

时间复杂度：O(n*m)，其中 n 是word1的长度，m 是word2的长度
空间复杂度：O(n*m)

总结

这两种写法的主要差别其实就是在初始化的时候，可以看下他俩的 dp 数组

解法 1 的动规数组的含义是word1 取 $0, i$ 范围内并且word2取 $0, j$ 的范围内时，使得 word1 和 word2 相同所需的最小步数是dp $i$ $j$ ，而解法 2 的动规数组的含义是word1 取 $0, i-1$ 范围内并且word2取 $0, j-1$ 的范围内时，使得 word1 和 word2 相同所需的最小步数是dp $i$ $j$

可以看下下图（示例 2:输入：word1 = "leetcode", word2 = "etco" 输出：4，第一行是解法 1 的 dp 数组，第二行是解法 2 的 dp 数组），或者自己推一遍就会清楚很多

在代码中的体现就是

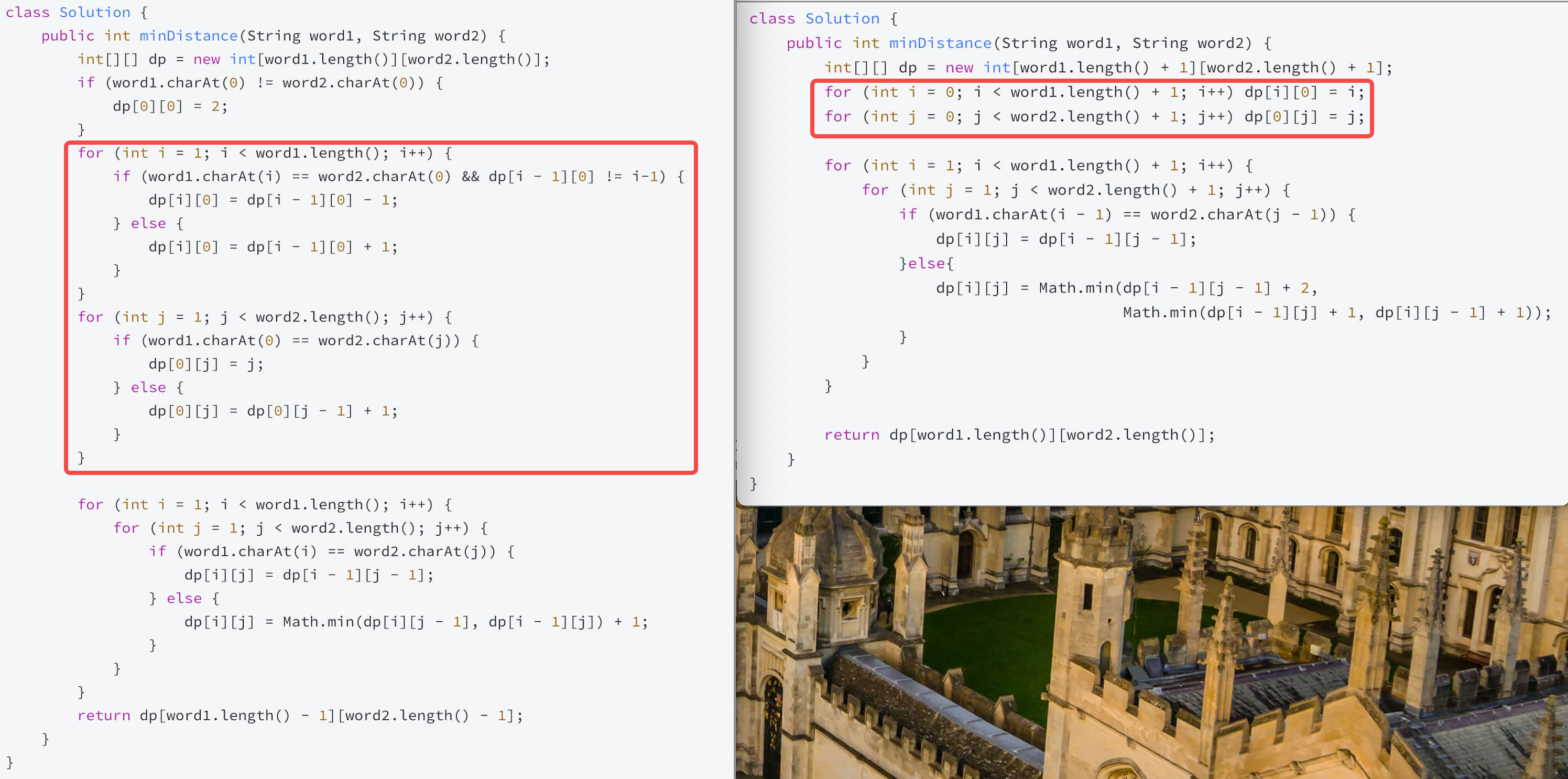
所以如何定义其实并没有对错的问题，只是在处理逻辑上会有一些些差异～～