0201线性回归-机器学习-人工智能

文章目录

- - [1 程序目标](#1 程序目标)
  - [2 代码实现](#2 代码实现)
  - [3 关键步骤解释](#3 关键步骤解释)
  - [4 示例输出](#4 示例输出)
  - [5 注意事项](#5 注意事项)
  - 结语

以下是一个使用 scikit-learn、pandas和 matplotlib 实现线性回归的完整程序示例。程序包含数据加载、模型训练、预测和可视化。

1 程序目标

加载数据 （使用 pandas）
数据预处理（划分训练集和测试集）
训练线性回归模型 （scikit-learn）
模型评估（计算误差指标）
可视化结果 （matplotlib）

2 代码实现

python

复制

python 复制代码

# 导入必要的库
import matplotlib
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


matplotlib.use('TkAgg')

# 设置 Matplotlib 使用支持中文的字体
plt.rcParams['font.sans-serif'] = ['Noto Sans CJK SC']  # 根据字体名称调整
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# ======================
# 1. 加载数据
# ======================
# 示例数据集（可以替换为你的 CSV 文件路径）
# 假设数据文件包含特征列 'AT', 'V', 'AP', 'RH' 和目标列 'PE'
data = pd.read_csv('./ccpp.csv')  # 替换为你的文件路径

# 或者使用 scikit-learn 内置数据集（例如波士顿房价）
# from sklearn.datasets import load_boston
# boston = load_boston()
# data = pd.DataFrame(boston.data, columns=boston.feature_names)
# data['PRICE'] = boston.target

# ======================
# 2. 数据预处理
# ======================
# 提取特征 X 和目标 y
X = data[['AT', 'V', 'AP', 'RH']]  # 特征列
y = data['PE']                     # 目标列

# 划分训练集和测试集（80% 训练，20% 测试）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# ======================
# 3. 训练线性回归模型
# ======================
model = LinearRegression()       # 创建模型
model.fit(X_train, y_train)      # 训练模型

# ======================
# 4. 预测与评估
# ======================
y_pred = model.predict(X_test)   # 预测测试集

# 计算误差指标
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"模型系数: {model.coef_}")    # 特征权重
print(f"截距项: {model.intercept_}") # 截距
print(f"均方误差 (MSE): {mse:.2f}")  # 误差越小越好
print(f"R² 分数: {r2:.2f}")         # 越接近1越好

# ======================
# 5. 可视化结果
# ======================
# 绘制真实值与预测值对比图
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.5)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--')  # 理想对角线
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.title("真实值 vs 预测值")
plt.show()

# 绘制残差图（误差分布）
residuals = y_test - y_pred
plt.figure(figsize=(10, 6))
plt.scatter(y_pred, residuals, alpha=0.5)
plt.hlines(0, y_pred.min(), y_pred.max(), colors='r', linestyles='dashed')
plt.xlabel("预测值")
plt.ylabel("残差")
plt.title("残差分析")
plt.show()

3 关键步骤解释

数据加载 ：
- 使用 pandas 读取 CSV 文件，或直接加载内置数据集。
- 确保特征列 (X) 和目标列 (y) 正确分离。
数据划分 ：
- train_test_split 将数据随机分为训练集和测试集，random_state 确保可重复性。
模型训练 ：
- LinearRegression() 创建模型，.fit() 方法用训练数据拟合模型。
模型评估 ：
- 均方误差 (MSE)：预测值与真实值的平均平方误差，越小越好。
- R² 分数：模型解释数据变异的比例，1 表示完美拟合。
可视化 ：
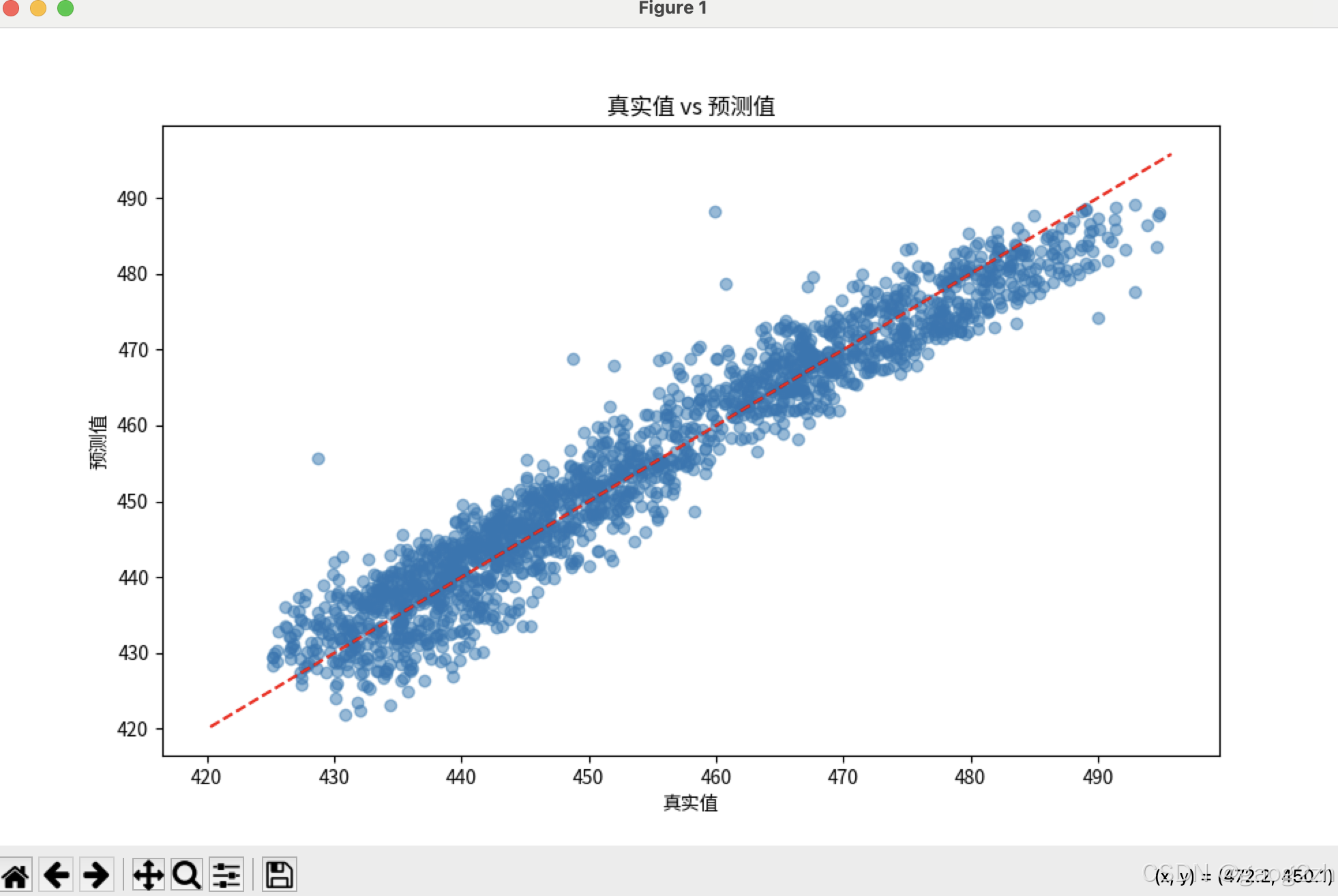
- 真实值 vs 预测值：理想情况下点应沿红色对角线分布。
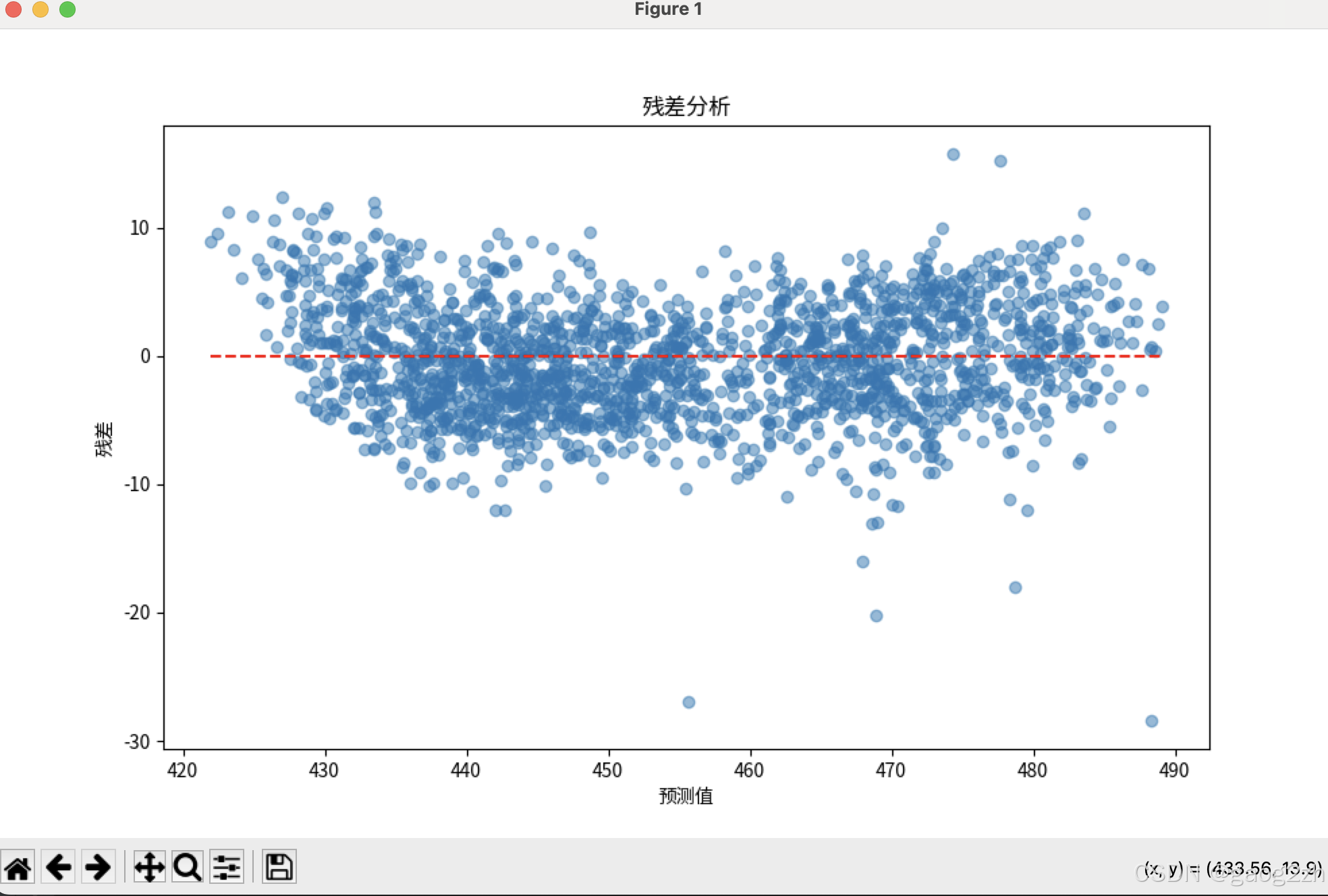
- 残差图：残差应随机分布在 0 附近，无明显模式。

4 示例输出

复制

复制代码

模型系数: [-1.97 -0.23  0.06 -0.15]
截距项: 454.42
均方误差 (MSE): 18.32
R² 分数: 0.93

5 注意事项

数据预处理 ：
- 如果数据存在缺失值，需使用 data.dropna() 或填充方法（如均值填充）。
- 如果特征量纲差异大，建议标准化（StandardScaler）。
模型改进 ：
- 若线性回归效果不佳，可尝试多项式回归或正则化（Ridge/Lasso）。
- 检查特征之间的多重共线性（使用 data.corr()）。
替换数据 ：
- 将代码中的 ccpp.csv 替换为你的实际数据路径，并调整特征列名。
- 示例中数据参考下面链接1

效果如下图所示：

结语

❓QQ:806797785

⭐️仓库地址：https://gitee.com/gaogzhen

⭐️仓库地址：https://github.com/gaogzhen

1\][](https://www.cnblogs.com/pinard/p/6016029.html)[用scikit-learn和pandas学习线性回归](https://www.cnblogs.com/pinard/p/6016029.html)\[CP/OL\].