【算法】单词搜索、最短距离

单词搜索

这道题主要考察了深度优先遍历(DFS)算法。

我们通过几个简单例子来分析一些细节问题：

要搜索的单词串：abc

搜索的过程中必须按照字母顺序，首先从矩阵中的第一个元素开始搜索，遇到字母a则开始深度优先遍历，搜索周围满足条件的字母，这种情况是可以找到的。

2.待搜索单词串：aba

此时是无法找到的，但是这里想一想从头开始遍历矩阵遇到字母a，则开始深度优先遍历，在到字母b，此时对于字母b它的周围也是有已经遍历过的字母a的，如果不对字母a进行标记就会对字母a再进行遍历，那答案就错了，因此我们要对矩阵中满足条件并且已经被遍历过的字母进行标记。

3.待搜索单词串：srds

首先会从矩阵中第一个字母进行深度优先遍历，因此矩阵中的第一个字母s会被标记，由于字母s周围的字母没有与待搜索单词匹配的因此会接着遍历矩阵，直到遇到下一个字母s，此时就会通过深度优先遍历到矩阵中的第一个字母s处，如果此时这个字母s是被标记的状态那就会搜索失败，因此要在最开始当矩阵中第一个字母s退出深度优先遍历时，必须要将其标记取消，这是一个细节。

cpp 复制代码

class Solution {
public:
    int arr_x[4] = {-1,1,0,0};
    int arr_y[4] = {0,0,-1,1};
    bool arr_judge[6][6] = {false};
    bool exist(vector<vector<char>>& board, string word) {
        for(int i = 0;i < board.size();++i){
            for(int j = 0;j < board[0].size();++j){
                if(board[i][j] == word[0]){
                    if(dfs(board,word,i,j,0)){
                    return true;
                }
                }
            }
        }
        return false;
    }
    bool dfs(const vector<vector<char>>& board,const string& word,int i,int j,int pos)
    {
        if(pos == word.length()-1){
            return true;
        }
        arr_judge[i][j] = true;
        for(int k = 0;k < 4;++k){
            int x = i + arr_x[k];
            int y = j + arr_y[k]; //注意
            if(x >= 0 && x < board.size() && y >= 0 && y < board[0].size() && !arr_judge[x][y] && board[x][y] == word[pos+1]){
                if(dfs(board,word,x,y,pos+1)){
                    return true;
                }
            }
        }
        arr_judge[i][j] = false; //将该位置取消标记
        return false;
    }
};

最短距离

运动员男女组成一个矩形方阵，计算每个人离最近的女生的距离（相邻两个人之间的距离为1）

题目描述输入：一个矩阵，0代表女，1代表男，

输出：一个同样大小的矩阵，每个元素是其距离最近的女生的距离

下面是一个简单的示例：

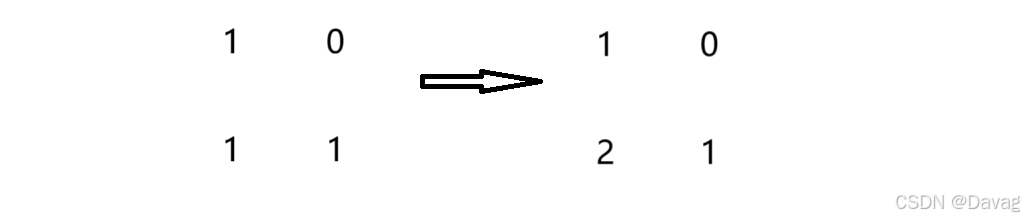
这道题可以使用广度优先遍历(BFS)来做：

cpp 复制代码

vector<vector<int>> shortestDistance(const vector<vector<int>>& vv)
{
	int rows = vv.size();
	int cols = vv[0].size();
	vector<vector<int>> res(rows, vector<int>(cols, INT_MAX));
	queue<pair<int, int>> q;
	//先将矩阵中的女生对应的最短距离设为0
	for (int i = 0;i < rows;++i)
	{
		for (int j = 0;j < cols;++j)
		{
			if (0 == vv[i][j])
			{
				res[i][j] = 0;
				q.push({ i,j });
			}
		}
	}
	int x[4] = { -1,1,0,0 };
	int y[4] = { 0,0,-1,1 };
	while (!q.empty())
	{
		pair<int, int> p = q.front();
		int X = p.first;
		int Y = p.second;
		q.pop();
		for (int i = 0;i < 4;++i)
		{
			int newX = X + x[i];
			int newY = Y + y[i];
			if (newX >= 0 && newX < cols && newY >= 0 && newX < rows && res[X][Y] + 1 < res[newX][newY])
										//res[X][Y] + 1 < res[newX][newY]这个条件很关键
			{
				res[newX][newY] = res[X][Y] + 1;
				q.push(pair<int, int>(newX, newY));
			}
		}
	}
	return res;
	//pair<int, int> p(1, 2);
	//auto& [a, b] = p; //C++17新特性结构化绑定
}