文章目录
一、实验目的
深入理解Huffman树和Huffman编码的原理,熟练掌握其构造算法。通过设计Huffman树的数据存储结构,实现对给定字符频率构造Huffman树及生成Huffman编码的过程,提升对数据压缩等实际问题的解决能力,培养算法设计、调试和分析的综合素养。
二、实验描述
已知某系统在通信联络中只可能出现6种字符,其使用频率如下表所示:
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.07 | 0.09 | 0.12 | 0.22 | 0.23 | 0.27 |
根据Huffman编码原理,为这6种字符设计一种Huffman编码方案。具体步骤包括:依据给定字符的权值,按照Huffman算法构造Huffman树,再基于该树生成每个字符对应的Huffman编码。
三、基本要求
- 设计Huffman树的数据存储结构:采用结构体数组来存储Huffman树的节点信息。每个结构体包含节点的值、权重、父结点索引、左孩子索引和右孩子索引等成员。例如:
c
typedef struct {
float weight;
int parent, lchild, rchild;
} HTNode, *HuffmanTree;这样的结构可以方便地记录Huffman树节点之间的关系和相关属性,为后续的树构造和编码生成提供基础。
- 理解并掌握构造Huffman树、求Huffman编码原理及算法 :
-
构造Huffman树 :严格按照Huffman算法步骤,从给定的字符权值出发,不断选取权值最小的两棵子树合并成新树,直至集合中只剩一棵树。在此过程中,深入理解每次合并操作对树结构和权值分布的影响。
-
求Huffman编码 :在得到Huffman树后,从每个叶子节点出发,向根节点回溯,根据经过的分支方向(左分支记为'0',右分支记为'1')生成对应的编码。理解这种编码方式如何保证编码的前缀特性,即任意一个字符的编码都不是另一个字符编码的前缀,从而实现高效的数据压缩和解码。
-
完善参考程序,在程序中的下划线处填入适当语句 :仔细研读参考程序,明确每个下划线处的功能需求。依据Huffman树的构造和编码生成算法逻辑,准确填入相应语句,确保程序能够正确实现从字符权值到Huffman树构建,再到编码生成的完整过程。可能涉及节点的初始化、权值比较、树的合并、编码回溯等操作的代码补充。
-
设计测试数据,上机调试、测试完善后的参考程序,保存并打印测试结果,对算法性能进行分析 :
-
设计测试数据 :除了给定的6种字符及其频率数据外,额外设计多组不同规模和权值分布的测试数据,包括字符种类较少、较多,权值分布均匀、不均匀等情况,以全面测试程序的正确性和鲁棒性。
-
上机调试、测试 :在集成开发环境中输入完善后的程序,运用断点调试、输出中间变量值等手段,排查程序中的语法错误和逻辑错误。针对不同测试数据运行程序,观察输出结果是否符合预期。
-
保存并打印测试结果 :将每次测试的输入数据、程序输出的Huffman编码结果等信息保存下来,并打印输出,以便后续分析。
-
算法性能分析 :从时间复杂度和空间复杂度两方面分析算法性能。时间复杂度主要取决于Huffman树的构造过程,涉及多次权值比较和树的合并操作,为 O ( n log n ) O(n \log n) O(nlogn),其中 n n n 为字符种类数;空间复杂度取决于存储Huffman树节点的结构体数组大小,为 O ( 2 n − 1 ) O(2n - 1) O(2n−1) 。结合测试结果,分析算法在不同规模数据下的运行效率和存储开销,探讨优化方向。
四、算法分析
- Huffman算法 :
- 时间复杂度 :在构造Huffman树时,每次都需要从集合中选取权值最小的两棵树,若使用优先队列(如堆)来管理树的集合,每次选取和合并操作的时间复杂度为 O ( log n ) O(\log n) O(logn) ,总共需要进行 n − 1 n - 1 n−1 次合并操作,所以构造Huffman树的时间复杂度为 O ( n log n ) O(n \log n) O(nlogn) 。
- 空间复杂度 :需要使用结构体数组存储Huffman树的节点,节点数为 2 n − 1 2n - 1 2n−1 ,所以空间复杂度为 O ( 2 n − 1 ) O(2n - 1) O(2n−1) 。
- 求Huffman编码算法 :
- 时间复杂度 :对于每个叶子节点,都需要从叶子向根回溯生成编码,回溯路径长度最大为树的高度,即 O ( log n ) O(\log n) O(logn) ,共有 n n n 个叶子节点,所以求Huffman编码的时间复杂度为 O ( n log n ) O(n \log n) O(nlogn) 。
- 空间复杂度 :除了存储Huffman树的空间外,还需要额外空间存储每个字符的编码,编码长度与树的高度相关,总体空间复杂度仍为 O ( 2 n − 1 ) O(2n - 1) O(2n−1) (考虑到编码存储开销相对树节点存储可忽略不计,主要空间占用仍在树节点存储)。
五,示例代码
cpp
#include <stdio.h>
#define MAX 21
typedef struct { // 定义Huffman树结点结构
char data; // 结点值
int weight; // 权重
int parent; // 父结点
int lchild; // 左孩子
int rchild; // 右孩子
} HTNode;
typedef struct { // 定义Huffman编码结构
char cd[MAX];
int start;
} HCode;
void CreatHT(HTNode *HT, int n) {
int i, k, lnode, rnode;
int m1, m2;
for (i = 1; i < 2 * n; i++)
HT[i].parent = HT[i].lchild = HT[i].rchild = 0; // 初始化
for (i = n + 1; i < 2 * n; i++) { // 构造Huffman树
m1 = m2 = 0x7fff; // m1取最小权重,m2取次小权重
lnode = rnode = 0; // lnode, rnode分别取两个最小权重的结点位置
for (k = 1; k < i; k++) {
if (HT[k].parent == 0) {
if (HT[k].weight < m1) {
m2 = m1;
rnode = lnode;
m1 = HT[k].weight;
lnode = k;
} else if (HT[k].weight < m2) {
m2 = HT[k].weight;
rnode = k;
}
}
}
HT[lnode].parent = i;
HT[rnode].parent = i;
HT[i].weight = m1 + m2;
HT[i].lchild = lnode;
HT[i].rchild = rnode;
}
}
void CreatHCode(HTNode *HT, HCode *hcd, int n) {
int i, f, c;
HCode hc;
for (i = 1; i <= n; i++) {
hc.start = n;
c = i;
f = HT[i].parent;
while (f != 0) {
if (HT[f].lchild == c) // c是f的左孩子,编码取'0',否则取'1'
hc.cd[--hc.start] = '0';
else
hc.cd[--hc.start] = '1';
c = f; // 向根结点方向搜索
f = HT[f].parent;
}
hcd[i] = hc;
}
}
void PrintHCode(HTNode *HT, HCode *hcd, int n) {
int i, k;
for (i = 1; i <= n; i++) {
printf(" %c:", HT[i].data);
for (k = hcd[i].start; k < n; k++)
printf("%c", hcd[i].cd[k]);
printf("\n");
}
}
int main() {
int i, n;
HTNode HT[2 * MAX - 1];
HCode hcd[MAX];
printf("(1)创建Huffman树......\n");
do {
printf(" 请输入元素个数(1-%d):", MAX - 1);
scanf("%d", &n);
} while (n < 1 || n > MAX - 1); // 确保n值合规
for (i = 1; i <= n; i++) { // Huffman树结点存放在ht数组从1下标开始的位置
fflush(stdin);
printf(" 第%d个元素的结点值==>", i);
scanf("%c", &HT[i].data);
printf("\t权重==>");
scanf("%d", &HT[i].weight);
}
CreatHT(HT, n);
printf(" Huffman树创建成功!\n");
fflush(stdin);
getchar();
printf("(2)创建Huffman编码......\n");
CreatHCode(HT, hcd, n);
printf(" Huffman编码创建成功!\n");
getchar();
printf("(3)输出Huffman编码:\n");
PrintHCode(HT, hcd, n);
return 0;
} 六,实验操作
1,双击Visual Studio程序快捷图标,启动程序。

2,之前创建过项目的话,直接打开即可,这里选择【创建新项目】。

3,单击选择【空项目】------单击【下一步】按钮。
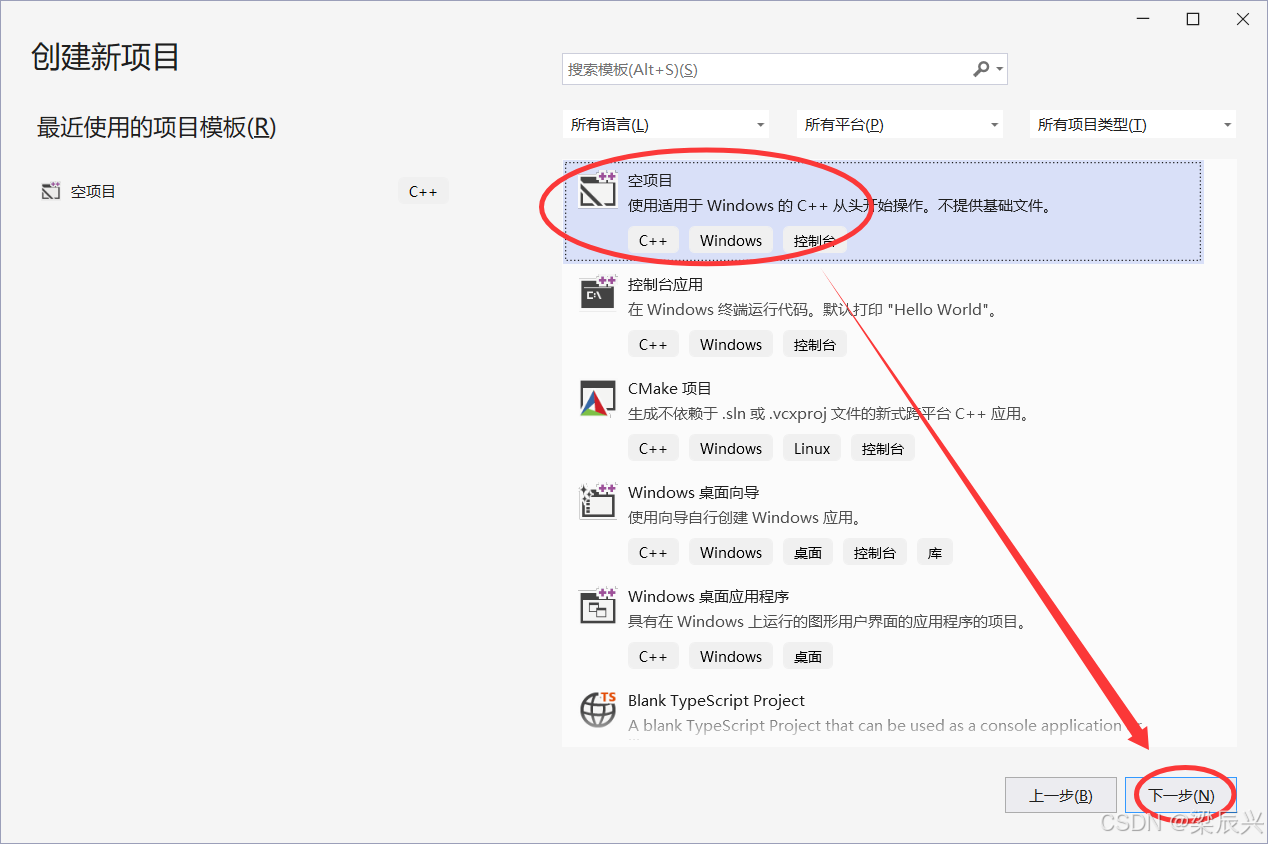
4,编辑好项目的名称和存放路径,然后单击【创建】按钮。

5,创建C++程序文件,右击【源文件】------选择【添加】------【新建项】。

6,输入项目名称,单击【添加】按钮。

7,编写代码,单击运行按钮,运行程序。
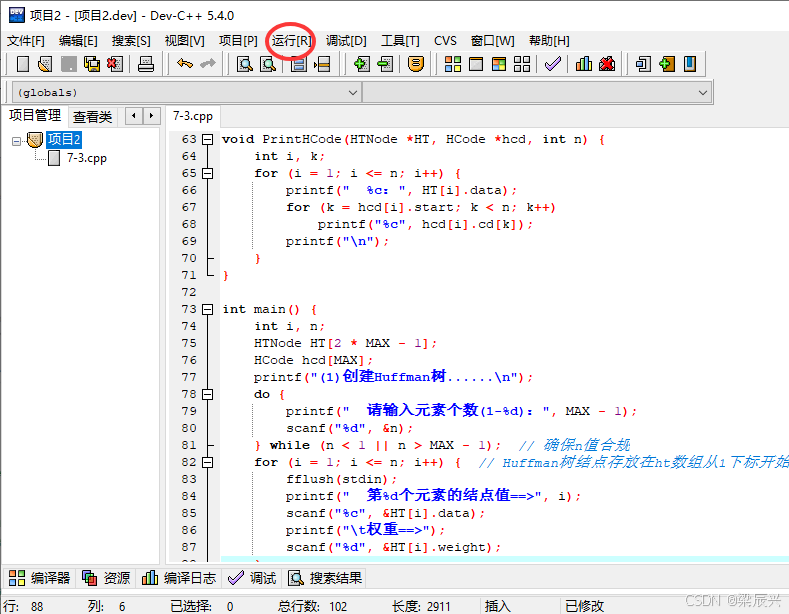
七,运行结果
1,实验要求的结果。

2,编写代码运行后的结果。
