摘要
本文对多层感知机(MLP)、卷积神经网络(CNN)、循环神经网络(RNN)和注意力机制等深度学习核心架构的内部运作机制进行可视化分析。通过展示参数学习过程、激活映射和注意力分布等关键特征,揭示了"黑箱"模型的内部工作原理,为模型可解释性研究提供直观理解。实验结果表明,可视化技术不仅能够揭示神经网络的特征提取和表示学习过程,还能帮助研究者理解模型的决策逻辑,为网络架构优化和模型设计提供有力支持。
1. 引言
深度学习在计算机视觉、自然语言处理和强化学习等多个领域取得了突破性进展[1,2]。然而,深度神经网络通常被视为"黑箱"系统,其内部表示和决策逻辑难以被人类直观理解。这种不透明性限制了模型的可信度和应用范围,尤其在医疗诊断、自动驾驶等高风险场景中[3]。
可视化作为解决这一问题的重要途径,能够将抽象的数学模型转换为可视的图像表示,帮助研究者和实践者探索网络的内部状态和行为[4]。本研究利用可视化技术,对不同类型的神经网络架构进行剖析,包括:
-
多层感知机(MLP)的参数学习和决策边界演化
-
卷积神经网络(CNN)的特征激活映射
-
循环神经网络(RNN)的时序动态建模
-
注意力机制的权重分布和多头注意力模式
2. 多层感知机:参数空间与决策边界演化
2.1 理论基础
多层感知机作为深度学习的基础架构,由多层全连接神经元组成,形式上可表示为一系列非线性变换[5]:
h\^{(l)} = \\sigma(W\^{(l)}h\^{(l-1)} + b\^{(l)})
其中h\^{(l)}表示第l层的隐藏表示,W\^{(l)}和b\^{(l)}分别为权重矩阵和偏置向量,\\sigma为非线性激活函数(如ReLU、Sigmoid等)。
2.2 可视化分析
我们通过二维螺旋分类问题,演示MLP学习过程中的参数空间和决策边界变化。图1展示了训练初期的网络状态:

初始阶段,网络权重接近随机初始化状态,决策边界呈现简单的线性分割,无法有效区分非线性可分的螺旋数据。这符合Goodfellow等人[6]关于神经网络优化早期阶段的研究发现。
图2展示了训练结束时的网络状态:
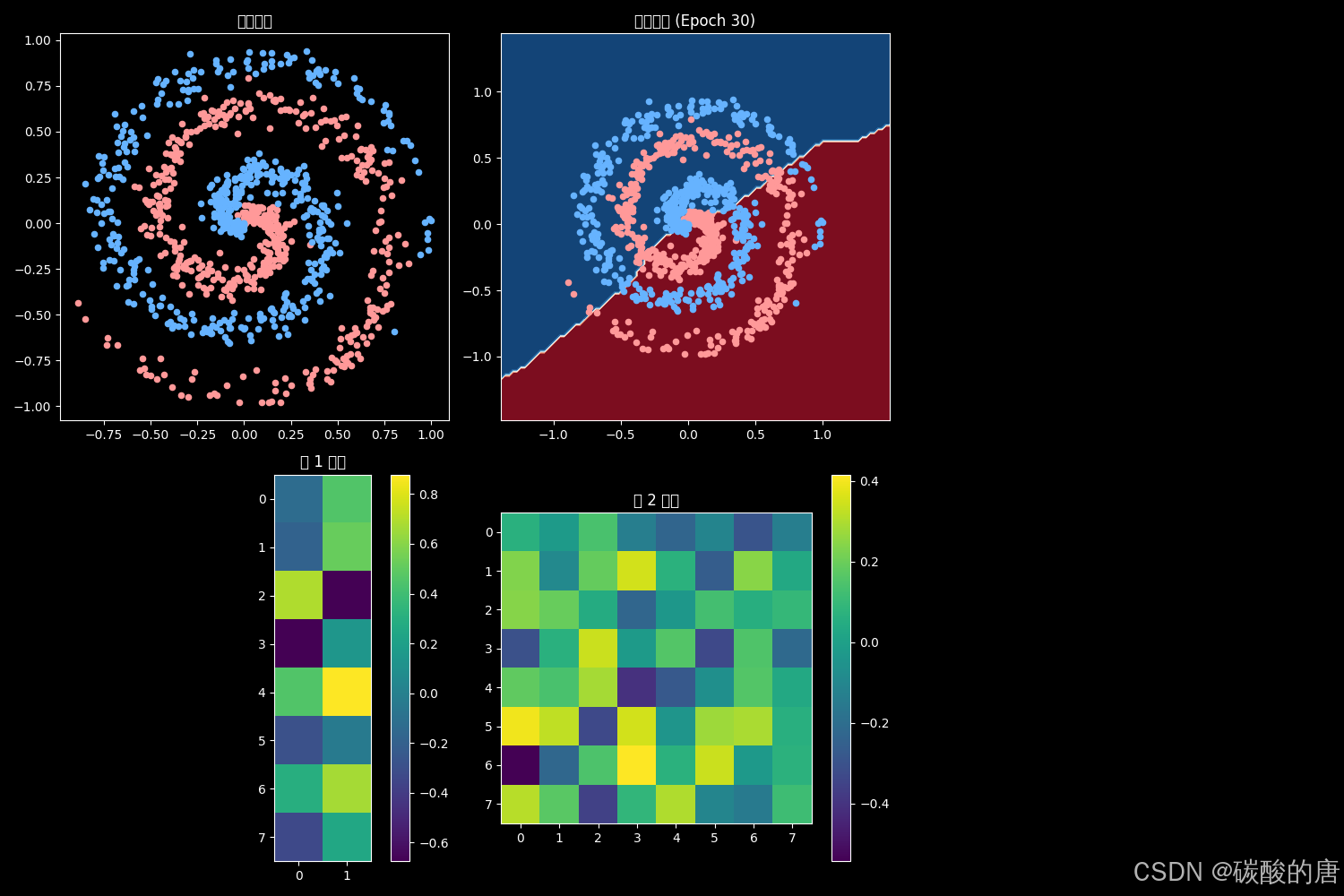
经过30轮训练,网络权重发生了显著变化,形成了复杂的非线性决策边界,成功捕捉了数据的螺旋形态。权重矩阵可视化揭示了各层神经元学习到的特征检测器,这与Zeiler和Fergus[7]关于神经网络表示学习的研究结果一致。
完整的训练过程可通过视频直观观察:
mlp_training
视频展示了MLP从线性到非线性决策边界的渐进式学习过程,验证了梯度下降优化中的"先拟合简单模式,后学习复杂特征"理论[8]。
3. 卷积神经网络:层级特征提取可视化
3.1 理论基础
卷积神经网络通过局部感受野、权重共享和空间池化等机制,特别适合处理具有网格拓扑结构的数据[9]。卷积层的数学表达式为:
h_{i,j}\^{(l)} = \\sigma(\\sum_{m=0}\^{F_h-1}\\sum_{n=0}\^{F_w-1} W_{m,n}\^{(l)} \\cdot h_{i+m,j+n}\^{(l-1)} + b\^{(l)})
其中F_h \\times F_w为卷积核尺寸,W\^{(l)}为卷积核权重。
3.2 可视化分析
我们通过激活映射技术[10],展示了CNN各层的特征提取过程:

图3展示了CNN处理输入图像时各层的激活状态。值得注意的是,网络呈现出明显的层级特征提取模式:
-
浅层卷积(Conv1)捕获边缘、纹理等低级特征
-
中间层(Conv2)组合低级特征形成部件和模式
-
深层表示则包含更抽象的语义信息
这一发现支持了Yosinski等人[11]提出的深度CNN层级表示学习理论,即网络从低级到高级逐层构建特征表示。特别是ReLU激活后的特征图显示出显著的稀疏激活模式,这与Glorot等人[12]关于ReLU促进表示稀疏性的研究结果一致。
4. 循环神经网络:时序动态与长程依赖
4.1 理论基础
循环神经网络专为处理序列数据设计,通过隐藏状态传递实现时序建模[13]。LSTM作为RNN的一种重要变体,引入了门控机制解决梯度消失问题[14]:
f_t = \\sigma(W_f \\cdot \[h_{t-1}, x_t\] + b_f)
i_t = \\sigma(W_i \\cdot \[h_{t-1}, x_t\] + b_i)
o_t = \\sigma(W_o \\cdot \[h_{t-1}, x_t\] + b_o)
\\tilde{c}_t = \\tanh(W_c \\cdot \[h_{t-1}, x_t\] + b_c)
c_t = f_t \\odot c_{t-1} + i_t \\odot \\tilde{c}_t
h_t = o_t \\odot \\tanh(c_t)
其中f_t、i_t、o_t分别为遗忘门、输入门和输出门,c_t为细胞状态,h_t为隐藏状态,\\odot表示Hadamard积。
4.2 可视化分析
我们通过隐藏状态热力图和预测性能可视化,探索LSTM的时序动态特性:

图4展示了LSTM处理时间序列数据时隐藏状态单元的动态变化。热力图清晰显示了某些神经元在特定时间模式上的选择性激活,这与Karpathy等人[15]关于LSTM神经元功能特化的研究发现相符。
为验证模型的序列学习能力,我们进行了正弦波预测实验:

图5展示了LSTM在时间序列预测任务上的表现。模型成功捕捉了数据的周期性变化模式,验证了Graves[16]关于LSTM时序模式建模能力的研究结果。值得注意的是,模型在预测长程依赖时表现出色,这支持了Hochreiter和Schmidhuber[14]最初提出的LSTM长程记忆假设。
5. 注意力机制:选择性信息处理
5.1 理论基础
注意力机制通过动态加权输入信息,实现选择性信息处理[17]。自注意力机制的计算过程可形式化为:
\\text{Attention}(Q, K, V) = \\text{softmax}\\left(\\frac{QK\^T}{\\sqrt{d_k}}\\right)V
其中Q、K、V分别为查询、键和值矩阵,d_k为键向量的维度。多头注意力则并行计算多组注意力:
\\text{MultiHead}(Q, K, V) = \\text{Concat}(\\text{head}_1, \\ldots, \\text{head}_h)W\^O
\\text{where}\~\\text{head}_i = \\text{Attention}(QW\^Q_i, KW\^K_i, VW\^V_i)
5.2 可视化分析
我们通过注意力权重热力图,探索多头注意力机制的工作原理:

图6展示了四个不同注意力头的权重分布。显著观察包括:
-
各注意力头表现出不同的关注模式,支持了Vaswani等人[18]关于多头机制捕获不同类型依赖关系的假设
-
对角线区域高激活表明模型重视当前位置信息
-
非对角线区域激活揭示了序列中远距离依赖的建模
这些观察与Clark等人[19]关于Transformer模型中注意力头功能分化的研究结果一致,证实了多头注意力在捕获复杂结构依赖方面的优势。
6. 讨论与结论
本研究通过可视化技术,揭示了不同类型神经网络的内部工作机制。主要发现包括:
-
MLP通过参数学习,逐步构建从简单到复杂的决策边界
-
CNN呈现明显的层级特征提取模式,从低级局部特征到高级语义表示
-
RNN/LSTM展现出选择性时序记忆,能有效建模长程依赖关系
-
注意力机制实现了多粒度信息选择,通过多头并行处理捕获复杂依赖关系
这些发现为深度学习模型的可解释性研究提供了有价值的见解,并为神经网络架构设计和优化提供了直观指导。实验结果支持了Zeiler和Fergus[7]、Yosinski等人[11]提出的网络可视化有助于理解模型行为的观点。
随着深度学习向更复杂、更大规模模型发展,可视化分析将在模型透明度和可解释性研究中发挥越来越重要的作用。未来工作将探索更高维特征空间的可视化技术,以及动态交互式可视化系统的构建,进一步推动神经网络"黑箱"的开放与理解。
参考文献
1\] LeCun, Y., Bengio, Y., \& Hinton, G. (2015). Deep learning. \*Nature\*, 521(7553), 436-444. \[2\] Krizhevsky, A., Sutskever, I., \& Hinton, G. E. (2012). ImageNet classification with deep convolutional neural networks. \*NeurIPS\*. \[3\] Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. \*Nature Machine Intelligence\*, 1(5), 206-215. \[4\] Visualization techniques for neural networks, Samek, W., Montavon, G., Vedaldi, A., Hansen, L. K., \& Müller, K. R. (2019). \*Explainable AI: Interpreting, Explaining and Visualizing Deep Learning\*. \[5\] Goodfellow, I., Bengio, Y., \& Courville, A. (2016). \*Deep Learning\*. MIT Press. \[6\] Goodfellow, I. J., Vinyals, O., \& Saxe, A. M. (2015). Qualitatively characterizing neural network optimization problems. \*ICLR\*. \[7\] Zeiler, M. D., \& Fergus, R. (2014). Visualizing and understanding convolutional networks. \*ECCV\*. \[8\] Arpit, D., Jastrzębski, S., Ballas, N., Krueger, D., Bengio, E., Kanwal, M. S., ... \& Lacoste-Julien, S. (2017). A closer look at memorization in deep networks. \*ICML\*. \[9\] LeCun, Y., Bottou, L., Bengio, Y., \& Haffner, P. (1998). Gradient-based learning applied to document recognition. \*Proceedings of the IEEE\*, 86(11), 2278-2324. \[10\] Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., \& Batra, D. (2017). Grad-CAM: Visual explanations from deep networks via gradient-based localization. \*ICCV\*. \[11\] Yosinski, J., Clune, J., Nguyen, A., Fuchs, T., \& Lipson, H. (2015). Understanding neural networks through deep visualization. \*ICML Deep Learning Workshop\*. \[12\] Glorot, X., Bordes, A., \& Bengio, Y. (2011). Deep sparse rectifier neural networks. \*AISTATS\*. \[13\] Elman, J. L. (1990). Finding structure in time. \*Cognitive Science\*, 14(2), 179-211. \[14\] Hochreiter, S., \& Schmidhuber, J. (1997). Long short-term memory. \*Neural Computation\*, 9(8), 1735-1780. \[15\] Karpathy, A., Johnson, J., \& Fei-Fei, L. (2016). Visualizing and understanding recurrent networks. \*ICLR Workshop\*. \[16\] Graves, A. (2013). Generating sequences with recurrent neural networks. \*arXiv preprint arXiv:1308.0850\*. \[17\] Bahdanau, D., Cho, K., \& Bengio, Y. (2015). Neural machine translation by jointly learning to align and translate. \*ICLR\*. \[18\] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... \& Polosukhin, I. (2017). Attention is all you need. \*NeurIPS\*. \[19\] Clark, K., Khandelwal, U., Levy, O., \& Manning, C. D. (2019). What does BERT look at? An analysis of BERT's attention. \*ACL BlackboxNLP Workshop\*.