

前引: 本篇作为初阶结尾的最后一篇---排序,将先介绍八种常用的排序方法,然后开始刷题,小编会详细注释每句代码的作用,不会出现看不懂的情况,这点大家放心,既是写给大家同时也是写给自己的!已经迫不及待想看看Hoare大佬的排序了!各种分组分组排序的思想如何在题目中得到体现?突破口在哪!~~以下排序实现我们最优先实现单趟,再实现整体!由易到难!
【注:本文仅仅是作为复习使用,完整的思维讲解可打开小编主页,有详细教程讲解哦!】
目录
稳定排序与不稳定排序有哪些
稳定:冒泡排序、直接插入排序、归并排序
不稳定: 快速排序、堆排序、选择排序、希尔排序
直接插入排序
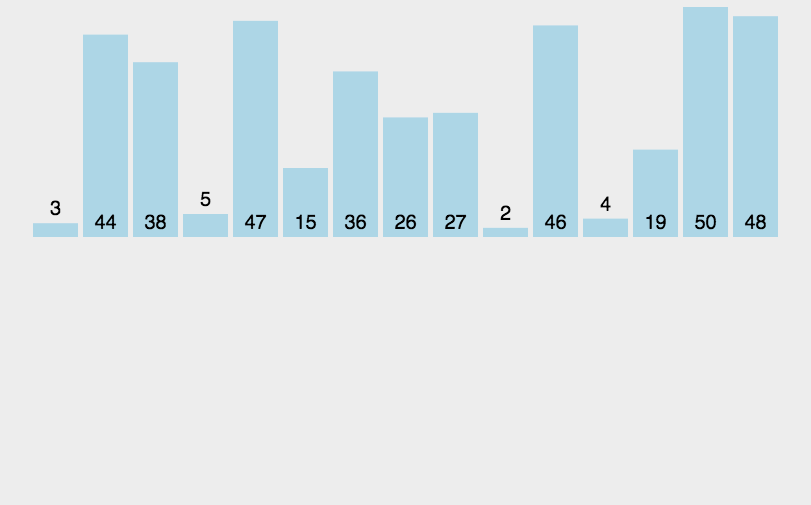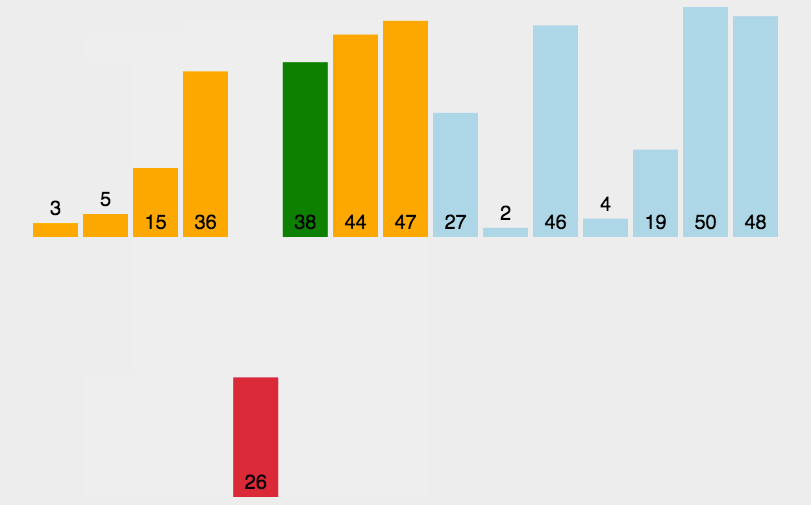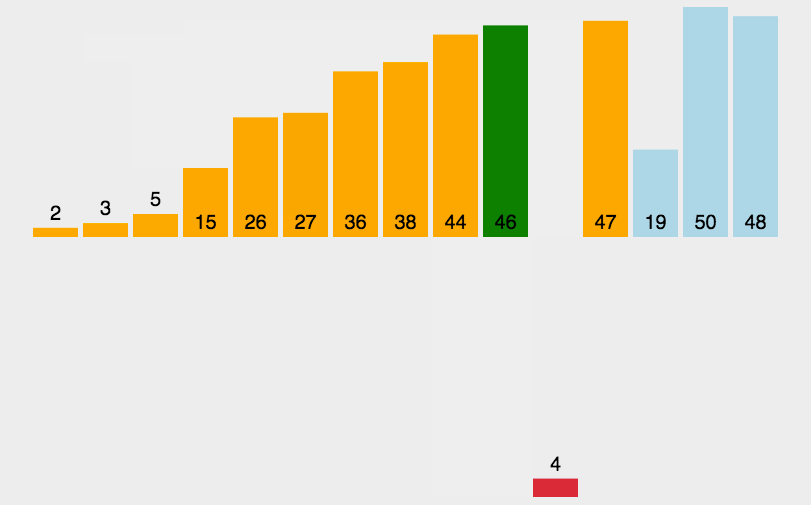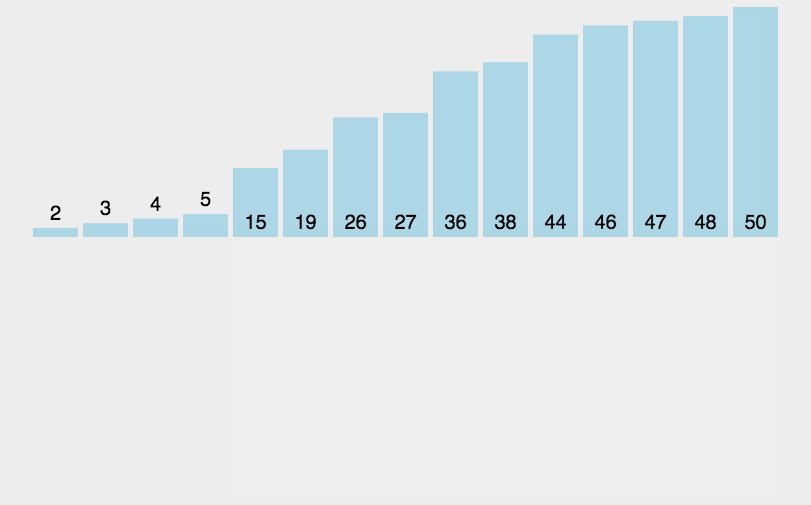
实现思路:
从第一个元素开始,默认第一个元素是有序的,将其之后的元素与前面的进行依次比较, 根据条件进行移动、插入
单趟实现
整体实现

cpp
//直接插入排序
void Direct(int* arr, int size)
{
//断言
assert(arr);
for (int i = 1; i < size; i++)
{
//单趟
//待比元素(待比元素刚开始应该在待排元素的前一位)
int end = i-1;
//待排元素
int tmp = arr[i];
while (end >= 0)
{
//如果待排的比比较的元素小,就后移
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
//比较元素后移
end--;
}
else
break;
//此时说明待排元素大于等于end位置的元素 或者 已经到数组末尾
}
//插入
arr[end + 1] = tmp;
}
}复杂度:
时间复杂度最坏:O(N^2) 空间复杂度:O(1)
希尔排序

实现思路:
希尔排序是在直接插入排序上的优化,从大概有序到整体有序,避免了最坏情况。将一个数组分组,保证每组间隔一致,将每组进行直接插入排序,再整体实现直接插入排序
单趟实现(注意待排元素不越界)

整体实现达到大概有序

再进行一趟直接插入排序达到整体有序

cpp
//希尔排序
void Shell(int* arr, int size)
{
//断言
assert(arr);
//设置间隔
int val = 3;
for (int j = 0; j < val; j++)//外出循环控制end的起始位置
{
//单趟(内层循环控制end、tmp的位置)
for (int i = j; i + val < size; i += val)
{
//待比元素
int end = i;
//待排元素
int tmp = arr[end + val];
while (end >= 0)
{
//如果待排元素小于待比元素就前移
if (arr[end] > tmp)
{
arr[end + val] = arr[end];
//end前移val个单位
end -= val;
}
else
break;
}
//循环结束代表满足插入条件
arr[end + val] = tmp;
}
}
Direct(arr, size);
}代码优化:
假如有一万个数据,那么间隔val就太短了不适合,我们可以让间隔为每次的二分之一,根据长度选择间隔。最后间隔会达到1,同时也就不用去再接入直接插入排序的接口了

复杂度:
优化之前时间复杂度最坏情况:O(N^2)
优化之后明显感觉更效率:外层*内层O(logN)* O(N)
空间复杂度:O(1)
堆排序


实现思路:
利用堆的向上调整、向下调整来存储数据,再利用多次出堆顶元素来完成排序。下面小编用大顶堆、从下标1开始存储来实现堆排序
实现堆:
cpp
//建推
Heap Heapspace;
cpp
//初始化
void Perliminary(Heap* Heapspace)
{
//初始化变量
Heapspace->max = MAX;
Heapspace->size = 0;
Heapspace->data = (int*)malloc(sizeof(int) * Heapspace->max);
if (Heapspace->data == NULL)
{
printf("初始化失败\n");
return;
}
}
//交换函数
void Exchange(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//上浮调整
void Upward(int* data,int child)
{
//设置父节点下标
int parent = child / 2;
while (parent > 0)
{
//如果子节点大于父节点,就交换
if (data[child] > data[parent])
{
Exchange(&data[child], &data[parent]);
//更新父节点、子节点
child = parent;
parent = child / 2;
}
else
break;
}
}
//入堆
void Enter(Heap* Heapspace, int data)
{
//判断堆是否存满,是则扩容
if (Heapspace->size == Heapspace->max)
{
int* pc = (int*)malloc(sizeof(int) * (Heapspace->max) * 2);
if (pc == NULL)
{
printf("空间扩容失败\n");
return;
}
//更新堆信息
Heapspace->max *= 2;
Heapspace->data = pc;
}
//入堆
Heapspace->size++;
Heapspace->data[Heapspace->size] = data;
//上浮调整
Upward(Heapspace->data, Heapspace->size);
}
//打印堆元素
void Printf_Heap(Heap Heapspace, int size)
{
printf("堆元素:");
for (int i = 1; i <= size; i++)
{
printf("%d ", Heapspace.data[i]);
}
printf("\n");
}
//下沉调整
void Subsidence(Heap* Heapspace)
{
//设置子节点、父节点下标
int parent = 1;
int child = 2 * parent;
//堆尾堆顶交换
Exchange(&Heapspace->data[1], &Heapspace->data[Heapspace->size]);
//出堆顶元素
if (Heapspace->size > 1)
{
Heapspace->size--;
}
while (parent > 0 && child <= Heapspace->size)
{
//找左右子节点最大值
if (child <= Heapspace->size && Heapspace->data[child] < Heapspace->data[child + 1])
{
child++;
}
//调整堆顶
if (child <= Heapspace->size && Heapspace->data[parent] < Heapspace->data[child])
{
Exchange(&Heapspace->data[parent], &Heapspace->data[child]);
//调整下标
parent = child;
child = 2 * parent;
}
else
break;
}
}堆排序:
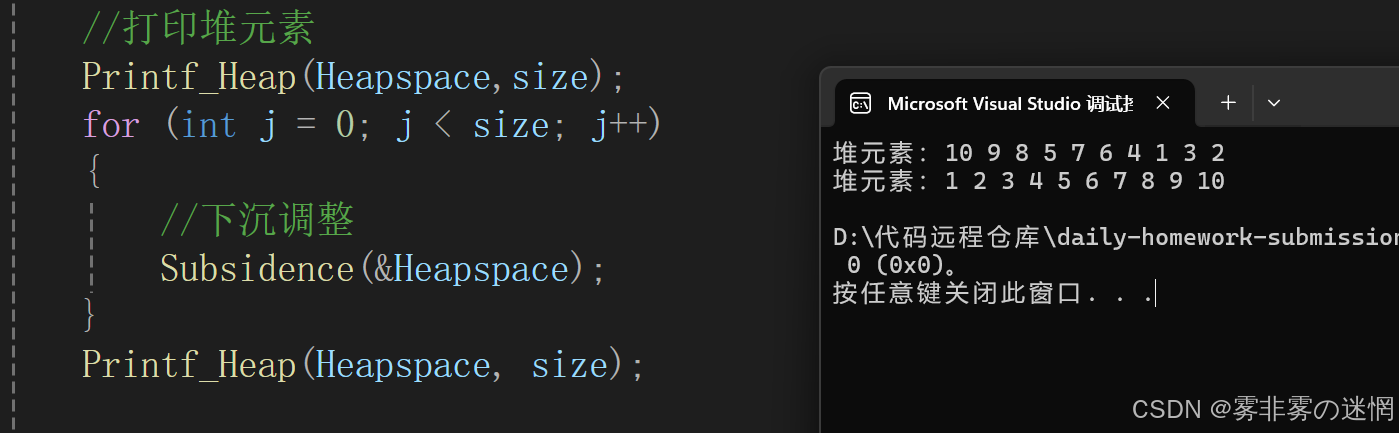
利用堆的下沉调整:每次将堆尾元素与堆顶元素交换,然后调整堆以保持大顶堆的性质,多次调整达到排序效果
cpp
for (int j = 0; j < size; j++)
{
//下沉调整
Subsidence(&Heapspace);
}
复杂度:
时间复杂度为O(N logN),空间复杂度为O(1)
冒泡排序
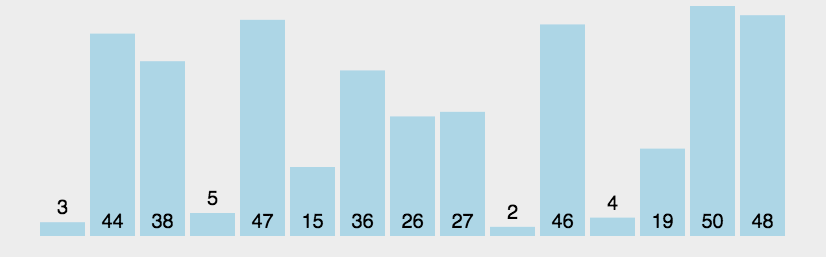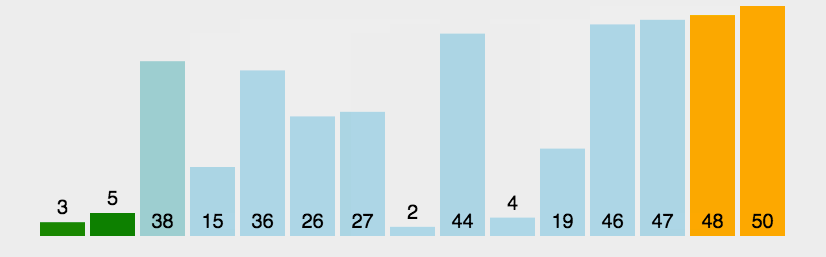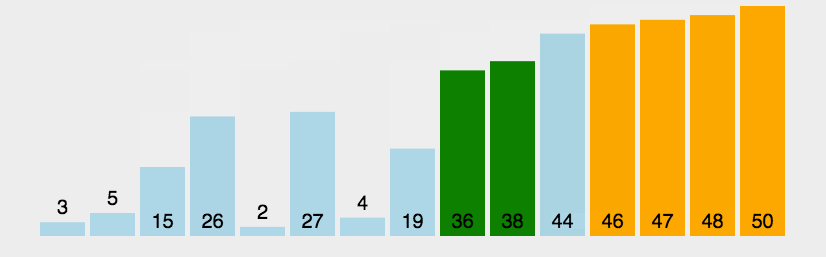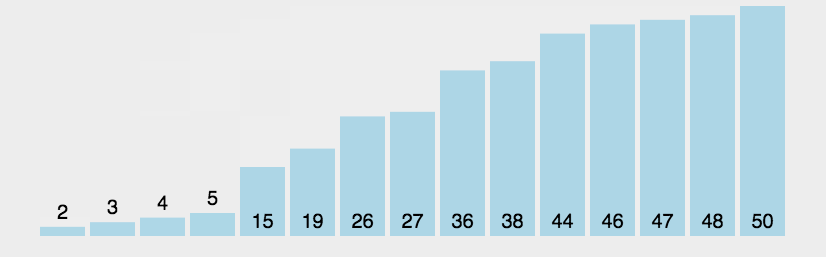
实现思路:
从第一个元素开始,与之后的所有元素进行比较,较大则交换位置,直至排完所有元素
单趟实现: 
整体实现:

cpp
//冒泡排序
void Bubbles(int* arr, int size)
{
//断言
assert(arr);
for (int i = 1; i < size; i++)
{
//单趟
for (int end = 0; end < size - 1; end++)
{
//如果大于后面的元素,就交换
if (arr[end] > arr[end + 1])
{
Exchange(&arr[end], &arr[end + 1]);
}
}
}
}代码优化:
如果经过单趟,没有任何排序过程,说明整体都是有序的,可以直接结束循环

复杂度:
时间复杂度:O(N^2),空间复杂度:O(1)
选择排序
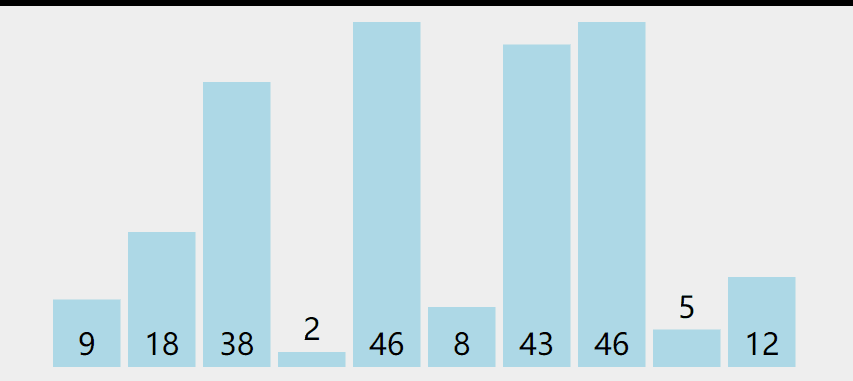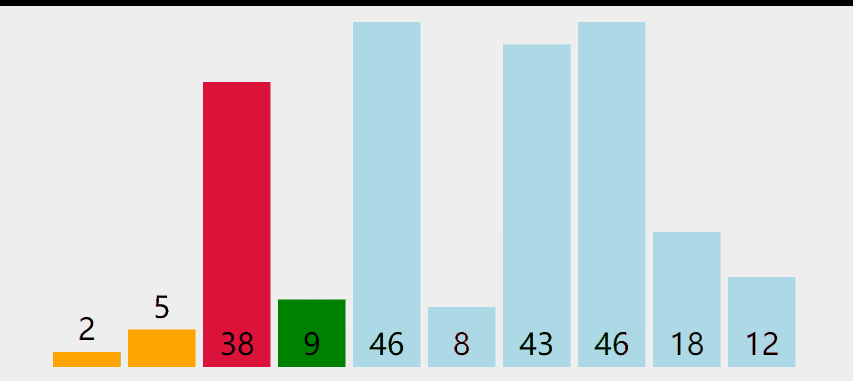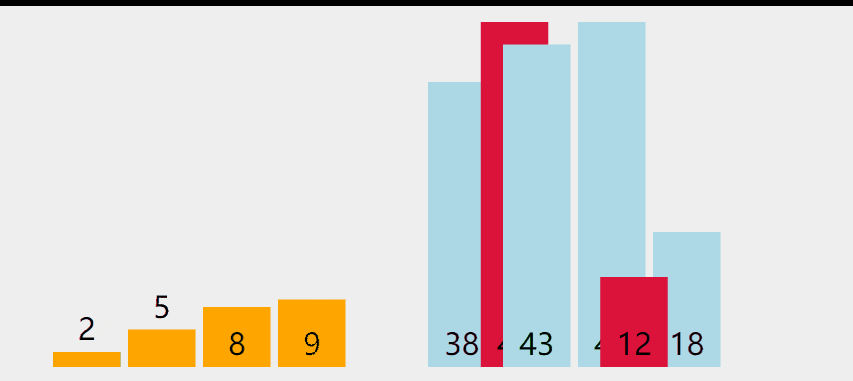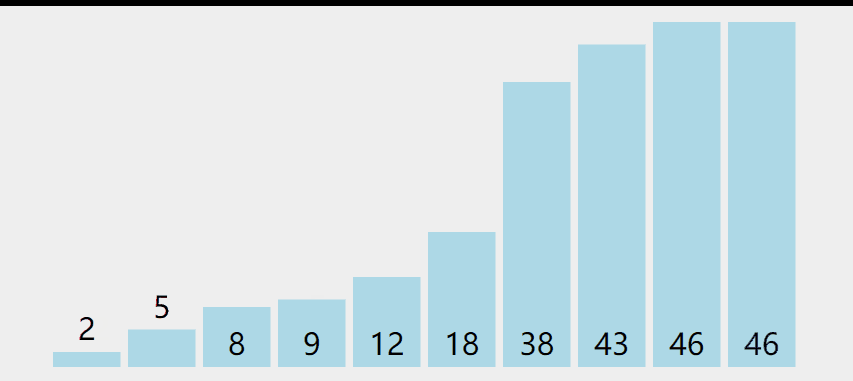
实现思路:
开始整个数组都是无序的额,找整个无序组中的最小值,与有序部分的末尾进行交换,一直重复
单趟实现:
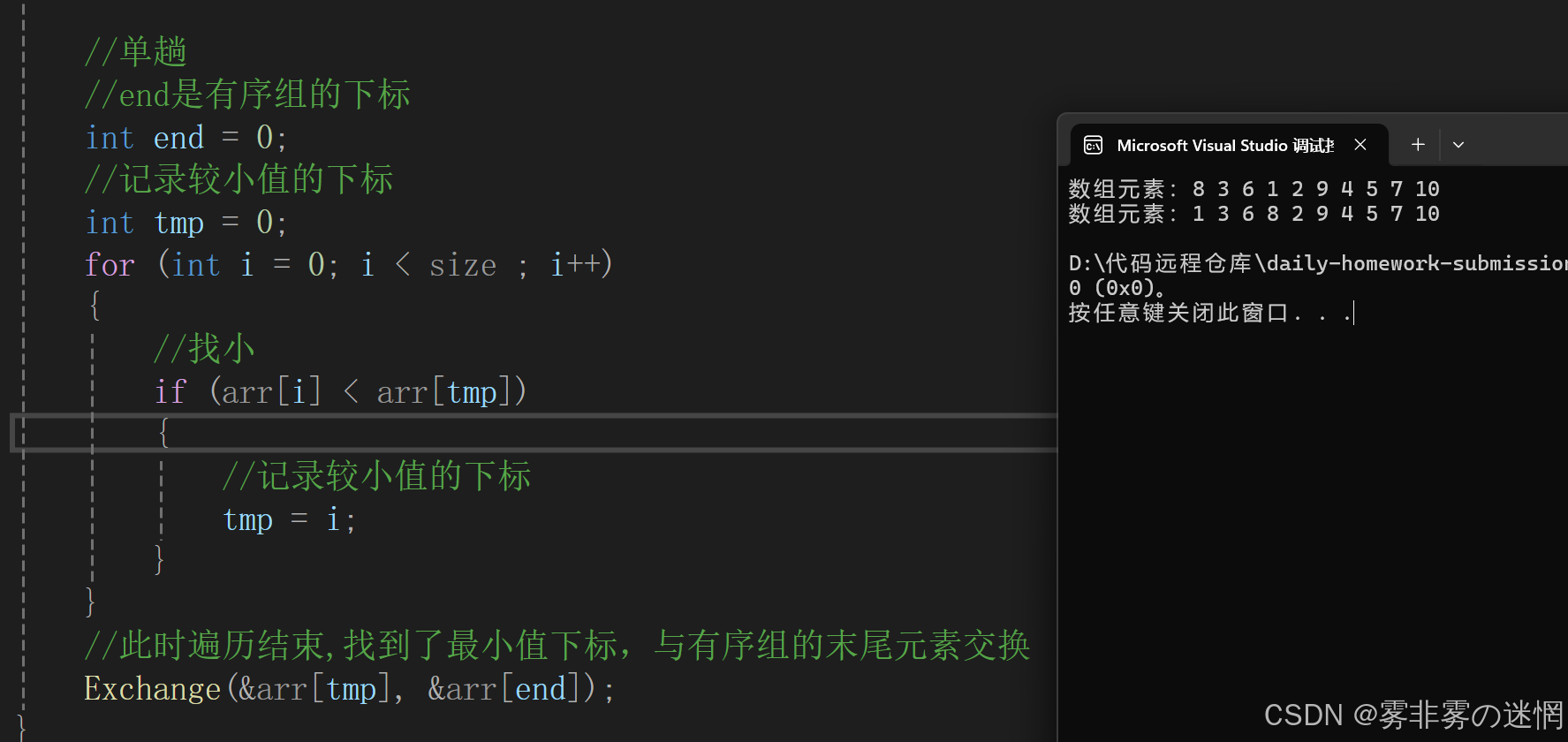
整体实现:

cpp
//选择排序
void Select(int* arr, int size)
{
//断言
assert(arr);
//end是有序组的下标
int end = 0;
//记录较小值的下标
int tmp = 0;
for (int i = 0; i < size - 1; i++)
{
//第二次遍历应该从end的位置开始
tmp = end;
//单趟
for (int i = end; i < size; i++)
{
//找小
if (arr[i] < arr[tmp])
{
//记录较小值的下标
tmp = i;
}
}
//此时遍历结束,找到了最小值下标,与有序组的末尾元素交换
Exchange(&arr[tmp], &arr[end]);
//更新end
end++;
}
}复杂度:
时间复杂度:O(N^2),空间复杂度:O(1)
Hoare排序
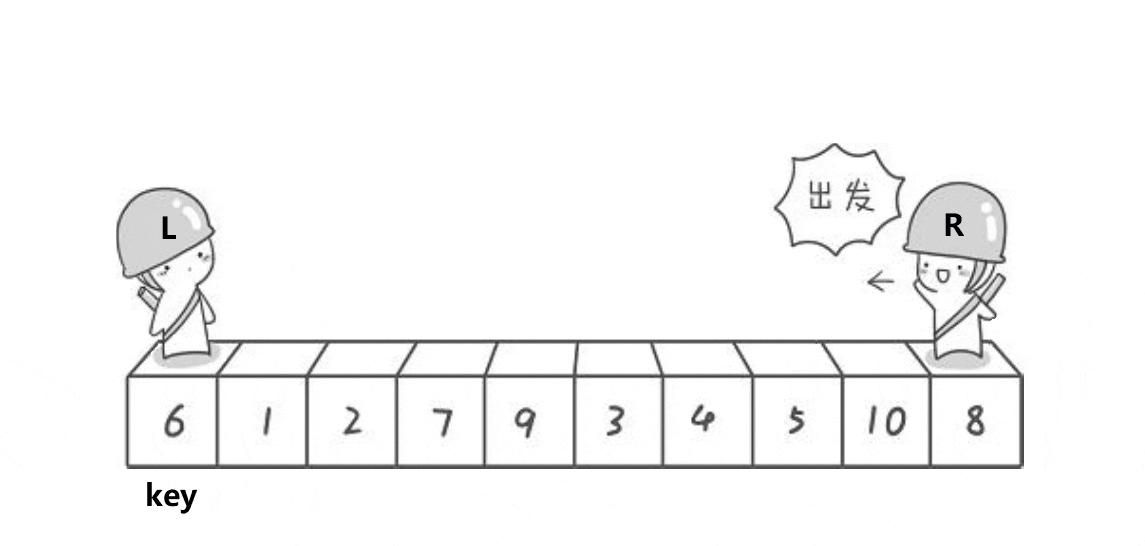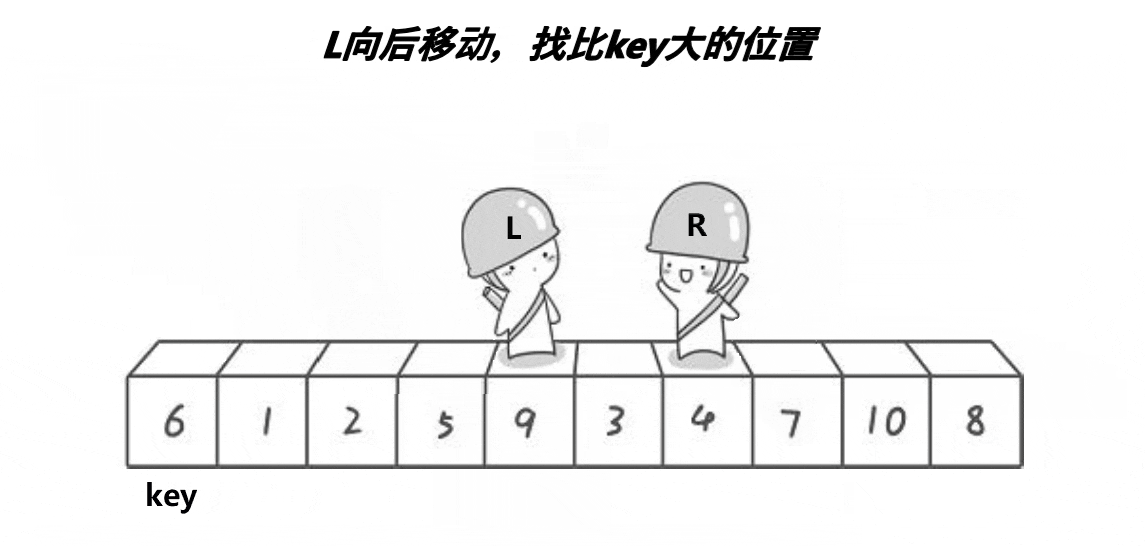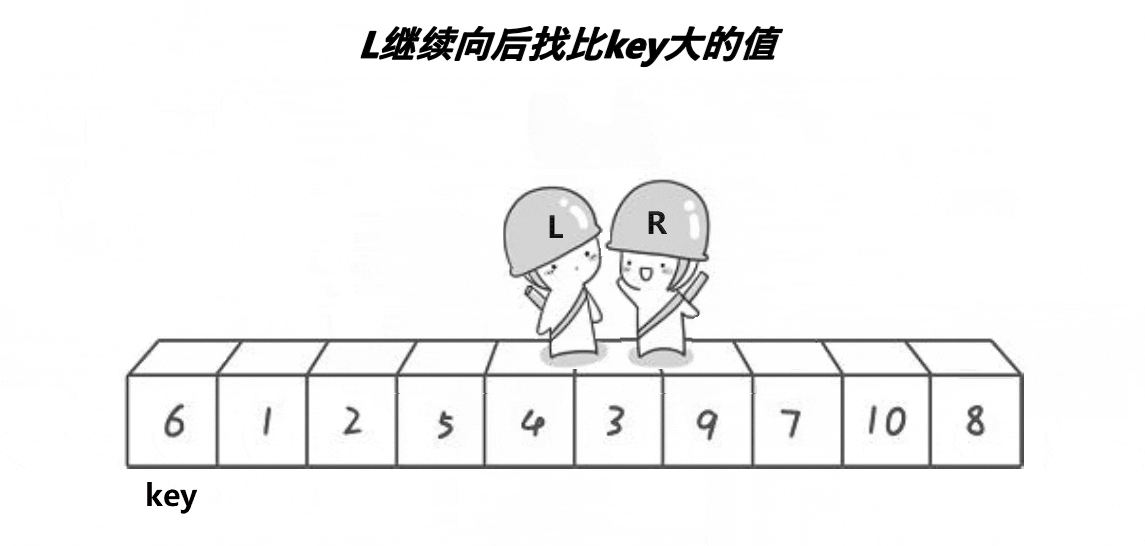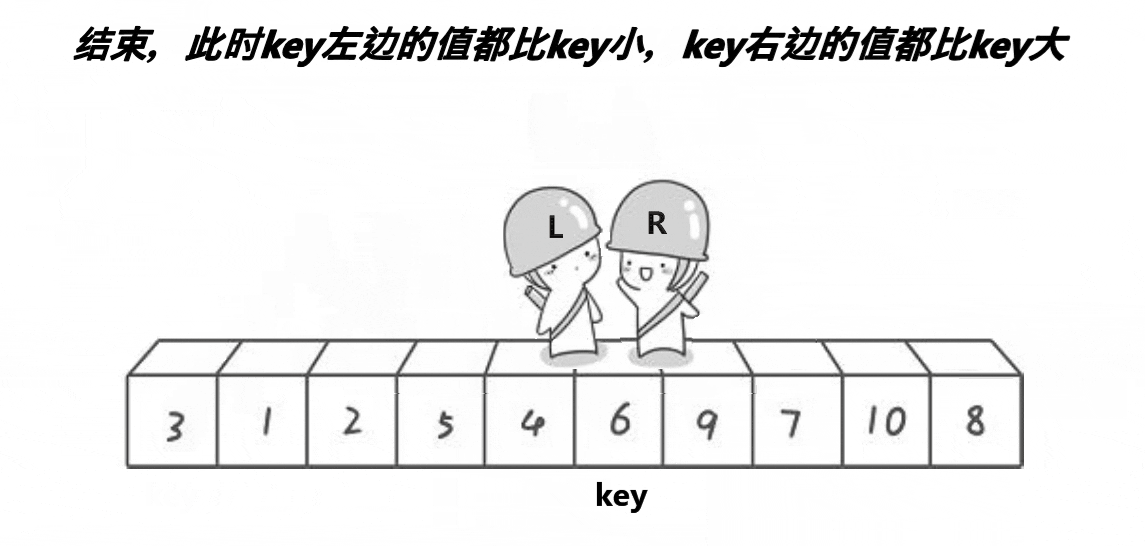
实现思路:
通过两个指针的移动,左边找大,右边找小,目的是让大的去到右边,小的去到左边,二者相遇再与 key 位置交换。记得 key 在哪边,对面的指针先动。否则会出现下面这个情况:

当两个指针发生交换时,左边指针会因为找到大的停下,右边再与左边的相遇,那么这个元素较大;如果右边先走,那么交换之后,右边找到的一定是小的,相遇时也能保证是小的
单趟实现:
左边找大,右边找小,相遇则交换 key 的位置元素
整体实现:
此时需要更新 key 的位置到二者相遇的位置,然后就将数组分为了两组,分别递归,例如:


记录的原因以及递归的过程:
如果不记录left、right ,那么递归右区间时,right会随着左递归不断变化,导致无法递归右区间

cpp
//Hoare排序
void Hoare(int* arr,int left,int right,int size)
{
//递归结束条件
if (left >= right)
{
return;
}
//记录
int begin = left;
int end = right;
//单趟
//设置key
int key = left;
while (left < right)
{
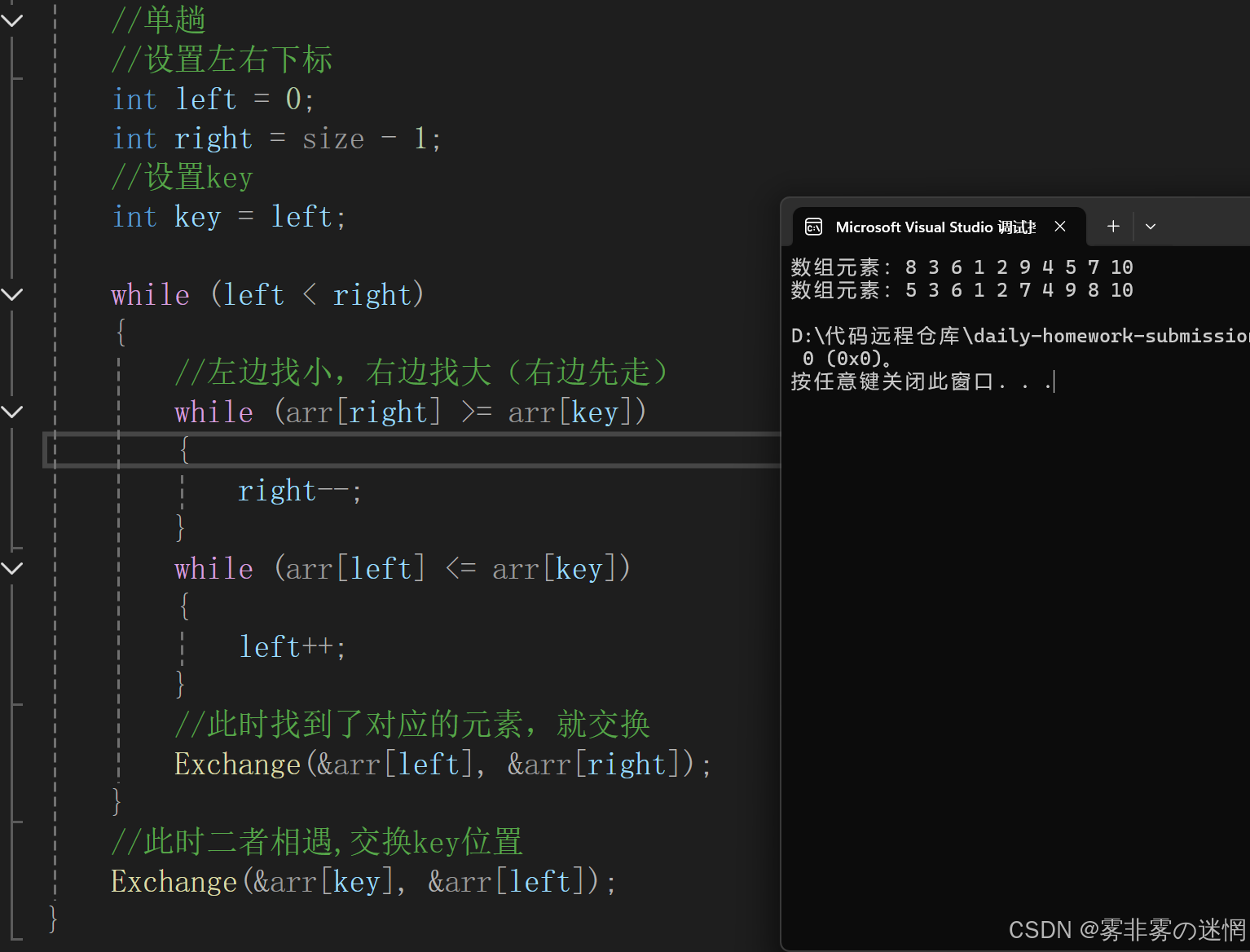
//左边找小,右边找大(右边先走)
while (arr[right] >= arr[key] && left < right)
{
right--;
}
while (arr[left] <= arr[key] && left < right)
{
left++;
}
//此时找到了对应的元素,就交换
Exchange(&arr[left], &arr[right]);
}
//此时二者相遇,交换key位置
Exchange(&arr[key], &arr[left]);
key = left;
//左递归
Hoare(arr, begin, key - 1, size);
//右递归
Hoare(arr, key + 1, end, size);
}复杂度:
时间复杂度:O(N logN),空间复杂度:O(1)
快排(双指针)
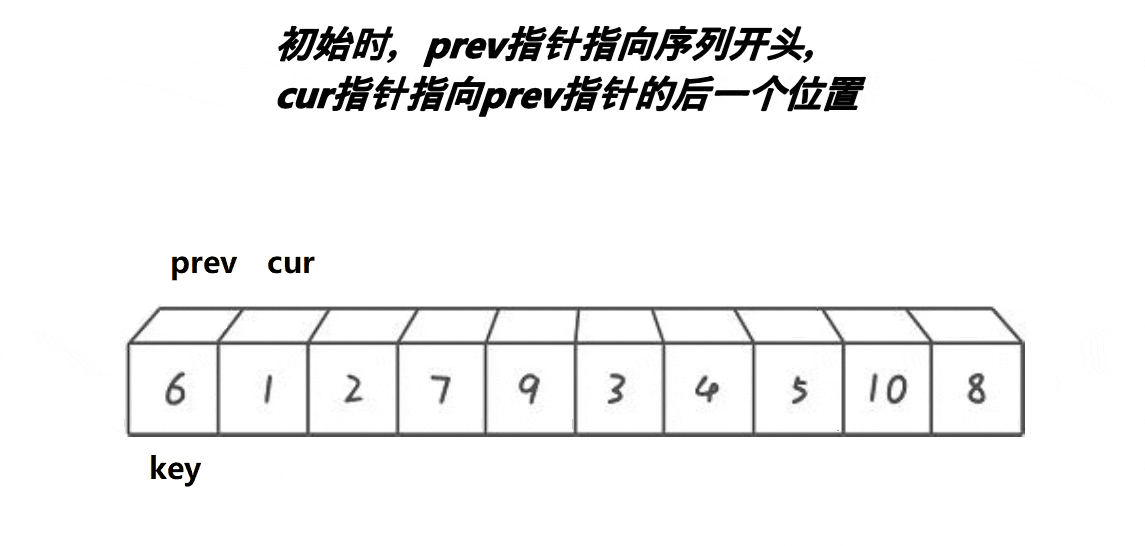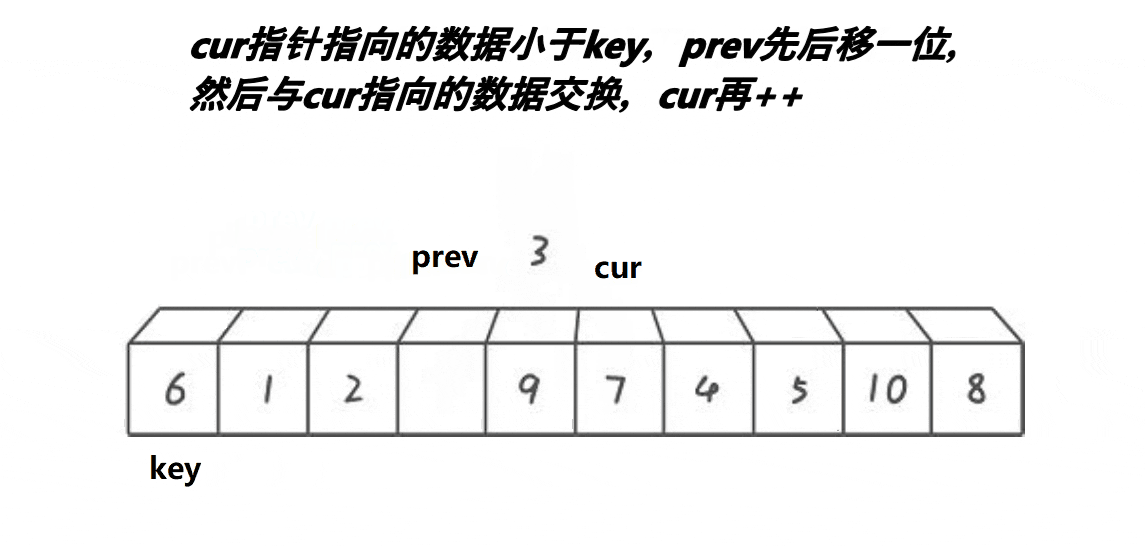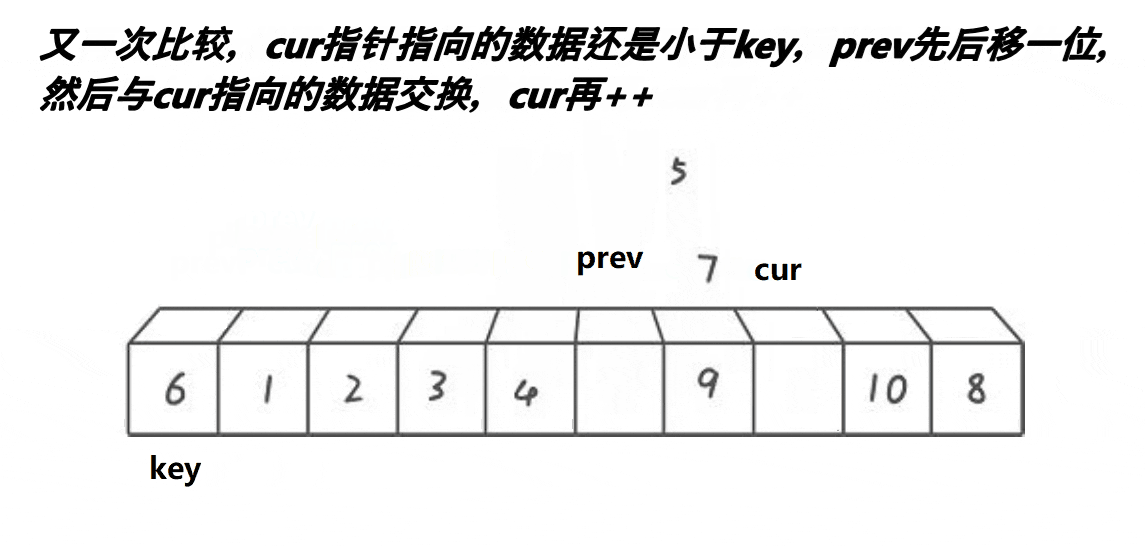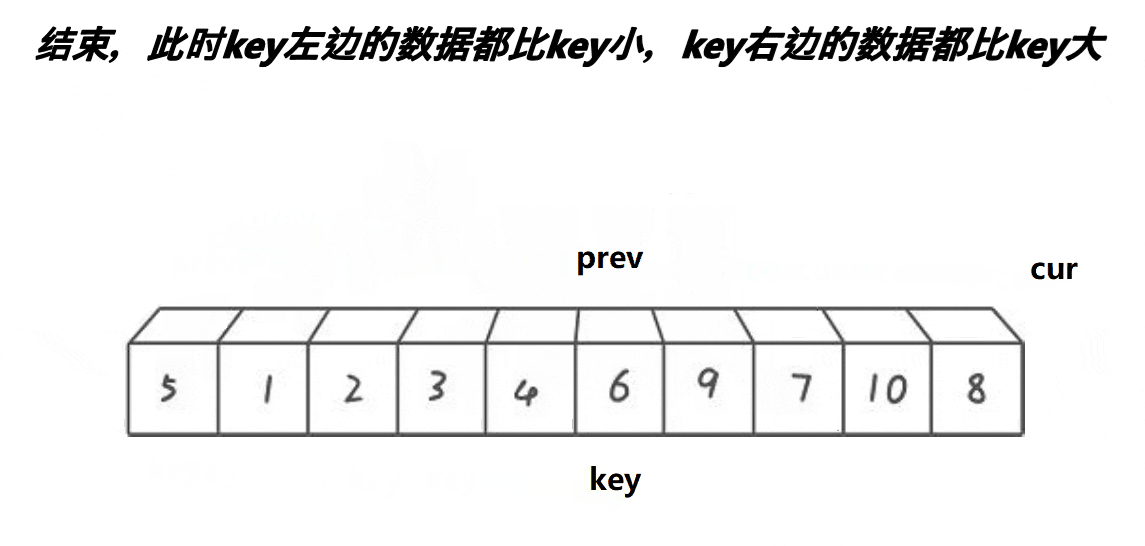
实现思路:
单趟: 
开始时有两个指针 prev 与 cur ,分别找大找小,随后进行交换。注意交换完之后,cur需要移动,否则一直进不了循环(单趟是排完一个数字)

整体实现:
现在我们划分了基准值,分别递归左、右区间,注意记录部分值,原因和Hoare排序一样

cpp
//快排(双指针)
void Snap_shot(int* arr, int size,int prev)
{
//断言
assert(arr);
int cur = prev + 1;
//递归结束条件
if (cur >= size)
{
return;
}
//记录
int begin = prev;
//设置基准值
int pivot = prev;
while (cur < size)
{
//找小找大,注意是cur先动
while (arr[cur] >= arr[pivot] && cur < size)
{
cur++;
}
while (arr[prev] <= arr[pivot] && prev < cur && cur < size)
{
prev++;
}
if (cur < size)
{
//此时找到了对应的值,进行交换
Exchange(&arr[cur], &arr[prev]);
//交换之后,cur再++
cur++;
}
}
//此时交换prev与pivot的位置
Exchange(&arr[prev], &arr[pivot]);
//更新基准值
pivot = prev;
//递归左区间(注意此时划分区间需要改变size)
Snap_shot(arr, pivot, begin);
//递归右区间
Snap_shot(arr, size, pivot + 1);
}复杂度:
时间复杂度:O(N logN),空间复杂度:O(1)
归并排序
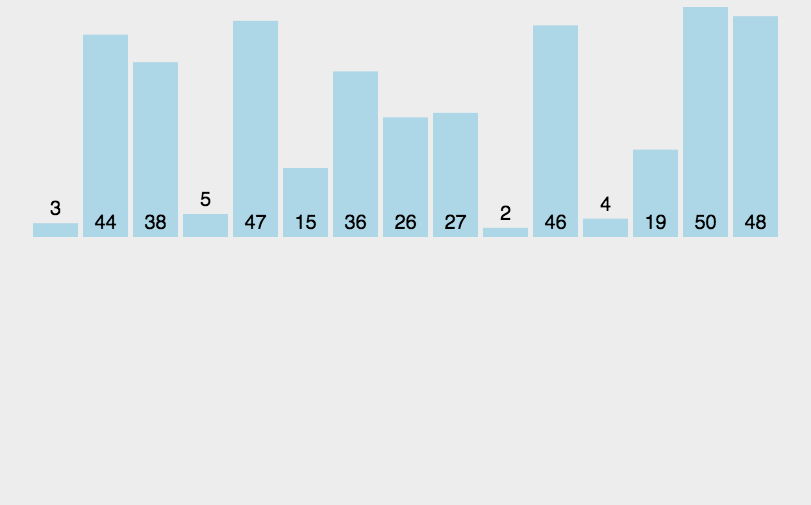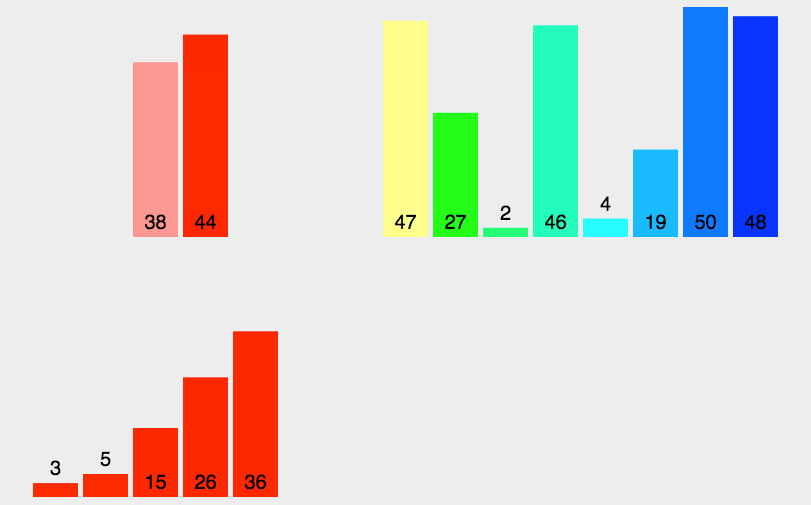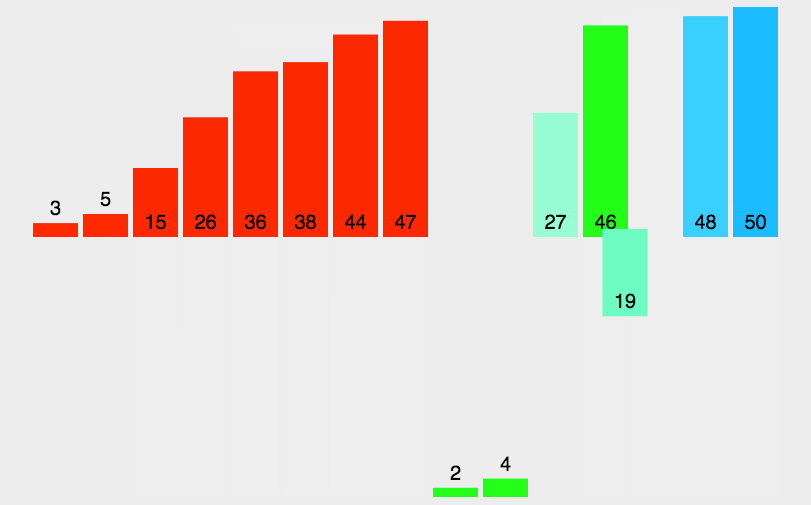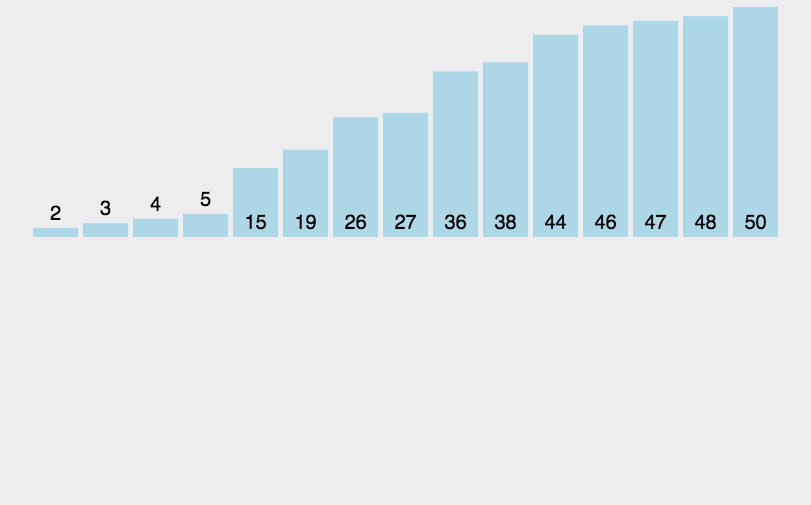
实现思路:


首先咱们看到这是将一个数组每次递归二分,这里通过划分区间并不难,难的是合并时如何排序?
建议一个临时数组,通过每次函数返回的基准值进行划分区间,当划分到左右区间只有一个数据时开始合并,合并时就需要去排序了【由于是复习文章,详细思路可看小编的主页【排序终结篇】】
递归分组:
左区间不断随着Middle分半,右区间会随着左区间传的参数改变left、right来产生,右边同理

cpp
//递归结束条件
if (left >= right)
{
return;
}
//划分
int Middle = (left + right) / 2;
//递归划分区间
//左区间
Sort(arr, newnode, left, Middle);
//右区间
Sort(arr, newnode, Middle + 1, right);归并过程:
此时我们划分了左右区间,分别是

然后我们对这个区间进行排序,排序的结果先放在临时数组,例如:8、3、6、1、2拷贝的例子:
我们可以用memcpy一键拷贝,需要注意它的三个参数:目的地起始位置、源起始位置、字节

主函数:
cpp
//归并排序
void Merge(int* arr,int size)
{
assert(arr);
//开辟空间
int* newnode = (int*)malloc(sizeof(int) * size);
if (newnode == NULL)
{
printf("空间开辟失败\n");
return;
}
//将开好的空间传给子函数
Sort(arr, newnode, 0, size - 1);
}子函数(递归、合并函数):
cpp
//归并子函数
void Sort(int* arr, int* newnode, int left, int right)
{
//递归结束条件
if (left >= right)
{
return;
}
//划分
int Middle = (left + right) / 2;
//递归划分区间
//左区间
Sort(arr, newnode, left, Middle);
//右区间
Sort(arr, newnode, Middle + 1, right);
//此时区间划分完毕,进行归并
int begin1 = left;
int end1 = Middle;
int begin2 = Middle + 1;
int end2 = right;
int tmp = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
//转移到新数组
newnode[tmp] = arr[begin1];
begin1++;
tmp++;
}
else
{
newnode[tmp] = arr[begin2];
begin2++;
tmp++;
}
}
//此时如果有元素未拷贝完,拷贝完剩余部分数据
while (begin1 <= end1)
{
newnode[tmp] = arr[begin1];
begin1++;
tmp++;
}
while (begin2 <= end2)
{
newnode[tmp] = arr[begin2];
begin2++;
tmp++;
}
//拷贝回原数组(注意left、right是下标,所以加一)
memcpy(arr+left, newnode+left, sizeof(int) * (right - left + 1));
}复杂度:
时间复杂度:O(N logN),空间复杂度:O(N)
排序OJ题(1)

快排采用找基准值,划分区间进行递归排序,为分治思想
排序OJ(2)

注意是从后往前比较。
假设此时排序完前7个元素:15、23、38、54、60、72、96 现在将45插入其中
45 VS 96 继续比较直到比到 38, 45>38,停止比较,中间有4个元素加上38一共比较了5次
此题何为从后往前:
例如第一个54已经为有序,现在插入38
38<54,有序组变为 38、54,继续下一个元素,意思是前7个正常排,45采用从后往前排
排序OJ(3)

归并需要额外开辟一个数组作为临时数组
排序OJ(4)

稳定排序的有: 冒泡、直接插入、归并
时间复杂度稳定在O(N^2)的只有直接插入排序
排序OJ(5)

两个指针分别找大找小再交换、最后找大的指针指向的元素与基准值65交换,得到A

【雾非雾】期待与你的下次相遇!