
文章目录
矩阵的转置

转置性质
(1)
(2)
(3)
(4)注意这个: 
扩展:
(5)
对称矩阵与反对称矩阵
对称矩阵:

结论:
(1)如果A,B同阶对称阵,那么A+B,A-B也是对称矩阵
(2)如果A是对称矩阵,那么kA,A的m次方也对称
(3)A,B同阶对称阵,AB对称;充要条件:AB=BA
(4)
反对称矩阵:

(1)A,B同阶反对称,那么A+B,A-B为反对称
(2)如果A反对称,则kA为反对称矩阵
(3)如果A反对称,则A的k次方:如果k为偶数,则对称,k为奇数则反对称
方阵的行列式

性质:
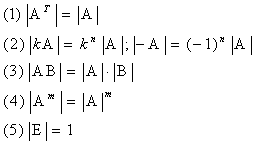
例题:


方阵的伴随矩阵(重要)
按行求,按列放

概念:

性质:


观看笔记来源: 《线性代数》教学视频 宋浩老师(2024年更新)