Missashe线代题型总结

Missashe线性代数考研题型总结

说明：这篇笔记用于博主对"线代"常考题型进行总结，99%为真题，大概可能应该会逐步更新解题思路。有目录可直接检索。

第一章 行列式

1 具体行列式计算

1）么字型

• 2015 数一

• 2016 数一三

2）X型

• 1996 数一

• 2014 数一二三
  

3）范德蒙

• 例1

• 例2

• 例3

• 例4

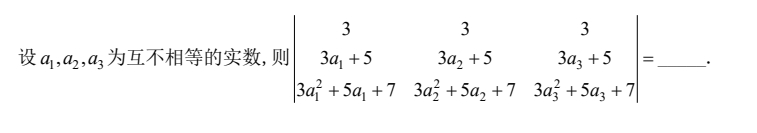
4）行和/列和相等

• 1988 数三

• 2020 数一二三

5）爪型

• 例1

6）其他

• 例1
• 例2

7）三对角行列式

• 例1

2 （代数）余子式相关

1）（代数）余子式求和

• 2019 数二

• 2021 数一

2）给出余子式相关信息定参

• 2024 数三
  

3 行列式形式的多项式 f ( x ) f(x) f(x)

1）确定 f ( x ) f(x) f(x)中 x x x某次方的系数

• 2021 数二三

2） f ( x ) = 0 f(x)=0 f(x)=0根的个数

• 1999 数二

4 抽象行列式计算（最重要）

• 1987 数一

• 1988 数一

• 1988 数三

• 1992 数三

• 1995 数一

• 1999 数一
  

• 2000 数三

• 2003 数二

• 2004 数一二

• 2005 数一二

• 2006 数一二三

• 2008 数三

• 2010 数二三

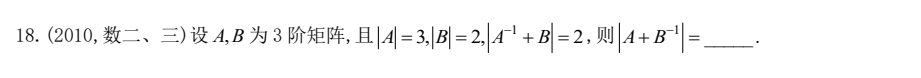
• 2012 数二三

• 2015 数二三

• 2018 数一

• 2018 数三

• 2023 数二三

• 2024 数三

5 Cramer法则（不重要）

第二章 矩阵

1 逆

1）具体矩阵求逆

• 1988 数三

• 1989 数一

• 1991 数一

• 1994 数三

• 1995 数三

2）抽象逆相关

• 2000 数二

• 2001 数一

• 2022 数一

3）（不）可逆的判定与证明

• 1990 数三

• 1996 数一

• 1997 数一

• 1997 数三

• 2002 数二

• 2008 数一二三
  

• 2017 数一三

2 伴随矩阵

1）伴随性质

• 1996 数三

• 1998 数二

2）伴随等于转置或本身

• 1994 数一

• 2005 数三

• 2013 数一二三

3 秩

1）求秩及证明秩

• 1987 数三

• 1990 数一

• 1992 数一

• 1993 数三

• 1994 数三

• 1995 数三
  

• 1996 数一

• 2007 数一二三

• 2008 数一

• 2010 数一二三

• 2012 数一

• 2017 数一三

• 2019 数二三

2）已知秩确定参数

• 1997 数二

• 1998 数三

• 2001 数三

• 2003 数三

3）利用秩推理

• 例1

4 高次幂

• 1988 数一

• 1992 数一

• 1994 数一

• 1999 数三

• 2000 数一
  

• 2024 数一

• 2016 数一二三

5 初等变换和初等矩阵

• 1995 数一
  

• 2001 数三

• 2004 数一二

• 2005 数一二

• 2006 数一二三

• 2009 数二三

• 2011 数一二三

• 2020 数一

• 2021 数二三

• 2022 数二三
  

• 2024 数二三

6 分块矩阵

1）分块矩阵的逆和伴随

• 1991 数三

• 2009 数一二三

• 2023 数二三

2）分块矩阵的秩

• 2018 数一二三

• 2021 数一

• 2023 数一
  

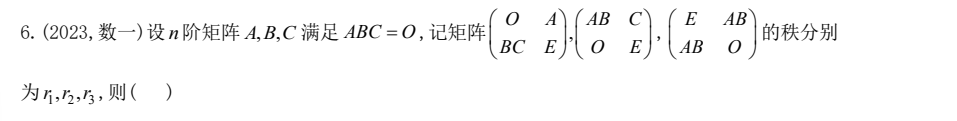
7 AB=口

1） A B = E AB=E AB=E

• 1991 数一

2） A B = 0 AB=0 AB=0

• 1993 数一

• 1988 数三

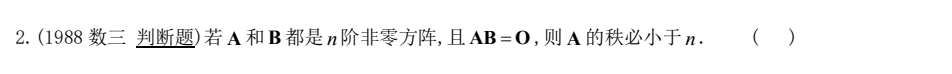
• 1997 数一

• 1998 数三

• 2004 数一二

• 2024 数二

3） A B = C AB=C AB=C

• 2013 数一二三

8 矩阵分解

1）正定矩阵的分解

• 2021 数一

9 其他题型

1）求各行/列元素之和

• 例1

2）矩阵等价

• 1997 数三

• 2004 数三

• 2016 数二

3）已知 A B AB AB求 B A BA BA（不看）

4）矩阵化E

• 1995 数三

5） A B = B A AB=BA AB=BA

• 例1
• 例2

6）正交矩阵（不看）

7）给出矩阵等式推导相关结论

• 例1

8）反对称矩阵

• 例1

9）直接考察秩为一

• 2003 数二

10）简单性质考察

• 1989 数一三

• 1989 数三
  

第三章 向量

1 向量有关计算

• 2021 数一

• 2023 数一

• 2024 数一

2 线性表示

1）线性表示的判定

• 1992 数一

2）根据线性表示情况确定参数并将向量线性表示

• 1991 数一

• 1991 数三

• 1998 数二
  

• 2000 数二

• 2000 数三

• 2004 数三

• 2005 数二

• 2011 数一二

• 2019 数二三

3）根据线性表示推理

• 1999 数三

• 2002 数二

• 2003 数一二

• 2010 数二三

4）共同线性表示

• 2023 数一二三

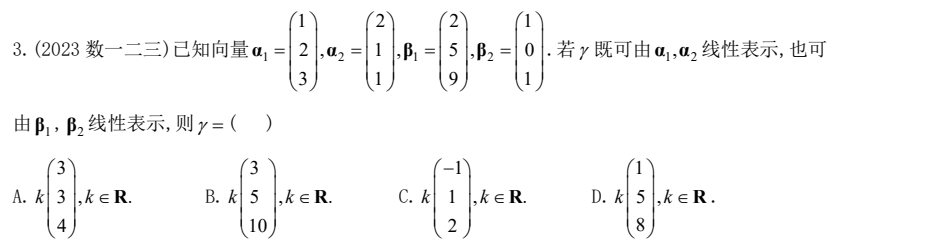
3 向量组等价

• 2022 数一二三

4 线性相关与无关

1）线性相关无关概念

• 1996 数三

• 1987 数三

• 1988 数一
  

• 1990 数三

• 2003 数三

• 2000 数一

• 2005 数一二三

2）讨论相关无关

• 1988 数三

• 1989 数三

• 1999 数二

• 2006 数三

3）证明线性无关

• 1991 数三

• 1993 数一

• 1996 数三

• 1998 数一

• 2008 数二三

4）根据相关无关确定参数

• 2002 数三

• 2005 数三

• 2012 数一二三

• 2024 数一

• 2024 数二

5）多个向量组相关无关的关系

• 1994 数一

• 1997 数三

• 2007 数一二三

• 2006 数一二三

• 2014 数一二三

第四章 方程组

1 解的判定

1）判断解的情况

• 1992 数三

• 2001 数三

• 2002 数三

• 2022 数二三

2）已知解的情况确定参数

• 1992 数三

• 1989 数三

• 1990 数三

• 2000 数一

• 2001 数二

• 2015 数一二三

• 2019 数三

2 方程组求解

1）齐次

（1）具体矩阵

• 1998 数一

• 2002 数三

• 2003 数三

• 2004 数一

• 2004 数二

（2）抽象矩阵

①求基础解系中向量个数

• 2004 数三

②求基础解系/通解

• 1993 数一

• 2005 数一二

• 2011 数一二
  

• 2020 数二三

• 2019 数一

③已知若干齐次解，判断其他向量是否为齐次解

• 例1

④已知一个基础解系，证明另一个向量组为基础解系

• 2001 数一二三

• 2001 数二

⑤已知一个基础解系，求另一个基础解系

• 例1

2）非齐次

（1）具体矩阵

• 1987 数一

• 1987 数三

• 1988 数三

• 1989 数一

• 1990 数三

• 1993 数三

• 1994 数三

• 1996 数三

• 1997 数二

• 2000 数二

• 2006 数一二

• 2008 数一二三

• 2009 数一二三

• 2010 数一二三

• 2012 数一二三
  

• 2016 数二三

（2）抽象矩阵

①非齐次方程组线性无关解向量的个数

• 2004

②已知解向量求通解

• 1990 数一

• 2011 数三

③已知向量关系求通解

• 2002 数一二三

• 2017 数一二三

④已知解向量的线性组合求通解

• 2000 数三

⑤已知特征求通解

• 例1

⑥已知一方程组通解，求另一方程组通解

• 例1
• 例2

⑦根据其他已知条件求通解

• 2021 数三
  

⑧找一个非齐次特解

• 例1

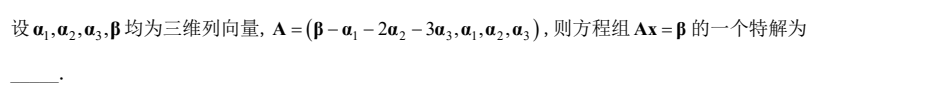
⑨求非齐次方程组的唯一解

• 例1

3 已知方程组的解推导其他

• 1992 数一

4 解的关系

1）公共解

（1）已知[I][II]具体形式

• 2007 数一二三

（2）已知[I]通解[II]具体形式

• 1994 数一

（3）已知[I][II]通解

• 例1

（4）[I][II]抽象

• 例1

2）同解

（1）同解判断

• 2000 数三
  

• 2022 数一

（2）已知同解反求参数并求同解X

• 2005 数三

（3）同解充要

• 例1

（4）证明（不看）

3）两个方程组其他解的关系

• 2003 数一

• 2021 数二

• 2024 数二

• 2024 数三

5 矩阵方程

1）二阶

• 2013 数一二三

2）可逆

• 1987 数一

• 1987 数三

• 1995 数一

• 1989 数三

• 1990 数一

• 1997 数二

• 1998 数二

• 1999 数二

• 1998 数三

• 2000 数一

• 2001 数二

• 2002 数二

• 2015 数二三

3）不可逆

（1）不含参数直接解

• 2014 数一二三

（2）含参数讨论完再解

• 2016 数一

（3）求可逆的矩阵

• 2018 数一二三

4）其他情况

• 2001 数一

第五章 特征值与特征向量

1 特征值特征向量

1）求特征值特征向量

（1）具体矩阵

• 2002 数二

• 2003 数一

（2）抽象矩阵

• 1987 数三

• 1989 数三

• 1991 数三

• 1998 数一

• 1998 数三

• 1999 数一

• 1999 数一三

• 2002 数三
  

• 2002 数三

• 2008 数二

• 2008 数一

• 2009 数一

• 2018 数二

• 2024 数一

2）特征相关证明

• 1990 数三

• 1989 数一

3)特征相关推理

• 2017 数二

2 相似

1）根据相似确定参数或推理

• 1999 数三

• 2009 数二

• 2009 数三

2）判断相似

• 2010 数一二三

• 2013 数一二三

• 2016 数一

• 2017 数一二三

• 2018 数一二三
  

3）求可逆矩阵P,使得 P − 1 A P = B P^{-1}AP=B P−1AP=B

• 1992 数三

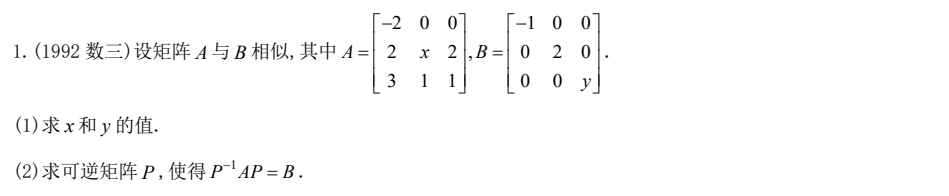
• 1988 数一

• 2019 数一二三

4）相似相关证明

• 2002 数一

• 2014 数一二三

3 相似对角化

1）相似对角化概念

• 2012 数一二三
  

• 2017 数二

• 2020 数二三

2）可相似对角化相关讨论及证明

• 1994 数三

• 2004 数一二

3）相似对角化充要条件

• 1993 数三

• 2022 数一

• 2022 数二三

• 2024 数二

4）判断是否可以相似对角化

• 1997 数一

• 2020 数一二三

• 2023 数一

5）求相似对角化的可逆阵P及对角阵Λ

• 2003 数二

• 2004 数三

• 2015 数一二三

• 2021 数二三

• 2023 数二三

4 实对称矩阵

1）实对称矩阵相关推理

• 例1

2）求正交矩阵Q

（1）常规三阶题

• 2001 数三

• 2006 数一二

• 2006 数三

• 2010 数二三

（2）四阶题

• 1996 数三

（3）两个矩阵同时正交相似对角化

• 例1
  

3）求实对称矩阵A

• 1995 数一

• 1997 数三

• 2007 数一二三

• 2010 数一

• 2011 数一二三

第六章 二次型

1 二次型的秩或矩阵

• 2004 数三

2 标准型

1）可逆变换 x = P y x=Py x=Py

• 例1

2）正交变换 x = Q y x=Qy x=Qy

• 1990 数一

• 1993 数一

• 1993 数三
  

• 1995 数三

• 2002 数一

• 2003 数三

• 2011 数三

• 2012 数一二三

• 2013 数一二三

• 2015 数一二三

• 2017 数一二三

• 2024 数三

3）可逆+正交

• 例1
  

3 规范型

• 2001 数三

• 2009 数一二三

• 2019 数一二三

• 2023 数二三

4 一个二次型变成另一个二次型，求变换矩阵

1）可逆变换求变换矩阵

• 2020 数二

2）正交变换求变换矩阵

• 2020 数一三

3）普通+正交变换求变换矩阵

• 2023 数一

5 求二次型的解

• 2005 数一

• 2018 数一二三

• 2022 数一

6 求二次型最值

• 2022 数二三

7 求可逆阵，使得 A = P T E P A=P^TEP A=PTEP

• 例1

8 正负惯性指数

1）求正负惯性指数

• 2011 数二

• 2021 数一二三
  

2）已知正负惯性指数信息确定参数或其他

• 2014 数一二三

• 2016 数二三

9 合同

• 2001 数一

• 2007 数一二三

• 2008 数二三

10 正定

1）已知正定反求参数

• 1997 数三

• 1998 数三

• 1999 数一

• 1999 数三

• 2000 数三

2）正定相关证明

• 1991 数一

• 1991 数三

• 1992 数三

• 2005 数三

3）其他

• 例1
• 例2