一、标量
标量(Scalar) 是一种仅用数值大小(即 "量值")就能完全描述的物理量或数学对象,它不具有方向属性。
例如在实数领域的正数、负数。
在物理学领域的多少斤、多少公斤、水温多少度、气温多少度都是标量。
因此标量的无方向并非无意义的,它实际上侧重于强调数量上的多少。
二、矢量
矢量,也称向量(Vector) 是一种既具有大小 又具有方向的量,它的完整描述必须同时包含这两个要素。
例如:在生活中的向东100KM/H,垂直向下的力"5 牛顿。在力学中常见的有位移(s),速度(v)、加速度(a)、力(F),电磁学中电场强度(E)、磁感应强度(B)、电流密度(j)。
矢量常用带箭头的字母(如 v)或黑体字母(如 F)表示,其大小称为模长(记作 ∣v∣ 或 v),方向则由空间中的指向确定。
三、矩阵

矩阵(Matrix) 是一种由数排列成的矩形阵列,用于系统地表示和处理线性方程组、变换和数据。
例如,生活中的Excel表格,编程关系型数据库中一张张实体表,都可看着矩阵。
矩阵是由 m×n 个数排成的 m 行(Row)n 列(Column)的矩形表格,记作 A 或 [aij],其中 aij 表示第 i 行第 j 列的元素。
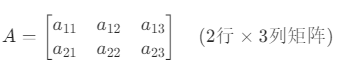
四、要点辨析
行向量: 数字排成一行,用括号括起来。例如小明语数外成绩(96,91,99)
列向量: 把数字排成一列,用括号括起来。例如二维平面上的点坐标(x,y),写成列向量就是 (x,y)。
上面两个用二维表格来形容,行向量适合按 "顺序" 记录一排数据,列向量适合按 "类别" 堆叠信息。
注意:编程中的数据一般用 [1, 2, 3],也就是中括号括起来,而向量一般用小括号括起来。
根据以上辨析,可以看出,矩阵可以看着是由若干个行向量或若干个列向量构成的集合。
在学校教室里的班级看着是一个矩阵的话,那么可理解为若干排同学或若干列同学构成了这个班级。
五、两种视角的意义
**行向量视角:**适合看 "每行的独立信息",比如矩阵的每一行代表一个样本(如每个学生的各科成绩);
**列向量视角:**适合看 "每列的特征",比如矩阵的每一列代表一个科目,所有列向量组成该科目的成绩集合。