数学笔记三：特殊矩阵

一、单位矩阵

• 定义 ：主对角线元素全为 1，其余元素全为 0 的方阵，。
• 性质：对任意矩阵 A（满足维度兼容），有 AI=A，IA=A，类似数的 "1"。

二、逆矩阵（仅针对可逆方阵）

1. 定义

• 若方阵 A 存在矩阵 ，使得 A=A=I（I 为单位矩阵），则 称为 A 的逆矩阵。
• 条件 ：∣A∣0（非奇异矩阵）。

2. 性质

三、矩阵的转置

1. 定义

• 将矩阵 A 的行列互换，得到的新矩阵称为 A 的转置，记作 或 A′。
• 若 A 是 m×n 矩阵，则 是 n×m 矩阵。

2. 示例

3. 性质

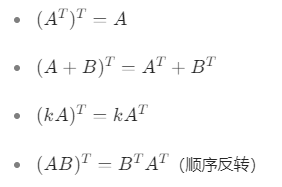
四、矩阵的行列式（仅针对方阵）

1. 定义

• 对于 n×n 方阵 A，其行列式记作 ∣A∣ 或 det(A)，是一个数值，反映矩阵的某些性质（如可逆性）。

2. 计算示例（二阶方阵）

3. 性质

• ∣∣=∣A∣
• ∣AB∣=∣A∣∣B∣