自然语言处理——文本表示

自然语言处理------文本表示

• 词语的表示学习
• • [C&W model](#C&W model)
  • [CBOW model](#CBOW model)
  • [Skip-gram model](#Skip-gram model)
  • GloVe
  • 字-词混合的表示学习
• 短语的表示学习
• • 词袋方法
  • 递归自动编码器
  • 双语约束模型
• 句子的表示学习
• • 词袋方法
  • PV-DM模型
  • PV-DBOW模型
  • Skip-Thought模型
  • CNN模型
• 文档的表示学习
• • 词袋方法
  • 层次化模型

目前关于文本表示模型主要有以下两种：

• 文本概念表示模型：以（概率）潜在语义分析（Latent Semantic Analysis, LSA）和潜在狄利克雷分布（Latent Dirichlet allocation, LDA）为代表的主题模型，旨在挖掘文本中的隐含主题或概念，文本将被表示为主题的分布向量
• 深度表示学习模型：通过深度学习模型以最优化特定目标函数（例如语言模型似然度）的方式在分布式向量空间中学习文本的低维实数向量表示

词语的表示学习

词语通常表示为词向量，称为look_up_table,我们可以对𝐿右乘一个词的one-hot表示𝑒得到该词的低维、稠密的实数向量表达：𝑥=𝐿e

词表规模𝑉和词向量维度𝐷如何确定？

• 𝑉的确定：1. 训练数据中所有词；2.频率高于某个阈值的所有词；3.前V个频率最高的词
• 𝐷的确定，超参数由人工设定，一般从几十到几百

学习L时，通常先随机初始化，然后通过目标函数优化词的向量表达（e.g. 最大化语言模型似然度）

C&W model

C&W model的核心思想就是随机替换：将句子中的一个词随机替换成另外一个词，如果替换之前的得分高于替换之后的得分，说明原方案更好，不需要替换。这样子就可以通过上下文表示来学习中间单词的表示。

这个损失函数的目标是：

• 最大化正样本的得分： 对于真实的词-上下文对 ( w i , C ) (w_i ,C) (wi,C)，模型应该给出一个高分。
• 最小化负样本的得分： 对于随机的、不相关的词-上下文对 ( w i ′ , C ) (w_i' ,C) (wi′,C)，模型应该给出一个低分。
• 强制边际分离： 更重要的是，它强制正样本的得分 score ( w i , C ) (w_i ,C) (wi,C) 至少要比负样本的得分 score ( w i ′ , C ) (w_i' ,C) (wi′,C) 大一个预设的边际（这里是 1）。如果这个条件不满足，就会产生损失，模型就会进行调整，使得正样本的得分更高，负样本的得分更低。

CBOW model

CBOW model即词袋模型，不考虑词序的影响，基于周围的上下文来预测中间的单词，当然这边其实可以理解为一个softmax的过程，得到概率最大的单词。

Skip-gram model

不同于CBOW模型利用上下文词语预测中心词语，Skip-gram模型采用了相反的过程，即采用中心词语预测所有上下文词语。

给定训练语料中任意一个n-元组 ( 𝑤 𝑖 , 𝐶 ) = 𝑤 𝑖 − 𝐶 ⋯ 𝑤 𝑖 − 1 𝑤 𝑖 𝑤 𝑖 + 1 ⋯ 𝑤 𝑖 + 𝐶 (𝑤_𝑖,𝐶)= 𝑤_{𝑖−𝐶} ⋯𝑤_{𝑖−1}𝑤_𝑖𝑤_{𝑖+1}⋯𝑤_{𝑖+𝐶} (wi,C)=wi−C⋯wi−1wiwi+1⋯wi+C，Skip-gram模型直接利用中心词语 w i w_i wi的词向量𝑒( 𝑤 𝑖 𝑤_𝑖 wi)预测上下文 w c = 𝑤 𝑖 − 𝐶 ⋯ 𝑤 𝑖 − 1 𝑤 𝑖 + 1 ⋯ 𝑤 𝑖 + 𝐶 w_c=𝑤_{𝑖−𝐶}⋯𝑤_{𝑖−1}𝑤_{𝑖+1}⋯𝑤_{𝑖+𝐶} wc=wi−C⋯wi−1wi+1⋯wi+C中每个词语 𝑤 𝐶 𝑤_𝐶 wC的概率:
P ( w C ∣ w i ) = exp ⁡ { e ( w i ) ⋅ e ( w C ) } ∑ k = 1 ∣ V ∣ exp ⁡ { e ( w i ) ⋅ e ( w k ) } P\left(w_{C} \mid w_{i}\right)=\frac{\exp \left\{e\left(w_{i}\right) \cdot e\left(w_{C}\right)\right\}}{\sum_{k=1}^{|V|} \exp \left\{e\left(w_{i}\right) \cdot e\left(w_{k}\right)\right\}} P(wC∣wi)=∑k=1∣V∣exp{e(wi)⋅e(wk)}exp{e(wi)⋅e(wC)}

L ∗ = argmax ⁡ L ∑ w i ∈ V ∑ w C ∈ W C log ⁡ P ( w C ∣ w i ) L^{*}=\underset{L}{\operatorname{argmax}} \sum_{w_{i} \in V} \sum_{w_{C} \in W C} \log P\left(w_{C} \mid w_{i}\right) L∗=Largmaxwi∈V∑wC∈WC∑logP(wC∣wi)

思考：CBOW和Skip-gram缺陷

• C的大小限制
• 难以解决多义词的问题
• 没有考虑跨样本的情况（需要考虑全局）

GloVe

C&W模型、CBOW以及Skip-gram模型都是采用局部上下文信息，没有用到语料的整体分布信息

GloVe (Global Vectors for Word Representation) 模型旨在同时充分利用局部上下文信息和语料的整体分布信息，其主要思想如下：

• 根据语料库构建一个共现矩阵，矩阵中的每一个元素 𝑋 𝑖 𝑗 𝑋_{𝑖𝑗} Xij代表单词𝑗在单词𝑖特定大小的上下文窗口内共同出现的次数（即在整个语料库当中的出现次数）
• 构建词向量，目标使得词向量之间的关系能够反映共现矩阵之间的关系

𝑋 𝑖 𝑗 𝑋_{𝑖𝑗} Xij表示单词𝑗出现在单词𝑖的上下文的次数；
X 𝑖 X_𝑖 Xi表示单词𝑖的上下文中所有单词出现的总次数，即 𝑋 𝑖 = ∑ k X i k 𝑋_𝑖=\sum_kX_{ik} Xi=∑kXik；
P 𝑖 𝑗 = P ( 𝑖 ∣ 𝑗 ) = 𝑋 𝑖 𝑗 / 𝑋 𝑖 P_{𝑖𝑗} = P(𝑖|𝑗) = 𝑋_{𝑖𝑗}/𝑋_𝑖 Pij=P(i∣j)=Xij/Xi 表示单词𝑗出现在单词𝑖的上下文中的概率；

e ( w i ) , e ( w j ) , e ( w ~ k ) e\left(w_{i}\right), e\left(w_{j}\right),e\left(\widetilde{w}{k}\right) e(wi),e(wj),e(w k)分别表示单词𝑖、单词𝑗、上下文单词的词向量表示
F ( e ( w i ) , e ( w j ) , e ( w ~ k ) ) = P i k P j k F ( e ( w i ) − e ( w j ) , e ( w ~ k ) ) = P i k P j k F ( ( e ( w i ) − e ( w j ) ) T e ( w ~ k ) ) = P i k P j k F ( e ( w i ) T e ( w ~ k ) − e ( w j ) T e ( w ~ k ) ) F ( e ( w i ) T e ( w ~ k ) ) F ( e ( w j ) T e ( w ~ k ) ) F\left(e\left(w{i}\right), e\left(w_{j}\right), e\left(\widetilde{w}{k}\right)\right)=\frac{P{i k}}{P_{j k}}\\F\left(e\left(w_{i}\right)-e\left(w_{j}\right), e\left(\widetilde{w}{k}\right)\right)=\frac{P{i k}}{P_{j k}}\\F\left(\left(e\left(w_{i}\right)-e\left(w_{j}\right)\right)^{T} e\left(\widetilde{w}{k}\right)\right)=\frac{P{i k}}{P_{j k}}\\F\left(e\left(w_{i}\right)^{T} e\left(\widetilde{w}{k}\right)-e\left(w{j}\right)^{T} e\left(\widetilde{w}{k}\right)\right)\\\frac{F\left(e\left(w{i}\right)^{T} e\left(\widetilde{w}{k}\right)\right)}{F\left(e\left(w{j}\right)^{T} e\left(\widetilde{w}_{k}\right)\right)} F(e(wi),e(wj),e(w k))=PjkPikF(e(wi)−e(wj),e(w k))=PjkPikF((e(wi)−e(wj))Te(w k))=PjkPikF(e(wi)Te(w k)−e(wj)Te(w k))F(e(wj)Te(w k))F(e(wi)Te(w k))

最终化简得到：F(a-b)=F(a)/F(b)，F可以认为是exp函数。将log x i x_i xi 设置为一个偏置项
F ( e ( w i ) T e ( w ~ k ) ) = P i k = X i k X i e ( w i ) T e ( w ~ k ) = log ⁡ ( P i k ) = log ⁡ ( X i k ) − log ⁡ ( X i ) e ( w i ) T e ( w ~ k ) + b i + b ~ k = log ⁡ ( X i k ) \begin{array}{c}F\left(e\left(w_{i}\right)^{T} e\left(\widetilde{w}{k}\right)\right)=P{i k}=\frac{X_{i k}}{X_{i}} \\ e\left(w_{i}\right)^{T} e\left(\widetilde{w}{k}\right)=\log \left(P{i k}\right)=\log \left(X_{i k}\right)-\log \left(X_{i}\right) \\ e\left(w_{i}\right)^{T} e\left(\widetilde{w}{k}\right)+b{i}+\tilde{b}{k}=\log \left(X{i k}\right)\end{array} F(e(wi)Te(w k))=Pik=XiXike(wi)Te(w k)=log(Pik)=log(Xik)−log(Xi)e(wi)Te(w k)+bi+b~k=log(Xik)

J = ∑ i , j = 1 V f ( X i j ) ( e ( w i ) T e ( w ~ j ) + b i + b ~ j − log ⁡ ( X i j ) ) 2 J=\sum_{i, j=1}^{V} f\left(X_{i j}\right)\left(e\left(w_{i}\right)^{T} e\left(\widetilde{w}{j}\right)+b{i}+\tilde{b}{j}-\log \left(X{i j}\right)\right)^{2} J=i,j=1∑Vf(Xij)(e(wi)Te(w j)+bi+b~j−log(Xij))2

字-词混合的表示学习

词语由字或字符构成，一方面词语作为不可分割的单元可以获得一个表示；另一方面词语作为字的组合，通过字的表示也可以获得一个表示；两种表示结合得到更优表示。

值得一提的是：在低维、稠密的实数向量空间中，相似的词聚集在一起，在相同的历史上下文中具有相似的概率分布！

短语的表示学习

词袋方法

假设短语由𝑖个词语构成，视短语为词袋，短语可以表示为词语向量的平均或者加权平均
e ( p h i ) = ∑ k = 1 i v k ⋅ e ( w k ) e\left(p h_{i}\right)=\sum_{k=1}^{i} v_{k} \cdot e\left(w_{k}\right) e(phi)=k=1∑ivk⋅e(wk)

但是这样子有一个问题：像"猫吃鱼"和"鱼吃猫"这两个短语明显是不同的意思，但是用该方法计算之后得到的是相同的词向量，这表示这个方法忽略了词序的影响。

递归自动编码器

模型通过递归的方式，将相邻或相关节点的表示合并成一个更高级的表示。同样的这一个高级的表示也需要重构出它是由那两个节点构成的，并且要求重构出来的词向量和原来的输入词向量相似，这一点在损失函数当中也可以看到，词向量相似只需要将两者的均方误差最小即可，这样子就考虑了词序的影响。

双语约束模型

假设已知 p h x , p h y ph_x,ph_y phx,phy是两种语言互为翻译的短语，那么理论上这两个短语的语义表示应该是一样的

句子的表示学习

词袋方法

假设句子由𝑛个词语构成，视句子为词袋，可以把句子表示为词语向量的平均或者表示为词语向量的加权平均。但是同样可能会有"猫吃鱼"和"鱼吃猫"一样的情况。

PV-DM模型

对于语料𝐷中的𝑀个句子，按照顺序，每个句子 𝑠 𝑖 𝑠_𝑖 si对应一个序号𝑖，该序号𝑖可唯一代表这个句子。假设我们希望句子向量的维度为p，那么训练集中所有句子的向量对应一个矩阵 𝑃 𝑉 ∈ R 𝑀 × 𝑝 𝑃𝑉∈ℛ^{𝑀×𝑝} PV∈RM×p。序号为𝑖的句子对应的向量是𝑃𝑉中的第𝑖行。

PV-DM模型（Paragraph Vector with sentence as Distributed Memory）是CBOW 的扩展 ，将上下文所在的句子视为一个记忆单元，对于任意一个𝑛-元组 ( 𝑤 𝑖 , 𝐶 ) = 𝑤 𝑖 − 𝐶 ⋯ 𝑤 𝑖 − 1 𝑤 𝑖 𝑤 𝑖 + 1 ⋯ 𝑤 𝑖 + 𝐶 (𝑤_𝑖,𝐶)=𝑤_{𝑖−𝐶}⋯𝑤_{𝑖−1}𝑤_𝑖𝑤_{𝑖+1}⋯𝑤_{𝑖+𝐶} (wi,C)=wi−C⋯wi−1wiwi+1⋯wi+C以及该𝑛-元组所在的句子序号𝑆𝑒𝑛𝐼𝑑，我们将𝑆𝑒𝑛𝐼𝑑和 w 𝐶 = 𝑤 𝑖 − 𝐶 ⋯ 𝑤 𝑖 − 1 𝑤 𝑖 + 1 ⋯ 𝑤 𝑖 + 𝐶 w_𝐶 =𝑤_{𝑖−𝐶}⋯𝑤_{𝑖−1}𝑤_{𝑖+1}⋯𝑤_{𝑖+𝐶} wC=wi−C⋯wi−1wi+1⋯wi+C作为输入，计算句子和上下文词语的平均词向量（或采用向量拼接的方式）,即左右开窗为C，用两边的句子来预测中间的这个句子。

PV-DBOW模型

对Skip-gram模型的扩展，形成了句子表示模型PV-DBOW（Distributed Bag-of-Words version of Paragraph Vector）。该模型以句子为输入，以句子中随机抽样的词语为输出，即要求句子能够预测句中的任意词语。其目标函数设计和训练方式与Skip-gram模型相同

Skip-Thought模型

Skip-Thought句子表示方法类似于PV-DBOW模型，不同于PV-DBOW模型利用句子预测句中的词语，Skip-Thought模型利用当前句子 𝑠 𝑘 𝑠_𝑘 sk预测前一个句子 𝑠 𝑘 − 1 𝑠_{𝑘−1} sk−1与后一个句子 𝑠 𝑘 + 1 𝑠_{𝑘+1} sk+1。该模型认为，文本中连续出现的句子 𝑠 𝑘 − 1 𝑠 𝑘 𝑠 𝑘 + 1 𝑠_{𝑘−1}𝑠_𝑘𝑠_{𝑘+1} sk−1sksk+1表达的意思比较接近，因此，根据句子 𝑠 𝑘 𝑠_𝑘 sk的语义，可以重构出前后两个句子。

CNN模型

对于一个句子，卷积神经网络CNN以每个词的词向量为输入，通过顺序地对上下文窗口进行卷积（Convolution）总结局部信息，并利用池化层（Pooling）提取全局的重要信息，再经过其他网络层（卷积池化层、Dropout层、线性层等），得到固定维度的句子向量表达，以刻画句子全局性的语义信息。

整个过程可以概括为：

1. 词嵌入: 将词转化为固定维度的向量。
2. 卷积: 使用不同尺寸的卷积核在词向量序列上滑动，提取局部语义特征。
3. 池化: 对每个卷积核得到的特征图进行最大池化，捕获最重要的局部特征。
4. 拼接: 将所有卷积核的池化结果拼接起来，形成最终的固定长度的句子向量表示。

文档的表示学习

词袋方法

假设文档由𝑛个词语构成，视文档为词袋，其表示为词语向量的平均或加权平均。

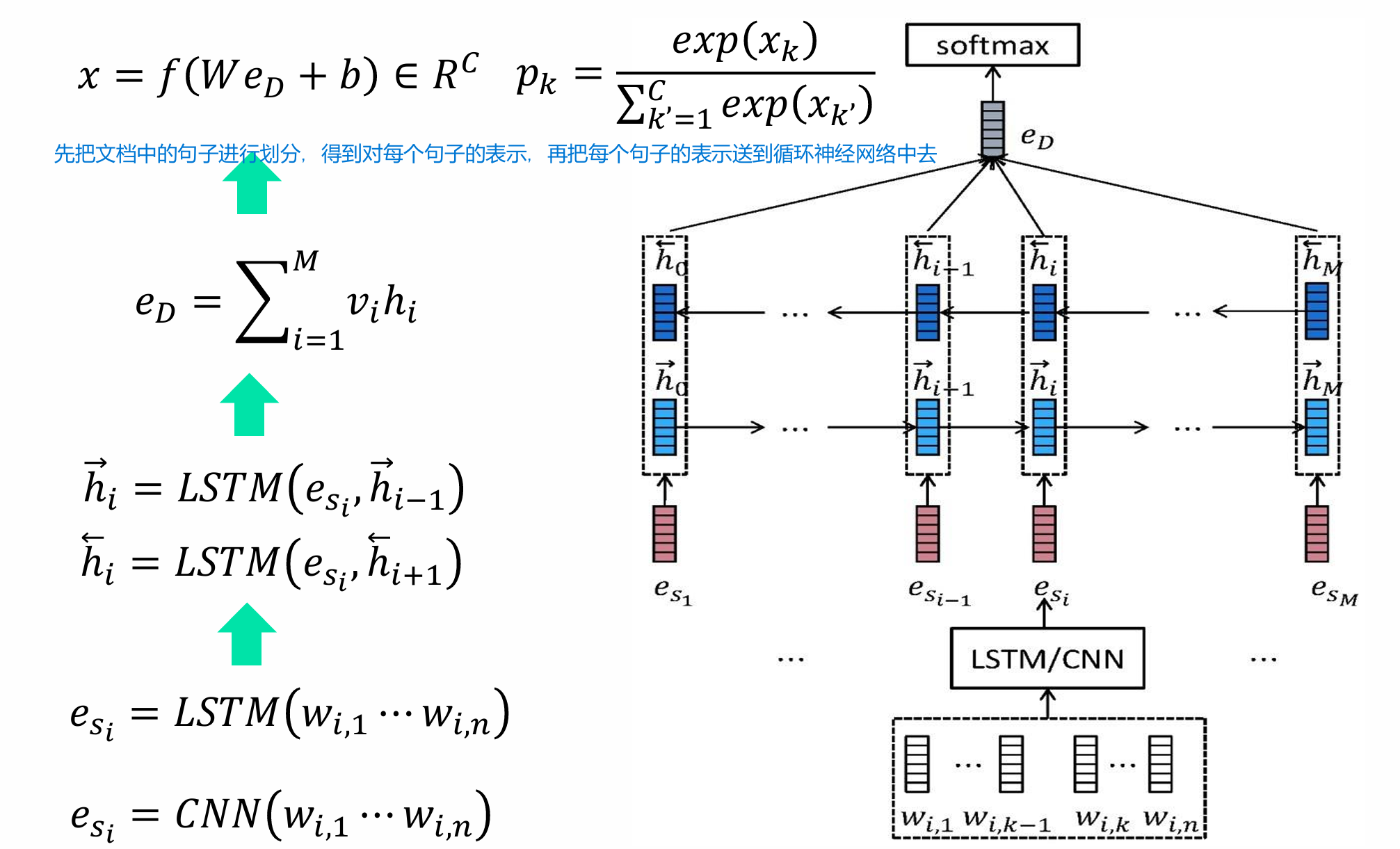
层次化模型

先把文档中的句子进行划分，得到对每个句子的表示，再把每个句子的表示送到循环神经网络中去进行下一步的计算。