本文从Python开发者视角解析「积分图像」技术------1984年由Frank Crow提出的预处理方法,通过一次遍历生成积分图,即可用常量时间计算任意矩形区域的像素和,彻底解决图像处理中反复计算区域和的性能痛点。我们用直观例子讲清原理,再通过Python代码演示落地,帮你理解它在模糊、检测等任务中的加速魔法。
一、为什么需要积分图像?
在计算机视觉中,计算图像区域和是高频操作:
- 均值模糊要算每个像素邻域的平均;
- 人脸检测要算Haar特征的矩形区域差;
- 边缘提取要算局部梯度的区域统计。
如果直接遍历每个区域计算,时间复杂度是O(H×W×K)(H/W为图像宽高,K为区域数量)------对于1080P图像和百万次查询,这会慢到无法接受。
积分图像的核心价值在于:用一次O(H×W)的预处理,换后续无限次O(1)的区域和查询。不管区域多大,查一次就出结果。
二、积分图像是什么?
积分图像是原始图像的预处理结果,定义为:
对于原始图像的每个位置
(x,y),积分图像对应位置的值是原始图像左上角到(x,y)的所有像素的和。
为了统一边界计算,我们会对原始图像做边界扩展 :在左边加一列全0,上边加一行全0,形成扩展图像ext_Raw。积分图像Int与ext_Raw大小相同,每个像素Int[x][y]代表ext_Raw中从(0,0)到(x,y)的区域和(坐标从0开始)。
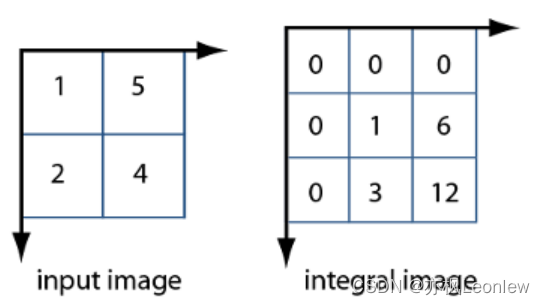
举个直观例子
假设原始图像是2×2的数组(坐标从1开始):Raw=[1524]Raw = \begin{bmatrix} 1 & 5 \\ 2 & 4 \end{bmatrix}Raw=[1254]
扩展后的ext_Raw是3×3(第一行/列全0):ext_Raw=[000015024]ext\_Raw = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 5 \\ 0 & 2 & 4 \end{bmatrix}ext_Raw= 000012054
对应的积分图像Int为:Int=[0000160312]Int = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 6 \\ 0 & 3 & 12 \end{bmatrix}Int= 0000130612
其中:
Int[1][1] = 1(原始图像(1,1)的和);Int[1][2] = 1+5=6(原始图像(1,1)到(1,2)的和);Int[2][2] = 1+5+2+4=12(整个原始图像的和)。
三、积分图像的生成:递推公式与Python实现
生成积分图像的关键是逐点递推 ,核心公式为:Int[x][y]=ext_Raw[x][y]+Int[x−1][y]+Int[x][y−1]−Int[x−1][y−1]Int[x][y] = ext\_Raw[x][y] + Int[x-1][y] + Int[x][y-1] - Int[x-1][y-1]Int[x][y]=ext_Raw[x][y]+Int[x−1][y]+Int[x][y−1]−Int[x−1][y−1]
公式解读:
ext_Raw[x][y]:当前位置的原始像素值;Int[x-1][y]:当前位置正上方所有像素的累积和;Int[x][y-1]:当前位置正左方所有像素的累积和;- Int[x-1][y-1]:前两步重复计算了左上角区域,需减去重叠部分。
Python代码实现生成逻辑
我们用numpy实现积分图像的生成(兼顾效率与可读性):
python
import numpy as np
def generate_integral_image(raw_image):
"""生成扩展后的积分图像"""
H, W = raw_image.shape
# 扩展边界:第一行/列全0
ext_raw = np.zeros((H + 1, W + 1), dtype=np.int32)
ext_raw[1:H+1, 1:W+1] = raw_image
integral = np.zeros_like(ext_raw)
# 逐行递推:先算行内前缀和,再加上方行的积分值
for x in range(1, H+1):
row_sum = 0 # 行内累加和
for y in range(1, W+1):
row_sum += ext_raw[x][y]
integral[x][y] = integral[x-1][y] + row_sum
return integral
# 测试:生成2×2原始图像的积分图
raw = np.array([[1, 5], [2, 4]])
integral = generate_integral_image(raw)
print("积分图像:")
print(integral)输出结果与之前的例子完全一致:
积分图像:
[[ 0 0 0]
[ 0 1 6]
[ 0 3 12]]四、如何用积分图像计算任意区域和?
积分图像的终极目标是快速计算任意矩形区域的和 。假设我们要算原始图像中左上角(a,b)、右下角(c,d)的矩形区域和(原始坐标从1开始),只需用积分图像的四个角点值组合:
区域和=Int[c+1][d+1]−Int[a][b]−Int[c+1][b]+Int[a][d+1]区域和 = Int[c+1][d+1] - Int[a][b] - Int[c+1][b] + Int[a][d+1]区域和=Int[c+1][d+1]−Int[a][b]−Int[c+1][b]+Int[a][d+1]
公式的几何意义
参考【在此处插入蓝色区域的几何示意图】,公式逻辑为:
Int[c+1][d+1]:整个大区域(原始图像到(c,d))的和;- 减去
Int[a][b]:去掉大区域上方的无关区域; - 减去
Int[c+1][b]:去掉大区域左方的无关区域; - 加上
Int[a][d+1]:补回重复减去的左上角重叠区域。
举个例子:计算单个像素值
如果要算原始图像中(2,2)点的像素值(区域是(2,2)到(2,2)),代入公式得:像素值=Int[3][3]−Int[2][2]−Int[3][2]+Int[2][3]=12−3−6+1=4像素值 = Int[3][3] - Int[2][2] - Int[3][2] + Int[2][3] = 12 - 3 - 6 + 1 = 4像素值=Int[3][3]−Int[2][2]−Int[3][2]+Int[2][3]=12−3−6+1=4
结果与原始图像一致!
五、Python实战:计算任意区域和
我们扩展代码,实现区域和的计算:
python
def get_region_sum(integral, a, b, c, d):
"""计算原始图像中矩形区域的和"""
# 转换为积分图像的坐标(扩展后的)
x1, y1 = a, b
x2, y2 = c + 1, d + 1
return integral[x2][y2] - integral[x1][y1] - integral[x2][y1] + integral[x1][y2]
# 测试:计算区域(1,2)-(2,2)的和(5+4=9)
region_sum = get_region_sum(integral, 1, 2, 2, 2)
print("区域(1,2)-(2,2)的和:", region_sum) # 输出9六、积分图像的应用场景
积分图像的核心优势是空间换时间,典型应用包括:
- 均值滤波/高斯模糊:快速计算每个像素邻域的平均;
- Haar特征检测:Viola-Jones人脸检测器的核心组件,用积分图快速计算矩形特征差;
- 边缘检测:如Sobel算子的梯度计算,需统计局部区域的像素变化;
- 对象检测:行人、车辆等目标的特征提取,需大量区域和计算。
总结
积分图像是计算机视觉中的"预处理神器"------用一次遍历生成积分图,就能把后续的区域和计算从"慢遍历"变成"秒查询"。本文用Python代码和直观例子讲清了它的原理:
- 边界扩展:统一计算逻辑;
- 递推公式:生成积分图像的核心;
- 区域和计算:四个角点的组合魔法。
如果你在做图像处理时遇到"反复计算区域和"的瓶颈,不妨试试积分图像------它可能会给你的代码带来数量级的速度提升!
获取更多资料
欢迎下载学习资料,包含:机器学习,深度学习,大模型,CV方向,NLP方向,kaggle大赛,实战项目、自动驾驶等。
"点击" 免费获取 。