迷宫寻路是回溯算法的经典应用场景,其核心是在复杂路径中通过 "尝试 - 回溯" 探索所有可能的路径,最终找到通往终点的解。无论是在算法竞赛(如 LeetCode)还是考研计算机专业基础综合(408)中,迷宫寻路问题及其变种都是考察回溯思想的高频考点。
迷宫寻路的回溯算法思路
问题定义
迷宫通常被抽象为一个二维网格,其中:
- 0 表示可通行的空地。
- 1 表示不可通行的墙壁。
- 起点 (startX, startY) 和终点 (endX, endY) 是网格中的两个特殊位置。
问题目标:从起点出发,通过上下左右四个方向移动,找到一条到达终点的路径(或所有路径),移动过程中不能穿过墙壁,也不能重复经过同一位置。
回溯算法核心思路
回溯算法通过递归探索所有可能的路径,若当前路径无法到达终点,则回溯到上一步,尝试其他方向。具体步骤如下:
- 标记当前位置:到达某位置 (x, y) 后,标记该位置为 "已访问"(避免重复进入)。
- 判断终点:若 (x, y) 是终点,则记录当前路径(若需所有路径)或直接返回成功。
- 尝试方向:依次尝试上、下、左、右四个方向:
- 若方向未越界、不是墙壁、未被访问,则递归探索该方向。
- 若递归返回成功(找到终点),则继续回溯或返回;若失败,则尝试下一个方向。
- 回溯清理:若所有方向均无法到达终点,取消当前位置的 "已访问" 标记,返回上一步。
算法流程图示
(以 3×3 迷宫为例)
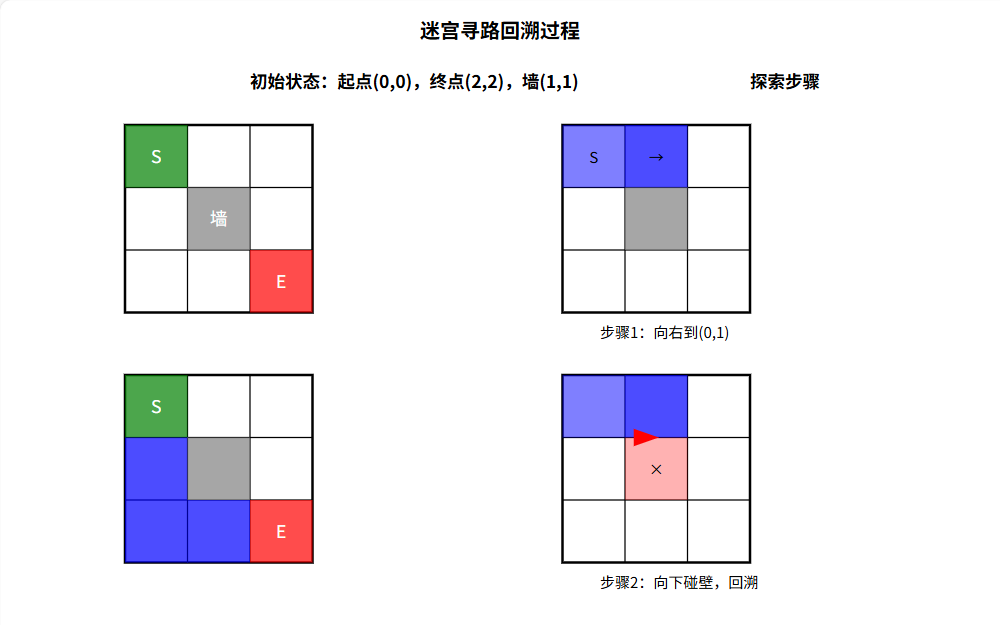
LeetCode例题实战
例题1:490. 迷宫(中等)
题目描述
:由空地(0)和墙(1)组成的迷宫中有一个球。球可以向上下左右四个方向滚动,但在遇到墙之前不会停止滚动。当球停下时,可以选择下一个方向。给定球的起始位置、目的地和迷宫,判断球能否在目的地停下。
示例:
输入:
迷宫:[[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]]
起始位置:[0,4]
目的地:[4,4]
输出:true
解释:球可以滚动到目的地(路径:右→下→左→下→右)
解题思路
1. **与传统迷宫的区别**:球会"滚动"直到撞墙才停下,而非一步一格移动。
2. **回溯思路**:
- 从起点出发,尝试四个方向滚动,记录停下的位置(撞墙前的最后一个空地)。
- 若停下的位置是终点,返回true。
- 若该位置已访问过,跳过(避免循环)。
- 否则标记为已访问,递归探索从该位置出发的四个方向。
- 回溯时无需取消标记(因滚动路径唯一,不会重复访问)。
代码实现
java
class Solution {
private int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 上、下、左、右
private int rows, cols;
private boolean[][] visited;
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
rows = maze.length;
cols = maze[0].length;
visited = new boolean[rows][cols];
return backtrack(maze, start[0], start[1], destination);
}
private boolean backtrack(int[][] maze, int x, int y, int[] dest) {
// 若当前位置是终点,返回true
if (x == dest[0] && y == dest[1]) {
return true;
}
// 标记当前位置为已访问
visited[x][y] = true;
// 尝试四个方向滚动
for (int[] dir : directions) {
int nx = x, ny = y;
// 滚动直到撞墙
while (nx + dir[0] >= 0 && nx + dir[0] < rows &&
ny + dir[1] >= 0 && ny + dir[1] < cols &&
maze[nx + dir[0]][ny + dir[1]] == 0) {
nx += dir[0];
ny += dir[1];
}
// 若停下的位置未访问,递归探索
if (!visited[nx][ny] && backtrack(maze, nx, ny, dest)) {
return true;
}
}
// 所有方向均无法到达,返回false
return false;
}
}复杂度分析
- 时间复杂度:O (rows×cols×(rows+cols)),每个位置最多访问一次,每次滚动最多移动 rows+cols 格。
- 空间复杂度:O (rows×cols),visited 数组和递归栈的空间。
例题 2:79. 单词搜索(中等)
题目描述:给定一个 m x n 二维网格和一个单词,找出该单词是否存在于网格中。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中 "相邻" 单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
解题思路
- 问题抽象:网格可视为特殊迷宫,每个单元格是 "字母",路径需按单词顺序,且不可重复访问。
- 回溯思路:
- 遍历网格,找到单词首字母作为起点。
- 从起点出发,尝试四个方向,若下一个字母匹配且未访问,递归探索。
- 若递归长度等于单词长度,返回 true。
- 回溯时取消当前单元格的访问标记。
代码实现
java
class Solution {
private int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private int rows, cols;
private boolean[][] visited;
public boolean exist(char[][] board, String word) {
rows = board.length;
cols = board[0].length;
visited = new boolean[rows][cols];
// 遍历网格找起点
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (board[i][j] == word.charAt(0) && backtrack(board, word, i, j, 0)) {
return true;
}
}
}
return false;
}
private boolean backtrack(char[][] board, String word, int x, int y, int index) {
// 若匹配到单词末尾,返回true
if (index == word.length() - 1) {
return true;
}
visited[x][y] = true;
// 尝试四个方向
for (int[] dir : directions) {
int nx = x + dir[0];
int ny = y + dir[1];
// 检查边界、未访问、字母匹配
if (nx >= 0 && nx < rows && ny >= 0 && ny < cols &&
!visited[nx][ny] && board[nx][ny] == word.charAt(index + 1)) {
if (backtrack(board, word, nx, ny, index + 1)) {
return true;
}
}
}
// 回溯:取消标记
visited[x][y] = false;
return false;
}
}复杂度分析
- 时间复杂度:O (m×n×3^L),m 和 n 为网格尺寸,L 为单词长度。每个单元格最多访问一次,每次有 3 个新方向(排除来时方向)。
- 空间复杂度:O (L),递归栈深度为 L(单词长度),visited 数组为 O (m×n)。
考研 408 例题解析
例题 1:概念辨析题(选择题)
题目:关于回溯算法求解迷宫寻路问题,下列说法正确的是( )。
A. 回溯算法总能找到最短路径
B. 回溯算法的时间复杂度一定优于广度优先搜索(BFS)
C. 回溯算法通过递归实现,无需显式栈
D. 回溯过程中必须恢复访问标记,否则可能遗漏有效路径
答案:D
解析:
- A 错误:回溯算法会探索所有路径,但不一定优先找到最短路径(BFS 更适合最短路径)。
- B 错误:回溯算法时间复杂度通常为指数级(如 O (4^(m×n))),而 BFS 为 O (m×n),更优。
- C 错误:回溯算法的递归本质是利用系统栈,仍属于栈结构,只是无需手动实现。
- D 正确:若不恢复访问标记,已探索路径的标记会阻塞其他可能的有效路径,导致漏解。
例题 2:算法设计题(408 高频考点)
题目:设计一个回溯算法,找出迷宫中从起点到终点的所有路径。要求每条路径用坐标序列表示(如(0,0)→(0,1)→...→(m-1,n-1)),并分析算法的时间复杂度。
解题思路
- 数据结构:
-
- maze:二维数组表示迷宫(0 为通路,1 为墙)。
-
- path:列表记录当前路径的坐标。
-
- visited:二维数组标记已访问的位置。
-
- result:列表存储所有有效路径。
- 递归函数:backtrack(x, y)表示从(x,y)出发探索路径。
- 步骤:
-
- 若(x,y)是终点,将当前path加入result。
-
- 否则,对四个方向:
-
-
- 若方向合法(不越界、非墙、未访问),标记访问,加入path,递归探索。
-
-
-
- 回溯:移除path中的坐标,取消访问标记。
-
代码实现
java
import java.util.*;
public class MazeAllPaths {
private int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private int rows, cols;
private List<List<String>> result = new ArrayList<>();
public List<List<String>> findAllPaths(int[][] maze, int[] start, int[] end) {
rows = maze.length;
cols = maze[0].length;
boolean[][] visited = new boolean[rows][cols];
List<String> path = new ArrayList<>();
// 起点合法性检查
if (maze[start[0]][start[1]] == 1) {
return result;
}
path.add("(" + start[0] + "," + start[1] + ")");
visited[start[0]][start[1]] = true;
backtrack(maze, start[0], start[1], end, visited, path);
return result;
}
private void backtrack(int[][] maze, int x, int y, int[] end,
boolean[][] visited, List<String> path) {
// 到达终点,记录路径
if (x == end[0] && y == end[1]) {
result.add(new ArrayList<>(path));
return;
}
// 尝试四个方向
for (int[] dir : directions) {
int nx = x + dir[0];
int ny = y + dir[1];
// 检查边界、是否为墙、是否已访问
if (nx >= 0 && nx < rows && ny >= 0 && ny < cols &&
maze[nx][ny] == 0 && !visited[nx][ny]) {
// 标记访问,加入路径
visited[nx][ny] = true;
path.add("(" + nx + "," + ny + ")");
// 递归探索
backtrack(maze, nx, ny, end, visited, path);
// 回溯:移除路径,取消标记
path.remove(path.size() - 1);
visited[nx][ny] = false;
}
}
}
}复杂度分析
- 时间复杂度:O (4^(m×n)),每个单元格最多被访问一次,每次有 4 个方向可选,最坏情况下需探索所有可能路径。
- 空间复杂度:O (m×n),包括visited数组(m×n)、递归栈深度(最坏为 m×n)和路径存储(最长路径长度为 m×n)。
迷宫寻路的扩展与应用
实际应用场景
- 机器人导航:机器人在未知环境中探索路径,类似迷宫寻路逻辑。
- 游戏开发:角色在地图中寻找宝藏、避开障碍物的路径规划。
- 网络路由:数据包在网络节点间的传输路径选择,需避开故障节点。
与其他算法的对比
|-------------|-------------|---------------|------------------|
| 算法 | 核心思路 | 适用场景 | 时间复杂度 |
| 回溯算法 | 递归探索所有路径 | 求所有路径、判断路径存在性 | O(4^(m×n)) |
| 广度优先搜索(BFS) | 队列逐层探索 | 求最短路径 | O(m×n) |
| 深度优先搜索(DFS) | 栈或递归深度探索 | 与回溯类似,实现方式不同 | O(4^(m×n)) |
| A * 算法 | 启发式搜索(估价函数) | 大规模迷宫的高效路径规划 | 接近 O (m×n)(最优情况) |
考研 408 备考要点
- 核心考点:回溯算法的递归实现、访问标记的管理、路径存储与恢复。
- 重点掌握:
- 迷宫寻路中 "边界检查""墙检查""访问检查" 三要素。
- 回溯与递归的关系,以及回溯过程中状态的恢复逻辑。
- 不同迷宫变种(如滚动球、带权值迷宫)的算法调整。
- 常见错误:
-
- 遗漏边界检查导致数组越界。
-
- 回溯时未恢复访问标记,导致路径探索不完整。
-
- 混淆 "一步一格" 与 "滚动到墙" 的移动逻辑。
总结
迷宫寻路问题是回溯算法的典型应用,其核心 "递归探索 - 标记 - 回溯" 逻辑可迁移到多种路径规划场景。本文通过 LeetCode 例题(490 题和 79 题)展示了不同约束条件下的回溯实现,通过考研 408 例题解析了概念辨析和全路径求解思路,并结合 SVG 图示直观呈现了探索与回溯的过程。
掌握迷宫寻路的关键在于:
- 明确问题约束(移动方式、路径规则),针对性设计探索逻辑。
- 严格管理访问标记,确保回溯时状态正确恢复。
- 理解回溯算法与其他路径算法的适用场景差异(如 BFS 更适合最短路径)。
在考研备考中,需重点关注回溯算法的时间复杂度分析和状态管理细节,这不仅有助于解决迷宫问题,也能深化对递归和组合优化问题的理解。
希望本文能够帮助读者更深入地理解贪心算法中迷宫寻路算法,并在实际项目中发挥其优势。谢谢阅读!
希望这份博客能够帮助到你。如果有其他需要修改或添加的地方,请随时告诉我。
