数据结构自学Day8: 堆的排序以及TopK问题

堆的概念

逻辑结构：完全二叉树（包括大根堆，小根堆）

物理结构：数组形式

大根堆：树中所有父亲大于等于孩子

小根堆：树中所有父亲小于等于孩子

作用：堆排序，返回前k个堆顶元素（TopK问题）

堆排序问题

由于我们的堆-->大根堆，小根堆都是以数组形式存储的，那么你可以通过数组的排序方法实现，例如冒泡排序，但是算法复杂度。

这里我们采用另外一种方式利用建立堆的方式来进行排序

利用小根堆-->降序排列，大根堆-->升序排列。

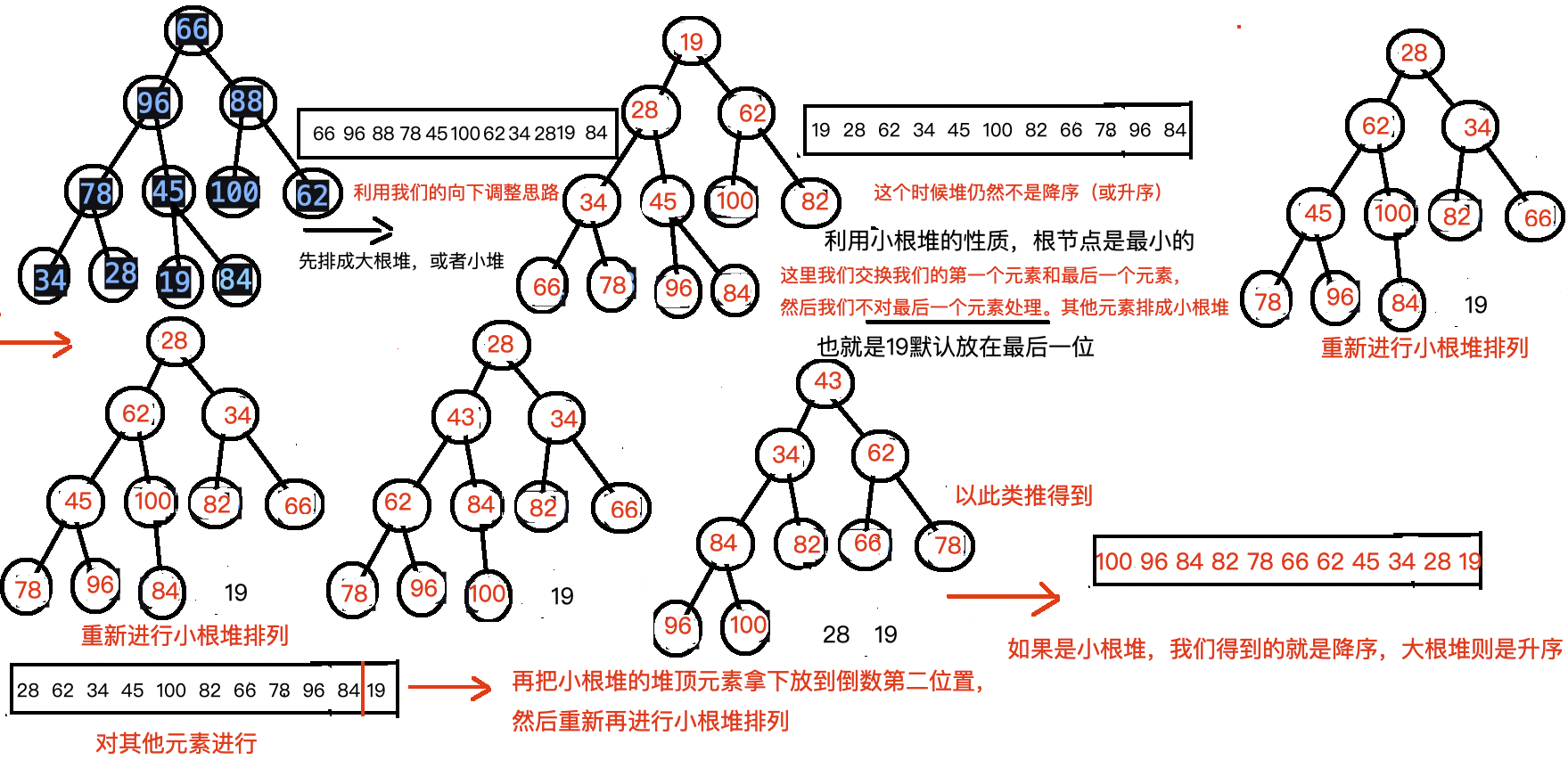
这里我们的算法的时间复杂度为。每次进行向下调整时的算法复杂度为

堆的实现我们在二叉树中实现了，这里我们只提供排序算法接口。

算法实现：

cpp 复制代码

void Heap_Sort(Heap* pheap){
    assert(pheap); 
    // 初始化之后已经是小根堆了
    // 降序排序 // 排降序建小堆，升序要建大堆。
    for (size_t end = pheap->size - 1; end > 0; end--) {
        Swap(&pheap->arr[0], &pheap->arr[end]);       // 最小值放末尾
        AdjustDown(pheap->arr, end, 0);               // 重新堆化（注意 end 是新长度）
    }
}

返回前k个堆顶元素（TopK问题）

面试题 17.14. 最小K个数

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

复制代码

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

提示：

0 <= len(arr) <= 100000
0 <= k <= min(100000, len(arr))

算法思路：

N个数中找出最大的或者最小的前k个：

1、先排序再提取--冒泡排序

2、大小根堆排序再提取 --

如果我们的N非常大呢？无法内存上排序。

3、建K个数的大根堆来解决 --> 先建k个数的大根堆，其他元素与堆顶元素比较大小，比堆顶小进入堆，然后重新再排成小根堆。

这里我们主要实现第三种思路：

新建一个k个元素的大根堆，将数组的元素与堆顶元素比较，小于堆顶元素就放入堆内，再进行堆处理。不断重复这一过程，最后这个堆留下的就是小的那k个元素

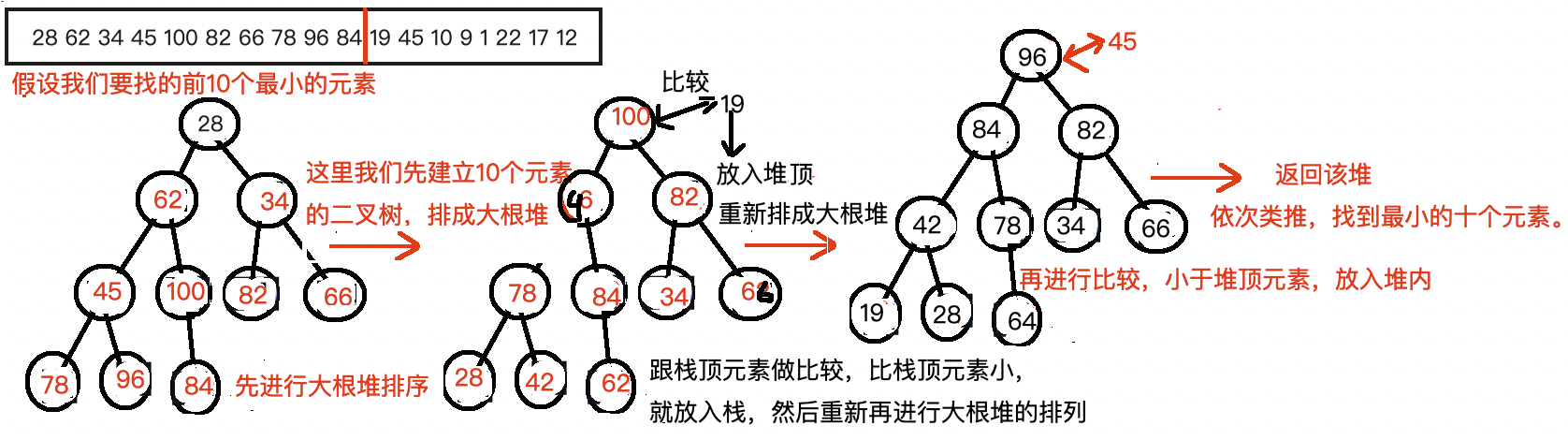
算法的实现：

cpp 复制代码

void Swap(int* p1,int* p2){
    assert(p1 && p2);
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

void AdjustDown(int* karr,int size, int root){
    assert(karr);
    int parent = root;
    int child = 2*parent+1;
    while(child<size){
        if(child+1<size && karr[child] < karr[child+1]){
            ++child;
        }
        if(karr[parent]<karr[child]){
            Swap(&karr[parent],&karr[child]);
            parent =child;
            child = 2*parent+1;
        }
        else{
            break;
        }
    }
}

int* smallestK(int* arr, int arrSize, int k, int* returnSize) {
    *returnSize = k;
    if(k == 0){
        return NULL;
    }
    int* karr = (int*) malloc(sizeof(int)*k);
    //初始化
    for(int i = 0;i<k;i++){
        karr[i] = arr[i];
    }
    //构建大根堆
    for(int root = (k-1-1)/2;root>=0;root--){
        AdjustDown(karr,k,root);
    }
    // 比较数组元素和堆顶元素
    for(int j = k;j<arrSize;j++){
        if(karr[0]>arr[j]){
            karr[0] = arr[j];
            AdjustDown(karr,k,0);
        }
    }
    return karr;
}

这里我们还是先利用到了上期内容我们实现的大根堆，小根堆的实现：二叉树的实现--堆，包括向下调整算法的应用，如何将一个数组元素排列成我们的堆。将数组中k个最小的数如何一步步存放到我们的堆的思想尤为重要，在面试题中常常出现！！

好了本期内容分享就到这结束了。谢谢大家的三连支持个