逻辑回归介绍
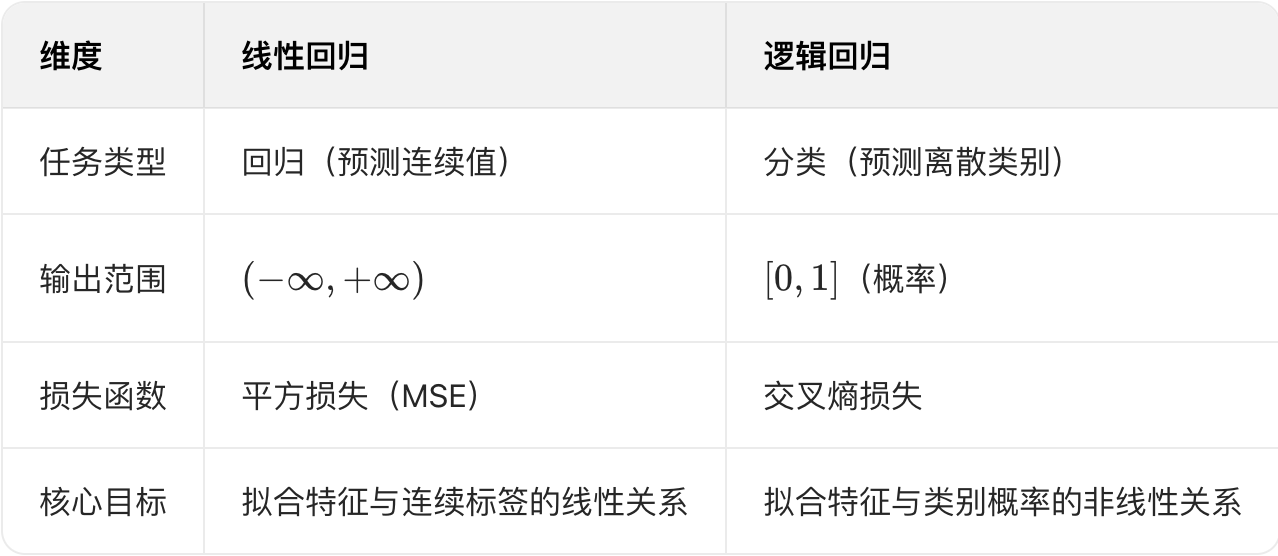
逻辑回归(Logistic Regression)是一种经典的分类算法,尽管名字中带有 "回归",但它本质上用于解决二分类问题(也可扩展到多分类)。
逻辑回归的本质是 "在线性回归的基础上,通过一个映射函数将输出转化为概率(从而实现对类别概率的预测)",这个映射函数就是Sigmoid函数。
逻辑回归是机器学习中最基础的分类算法之一,核心是通过 Sigmoid 函数将线性输出转化为概率,结合交叉熵损失和梯度下降求解参数。
它虽简单,但在实际业务中(尤其是需要可解释性的场景)仍被广泛使用,也是理解更复杂分类模型(如神经网络)的基础。
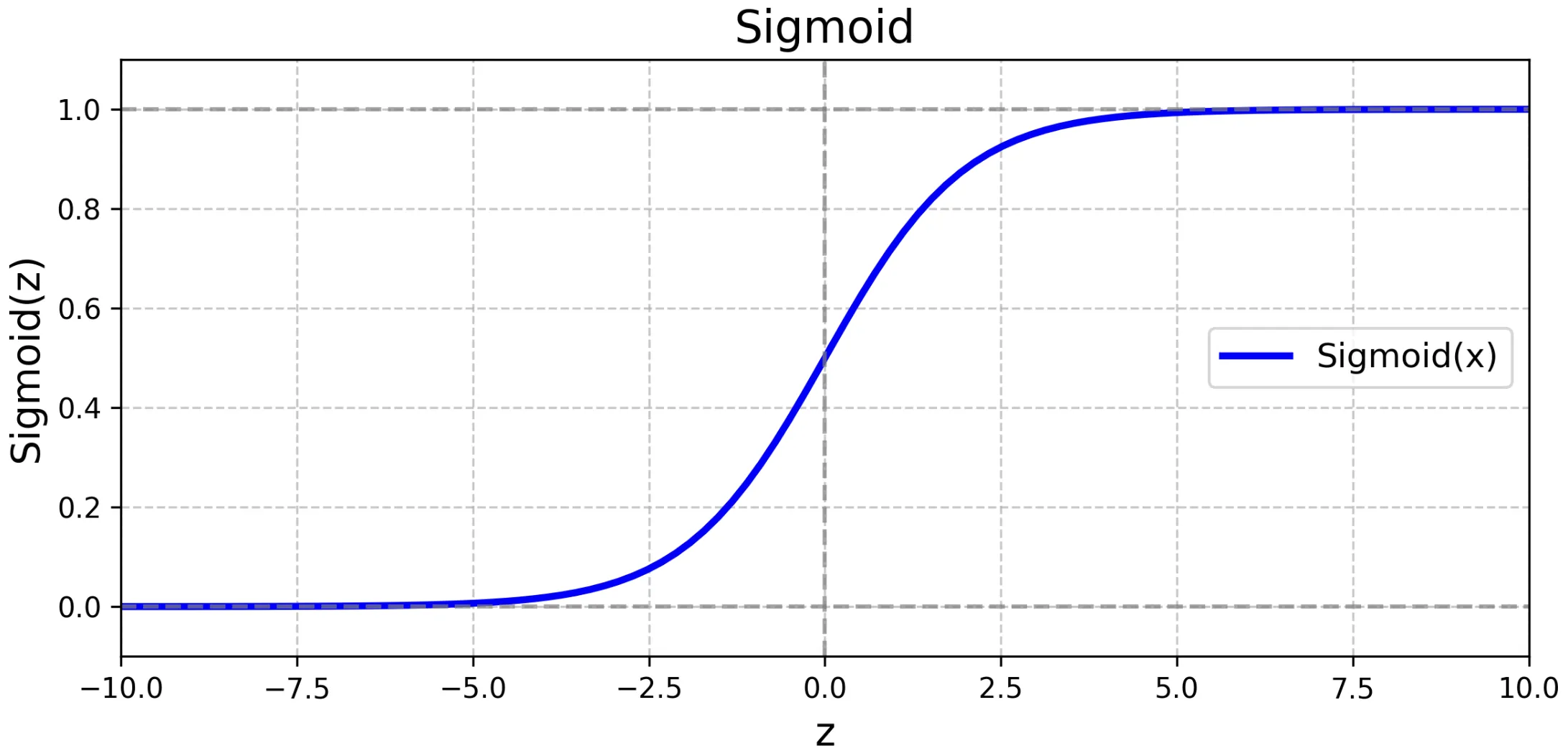
sigmoid函数
def sigmoid(z):
"""
Compute the sigmoid of z
Args:
z (ndarray): A scalar, numpy array of any size.
Returns:
g (ndarray): sigmoid(z), with the same shape as z
"""
g = 1 / (1 + np.exp(-z))
return g
逻辑回归模型
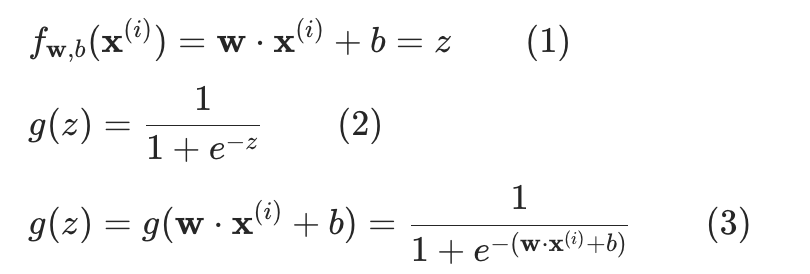
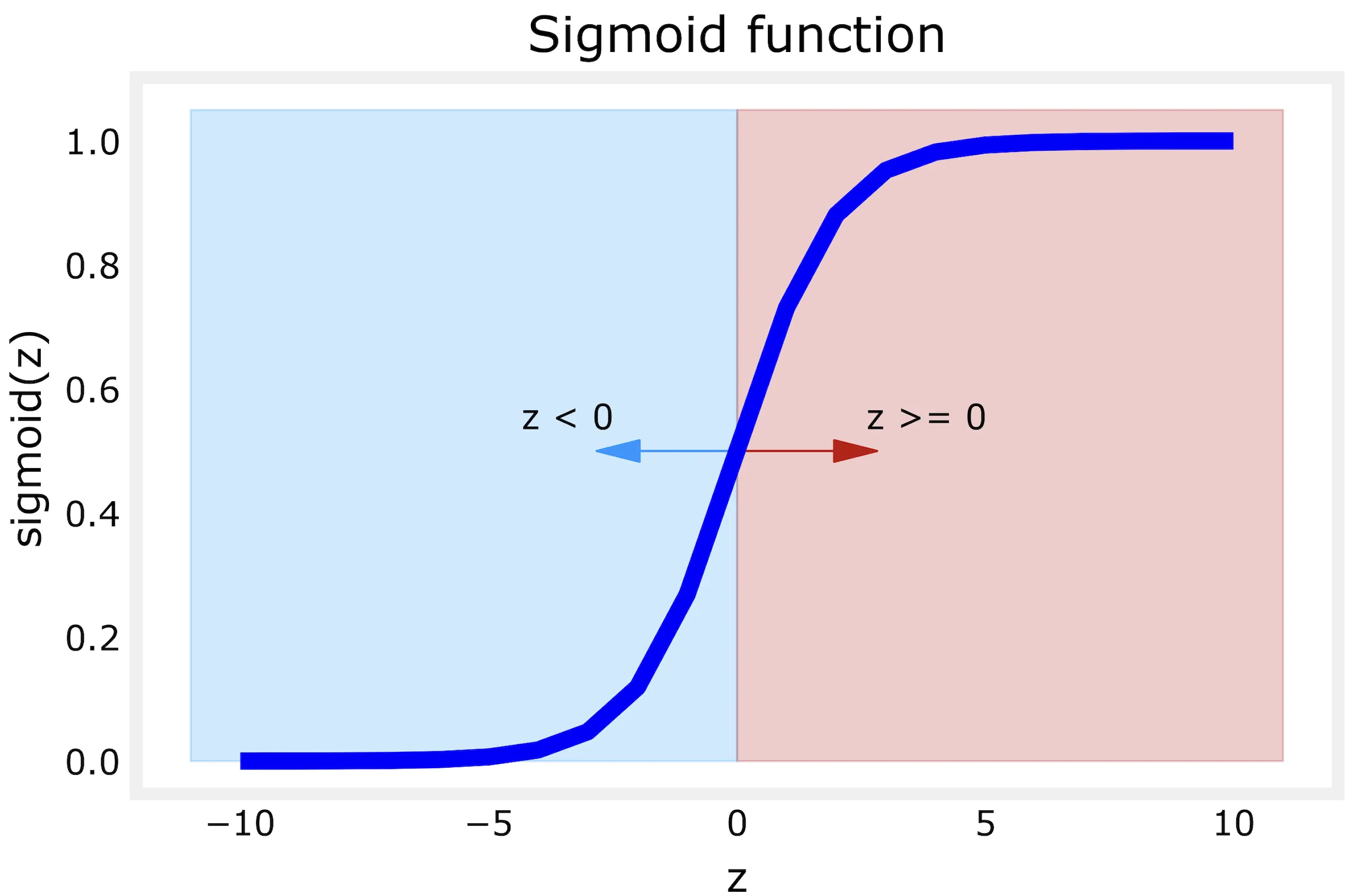
逻辑回归的决策边界
线性逻辑回归
根据sigmoid函数图象:z=0是中间位置,视为决策边界;那么为了得到决策边界的特征情况,我们假设:
- 线性模型 z = w1 * x1 + w2 * x2 + b
- 参数 w1=w2=1, b=03,那么x2 = -x1 + 3这条直线就是决策边界
如果特征x在这条线的右边,那么此逻辑回归则预测为1,反之则预测为0;(分为两类)

多项式逻辑回归
多项式回归决策边界,我们假设:
- 多项式模型:z = w1 * x12 + w2 * x22 + b
- 参数:w1=w2=1, b=-1
如果特征x在圆的外面,那么此逻辑回归则预测为1,反之则预测为0;(分为两类)

扩展:随着多项式的复杂度增加,还可以拟合更更多非线性的复杂情况
逻辑回归的损失函数
平方损失和交叉熵损失
回顾下线性回归的损失函数(平方损失):
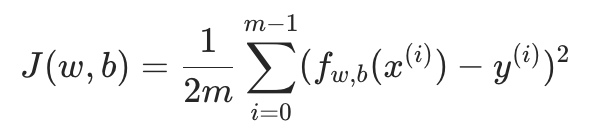
平方误差损失函数不适用于逻辑回归模型:平方损失在逻辑回归中是 "非凸函数"(存在多个局部最优解),难以优化;
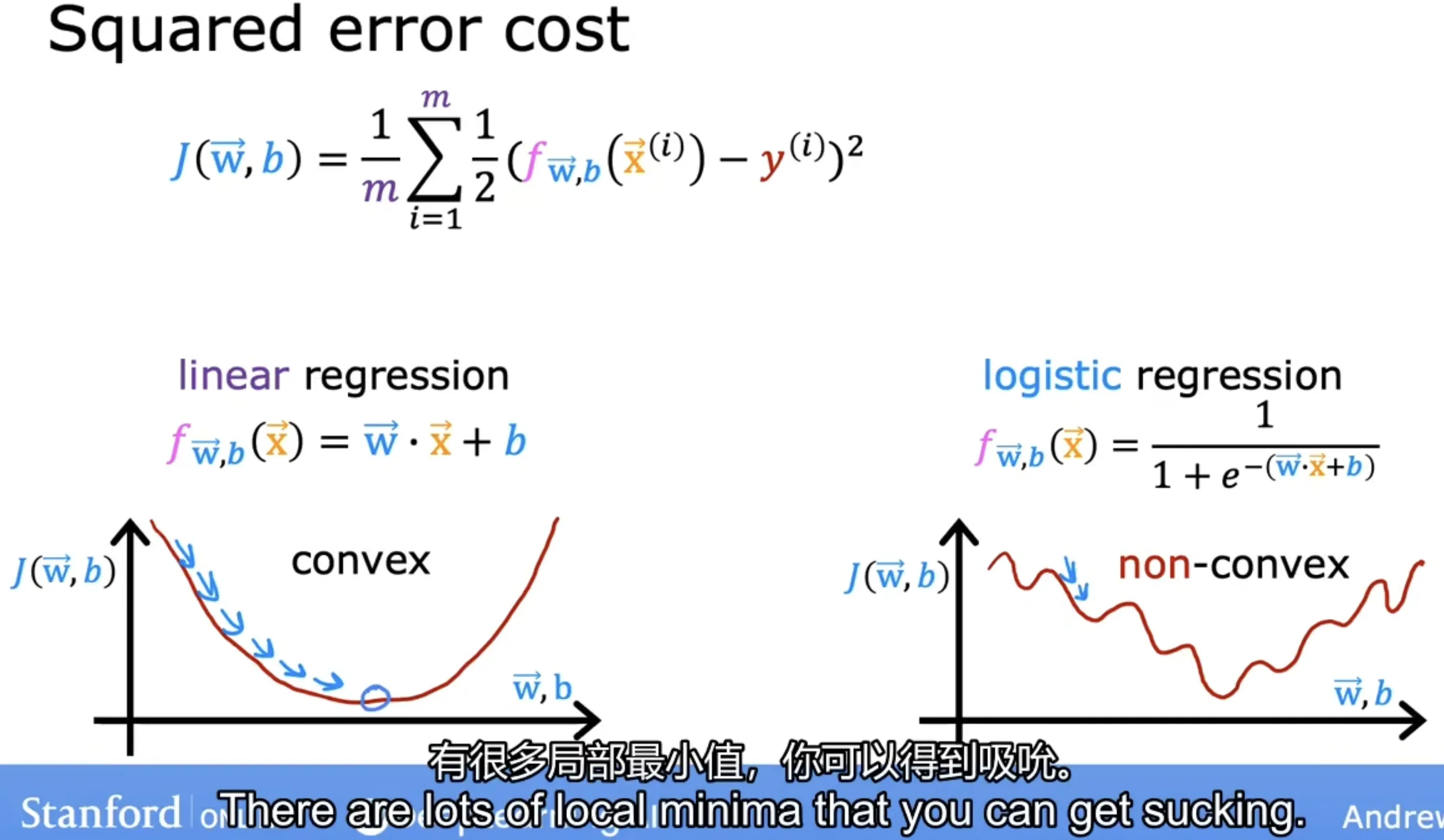
所以我们需要一个新的损失函数,即交叉熵损失;交叉熵损失是 "凸函数",可通过梯度下降高效找到全局最优。
交叉熵源于信息论,我们暂时不做深入介绍,直接给出交叉熵损失函数公式:

对数回顾
复习下对数函数的性质,以便理解为什么 交叉熵损失是 "凸函数"?
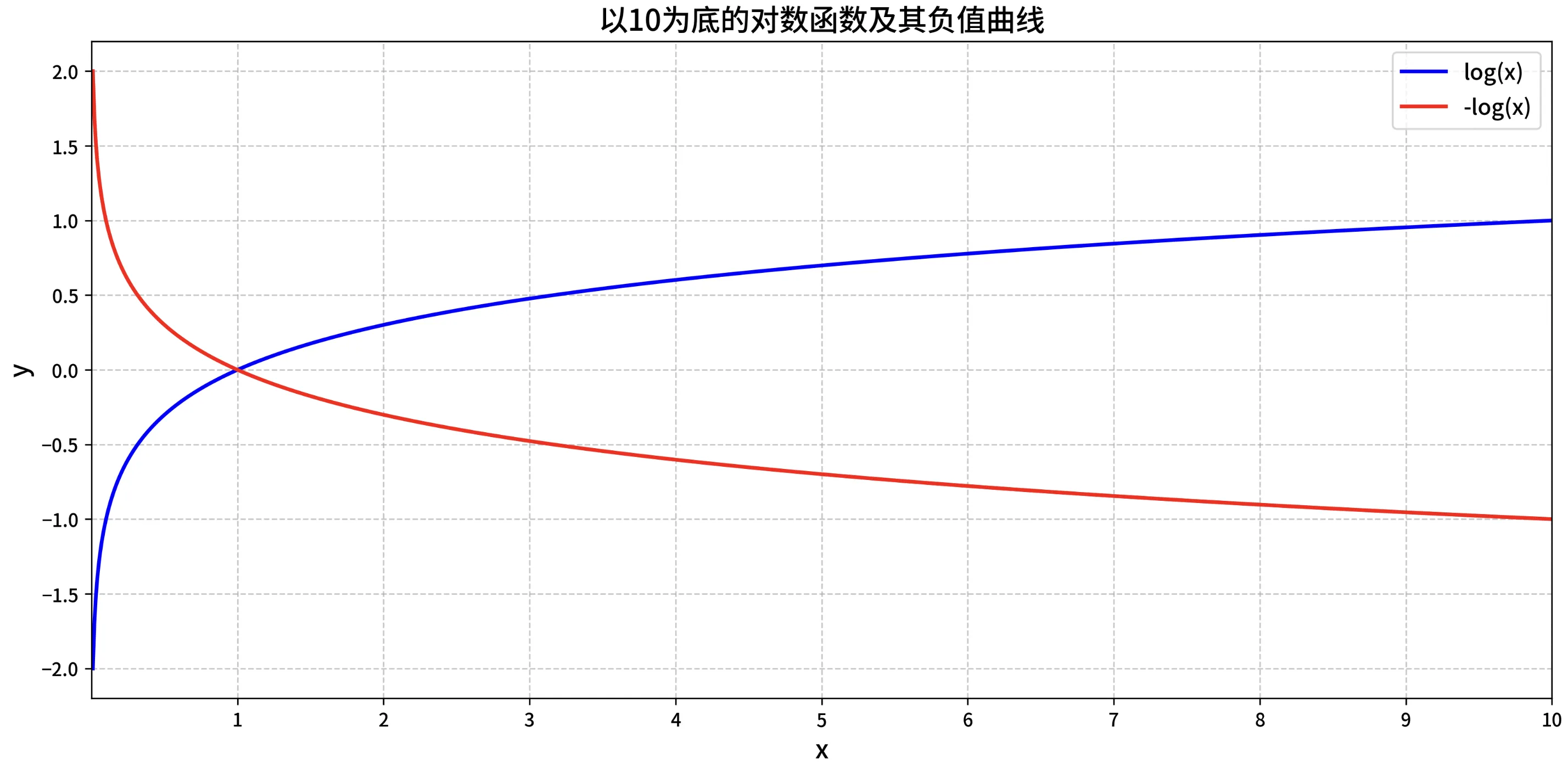
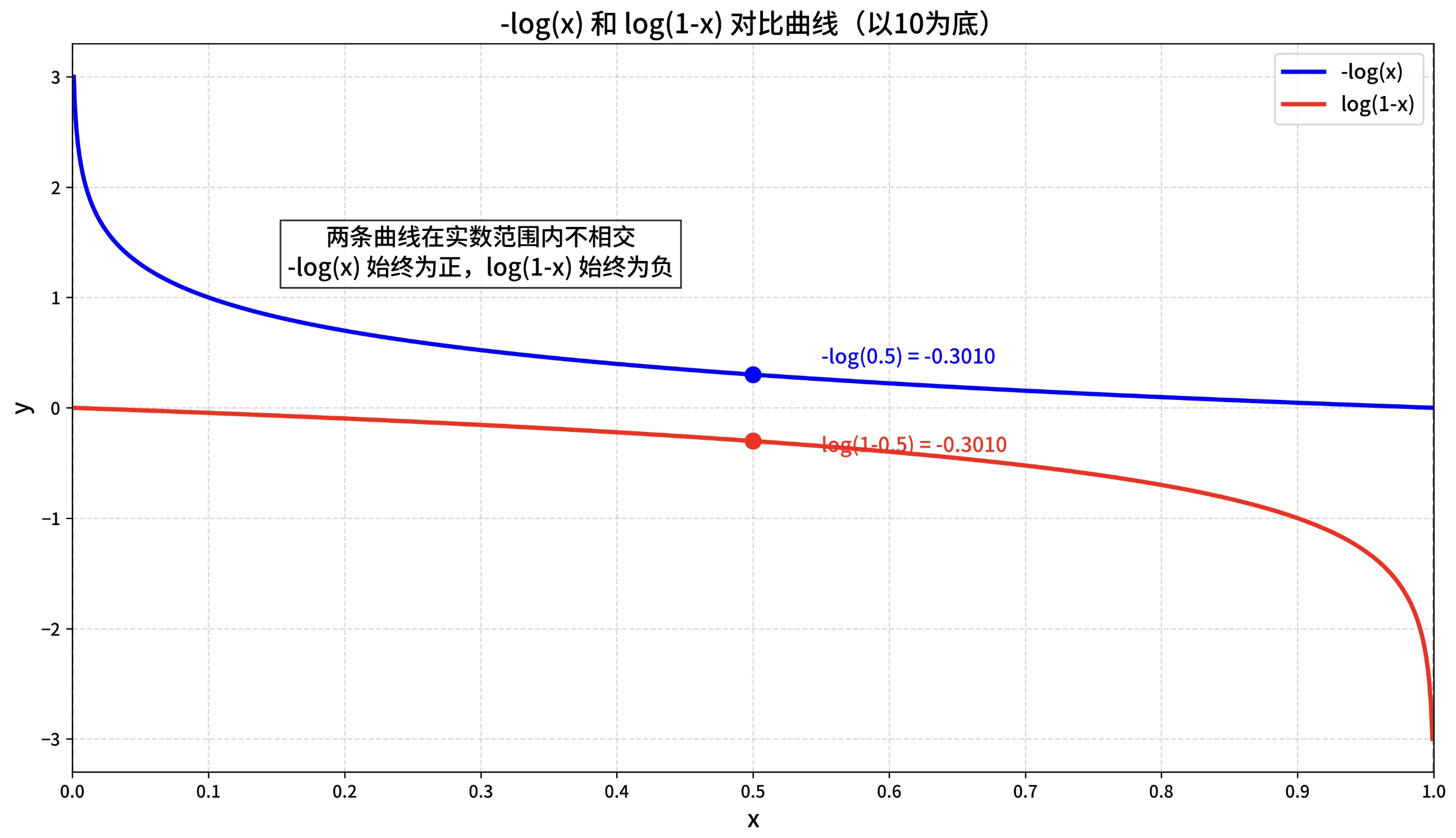
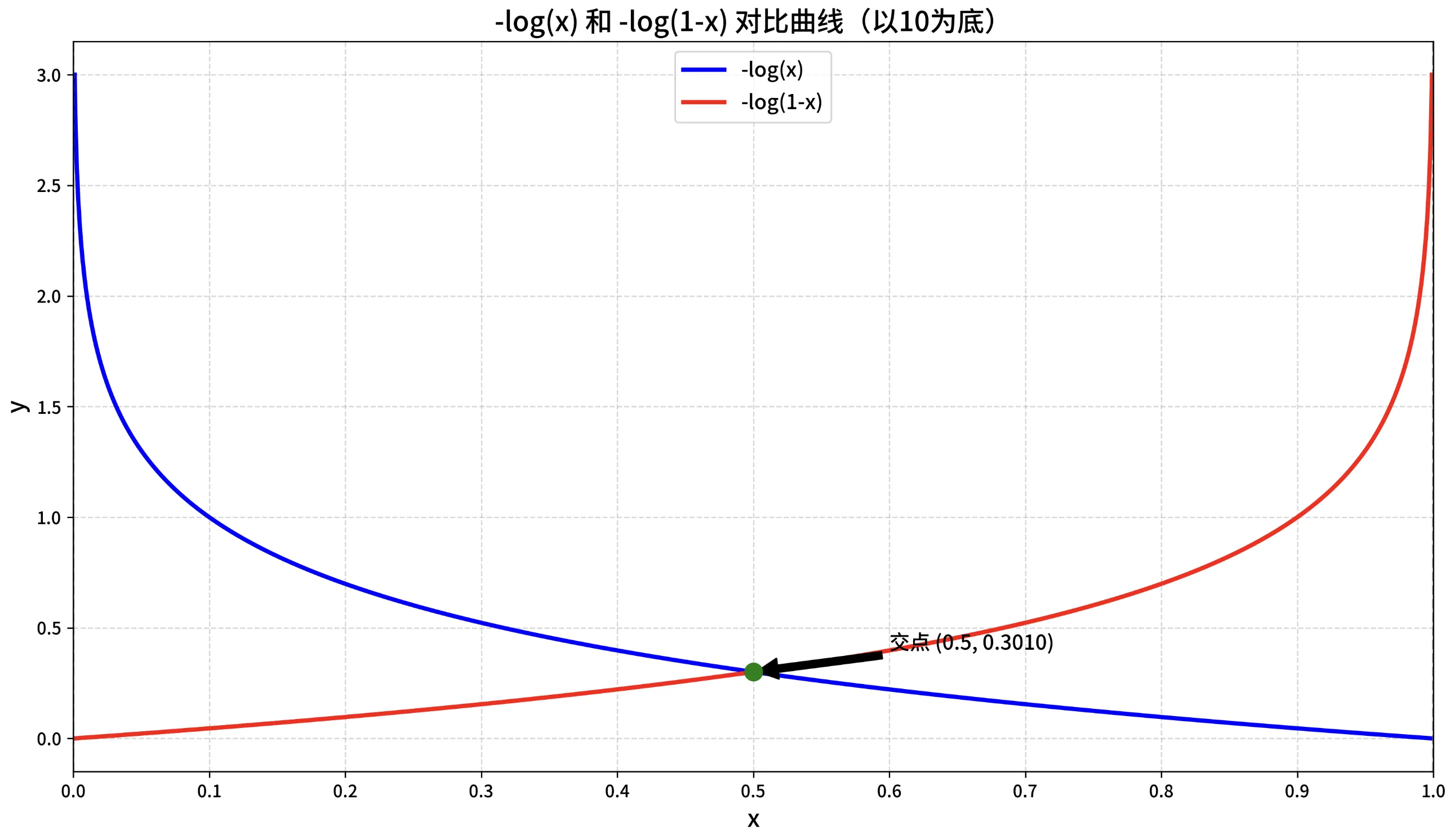
简化交叉熵损失函数
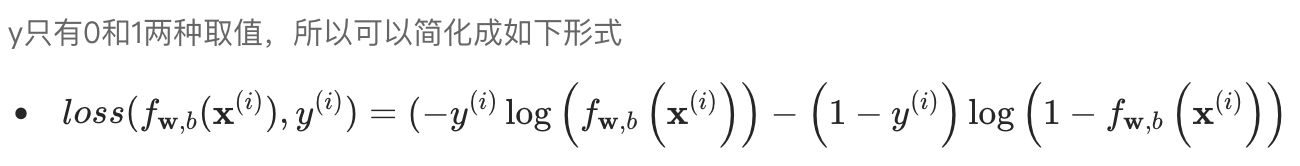
为什么要用这个函数来表示?来源自 最大释然估计(Maximum Likelihood),这里不做过多介绍。

简化结果:
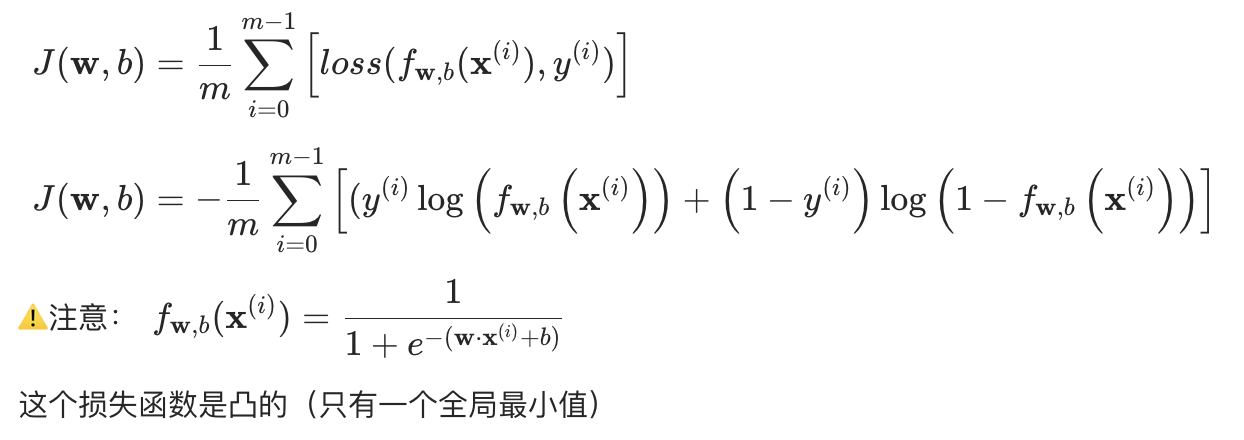
逻辑回归的梯度计算
自然对数求导公式:

链式求导法则:
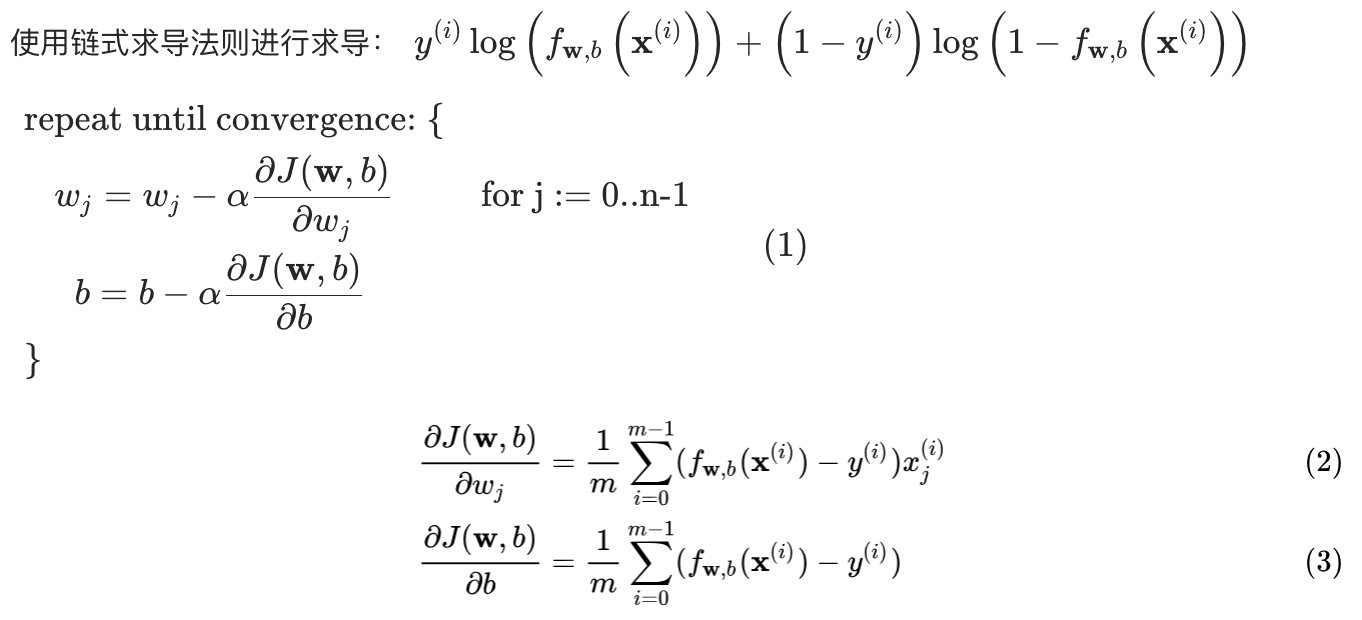
⚠️注意:

过拟合问题
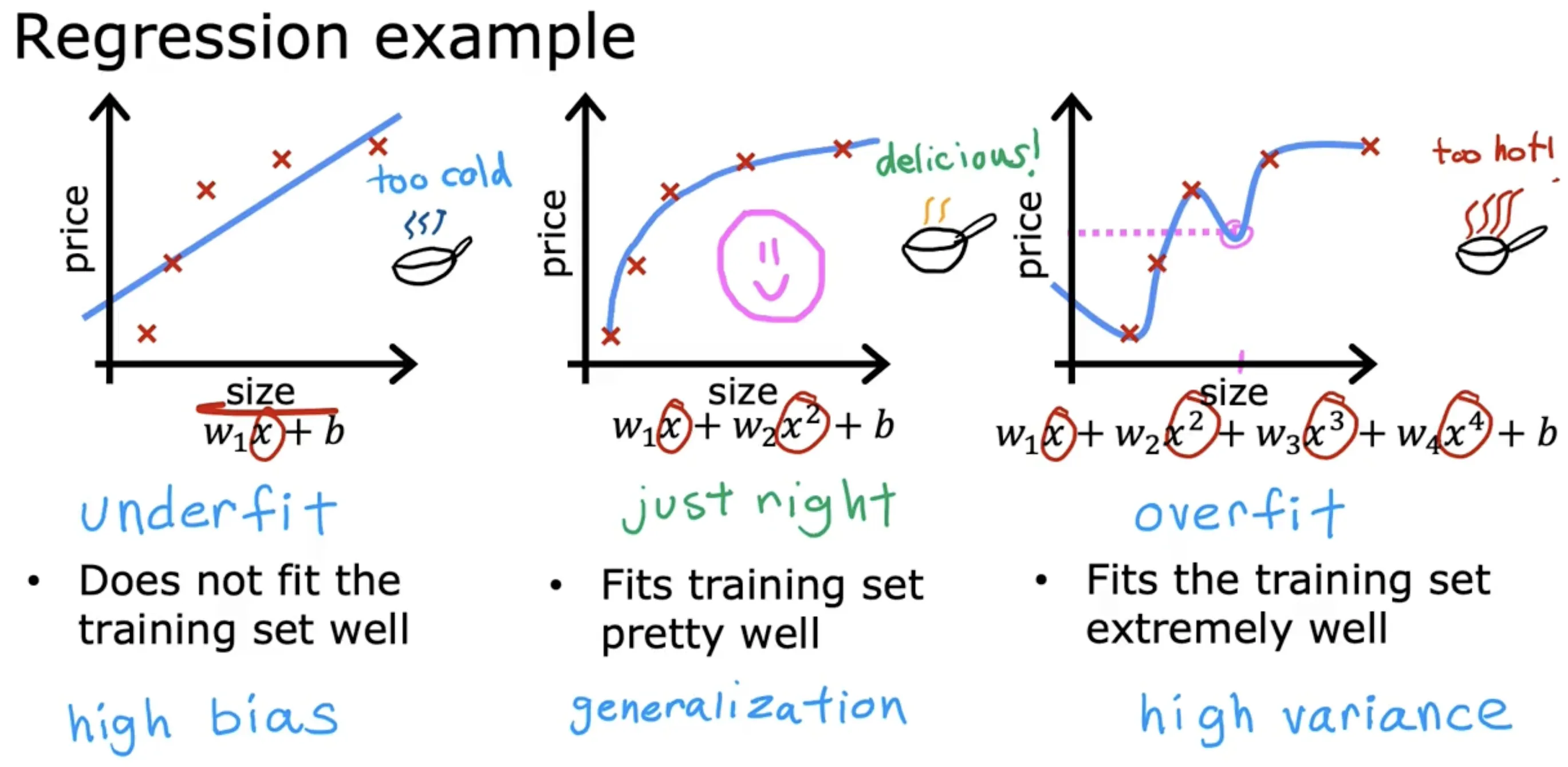
线性回归过拟合
逻辑回归过拟合
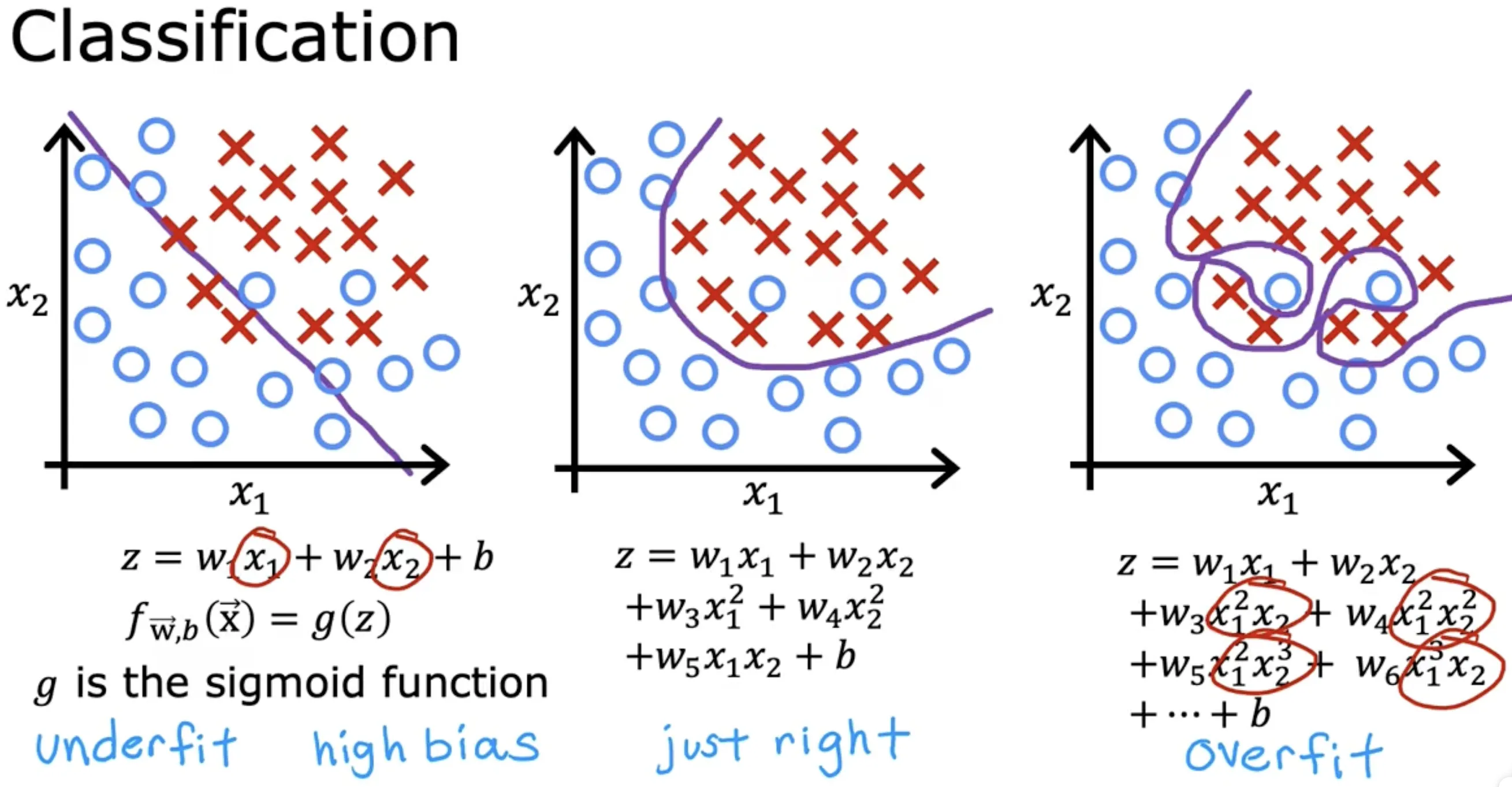
- 欠拟合(underfit),存在高偏差(bias)
- 泛化(generalization):希望我们的学习算法在训练集之外的数据上也能表现良好(预测准确)
- 过拟合(overfit),存在高方差(variance)
解决过拟合的办法
- 特征选择:只选择部分最相关的特征(基于直觉intuition)进行训练;缺点是丢掉了部分可能有用的信息
- 正则化:正则化是一种更温和的减少某些特征的影响,而无需做像测地消除它那样苛刻的事:
- 鼓励学习算法缩小参数,而不是直接将参数设置为0(保留所有特征的同时避免让部分特征产生过大的影响)
- 鼓励把 w1 ~ wn 变小,b不用变小
正则化模型
It turns out that regularization is a way
to more gently reduce ths impacts of some of the features without doing something as harsh as eliminating it outright.

关于正则化项的说明:

带正则化项的损失函数
正则化线性回归
损失函数:

梯度计算:

分析梯度计算公式,由于alpha和lambda通常是很小的值,所以相当于在每次迭代之前把参数w缩小了一点点,这也就是正则化的工作原理,如下所示:

正则化逻辑回归
损失函数:
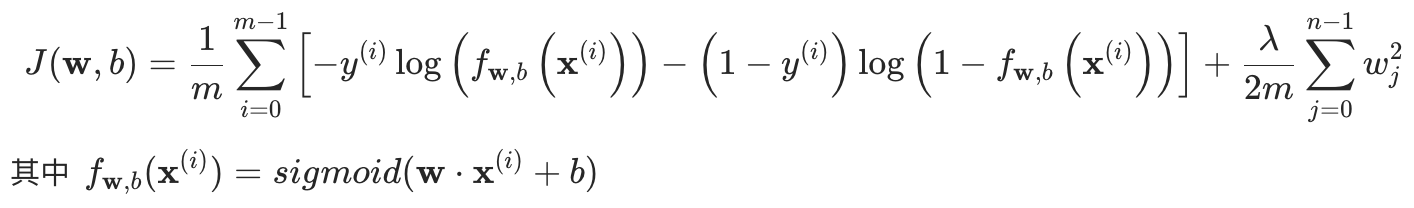
梯度计算:
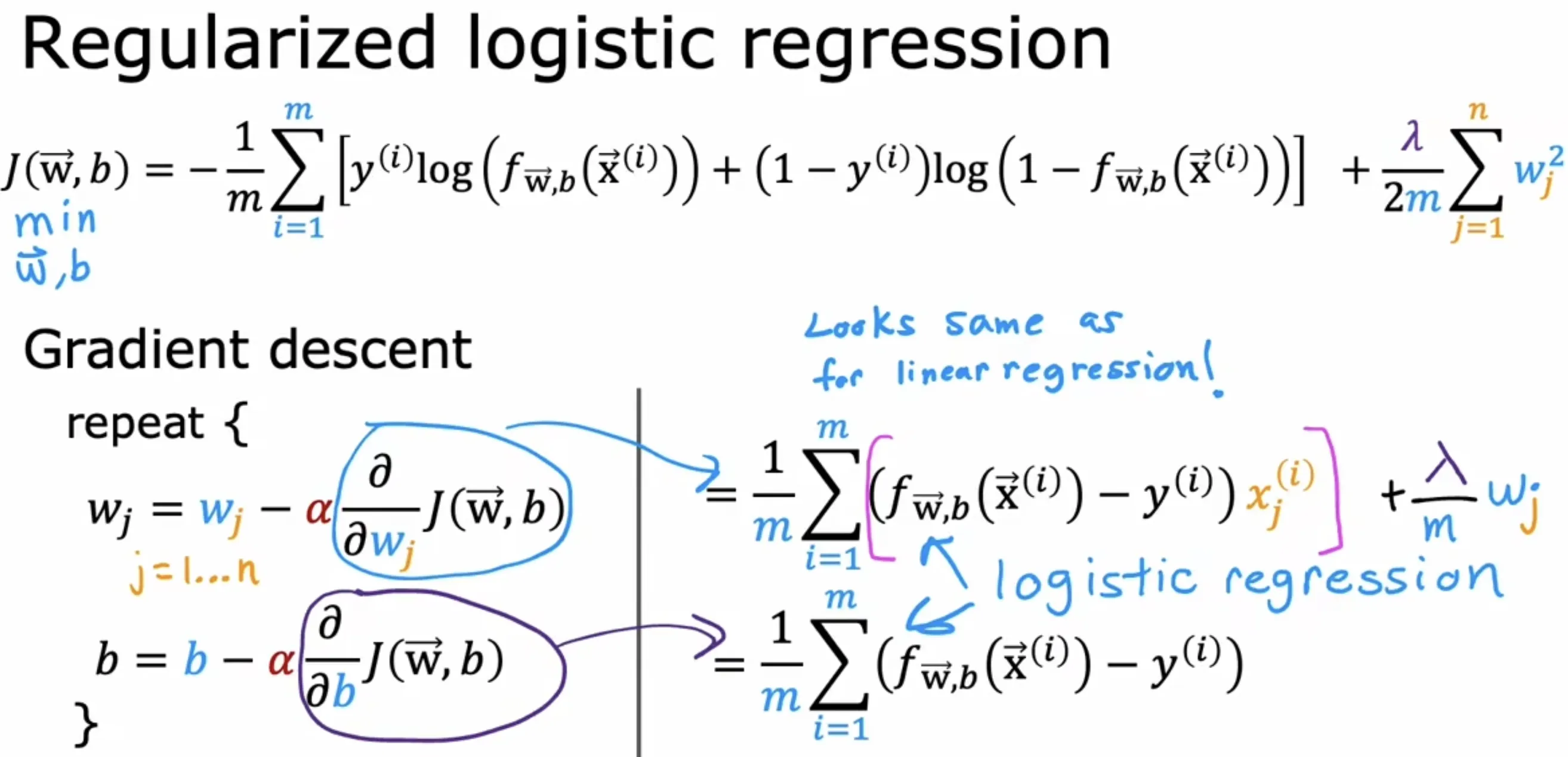
线性回归和逻辑回归正则化总结

逻辑回归实战
模型选择
可视化训练数据,基于此数据选择线性逻辑回归模型
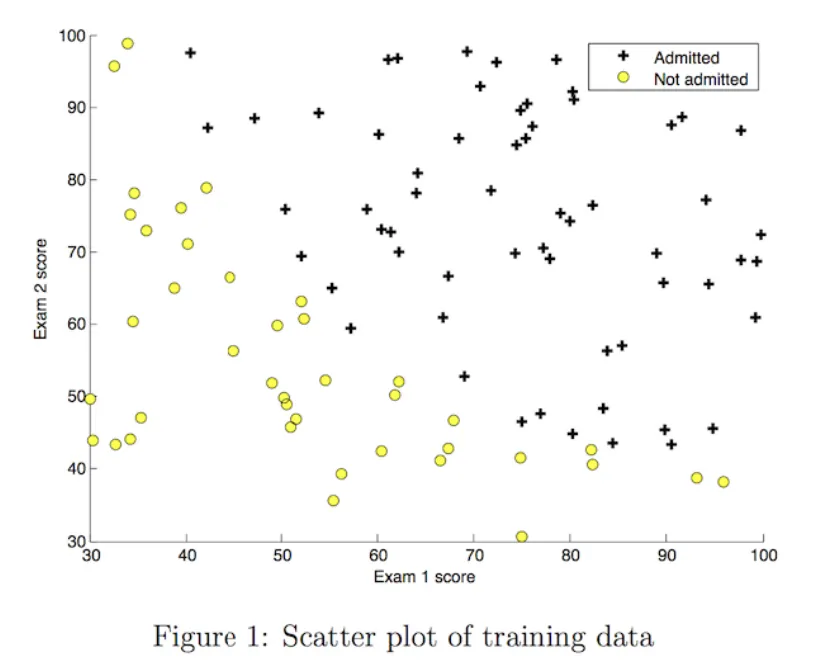
关键代码实现
def sigmoid(z):
g = 1 / (1 + np.exp(-z))
return g
def compute_cost(X, y, w, b, lambda_= 1):
"""
Computes the cost over all examples
Args:
X : (ndarray Shape (m,n)) data, m examples by n features
y : (array_like Shape (m,)) target value
w : (array_like Shape (n,)) Values of parameters of the model
b : scalar Values of bias parameter of the model
lambda_: unused placeholder
Returns:
total_cost: (scalar) cost
"""
m, n = X.shape
total_cost = 0
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i], w) + b)
loss = -y[i] * np.log(f_wb_i) - (1 - y[i]) * np.log(1 - f_wb_i)
total_cost += loss
total_cost = total_cost / m
return total_cost
def compute_gradient(X, y, w, b, lambda_=None):
"""
Computes the gradient for logistic regression
Args:
X : (ndarray Shape (m,n)) variable such as house size
y : (array_like Shape (m,1)) actual value
w : (array_like Shape (n,1)) values of parameters of the model
b : (scalar) value of parameter of the model
lambda_: unused placeholder.
Returns
dj_dw: (array_like Shape (n,1)) The gradient of the cost w.r.t. the parameters w.
dj_db: (scalar) The gradient of the cost w.r.t. the parameter b.
"""
m, n = X.shape
dj_dw = np.zeros(n)
dj_db = 0.
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i], w) + b)
diff = f_wb_i - y[i]
dj_db += diff
for j in range(n):
dj_dw[j] = dj_dw[j] + diff * X[i][j]
dj_db = dj_db / m
dj_dw = dj_dw / m
return dj_db, dj_dw
def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters, lambda_):
"""
Performs batch gradient descent to learn theta. Updates theta by taking
num_iters gradient steps with learning rate alpha
Args:
X : (array_like Shape (m, n)
y : (array_like Shape (m,))
w_in : (array_like Shape (n,)) Initial values of parameters of the model
b_in : (scalar) Initial value of parameter of the model
cost_function: function to compute cost
alpha : (float) Learning rate
num_iters : (int) number of iterations to run gradient descent
lambda_ (scalar, float) regularization constant
Returns:
w : (array_like Shape (n,)) Updated values of parameters of the model after
running gradient descent
b : (scalar) Updated value of parameter of the model after
running gradient descent
"""
# number of training examples
m = len(X)
# An array to store cost J and w's at each iteration primarily for graphing later
J_history = []
w_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
dj_db, dj_dw = gradient_function(X, y, w, b, lambda_)
w = w - alpha * dj_dw
b = b - alpha * dj_db
cost = cost_function(X, y, w, b, lambda_)
J_history.append(cost)
w_history.append(w)
if i % math.ceil(num_iters / 10) == 0:
print(f"{i:4d} cost: {cost:6f}, w: {w}, b: {b}")
return w, b, J_history, w_history #return w and J,w history for graphing
def predict(X, w, b):
m, n = X.shape
p = np.zeros(m)
for i in range(m):
f_wb = sigmoid(np.dot(X[i], w) + b)
p[i] = f_wb >= 0.5
return p结果展示
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# 支持显示中文
font_path = '/System/Library/Fonts/STHeiti Light.ttc'
custom_font = fm.FontProperties(fname=font_path)
plt.rcParams["font.family"] = custom_font.get_name()
# 载入训练集
X_train, y_train = load_data("data/ex2data1.txt")
# 训练模型
np.random.seed(1)
intial_w = 0.01 * (np.random.rand(2).reshape(-1,1) - 0.5)
initial_b = -8
iterations = 10000
alpha = 0.001
w_out, b_out, J_history,_ = gradient_descent(X_train ,y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations, 0)
# 根据训练结果(w_out和b_out)计算决策边界
#f = w0*x0 + w1*x1 + b
# x1 = -1 * (w0*x0 + b) / w1
plot_x = np.array([min(X_train[:, 0]), max(X_train[:, 0])])
plot_y = (-1. / w_out[1]) * (w_out[0] * plot_x + b_out)
# 将训练数据分类
x0s_pos = []
x1s_pos = []
x0s_neg = []
x1s_neg = []
for i in range(len(X_train)):
x = X_train[i]
# print(x)
y_i = y_train[i]
if y_i == 1:
x0s_pos.append(x[0])
x1s_pos.append(x[1])
else:
x0s_neg.append(x[0])
x1s_neg.append(x[1])
# 绘图
plt.figure(figsize=(8, 6))
plt.scatter(x0s_pos, x1s_pos, marker='o', c='green', label="Admitted")
plt.scatter(x0s_neg, x1s_neg, marker='x', c='red', label="Not admitted")
plt.plot(plot_x, plot_y, lw=1, label="决策边界")
plt.xlabel('Exam 1 score', fontsize=12)
plt.ylabel('Exam 2 score', fontsize=12)
plt.title('在二维平面上可视化分类模型的决策边界', fontsize=14)
plt.legend(fontsize=12, loc='upper center')
plt.grid(True)
plt.show()
# 使用训练集计算预测准确率
p = predict(X_train, w_out, b_out)
print('Train Accuracy: %f'%(np.mean(p == y_train) * 100))
# Train Accuracy: 92.000000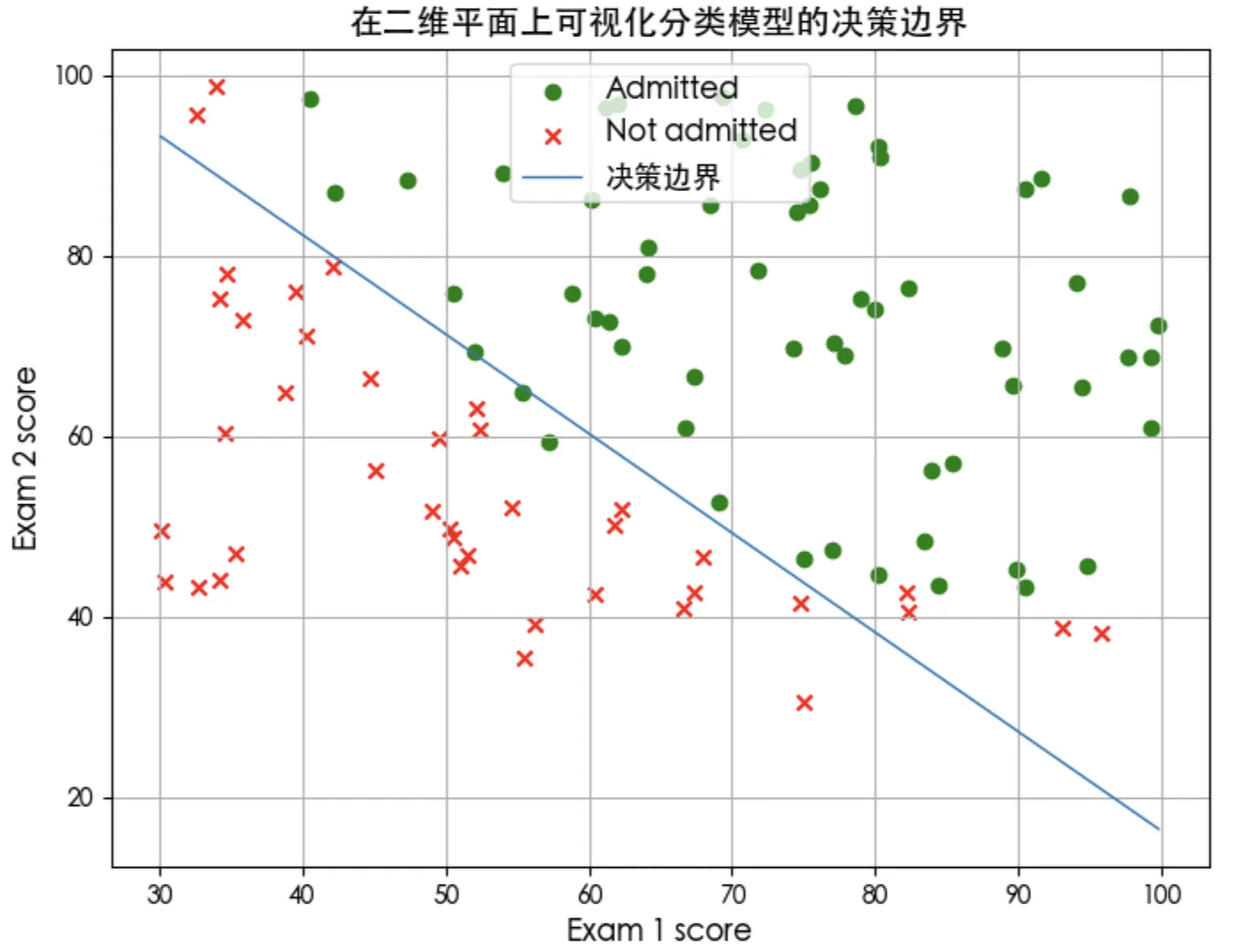
正则化逻辑回归实战
模型选择
可视化训练数据,基于此数据选择多项式逻辑回归模型
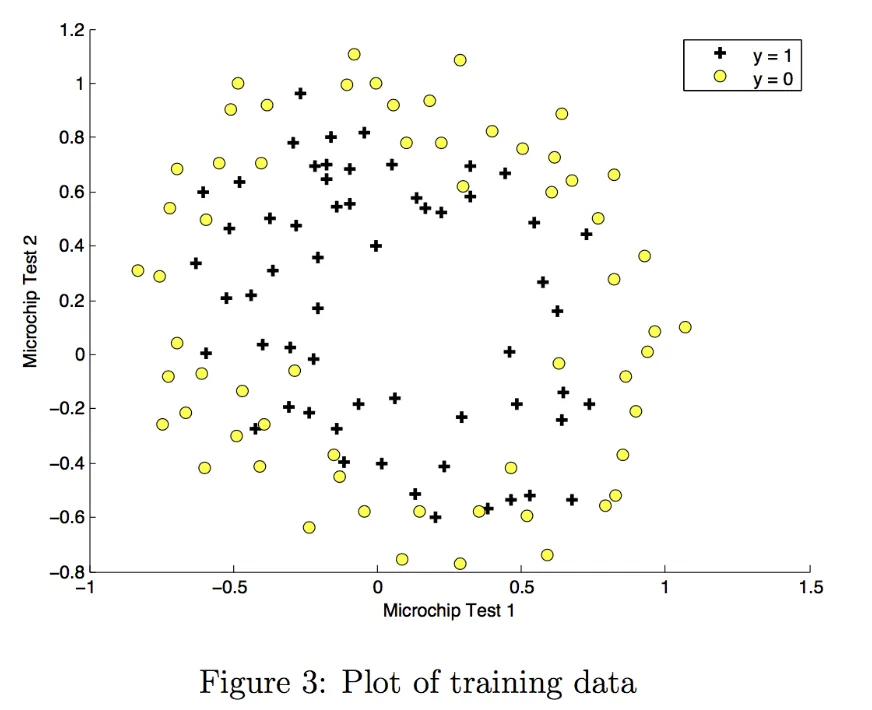
关键代码实现
由于要拟合非线性决策边界,所以要增加特征的复杂度(训练数据里只有2个特征)。
特征映射函数
# 将输入特征 X1 和 X2 转换为六次多项式特征
# 这个函数常用于逻辑回归或支持向量机等模型中,通过增加特征的复杂度来拟合非线性决策边界。
def map_feature(X1, X2):
"""
Feature mapping function to polynomial features
"""
X1 = np.atleast_1d(X1)
X2 = np.atleast_1d(X2)
degree = 6
out = []
for i in range(1, degree+1):
for j in range(i + 1):
out.append((X1**(i-j) * (X2**j)))
return np.stack(out, axis=1)正则化后的损失函数和梯度计算函数
def compute_cost_reg(X, y, w, b, lambda_ = 1):
"""
Computes the cost over all examples
Args:
X : (array_like Shape (m,n)) data, m examples by n features
y : (array_like Shape (m,)) target value
w : (array_like Shape (n,)) Values of parameters of the model
b : (array_like Shape (n,)) Values of bias parameter of the model
lambda_ : (scalar, float) Controls amount of regularization
Returns:
total_cost: (scalar) cost
"""
m, n = X.shape
# Calls the compute_cost function that you implemented above
cost_without_reg = compute_cost(X, y, w, b)
reg_cost = 0.
for j in range(n):
reg_cost += w[j]**2
# Add the regularization cost to get the total cost
total_cost = cost_without_reg + (lambda_/(2 * m)) * reg_cost
return total_cost
def compute_gradient_reg(X, y, w, b, lambda_ = 1):
"""
Computes the gradient for linear regression
Args:
X : (ndarray Shape (m,n)) variable such as house size
y : (ndarray Shape (m,)) actual value
w : (ndarray Shape (n,)) values of parameters of the model
b : (scalar) value of parameter of the model
lambda_ : (scalar,float) regularization constant
Returns
dj_db: (scalar) The gradient of the cost w.r.t. the parameter b.
dj_dw: (ndarray Shape (n,)) The gradient of the cost w.r.t. the parameters w.
"""
m, n = X.shape
dj_db, dj_dw = compute_gradient(X, y, w, b)
# Add the regularization
for j in range(n):
dj_dw[j] += (lambda_ / m) * w[j]
return dj_db, dj_dw结果展示
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# 支持显示中文
font_path = '/System/Library/Fonts/STHeiti Light.ttc'
custom_font = fm.FontProperties(fname=font_path)
plt.rcParams["font.family"] = custom_font.get_name()
# 载入训练集
X_train, y_train = load_data("data/ex2data2.txt")
# 通过增加特征的复杂度来拟合非线性决策边界
X_mapped = map_feature(X_train[:, 0], X_train[:, 1])
print("Original shape of data:", X_train.shape)
print("Shape after feature mapping:", X_mapped.shape)
# 训练模型
np.random.seed(1)
initial_w = np.random.rand(X_mapped.shape[1])-0.5
initial_b = 1.
# Set regularization parameter lambda_ to 1 (you can try varying this)
lambda_ = 0.5
iterations = 10000
alpha = 0.01
w_out, b_out, J_history, _ = gradient_descent(X_mapped, y_train, initial_w, initial_b, compute_cost_reg, compute_gradient_reg, alpha, iterations, lambda_)
# 根据训练结果(w_out和b_out)计算决策边界
# - 创建网格点 u 和 v 覆盖特征空间
u = np.linspace(-1, 1.5, 50)
v = np.linspace(-1, 1.5, 50)
# - 计算每个网格点处的预测概率 z
z = np.zeros((len(u), len(v)))
# Evaluate z = theta*x over the grid
for i in range(len(u)):
for j in range(len(v)):
z[i,j] = sig(np.dot(map_feature(u[i], v[j]), w_out) + b_out)
# - 转置 z 是必要的,因为contour函数期望的输入格式与我们的计算顺序不一致
z = z.T
# 分类
x0s_pos = []
x1s_pos = []
x0s_neg = []
x1s_neg = []
for i in range(len(X_train)):
x = X_train[i]
# print(x)
y_i = y_train[i]
if y_i == 1:
x0s_pos.append(x[0])
x1s_pos.append(x[1])
else:
x0s_neg.append(x[0])
x1s_neg.append(x[1])
# 绘图
plt.figure(figsize=(8, 6))
plt.scatter(x0s_pos, x1s_pos, marker='o', c='black', label="y=1")
plt.scatter(x0s_neg, x1s_neg, marker='x', c='orange', label="y=0")
# 绘制决策边界(等高线)
plt.contour(u,v,z, levels = [0.5], colors="green")
# 创建虚拟线条用于图例(颜色和线型需与等高线一致)
plt.plot([], [], color='green', label="决策边界")
plt.xlabel('Test 1', fontsize=12)
plt.ylabel('Test 2', fontsize=12)
plt.title('正则化逻辑回归模型分类效果可视化(lambda=0.5)', fontsize=14)
# plt.legend(fontsize=12, loc='upper center')
plt.legend(fontsize=12)
plt.grid(True)
plt.show()
#Compute accuracy on the training set
p = predict(X_mapped, w_out, b_out)
print('Train Accuracy: %f'%(np.mean(p == y_train) * 100))
# Train Accuracy: 83.050847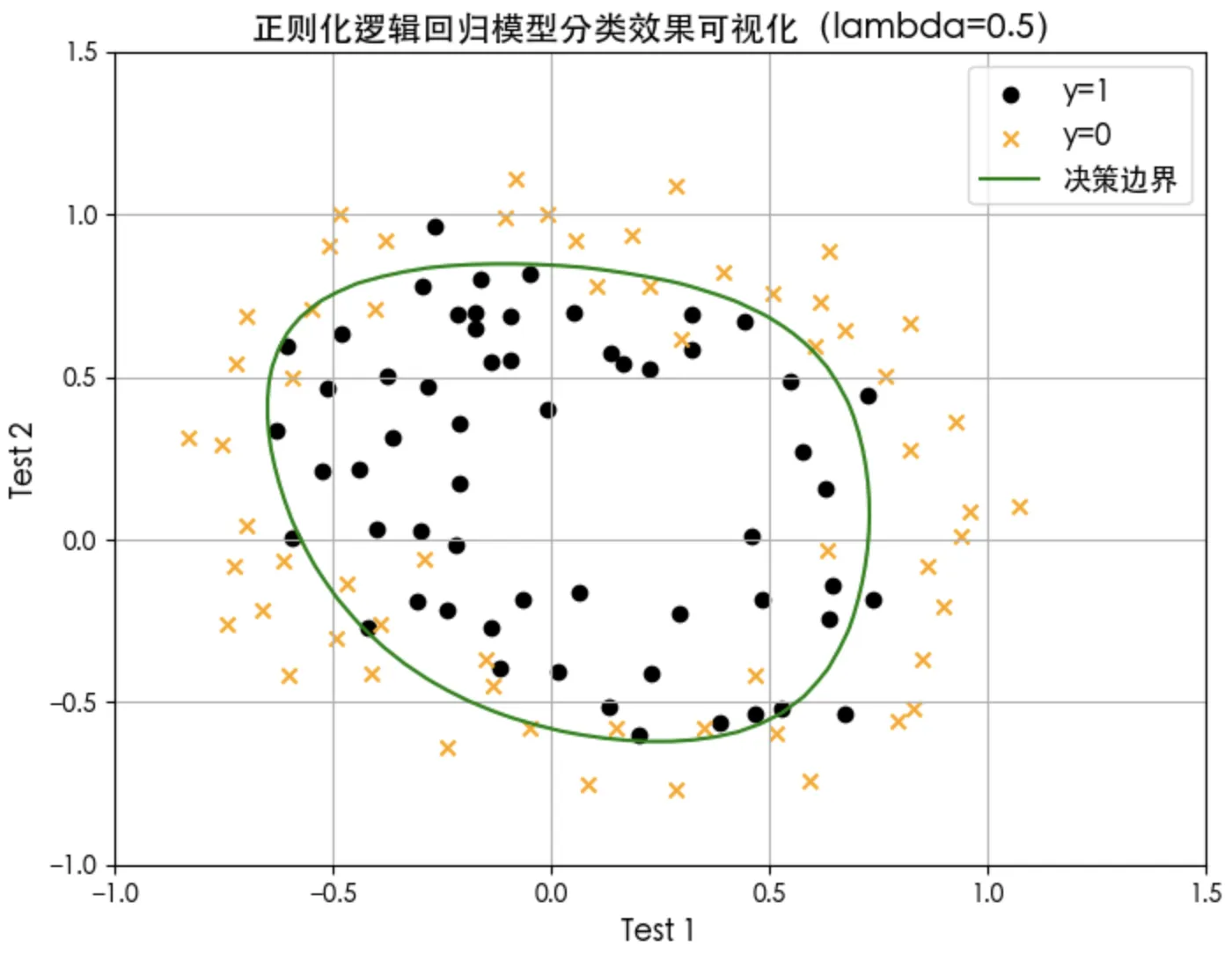
正则化效果对比
正则化对损失和决策边界的影响
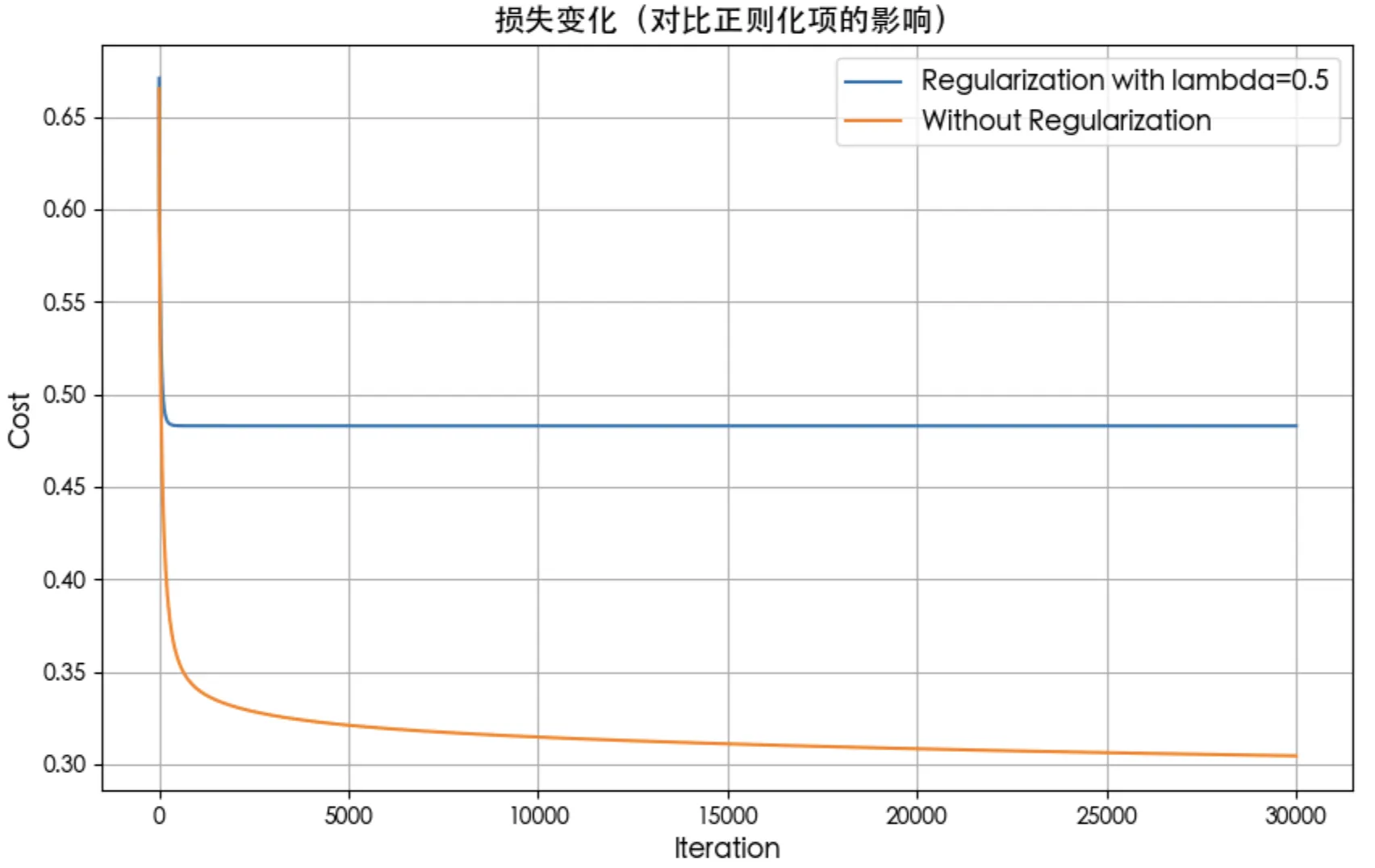
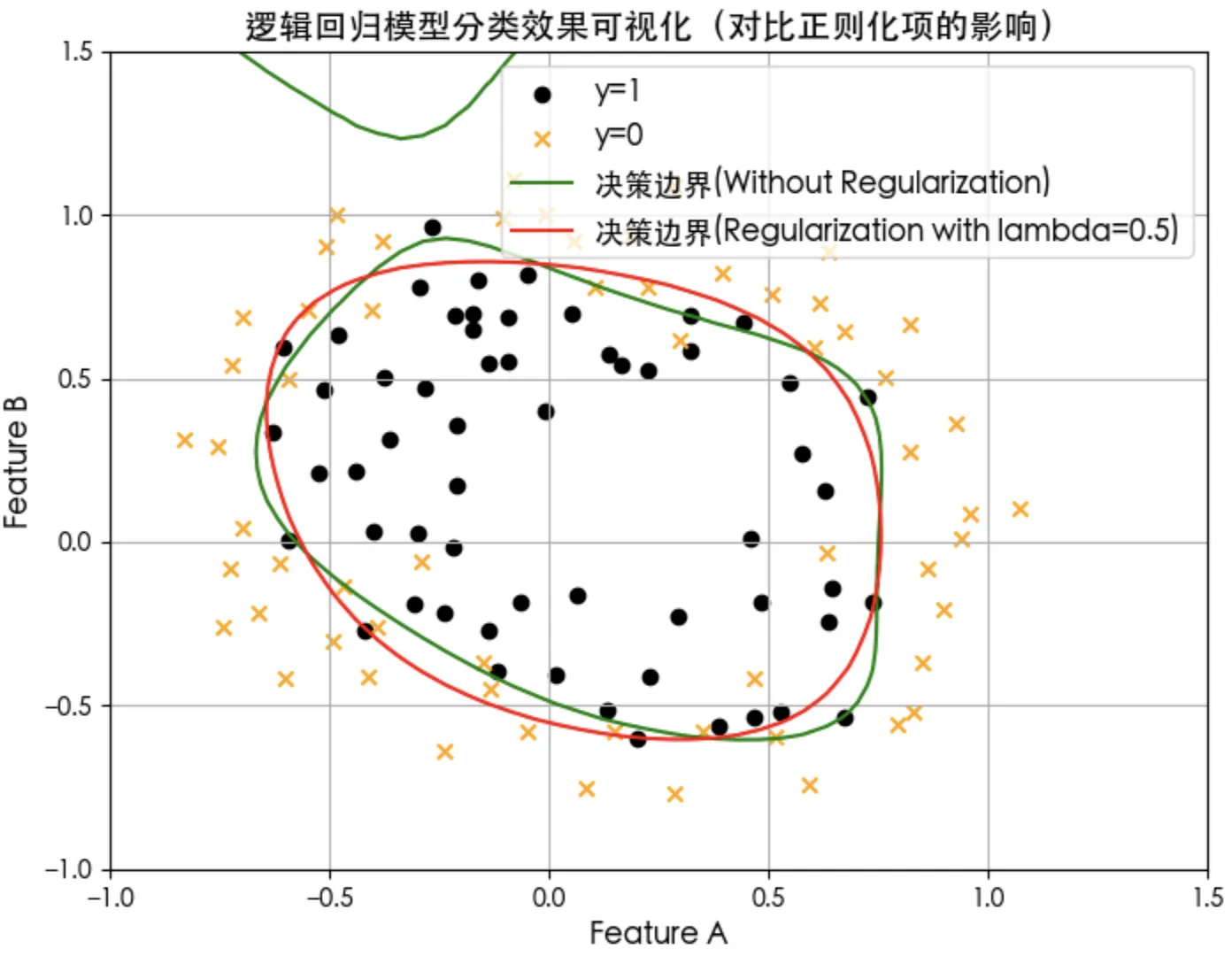
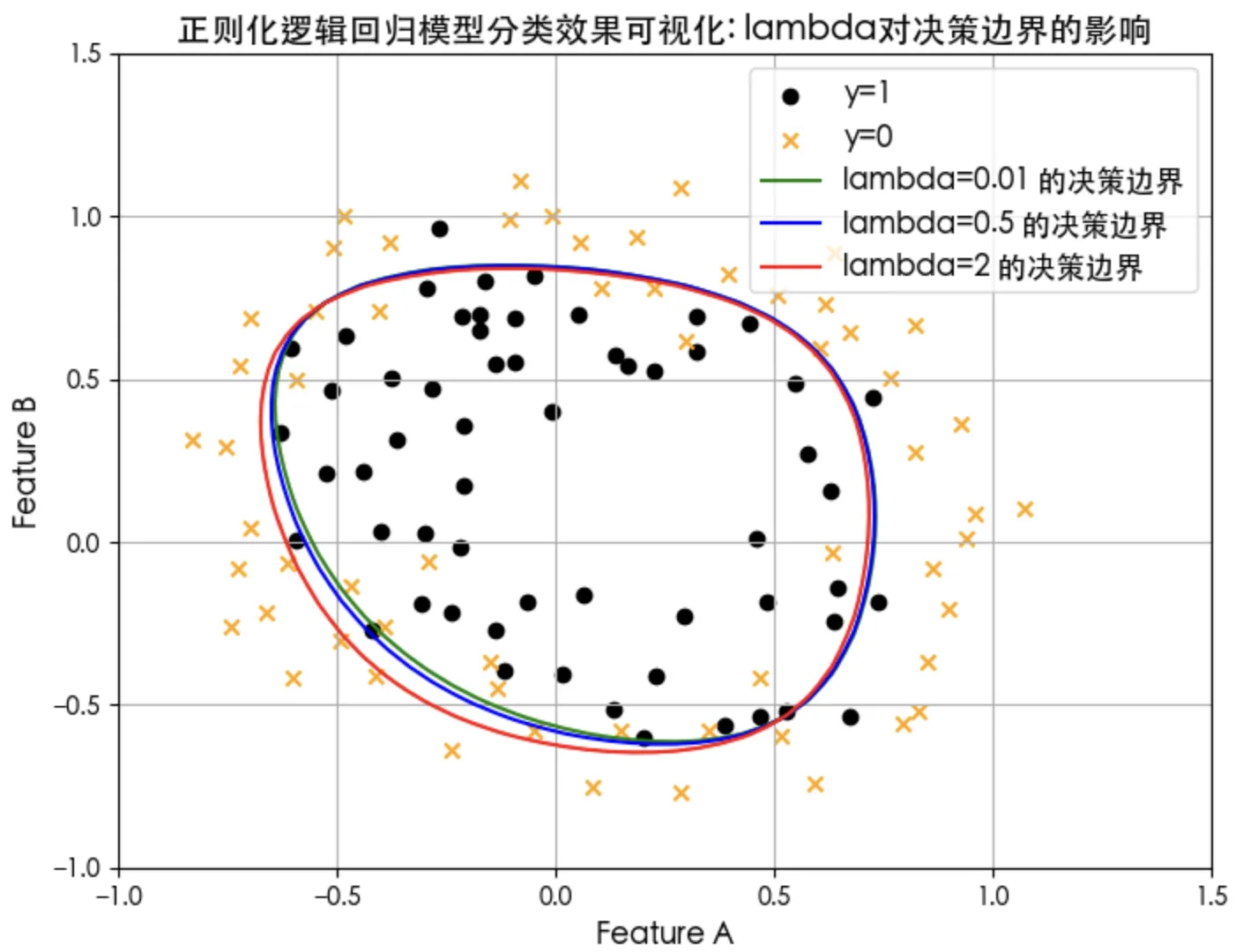
正则化项lambda参数大小对决策边界的影响
参考
吴恩达团队在Coursera开设的机器学习课程:https://www.coursera.org/specializations/machine-learning-introduction