【华为机试】547. 省份数量

熬了夜的程序员2025-07-24 14:11

文章目录

547. 省份数量

描述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1

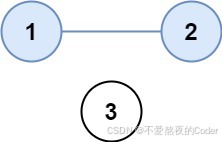
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]

输出：2

示例 2

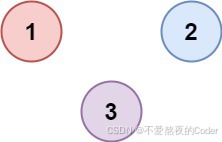
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]

输出：3

提示

  • 1 <= n <= 200
  • n == isConnected.length
  • n == isConnected[i].length
  • isConnected[i][j] 为 1 或 0
  • isConnected[i][i] == 1
  • isConnected[i][j] == isConnected[j][i]

解题思路

核心分析

这道题是一个经典的图论连通性问题。核心思想是计算无向图中连通分量的数量。

问题本质：给定一个无向图的邻接矩阵，计算图中连通分量的个数。

关键洞察：

  • 每个城市是一个节点，城市间的连接关系构成边
  • 省份就是连通分量，即相互可达的节点集合
  • 可以通过遍历算法（DFS/BFS）或并查集来求解

问题转化

原始问题：计算n个城市中省份的数量

图论转化：

  1. 将城市抽象为图中的节点
  2. 将城市间的连接关系抽象为图中的边
  3. 省份数量 = 连通分量数量

数学建模：

  • 节点集合：V = {0, 1, 2, ..., n-1}
  • 边集合：E = {(i, j) | isConnected[i][j] = 1}
  • 目标：计算图G(V, E)中连通分量的数量

算法选择策略

1. 深度优先搜索 (DFS)
  • 适用场景：连通性问题，需要遍历所有可达节点
  • 优势：实现简单，递归清晰，空间效率高
  • 劣势：可能栈溢出，不适合极大数据量
2. 广度优先搜索 (BFS)
  • 适用场景：连通性问题，需要层次遍历
  • 优势：避免栈溢出，适合大数据量
  • 劣势：需要队列空间，实现稍复杂
3. 并查集 (Union-Find)
  • 适用场景：动态连通性问题，需要频繁合并操作
  • 优势：支持动态操作，理论复杂度最优
  • 劣势：实现复杂，常数项较大

算法实现详解

方法一：深度优先搜索 (DFS)

核心思想：从每个未访问的节点开始，递归访问所有可达节点

算法步骤：

  1. 初始化访问数组visited，记录每个节点是否被访问
  2. 遍历所有节点，对每个未访问的节点：
    • 调用DFS函数访问该节点及其所有可达节点
    • 连通分量数量加1
  3. DFS函数实现：
    • 标记当前节点为已访问
    • 遍历所有与当前节点相连的节点
    • 对每个未访问的相连节点递归调用DFS

代码实现：

go 复制代码 
func findCircleNumDFS(isConnected [][]int) int {
    n := len(isConnected)
    if n == 0 {
        return 0
    }

    visited := make([]bool, n)
    count := 0

    for i := 0; i < n; i++ {
        if !visited[i] {
            dfs(isConnected, visited, i)
            count++
        }
    }

    return count
}

func dfs(isConnected [][]int, visited []bool, city int) {
    visited[city] = true
    
    for nextCity := 0; nextCity < len(isConnected); nextCity++ {
        if isConnected[city][nextCity] == 1 && !visited[nextCity] {
            dfs(isConnected, visited, nextCity)
        }
    }
}

时间复杂度分析：

  • 每个节点最多被访问一次：O(n)
  • 每次访问需要遍历所有相邻节点：O(n)
  • 总时间复杂度：O(n²)

空间复杂度分析：

  • 访问数组：O(n)
  • 递归调用栈深度：O(n)
  • 总空间复杂度：O(n)
方法二：广度优先搜索 (BFS)

核心思想：使用队列进行层次遍历，访问所有可达节点

算法步骤：

  1. 初始化访问数组和队列
  2. 遍历所有节点，对每个未访问的节点：
    • 将节点加入队列
    • 标记为已访问
    • 连通分量数量加1
    • 执行BFS遍历
  3. BFS函数实现：
    • 从队列中取出节点
    • 遍历所有与当前节点相连的节点
    • 将未访问的相连节点加入队列并标记为已访问

代码实现：

go 复制代码 
func findCircleNumBFS(isConnected [][]int) int {
    n := len(isConnected)
    if n == 0 {
        return 0
    }

    visited := make([]bool, n)
    count := 0

    for i := 0; i < n; i++ {
        if !visited[i] {
            bfs(isConnected, visited, i)
            count++
        }
    }

    return count
}

func bfs(isConnected [][]int, visited []bool, startCity int) {
    queue := []int{startCity}
    visited[startCity] = true

    for len(queue) > 0 {
        city := queue[0]
        queue = queue[1:]

        for nextCity := 0; nextCity < len(isConnected); nextCity++ {
            if isConnected[city][nextCity] == 1 && !visited[nextCity] {
                visited[nextCity] = true
                queue = append(queue, nextCity)
            }
        }
    }
}

时间复杂度 ：O(n²)
空间复杂度：O(n)

方法三：并查集 (Union-Find)

核心思想：使用并查集维护连通性，通过合并操作统计连通分量

算法步骤：

  1. 初始化并查集，每个节点自成一个集合
  2. 遍历邻接矩阵，对每个连接关系：
    • 合并相连的两个节点到同一集合
  3. 统计最终集合的数量

并查集优化：

  • 路径压缩：在查找时压缩路径，减少后续查找时间
  • 按秩合并：将较小的树合并到较大的树上，保持树的平衡

代码实现：

go 复制代码 
type UnionFind struct {
    parent []int
    rank   []int
    count  int
}

func NewUnionFind(n int) *UnionFind {
    parent := make([]int, n)
    rank := make([]int, n)
    
    for i := 0; i < n; i++ {
        parent[i] = i
        rank[i] = 1
    }

    return &UnionFind{
        parent: parent,
        rank:   rank,
        count:  n,
    }
}

func (uf *UnionFind) Find(x int) int {
    if uf.parent[x] != x {
        uf.parent[x] = uf.Find(uf.parent[x]) // 路径压缩
    }
    return uf.parent[x]
}

func (uf *UnionFind) Union(x, y int) {
    rootX := uf.Find(x)
    rootY := uf.Find(y)
    
    if rootX == rootY {
        return
    }

    // 按秩合并
    if uf.rank[rootX] < uf.rank[rootY] {
        uf.parent[rootX] = rootY
    } else if uf.rank[rootX] > uf.rank[rootY] {
        uf.parent[rootY] = rootX
    } else {
        uf.parent[rootY] = rootX
        uf.rank[rootX]++
    }
    
    uf.count--
}

func (uf *UnionFind) Count() int {
    return uf.count
}

时间复杂度 ：O(n² × α(n))，其中α(n)是阿克曼函数的反函数
空间复杂度：O(n)

算法选择

1. 深度优先搜索 (DFS)
  • 时间复杂度：O(n²)，其中 n 是城市数量
  • 空间复杂度：O(n)，递归调用栈的深度
  • 适用场景：适合处理连通性问题
2. 广度优先搜索 (BFS)
  • 时间复杂度：O(n²)
  • 空间复杂度：O(n)，队列的空间
  • 适用场景：适合处理连通性问题，避免递归栈溢出
3. 并查集 (Union-Find)
  • 时间复杂度：O(n² × α(n))，其中 α(n) 是阿克曼函数的反函数
  • 空间复杂度：O(n)
  • 适用场景：适合处理动态连通性问题

数学证明

并查集正确性证明

定理：并查集算法能正确计算连通分量的数量。

证明：

  1. 初始化正确性：

    • 初始时每个节点自成一个集合
    • 集合数量等于节点数量

  2. 合并操作正确性：

    • 每次合并操作将两个连通分量合并为一个
    • 集合数量减少1

  3. 最终结果正确性：

    • 所有相连的节点都在同一集合中
    • 不同连通分量的节点在不同集合中
    • 集合数量等于连通分量数量
时间复杂度分析

定理：并查集算法的时间复杂度为O(n² × α(n))。

证明：

  • 每个节点最多参与n次合并操作
  • 每次合并操作的时间复杂度为O(α(n))
  • 总时间复杂度为O(n² × α(n))

执行流程图

否 是 否 是 否 是 否 是 是 否 否 是 开始: 输入邻接矩阵 选择算法 DFS算法 BFS算法 并查集算法 初始化访问数组 遍历所有节点 节点是否已访问? 调用DFS函数 继续下一个节点 连通分量数量+1 是否遍历完成? 返回结果 初始化访问数组和队列 遍历所有节点 节点是否已访问? 调用BFS函数 继续下一个节点 连通分量数量+1 是否遍历完成? 初始化并查集 遍历邻接矩阵 是否存在连接? 合并两个节点 继续下一个元素 是否遍历完成? 返回集合数量 结束

算法可视化

DFS遍历过程 图结构 邻接矩阵 访问城市0 访问城市1 连通分量1完成 访问城市2 连通分量2完成 城市1 城市0 城市2 1 1 0 1 1 0 0 0 1

实际应用

  1. 社交网络分析：计算朋友圈的数量
  2. 网络拓扑分析：计算网络中的连通区域
  3. 地理信息系统：计算地理区域的连通性
  4. 电路设计：分析电路的连通性
  5. 生物信息学：分析蛋白质相互作用网络

算法优化技巧

1. 内存优化
go 复制代码 
// 使用位运算优化访问数组
visited := make([]uint64, (n+63)/64)
2. 早期终止
go 复制代码 
// 如果所有节点都已访问，可以提前终止
if count == n {
    return 1
}
3. 对称性利用
go 复制代码 
// 利用邻接矩阵的对称性，只遍历上三角
for i := 0; i < n; i++ {
    for j := i + 1; j < n; j++ {
        if isConnected[i][j] == 1 {
            // 处理连接关系
        }
    }
}

扩展思考

  1. 有向图：如果是有向图，如何计算强连通分量？
  2. 加权图：如果边有权重，如何定义连通性？
  3. 动态图：如果图结构动态变化，如何维护连通性？
  4. 大规模图：对于超大规模图，如何优化算法？
  5. 并行算法：如何设计并行版本的连通分量算法？

相关问题

  1. 200. 岛屿数量：二维网格中的连通分量问题
  2. 130. 被围绕的区域：连通分量的边界处理
  3. 399. 除法求值：带权图的连通性问题
  4. 684. 冗余连接：并查集在最小生成树中的应用
  5. 685. 冗余连接 II：有向图的连通性问题

测试用例设计

go 复制代码 
// 基础测试用例
isConnected1 := [][]int{
    {1, 1, 0},
    {1, 1, 0},
    {0, 0, 1},
}
expected1 := 2

isConnected2 := [][]int{
    {1, 0, 0},
    {0, 1, 0},
    {0, 0, 1},
}
expected2 := 3

// 边界测试
isConnected3 := [][]int{{1}}
expected3 := 1

var isConnected4 [][]int
expected4 := 0

// 极值测试
isConnected5 := [][]int{
    {1, 1, 1},
    {1, 1, 1},
    {1, 1, 1},
}
expected5 := 1

// 复杂情况
isConnected6 := [][]int{
    {1, 0, 0, 1},
    {0, 1, 1, 0},
    {0, 1, 1, 1},
    {1, 0, 1, 1},
}
expected6 := 1

性能对比

算法 时间复杂度 空间复杂度 常数项 适用场景
DFS O(n²) O(n) 小 一般情况
BFS O(n²) O(n) 中等 大数据量
并查集 O(n² × α(n)) O(n) 大 动态连通性

常见错误

  1. 访问标记错误：忘记标记节点为已访问
  2. 递归终止错误：递归函数没有正确的终止条件
  3. 数组越界：访问邻接矩阵时越界
  4. 并查集初始化错误：parent数组初始化不正确
  5. 边界处理错误：没有正确处理空矩阵或单个节点

总结

省份数量 是一道经典的图论连通性问题，核心在于理解连通分量的概念和计算算法。

最优解法 是DFS或BFS算法，具有以下优势：

  1. 时间复杂度合理：O(n²)
  2. 实现简单：递归或队列遍历
  3. 空间效率高：只需要O(n)额外空间
  4. 应用广泛：是图遍历的经典模板题

这道题体现了图论算法中的重要思想：

  • 连通性分析：通过遍历确定节点间的可达性
  • 访问标记：避免重复访问，提高算法效率
  • 问题建模：将实际问题抽象为图论问题

并查集算法虽然理论复杂度最优，但在实际应用中，由于常数项较大，对于中等规模的问题，DFS/BFS算法往往更实用。

算法流程图

否 是 否 是 否 是 否 是 开始 初始化访问数组 visited 遍历所有城市 i 城市 i 是否已访问? DFS/BFS 遍历连通分量 继续下一个城市 省份数量 + 1 是否遍历完所有城市? 返回省份数量 结束 标记当前城市为已访问 遍历所有相邻城市 相邻城市是否已访问? 递归访问相邻城市 继续下一个相邻城市 是否遍历完所有相邻城市? 返回

详细解题步骤

方法一：深度优先搜索 (DFS)
  1. 初始化 ：创建访问数组 visited，记录每个城市是否被访问过
  2. 遍历城市：从每个未访问的城市开始进行DFS
  3. DFS过程 ：
    • 标记当前城市为已访问
    • 遍历所有与当前城市相连的城市
    • 对每个未访问的相连城市递归调用DFS
  4. 计数：每次开始新的DFS时，省份数量加1
方法二：广度优先搜索 (BFS)
  1. 初始化：创建访问数组和队列
  2. 遍历城市：从每个未访问的城市开始进行BFS
  3. BFS过程 ：
    • 将当前城市加入队列
    • 标记为已访问
    • 从队列中取出城市，遍历其所有相连城市
    • 将未访问的相连城市加入队列
  4. 计数：每次开始新的BFS时，省份数量加1
方法三：并查集 (Union-Find)
  1. 初始化：创建并查集，每个城市自成一个集合
  2. 合并操作：遍历邻接矩阵，将相连的城市合并到同一集合
  3. 统计集合：统计最终有多少个不同的集合

复杂度分析

方法 时间复杂度 空间复杂度 优势 劣势
DFS O(n²) O(n) 实现简单，递归清晰 可能栈溢出
BFS O(n²) O(n) 避免栈溢出 需要队列
并查集 O(n² × α(n)) O(n) 适合动态连通性 实现复杂

边界情况处理

  1. 空矩阵：返回0
  2. 单个城市：返回1
  3. 所有城市都不相连：返回n
  4. 所有城市都相连：返回1

优化技巧

  1. 提前返回：如果所有城市都已访问，可以提前结束
  2. 对称性利用：由于是无向图，邻接矩阵是对称的
  3. 内存优化：使用位运算优化访问数组的存储

完整题解代码

go 复制代码 
package main

import (
	"fmt"
)

// 方法一：深度优先搜索 (DFS)
// 时间复杂度：O(n²)，空间复杂度：O(n)
func findCircleNumDFS(isConnected [][]int) int {
	n := len(isConnected)
	if n == 0 {
		return 0
	}

	// 访问数组，记录每个城市是否被访问过
	visited := make([]bool, n)
	count := 0

	// 从每个未访问的城市开始DFS
	for i := 0; i < n; i++ {
		if !visited[i] {
			dfs(isConnected, visited, i)
			count++
		}
	}

	return count
}

// DFS辅助函数
func dfs(isConnected [][]int, visited []bool, city int) {
	visited[city] = true
	
	// 遍历所有与当前城市相连的城市
	for nextCity := 0; nextCity < len(isConnected); nextCity++ {
		if isConnected[city][nextCity] == 1 && !visited[nextCity] {
			dfs(isConnected, visited, nextCity)
		}
	}
}

// 方法二：广度优先搜索 (BFS)
// 时间复杂度：O(n²)，空间复杂度：O(n)
func findCircleNumBFS(isConnected [][]int) int {
	n := len(isConnected)
	if n == 0 {
		return 0
	}

	visited := make([]bool, n)
	count := 0

	// 从每个未访问的城市开始BFS
	for i := 0; i < n; i++ {
		if !visited[i] {
			bfs(isConnected, visited, i)
			count++
		}
	}

	return count
}

// BFS辅助函数
func bfs(isConnected [][]int, visited []bool, startCity int) {
	queue := []int{startCity}
	visited[startCity] = true

	for len(queue) > 0 {
		city := queue[0]
		queue = queue[1:]

		// 遍历所有与当前城市相连的城市
		for nextCity := 0; nextCity < len(isConnected); nextCity++ {
			if isConnected[city][nextCity] == 1 && !visited[nextCity] {
				visited[nextCity] = true
				queue = append(queue, nextCity)
			}
		}
	}
}

// 方法三：并查集 (Union-Find)
// 时间复杂度：O(n² × α(n))，空间复杂度：O(n)
func findCircleNumUnionFind(isConnected [][]int) int {
	n := len(isConnected)
	if n == 0 {
		return 0
	}

	// 初始化并查集
	uf := NewUnionFind(n)

	// 遍历邻接矩阵，合并相连的城市
	for i := 0; i < n; i++ {
		for j := i + 1; j < n; j++ { // 利用对称性，只遍历上三角
			if isConnected[i][j] == 1 {
				uf.Union(i, j)
			}
		}
	}

	return uf.Count()
}

// 并查集结构
type UnionFind struct {
	parent []int
	rank   []int
	count  int
}

// 创建新的并查集
func NewUnionFind(n int) *UnionFind {
	parent := make([]int, n)
	rank := make([]int, n)
	
	for i := 0; i < n; i++ {
		parent[i] = i
		rank[i] = 1
	}

	return &UnionFind{
		parent: parent,
		rank:   rank,
		count:  n,
	}
}

// 查找根节点（路径压缩）
func (uf *UnionFind) Find(x int) int {
	if uf.parent[x] != x {
		uf.parent[x] = uf.Find(uf.parent[x]) // 路径压缩
	}
	return uf.parent[x]
}

// 合并两个集合（按秩合并）
func (uf *UnionFind) Union(x, y int) {
	rootX := uf.Find(x)
	rootY := uf.Find(y)
	
	if rootX == rootY {
		return
	}

	// 按秩合并
	if uf.rank[rootX] < uf.rank[rootY] {
		uf.parent[rootX] = rootY
	} else if uf.rank[rootX] > uf.rank[rootY] {
		uf.parent[rootY] = rootX
	} else {
		uf.parent[rootY] = rootX
		uf.rank[rootX]++
	}
	
	uf.count--
}

// 返回集合数量
func (uf *UnionFind) Count() int {
	return uf.count
}

// 方法四：优化的DFS（使用栈避免递归）
// 时间复杂度：O(n²)，空间复杂度：O(n)
func findCircleNumDFSIterative(isConnected [][]int) int {
	n := len(isConnected)
	if n == 0 {
		return 0
	}

	visited := make([]bool, n)
	count := 0

	for i := 0; i < n; i++ {
		if !visited[i] {
			dfsIterative(isConnected, visited, i)
			count++
		}
	}

	return count
}

// 迭代式DFS
func dfsIterative(isConnected [][]int, visited []bool, startCity int) {
	stack := []int{startCity}
	visited[startCity] = true

	for len(stack) > 0 {
		city := stack[len(stack)-1]
		stack = stack[:len(stack)-1]

		for nextCity := 0; nextCity < len(isConnected); nextCity++ {
			if isConnected[city][nextCity] == 1 && !visited[nextCity] {
				visited[nextCity] = true
				stack = append(stack, nextCity)
			}
		}
	}
}

// 测试函数
func main() {
	// 测试用例1：示例1
	isConnected1 := [][]int{
		{1, 1, 0},
		{1, 1, 0},
		{0, 0, 1},
	}
	fmt.Println("测试用例1:")
	fmt.Printf("输入: %v\n", isConnected1)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected1))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected1))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected1))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected1))
	fmt.Println("期望结果: 2")
	fmt.Println()

	// 测试用例2：示例2
	isConnected2 := [][]int{
		{1, 0, 0},
		{0, 1, 0},
		{0, 0, 1},
	}
	fmt.Println("测试用例2:")
	fmt.Printf("输入: %v\n", isConnected2)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected2))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected2))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected2))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected2))
	fmt.Println("期望结果: 3")
	fmt.Println()

	// 测试用例3：所有城市相连
	isConnected3 := [][]int{
		{1, 1, 1},
		{1, 1, 1},
		{1, 1, 1},
	}
	fmt.Println("测试用例3 (所有城市相连):")
	fmt.Printf("输入: %v\n", isConnected3)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected3))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected3))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected3))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected3))
	fmt.Println("期望结果: 1")
	fmt.Println()

	// 测试用例4：单个城市
	isConnected4 := [][]int{{1}}
	fmt.Println("测试用例4 (单个城市):")
	fmt.Printf("输入: %v\n", isConnected4)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected4))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected4))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected4))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected4))
	fmt.Println("期望结果: 1")
	fmt.Println()

	// 测试用例5：空矩阵
	var isConnected5 [][]int
	fmt.Println("测试用例5 (空矩阵):")
	fmt.Printf("输入: %v\n", isConnected5)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected5))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected5))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected5))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected5))
	fmt.Println("期望结果: 0")
	fmt.Println()

	// 测试用例6：复杂情况
	isConnected6 := [][]int{
		{1, 0, 0, 1},
		{0, 1, 1, 0},
		{0, 1, 1, 1},
		{1, 0, 1, 1},
	}
	fmt.Println("测试用例6 (复杂情况):")
	fmt.Printf("输入: %v\n", isConnected6)
	fmt.Printf("DFS结果: %d\n", findCircleNumDFS(isConnected6))
	fmt.Printf("BFS结果: %d\n", findCircleNumBFS(isConnected6))
	fmt.Printf("并查集结果: %d\n", findCircleNumUnionFind(isConnected6))
	fmt.Printf("迭代DFS结果: %d\n", findCircleNumDFSIterative(isConnected6))
	fmt.Println("期望结果: 1")
}
相关推荐
JXL186040 分钟前
Leetcode-.42接雨水
算法·leetcode·职场和发展
啊我不会诶2 小时前
CF每日5题(1500-1600)
c++·学习·算法
自学也学好编程2 小时前
【学习路线】Go语言云原生开发之路：从简洁语法到微服务架构
学习·golang
巴伦是只猫2 小时前
Java 高频算法
java·开发语言·算法
点云SLAM3 小时前
C++中std::string和std::string_view使用详解和示例
开发语言·c++·算法·字符串·string·c++标准库算法·string_view
88号技师3 小时前
2025年7月Renewable Energy-冬虫夏草优化算法Caterpillar Fungus Optimizer-附Matlab免费代码
开发语言·人工智能·算法·matlab·优化算法
dragoooon344 小时前
优选算法：移动零
c++·学习·算法·学习方法
运维小文4 小时前
初探贪心算法 -- 使用最少纸币组成指定金额
c++·python·算法·贪心算法
智者知已应修善业5 小时前
【C# 找最大值、最小值和平均值及大于个数和值】2022-9-23
经验分享·笔记·算法·c#
Python涛哥5 小时前
go语言基础教程：【1】基础语法：变量
开发语言·后端·golang
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致04vue数据变化但页面不变05KGG转MP3工具|非KGM文件|解密音频06Claude Code用不了？来试下Qwen3-Coder加持的Qwen Code吧07这次领先Cursor！体验了Trae 2.0 SOLO 模式，超酷！08Cursor Claude 模型无法使用的解决方法09ChatGPT Agent 完全使用指南：2025年7月最新功能详解10我亲历了2025年最荒谬的前端灾难：一支触控笔"干掉"了全球CSS预处理器