学习⽬标
掌握K-近邻算法实现过程
知道K-近邻算法的距离公式
知道K-近邻算法的超参数K值以及取值问题
知道kd树实现搜索的过程
应⽤KNeighborsClassifier实现分类
知道K-近邻算法的优缺点
知道交叉验证实现过程
知道超参数搜索过程
应⽤GridSearchCV实现算法参数的调优
1.1 K-近邻算法简介
学习⽬标
⽬标
了解什么是KNN算法
知道KNN算法求解过程
**1什么是K-近邻算法
根据你的"邻居"来推断出你的类别
1.1 K-近邻算法(KNN)**概念
K Nearest Neighbor算法⼜叫KNN算法,这个算法是机器学习⾥⾯⼀个⽐较经典的算法, 总体来说KNN算法是相对⽐
较容易理解的算法
定义
如果⼀个样本在特征空间中的k个最相似**(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别,则该样本也属于这个
类别。
来源:KNN算法最早是由Cover和Hart提出的⼀种分类算法
距离公式
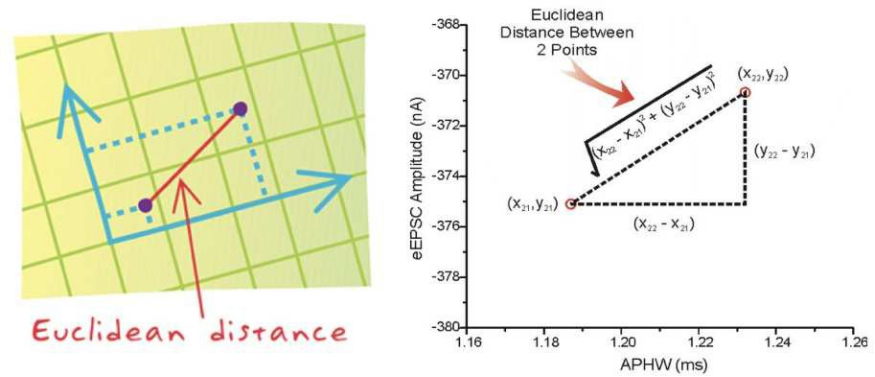
两个样本的距离可以通过如下公式计算,⼜叫欧式距离 ,关于距离公式会在后⾯进⾏讨论
5K-近邻算法简介

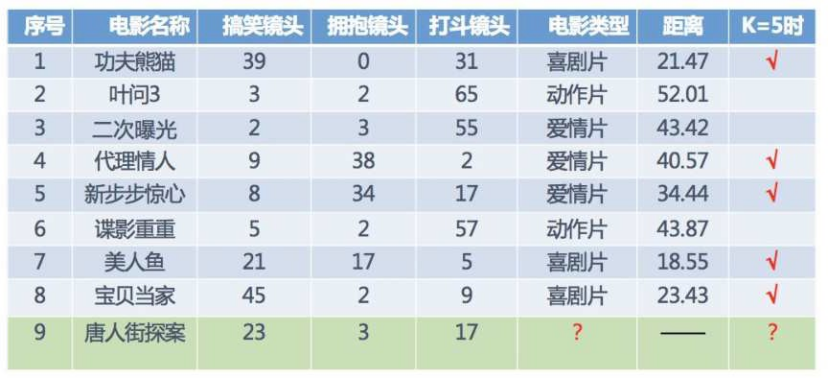
**1.2**电影类型分析**
假设我们现在有⼏部电影
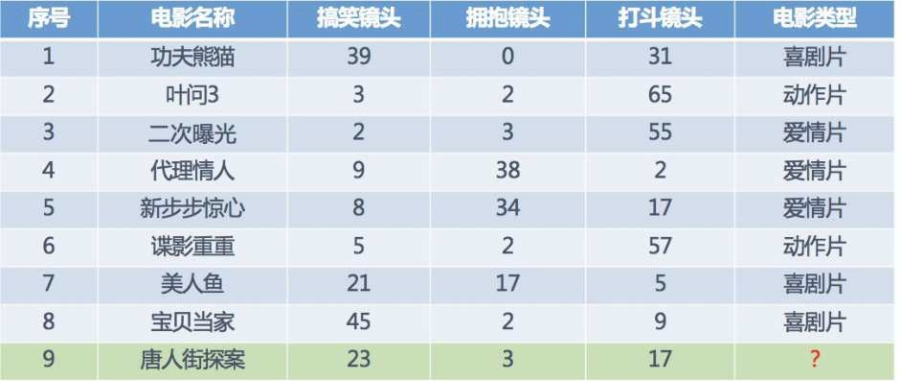
其中? 9号电影不知道类别,如何去预测?我们可以利⽤K近邻算法的思想
分别计算每个电影和被预测电影的距离,然后求解
1.3 KNN****算法流程总结
1)计算已知类别数据集中的点与当前点之间的距离
2)按距离递增次序排序
3)选取与当前点距离最⼩的k个点
4)统计前k个点所在的类别出现的频率
5)返回前k个点出现频率最⾼的类别作为当前点的预测分类
2**⼩结**
7K-近邻算法简介
K-近邻算法简介【了解】
定义:就是通过你的"邻居"来判断你属于哪个类别
如何计算你到你的"邻居"的距离:⼀般时候,都是使⽤欧⽒距离
1.2 k近邻算法api****初步使⽤
学习⽬标
⽬标
了解sklearn⼯具的优点和包含内容
应⽤sklearn中的api实现KNN算法的简单使⽤
机器学习流程复习:
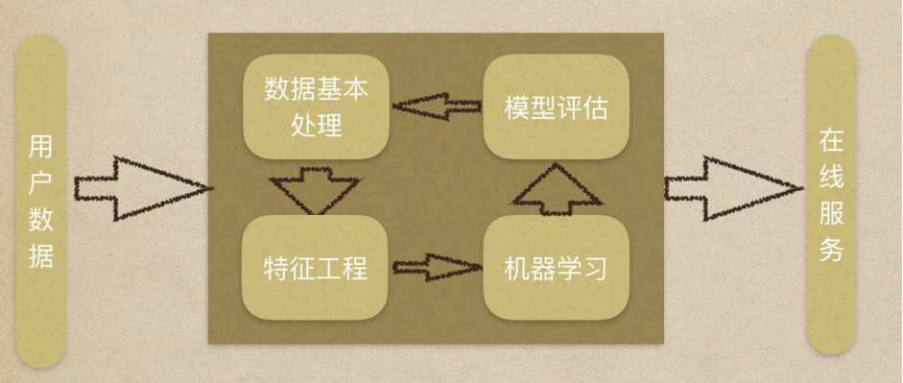
1.获取数据集
2.数据基本处理
3.特征⼯程
4.机器学习
5.模型评估
1 Scikit-learn**⼯具介绍**

Python语⾔的机器学习⼯具
Scikit-learn包括许多知名的机器学习算法的实现
Scikit-learn⽂档完善,容易上⼿,丰富的API
⽬前稳定版本0.19.1
1.1****安装
python
pip3 install scikit-learn==0.19.1安装好之后可以通过以下命令查看是否安装成功
import sklearn
注:安装scikit-learn需要Numpy, Scipy等库
1.2 Scikit-learn****包含的内容

分类、聚类、回归
10k近邻算法api初步使⽤
特征⼯程
模型选择、调优
2 K-近邻算法API
python
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
n_neighbors:int,可选(默认= 5),k_neighbors查询默认使⽤的邻居数3****案例
3.1****步骤分析
1.获取数据集
2.数据基本处理(该案例中省略)
3.特征⼯程(该案例中省略)
4.机器学习
5.模型评估(该案例中省略)
3.2****代码过程
python
导⼊模块
from sklearn.neighbors import KNeighborsClassifier
构造数据集
x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
机器学习 -- 模型训练
# 实例化API
estimator = KNeighborsClassifier(n_neighbors=1)
# 使⽤fit⽅法进⾏训练
estimator.fit(x, y)
estimator.predict([[1]])4**⼩结**
sklearn的优势:
⽂档多,且规范
包含的算法多
实现起来容易
knn中的api
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
问题
1.距离公式,除了欧式距离,还有哪些距离公式可以使⽤?
11k近邻算法api初步使⽤
2.选取K值的⼤⼩?
3.api中其他参数的具体含义?
1.3****距离度量
学习⽬标
⽬标
了解距离公式的基本性质
知道机器学习中常⻅的距离计算公式
1****距离公式的基本性质
在机器学习过程中,对于函数 dist(., .),若它是⼀"距离度量" (distance measure),则需满⾜⼀些基本性质:
⾮负性: dist(X**i, X**j) >= 0 ;
同⼀性:dist(x**i, x**j) = 0。当且仅当 X**i= X**j;
对称性: dist(x**i, x**j) = dist(x**j, x**i);
直递性: dist(x**i, x**j) <= dist(x**i, x**k) + dist(x**k, x**j)
直递性常被直接称为"三⻆不等式"。
2****常⻅的距离公式
2.1欧式距离(Euclidean Distance)****:
欧⽒距离是最容易直观理解的距离度量⽅法,我们⼩学、初中和⾼中接触到的两个点在空间中的距离⼀般都是指欧⽒距 离。

举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1.4142 2.8284 4.2426 1.4142 2.8284 1.4142
13距离度量
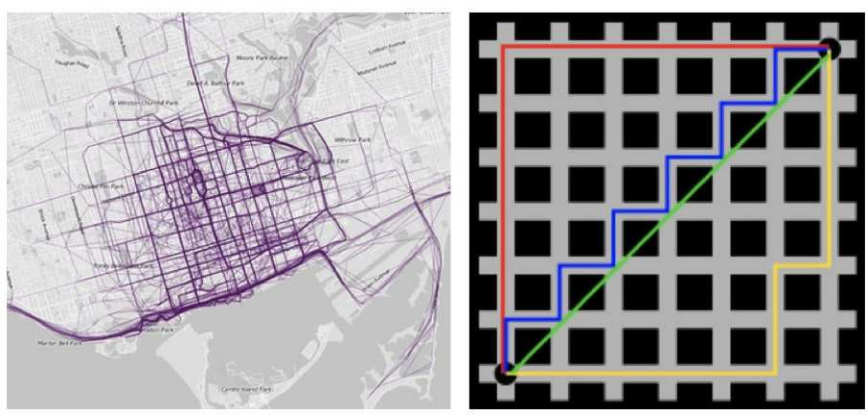
2.2曼哈顿距离(Manhattan Distance)****:
在曼哈顿街区要从⼀个⼗字路⼝开⻋到另⼀个⼗字路⼝,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是
"曼哈顿距离"。曼哈顿距离也称为"城市街区距离"(City Block distance)。
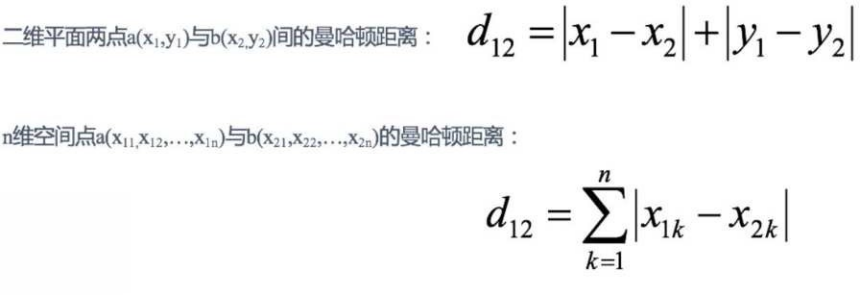
举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 2 4 6 2 4 2
2.3切⽐雪夫距离(Chebyshev Distance)****:
国际象棋中,国王可以直⾏、横⾏、斜⾏,所以国王⾛⼀步可以移动到相邻8个⽅格中的任意⼀个。国王从格⼦(x1,y1)
⾛到格⼦(x2,y2)最少需要多少步?这个距离就叫切⽐雪夫距离。
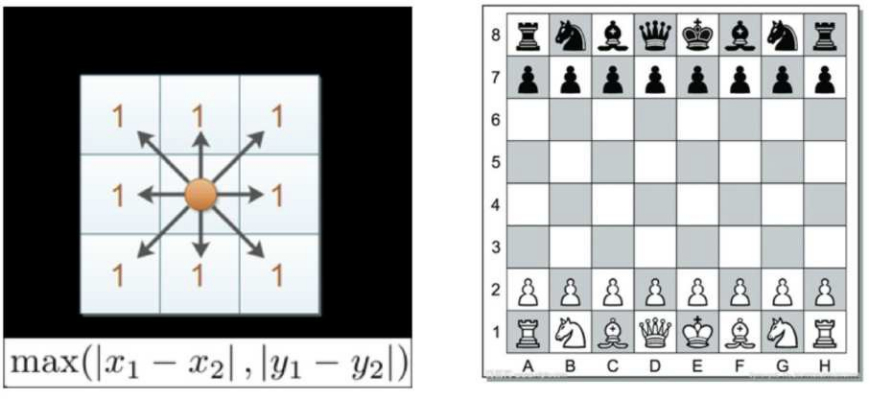
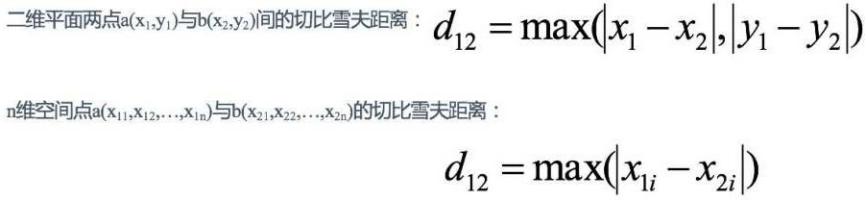
14距离度量
举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1 2 3 1 2 1
2.4闵可夫斯基距离(Minkowski Distance)****:
闵⽒距离不是⼀种距离,⽽是⼀组距离的定义,是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,...,x1n)与b(x21,x22,...,x2n)间的闵可夫斯基距离定义为:
其中p是⼀个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧⽒距离;
当p→∞时,就是切⽐雪夫距离。
15根据p的不同,闵⽒距离可以表示某⼀类/种的距离。
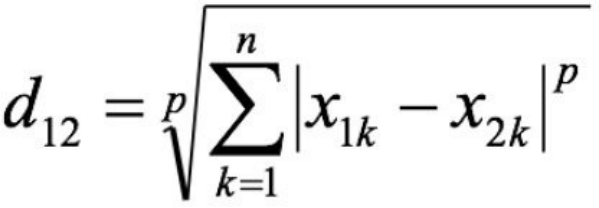
⼩结:
1 闵⽒距离,包括曼哈顿距离、欧⽒距离和切⽐雪夫距离,都存在明显的缺点:
e.g. ⼆维样本(身⾼[单位:cm],体重[单位:kg]),现有三个样本:a(180,50),b(190,50),c(180,60)。
a与b的闵⽒距离(⽆论是曼哈顿距离、欧⽒距离或切⽐雪夫距离)等于a与c的闵⽒距离。但实际上身⾼的10cm并不能
和体重的10kg划等号。
2****闵⽒距离的缺点:
(1)将各个分量的量纲(scale),也就是"单位"相同的看待了;
**(2)**未考虑各个分量的分布(期望,⽅差等)可能是不同的。
【拓展】其他距离公式
3 "连续属性"和"离散属性"的距离计算
我们常将属性划分为"连续属性" (continuous attribute)和"离散属性" (categorical attribute),前者在定义域上有⽆穷多个
可能的取值,后者在定义域上是有限个取值.
若属性值之间存在序关系,则可以将其转化为连续值,例如:身⾼属性"⾼""中等""矮",可转化为{1, 0.5, 0}。
闵可夫斯基距离可以⽤于有序属性。
若属性值之间不存在序关系,则通常将其转化为向量的形式,例如:性别属性"男""⼥",可转化为{(1,0),
(0,1)}。
4⼩结
1 距离公式的基本性质:⾮负性、统⼀性、对称性、直递性【了解】
2 常⻅距离公式
2.1 欧式距离(Euclidean Distance)【知道】:
通过距离平⽅值进⾏计算
2.曼哈顿距离(Manhattan Distance)【知道】:
通过距离的绝对值进⾏计算
3.切⽐雪夫距离 (Chebyshev Distance)【知道】:
维度的最⼤值进⾏计算
4.闵可夫斯基距离(Minkowski Distance)【知道】:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧⽒距离;
当p→∞时,就是切⽐雪夫距离。
3 属性【知道】
连续属性
离散属性,
存在序关系,可以将其转化为连续值
不存在序关系,通常将其转化为向量的形式