写在开头的话
学习了昨天的top k问题,今天让我们一起学习分治算法吧
第一节
知识点:
(1)分治思想(2)递归思想(3)汉诺塔问题
分治思想
简单介绍
分治思想是一种重要的问题解决方法,它将一个复杂的问题分解成多个相似的子问题来解决,然后将这些子问题的解合并起来得到原问题的解。这个过程包括三个主要步骤:分解、解决和合并。
分解:将原始问题划分成若干个规模较小的子问题。这一步骤需要考虑如何将问题划分为相互独立、互不重叠的子问题,通常通过递归的方式实现。每个子问题的规模都比原问题小,但是解决它们的方法与解决原问题的方法相同。
解决:通过递归地解决每个子问题,直到子问题的规模足够小,可以直接求解。
合并:将子问题的解合并成原始问题的解。这一步通常是最简单的,只需将各个子问题的解按照一定规则合并即可。
图示
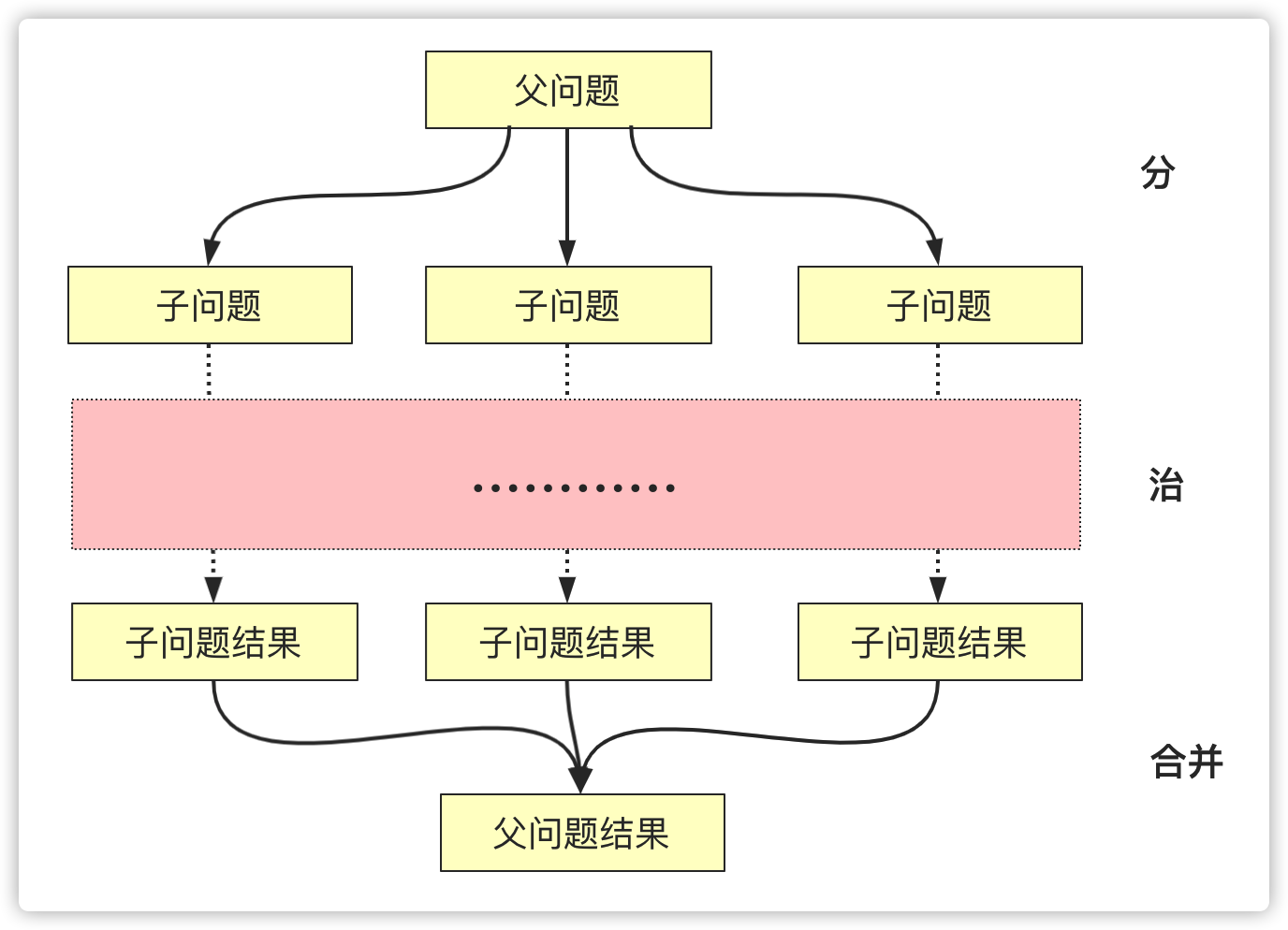
分治思想的应用
归并排序:归并排序是分治思想的一个典型应用。它将一个数组划分成两个规模相等的子数组,分别对这两个子数组进行归并排序,然后将排好序的子数组合并成一个有序数组。归并排序的时间复杂度为 O(nlogn)。
快速排序:快速排序也是分治思想的一种应用,它通过选择一个基准元素将数组分割成两个子数组,然后递归地对子数组进行排序。快速排序的时间复杂度也为 O(nlogn)。
二分查找:二分查找是一种分治思想的典型应用,它通过将查找范围分成两部分,然后确定目标值在哪一部分,从而将查找范围缩小一半。这种方法的时间复杂度为 O(logn)。是非常常用的查找技巧。
递归思想
简单介绍
递归思想是一种解决问题的方法,它将问题分解为规模更小的相似子问题,并通过不断调用自身来解决这些子问题。递归通常包含两个部分:基本情况和递归步骤。基本情况是指能够直接求解的最简单情况,递归步骤则是指将问题分解为更小规模的子问题。
递归的两个组成部分
基本情况(Base Case):递归算法必须包含一个或多个基本情况,这些情况不需要再次递归调用就可以直接求解。基本情况通常是递归函数停止递归的条件,它们防止递归无限进行下去,确保算法能够结束。
递归步骤(Recursive Step):递归算法通过调用自身来解决规模更小的子问题。在每次递归调用中,问题的规模都会减小,直到达到基本情况,然后开始回溯(即从递归调用中返回)。
汉诺塔问题
让我们通过汉诺塔问题详细介绍分治思想和递归思想的应用。
问题描述
汉诺塔问题是计算机科学中经典的递归问题之一。问题描述如下:假设有三根柱子(分别记为A、B、C),A柱子上有 n 个不同大小的圆盘,按照从小到大的顺序堆叠。要求将这些圆盘从A柱子移动到C柱子,并保持它们的顺序不变,同时不能跨越柱子移动,所以需要借助B柱子作为中转。在移动过程中,要求任意时刻大圆盘在下,小圆盘在上。
代码实现
C++代码实现
cpp
#include <iostream>
using namespace std;
void moveDisk(int n, char source, char dest, char aux) {
if (n == 1) {
cout << "Move disk 1 from " << source << " to " << dest << endl;
return;
}
moveDisk(n - 1, source, aux, dest);
cout << "Move disk " << n << " from " << source << " to " << dest << endl;
moveDisk(n - 1, aux, dest, source);
}
void hanoi(int n, char source, char dest, char aux) {
moveDisk(n, source, dest, aux);
}
int main() {
int n = 3; // 例如,移动3个圆盘
hanoi(n, 'A', 'C', 'B');
return 0;
}Java代码实现
java
public class HanoiTower {
public static void moveDisk(int n, char source, char dest, char aux) {
if (n == 1) {
System.out.println("Move disk 1 from " + source + " to " + dest);
return;
}
moveDisk(n - 1, source, aux, dest);
System.out.println("Move disk " + n + " from " + source + " to " + dest);
moveDisk(n - 1, aux, dest, source);
}
public static void hanoi(int n, char source, char dest, char aux) {
moveDisk(n, source, dest, aux);
}
public static void main(String[] args) {
int n = 3; // 例如,移动3个圆盘
hanoi(n, 'A', 'C', 'B');
}
}Python代码实现
python
def move_disk(n, source, dest, aux):
if n == 1:
print("Move disk 1 from", source, "to", dest)
return
move_disk(n - 1, source, aux, dest)
print("Move disk", n, "from", source, "to", dest)
move_disk(n - 1, aux, dest, source)
def hanoi(n, source, dest, aux):
move_disk(n, source, dest, aux)
if __name__ == "__main__":
n = 3 # 例如,移动3个圆盘
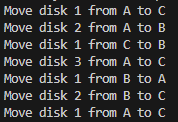
hanoi(n, 'A', 'C', 'B')运行结果
简单总结
本节详细了解了下分治思想和递归思想,并通过汉诺塔问题应用了展示了以上的思想应该如何应用。
第二节
知识点:
(1)传统乘法(2)分治法优化
传统乘法
具体步骤
传统乘法的原理基于逐位相乘和累加的过程。具体步骤如下:
-
逐位相乘:将一个数的每一位分别与另一个数的每一位相乘,得到若干个部分积(partial products)。每个部分积相当于一个数乘以另一个数的一位(并考虑其权重,即位数)。
-
累加部分积:将所有部分积按照其对应的位数进行累加。部分积的结果按照它们的位数进行排列和相加。
例子:123×45
1 2 3
× 4 5
_______
6 1 5 (123 × 5)
+ 4 9 2 0 (123 × 40, 因为是乘以4,并且要向左移一位)
_______
5 5 3 5详细步骤:
-
逐位相乘:
- 首先,取45的个位数5,与123的每一位相乘:123×5=615
- 然后,取45的十位数4(相当于40),与123的每一位相乘: 123×40=4920
-
累加部分积:
- 将两个部分积615和4920按照它们的位数对齐,然后相加
传统乘法的复杂度为O(),其中n是数字的位数。这是因为每一位的乘法操作需要与另一数的每一位进行相乘,并最终累加所有部分积。
尽管传统乘法方法简单且易于理解,但在处理大数时效率较低,因为操作次数随着数字位数的平方增长。因此,为了提高效率,在实际应用中往往需要更复杂的优化算法。
代码实现
C++代码实现
cpp
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
string multiply(string num1, string num2) {
int m = num1.size(), n = num2.size();
vector<int> result(m + n, 0);
for (int i = m - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
int mul = (num1[i] - '0') * (num2[j] - '0');
int p1 = i + j, p2 = i + j + 1;
int sum = mul + result[p2];
result[p1] += sum / 10;
result[p2] = sum % 10;
}
}
string res;
for (int num : result) {
if (!(res.empty() && num == 0)) {
res.push_back(num + '0');
}
}
return res.empty() ? "0" : res;
}
int main() {
string num1 = "123";
string num2 = "45";
cout << "C++ Result: " << multiply(num1, num2) << endl;
return 0;
}Java代码实现
java
public class MultiplyStrings {
public static String multiply(String num1, String num2) {
int m = num1.length(), n = num2.length();
int[] result = new int[m + n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
int p1 = i + j, p2 = i + j + 1;
int sum = mul + result[p2];
result[p1] += sum / 10;
result[p2] = sum % 10;
}
}
StringBuilder sb = new StringBuilder();
for (int num : result) {
if (!(sb.length() == 0 && num == 0)) {
sb.append(num);
}
}
return sb.length() == 0 ? "0" : sb.toString();
}
public static void main(String[] args) {
String num1 = "123";
String num2 = "45";
System.out.println("Java Result: " + multiply(num1, num2));
}
}Python代码实现
python
def multiply(num1, num2):
m, n = len(num1), len(num2)
result = [0] * (m + n)
for i in range(m - 1, -1, -1):
for j in range(n - 1, -1, -1):
mul = int(num1[i]) * int(num2[j])
p1, p2 = i + j, i + j + 1
sum = mul + result[p2]
result[p1] += sum // 10
result[p2] = sum % 10
result_str = ''.join(map(str, result))
return result_str.lstrip('0') or '0'
# Test
num1 = "123"
num2 = "45"
print(f"Python Result: {multiply(num1, num2)}")运行结果(呈现C++的结果)

分治法优化
卡拉茨巴算法(Karatsuba Algorithm)是一种用于大整数乘法的快速算法。它通过将乘法分解为多个较小的子问题来减少总的乘法运算次数。其时间复杂度为,比传统的竖式乘法的O(
)复杂度要高效得多。
算法原理
卡拉茨巴算法的基本思想是分治法,将两个大数分解成较小的部分,从而减少乘法运算的次数。
假设有两个 n 位数X和Y,我们将它们表示为:
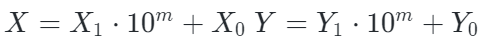
其中X1和Y1是高位部分,X0和Y0是低位部分,m是位数的一半。
根据上述表示法,乘积X×Y可以写成:
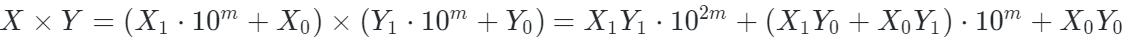
减少乘法次数
为了减少乘法运算次数,我们引入中间变量:
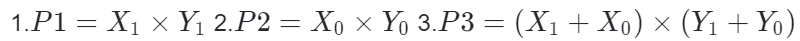
注意到P3可以展开为:
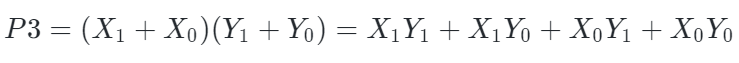
于是我们有:
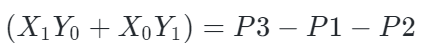
最终,乘积X×Y可以表示为:
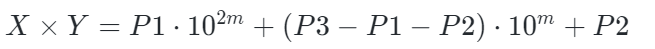
通过这种方式,我们将原来的四次乘法(传统竖式乘法)减少为三次乘法(卡拉茨巴算法),从而提高了计算效率。
递归实现
卡拉茨巴算法通常采用递归方式实现。对于每一层递归,我们都将问题分解成更小的子问题,直到子问题足够小,可以直接用简单的乘法解决。
示例
让我们通过一个具体的例子来理解卡拉茨巴算法。
假设我们要计算 1234×5678:
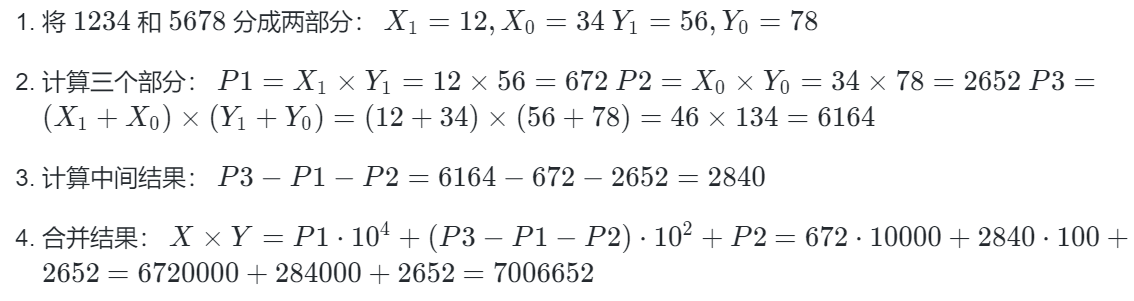
因此,1234×5678=7006652。
卡拉茨巴算法通过减少乘法次数来提高大数乘法的计算效率,特别适合大数的乘法运算。它的递归思想和分治法使得其在处理大数乘法时比传统方法更高效。
代码实现
C++代码实现
cpp
#include <bits/stdc++.h>
// Pad the string with zeros on the left to make its length equal to 'length'
std::string padZero(const std::string &str, int length) {
std::string result = str;
while (result.length() < length) {
result = "0" + result;
}
return result;
}
// Karatsuba algorithm for multiplying two large numbers represented as strings
std::string karatsuba(const std::string &x, const std::string &y) {
int n = std::max(x.size(), y.size());
if (n == 1) {
return std::to_string((x[0] - '0') * (y[0] - '0'));
}
if (n % 2 != 0) {
n++;
}
std::string xPadded = padZero(x, n);
std::string yPadded = padZero(y, n);
int m = n / 2;
std::string x1 = xPadded.substr(0, m);
std::string x0 = xPadded.substr(m, n - m);
std::string y1 = yPadded.substr(0, m);
std::string y0 = yPadded.substr(m, n - m);
std::string P1 = karatsuba(x1, y1);
std::string P2 = karatsuba(x0, y0);
std::string P3 = karatsuba(std::to_string(std::stoi(x1) + std::stoi(x0)), std::to_string(std::stoi(y1) + std::stoi(y0)));
int P1Int = std::stoi(P1);
int P2Int = std::stoi(P2);
int P3Int = std::stoi(P3);
int P3MinusP1MinusP2 = P3Int - P1Int - P2Int;
std::string result = std::to_string(P1Int * pow(10, n) + P3MinusP1MinusP2 * pow(10, m) + P2Int);
return result;
}
int main() {
std::string x = "1234";
std::string y = "5678";
std::string result = karatsuba(x, y);
std::cout << "Product: " << result << std::endl;
return 0;
}Java代码实现
java
public class Karatsuba {
public static String padZero(String str, int length) {
StringBuilder result = new StringBuilder(str);
while (result.length() < length) {
result.insert(0, "0");
}
return result.toString();
}
public static String karatsuba(String x, String y) {
int n = Math.max(x.length(), y.length());
if (n == 1) {
return Integer.toString((x.charAt(0) - '0') * (y.charAt(0) - '0'));
}
if (n % 2 != 0) {
n++;
}
x = padZero(x, n);
y = padZero(y, n);
int m = n / 2;
String x1 = x.substring(0, m);
String x0 = x.substring(m);
String y1 = y.substring(0, m);
String y0 = y.substring(m);
String P1 = karatsuba(x1, y1);
String P2 = karatsuba(x0, y0);
String P3 = karatsuba(Integer.toString(Integer.parseInt(x1) + Integer.parseInt(x0)), Integer.toString(Integer.parseInt(y1) + Integer.parseInt(y0)));
int P1Int = Integer.parseInt(P1);
int P2Int = Integer.parseInt(P2);
int P3Int = Integer.parseInt(P3);
int P3MinusP1MinusP2 = P3Int - P1Int - P2Int;
return Integer.toString(P1Int * (int)Math.pow(10, n) + P3MinusP1MinusP2 * (int)Math.pow(10, m) + P2Int);
}
public static void main(String[] args) {
String x = "1234";
String y = "5678";
String result = karatsuba(x, y);
System.out.println("Product: " + result);
}
}Python代码实现
python
def pad_zero(s, length):
return s.zfill(length)
def karatsuba(x, y):
n = max(len(x), len(y))
if n == 1:
return str(int(x) * int(y))
if n % 2 != 0:
n += 1
x = pad_zero(x, n)
y = pad_zero(y, n)
m = n // 2
x1, x0 = x[:m], x[m:]
y1, y0 = y[:m], y[m:]
P1 = karatsuba(x1, y1)
P2 = karatsuba(x0, y0)
P3 = karatsuba(str(int(x1) + int(x0)), str(int(y1) + int(y0)))
P1Int = int(P1)
P2Int = int(P2)
P3Int = int(P3)
P3MinusP1MinusP2 = P3Int - P1Int - P2Int
result = P1Int * 10**n + P3MinusP1MinusP2 * 10**m + P2Int
return str(result)
if __name__ == "__main__":
x = "1234"
y = "5678"
result = karatsuba(x, y)
print("Product:", result)运行结果

简单总结
本节主要学习了大数乘法,以及分治法优化大数乘法。