AR-Align-NN-2024 - 技术栈

文章目录

[An unsupervised multi-view contrastive learning framework with attention-based reranking strategy for entity alignment](#An unsupervised multi-view contrastive learning framework with attention-based reranking strategy for entity alignment)
- 摘要
- [1. 引言](#1. 引言)
- [2. 相关工作](#2. 相关工作)
- - [2.1. 实体对齐](#2.1. 实体对齐)
  - [2.2 对比学习中的数据增强](#2.2 对比学习中的数据增强)
- [3. 问题定义](#3. 问题定义)
- [4. 方法论](#4. 方法论)
- - [4.1 嵌入初始化](#4.1 嵌入初始化)
  - [4.2 图谱数据增强](#4.2 图谱数据增强)
  - [4.3 多视图对比学习](#4.3 多视图对比学习)
  - [4.4. 基于注意力的重排序](#4.4. 基于注意力的重排序)
  - [4.5 多任务学习](#4.5 多任务学习)
- [5 实验](#5 实验)
- - [5.1 性能对比](#5.1 性能对比)
  - [5.2. 消融实验](#5.2. 消融实验)
  - [5.3. 深入分析](#5.3. 深入分析)
- [6. 结论](#6. 结论)

本文是对原论文学习过程中的中文翻译，仅用于学术交流与科普分享，无任何商业目的。

翻译已尽力忠实原文，但受限于译者水平，可能存在偏差；术语或公式若有疑义，请以原文为准。

若原作者、期刊或版权方提出异议，译者将在收到通知后 24 小时内删除本文并致歉。

欢迎读者引用原文，并请注明出处

An unsupervised multi-view contrastive learning framework with attention-based reranking strategy for entity alignment

基于注意力重排序策略的无监督多视角对比学习实体对齐框架

AR-Align-NN-2024

摘要

实体对齐是知识图谱中的关键任务，旨在匹配不同知识图谱中的对应实体。由于现实场景中预对齐实体的稀缺性，无监督实体对齐研究日益受到关注。然而现有方法缺乏信息性实体引导，难以准确预测名称和结构相似的挑战性实体。为此，我们提出AR-Align框架------一种融合注意力重排序策略的无监督多视角对比学习方法。该框架采用两种数据增强技术分别生成邻域和属性的互补视图，通过多视角对比学习缩小增强实体间的语义鸿沟，并创新性地通过计算不同结构上的嵌入相似度加权和，对困难实体进行注意力重排序。实验表明，AR-Align在三个基准数据集上超越了多数有监督和无监督的先进方法。

1. 引言

知名大规模知识图谱（KGs），如YAGO和Wikidata，已支撑了诸多下游应用，包括推荐系统、问答平台以及复杂逻辑推理任务。由于来自不同源知识图谱的实体可能以不同名称表示，整合这些知识图谱面临重大挑战。为缓解此问题，实体对齐（EA）已成为关键研究领域，促进大规模知识图谱间的高效协作。

当前EA计算方法通常分为监督与无监督方法。监督EA可进一步分为基于翻译的方法和基于图神经网络的方法。然而，预对齐实体的固有稀缺性导致监督EA难以适应广泛现实场景，这促使无监督EA日益突出。先前无监督EA方法通常采用优化问题转换、伪标签生成和自监督学习来规避对标注数据的需求。

这些监督与无监督EA方法虽取得显著成功，但仍受困于"困难实体"问题------具有相似名称和结构的不同实体易被误对齐。例如，若负样本与目标实体过于相似，目标实体可能在候选实体中仅排名第二。对比学习中的困难负采样研究表明，选择高相似度负样本可有效增强嵌入的判别性。类似地，监督EA方法采用k近邻采样技术选择负样本，但该技术需标注数据以避免假阴性，使其在无监督场景中难以实施。现有无监督EA方法主要关注无标签下的性能提升，常忽视困难实体问题。UPLR和EVA基于语义或视觉相似度的高阈值标准生成伪标签，虽降低数据噪声，却易产生过于简单的标签，限制模型识别高相似度不同实体的能力。SelfKG和ICLEA通过负样本队列增加负样本数量，但队列中添加的数据批次经随机打乱，导致许多负样本与锚点实体差异显著。此类易区分负样本对模型助益有限。此外，SelfKG和ICLEA受限于单视角样本，使模型难以学习实体间的细微差异。

基于上述考量，我们提出了一种名为AR-Align的无监督多视角对比学习框架，该框架采用基于注意力的重排序策略来实现实体对齐。为突破现有局限，我们设计了基于注意力的重排序策略以挖掘困难实体。根据注意力分数，每个候选实体的不同嵌入相似度会自动获得相应权重。这种自适应方法的优势在于能根据数据特征和top-k排序评估候选实体嵌入的重要性，无需人工干预。随后通过嵌入相似度的加权和对候选实体重新排序。此外，采用混合操作来避免假阴性样本。基于注意力的重排序策略使模型能够通过重排序实体中的困难正样本和困难负样本来修正错误，从而学习更具判别性的特征。进一步地，我们引入了多视角对比学习框架：通过随机掩码邻居特征和自适应扰动属性特征生成两个增强视图，为实体提供互补信息；采用多视角对比损失函数来最小化增强实体在不同视角下的语义差距。本文主要贡献可概括为：

提出两种图数据增强方法（邻居特征掩码与自适应属性扰动）以提供互补信息
引入多视角对比学习方法以最小化增强实体跨视角的语义差距
开发基于注意力的重排序策略挖掘困难实体，使模型能区分相似实体的细微差异
通过在三个基准数据集上与有监督/无监督前沿方法的对比实验，验证了AR-Align的有效性

2. 相关工作

2.1. 实体对齐

实体对齐是知识图谱研究中的关键任务，旨在匹配不同知识图谱中的相同实体。为此已涌现大量方法，主要分为监督式与无监督式两大方法论。Zhang、Trisedya、Li、Jiang和Qi（2022年）提供了全面综述与基准测试，系统探讨了知识图谱实体对齐的各种方法与技术。早期监督方法仅关注结构信息，基于翻译的方法如MTransE和BootEA采用TransE获取实体表征。基于图神经网络的RDGCN设计了关系感知图卷积网络来捕捉邻域结构。CAECGAT通过预对齐种子传播跨图谱信息，提出新型上下文对齐增强的跨图注意力网络。DuGa-DIT利用图谱内注意力和跨图谱注意力层动态捕获邻域及跨图谱对齐特征。RANM提出自适应邻域匹配策略。AliNet与RPR-RHGT均致力于最小化多跳邻居噪声。PEEA将位置信息融入表征学习以解决标注数据不足导致的性能瓶颈。FuAlign采用预训练模型初始化并引入基于可靠性的稳定匹配。但仅依赖结构信息获取嵌入表征存在局限。为丰富实体表征，GAEA融合关系信息与数据增强进行基于间隔的对齐学习。EMEA通过邻居映射提升模型兼容性。STEA利用实体间依赖关系降低自训练策略中的假阳性噪声。JAPE、GCN-Align、AttrGNN及MHNA则结合属性三元组------包含属性及属性值，提供更丰富的语义信息。实践证明整合多样化附加信息可显著提升模型性能。多模态模型MCLEA与MEAformer采用对比学习损失函数学习跨模态关系。此外，MEAformer运用元学习与Transformer层动态调整不同模态权重。

监督学习方法依赖于大量预对齐实体，这在实际应用中并不现实。因此，研究者们越来越关注无监督和自监督方法的探索。例如，MultiKE采用跨知识图谱推理方法来提升对齐性能；AttrE通过计算编辑距离实现半自动谓词对齐，该方法使模型具备统一的关系嵌入空间，支持结构与属性嵌入的联合学习。SEU和UDCEA分别将跨语言实体对齐问题转化为分配问题和二分图匹配问题，从而摆脱对监督标签的依赖。此外，EVA利用图像特征相似性生成高置信度伪标签，UPLR则通过非采样校准策略提升伪标签质量。上述基于伪标签的方法聚焦于提升置信度，却忽视了信息丰富性。对比学习近期被应用于实体对齐领域，其通过最小化正样本对距离、最大化负样本对距离来优化实体表征。具体而言，SelfKG和ICLEA采用对比学习与多重负样本队列捕获实体特征。随着大语言模型（LLM）的兴起，部分方法开始运用ChatGPT和BLOOM等模型辅助实体对齐。AutoAlign在LLM支持下构建谓词邻近图，扩展了AttrE的功能，实现了知识图谱的自动对齐。

2.2 对比学习中的数据增强

数据增强在对比学习中至关重要，其通过对图结构进行扰动生成两个差异化视图以构成正样本对。为提升图表示学习效果，现有多种成熟的数据增强方法。例如GraphCL设计了节点丢弃、边扰动、属性掩码和子图抽取四类图增强策略；GCA提出自适应增强方法引导模型忽略不重要边上的噪声；SAIL通过自增强图对比学习平滑图拓扑与节点特征所度量邻近性的差异。此外，部分数据增强方法融合对抗学习以增强图表示学习的鲁棒性。尽管众多图数据增强方法已取得显著成效，基于对比学习的实体对齐在图数据增强领域仍有待深入探索。

3. 问题定义

本研究探索无监督标签的实体对齐(EA)方法。我们将知识图谱(KG)定义为 G = { E , R , A , V , T A , T R } G = \left\{ {E,R,A,V,{T}{A},{T}{R}}\right\} G={E,R,A,V,TA,TR}，其中 E , R , A , V E,R,A,V E,R,A,V分别表示实体集、关系集、属性集和值集。 T A = {T}{A} = TA= { ( e , a , v ) ∣ e ∈ E , a ∈ A , v ∈ V } \{ \left( {e,a,v}\right) \mid e \in E,a \in A,v \in V\} {(e,a,v)∣e∈E,a∈A,v∈V}称为属性三元组， T R = { ( e , r , t ) ∣ e , t ∈ E , r ∈ R } {T}{R} = \{ \left( {e,r,t}\right) \mid e,t \in E,r \in R\} TR={(e,r,t)∣e,t∈E,r∈R}称为关系三元组。给定两个知识图谱 G s = { E , R , A , V , T A , T R } {G}{s} = \left\{ {E,R,A,V,{T}{A},{T}{R}}\right\} Gs={E,R,A,V,TA,TR}和 G t = {G}{t} = Gt= { E ′ , R ′ , A ′ , V ′ , T A ′ , T R ′ } \left\{ {{E}^{\prime },{R}^{\prime },{A}^{\prime },{V}^{\prime },{T}{A}^{\prime },{T}{R}^{\prime }}\right\} {E′,R′,A′,V′,TA′,TR′}，已对齐实体对的集合定义为 S = { ( e , e ′ ) ∣ e ∈ E , e ′ ∈ E ′ , e ↔ e ′ } S = \left\{ {\left( {e,{e}^{\prime }}\right) \mid e \in E,{e}^{\prime } \in {E}^{\prime },e \leftrightarrow {e}^{\prime }}\right\} S={(e,e′)∣e∈E,e′∈E′,e↔e′}，其中 ↔ \leftrightarrow ↔表示等价关系。实体对齐旨在精准识别等价实体。根据是否使用 S S S，这些对齐方法可分为监督式或无监督式。

4. 方法论

我们开发了AR-Align实体对齐框架，采用多视角对比学习机制和基于注意力的重排序策略。如图1所示，AR-Align包含五个组件：(1)嵌入初始化4.1：通过预训练语言模型LaBSE初始化实体名称和属性；(2)图谱数据增强4.2：分别通过邻居特征掩码和自适应属性扰动创建两种增强视图；(3)多视角对比学习4.3：新型对比学习缩小增强实体不同视图间的语义差距；(4)基于注意力的重排序4.4：利用嵌入相似度加权和挖掘困难实体的策略；(5)多任务学习4.5：多个损失函数联合优化查询编码器和注意力重排序模块参数。具体细节如下。

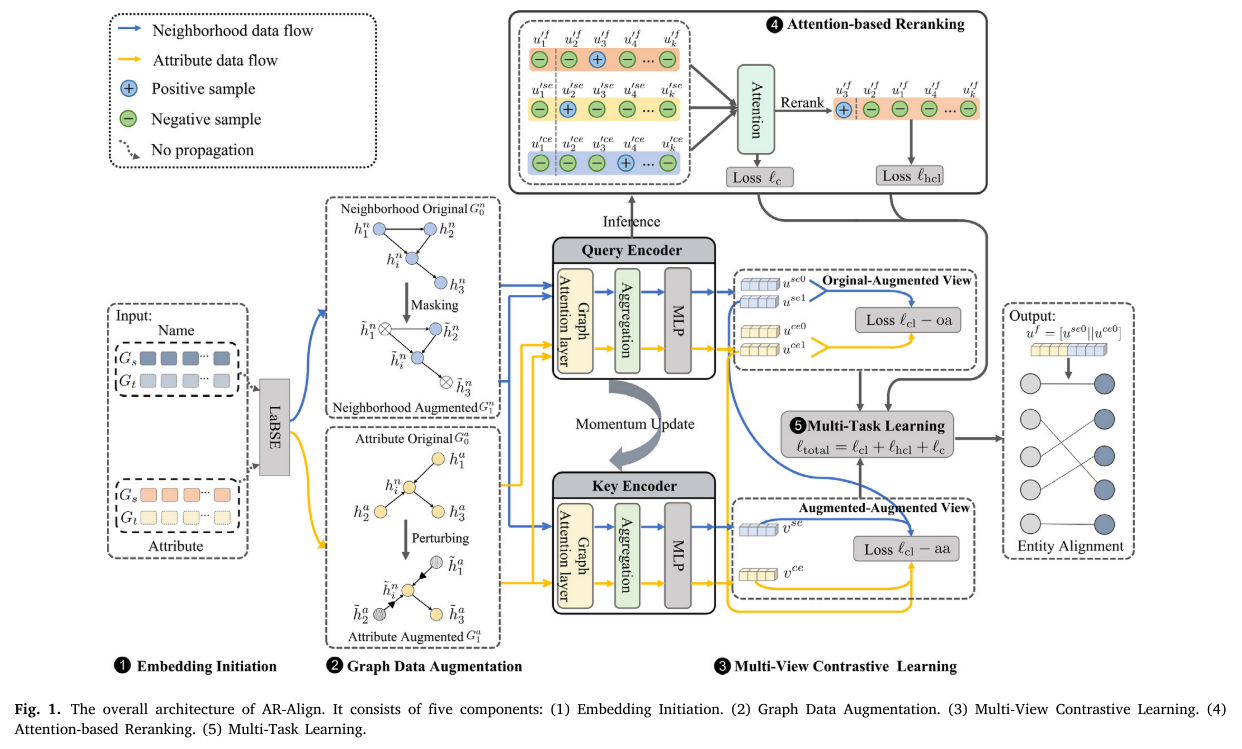
图1. AR-Align整体架构。包含五个组件：(1)嵌入初始化 (2)图数据增强 (3)多视图对比学习 (4)基于注意力的重排序 (5)多任务学习

4.1 嵌入初始化

使用多语言预训练语言模型进行嵌入初始化，可在无需额外翻译的情况下保留实体语义信息。因此引入多语言预训练模型初始化实体名称和属性如下：采用LaBSE------基于109种语言大规模语料训练的模型，提取实体名称 e n {e}^{n} en和属性 e a {e}^{a} ea的嵌入表示：

h n = ∥ f LaBSE ( e n ) ∥ 2 , (1) {h}^{n} = {\begin{Vmatrix}{f}{\text{LaBSE }}\left( {e}^{n}\right) \end{Vmatrix}}{2}, \tag{1} hn= fLaBSE (en) 2,(1)

h a = ∥ f LaBSE ( e a ) ∥ 2 , (2) {h}^{a} = {\begin{Vmatrix}{f}{\text{LaBSE }}\left( {e}^{a}\right) \end{Vmatrix}}{2}, \tag{2} ha= fLaBSE (ea) 2,(2)

其中 f LaBSE {f}{\text{LaBSE }} fLaBSE 为LaBSE编码器，直接用于初始化嵌入而无需微调。 ∥ ∥ 2 \parallel {\parallel }{2} ∥∥2表示 L 2 {L}_{2} L2范数运算。

4.2 图谱数据增强

图谱对比学习中的数据增强通过对输入图谱进行操作（如掩码、去噪、丢弃等）提供互补视图。为保留邻域结构和重要属性语义，我们开发了新型图谱数据增强方案，包含自适应扰动属性特征和掩码邻居特征。首先为实体 e . T R e.{T}{R} e.TR构建邻域子图和属性子图， T A {T}{A} TA分别表示关系三元组和属性三元组。在 T R {T}{R} TR中，头尾节点均为实体，边表示关系。为实体 e e e构建邻域子图时，我们采样其连接的一定数量实体作为邻居。在 T A {T}{A} TA中，头节点为实体，尾节点为属性值，边表示属性。由于属性值噪声较高，我们将其舍弃。此时将属性视为尾节点，采样实体 e e e连接的一定数量属性构建其属性子图。

邻居特征掩码。我们随机选择实体的邻居并将其所有特征置零。请注意，此操作保留了完整的拓扑结构而不移除任何边。给定实体 e e e在邻域子图中的邻居为 N e = {\mathcal{N}}{e} = Ne= { h 1 n , h 2 n , ... , h m n } \left\{ {{h}{1}^{n},{h}{2}^{n},\ldots ,{h}{m}^{n}}\right\} {h1n,h2n,...,hmn}，新生成的邻居特征 h ~ i n {\widetilde{h}}_{i}^{n} h in计算如下：

λ i n ∼ B ( 1 − p τ ) , ∀ i , {\lambda }{i}^{n} \sim \mathcal{B}\left( {1 - {p}{\tau }}\right) ,\forall i, λin∼B(1−pτ),∀i,

h ~ i n = { h i n λ i n = 1 0 λ i n = 0 , (3) {\widetilde{h}}{i}^{n} = \left\{ {\begin{array}{ll} {h}{i}^{n} & {\lambda }{i}^{n} = 1 \\ 0 & {\lambda }{i}^{n} = 0 \end{array},}\right. \tag{3} h in={hin0λin=1λin=0,(3)

其中 λ n ∈ R m × 1 {\lambda }^{n} \in {\mathbb{R}}^{m \times 1} λn∈Rm×1是从伯努利分布 B \mathcal{B} B采样的二元向量， p τ {p}_{\tau } pτ表示每个邻居特征被置零的概率。

自适应属性扰动。创建增强视图的过程通常会对实体的某些属性施加均匀扰动。然而这种方法可能破坏重要属性特征。我们认为保持重要属性的完整特征至关重要，而不重要属性可承受更广泛的扰动。受GCA中心性度量方法（Zhu等人，2021）启发，我们采用归一化的度中心性来评估给定属性 a i {a}_{i} ai的重要性：

c i = min ⁡ ( log ⁡ ( d max ⁡ − d i d max ⁡ − μ d ) ⋅ p γ , p γ ) , (4) {c}{i} = \min \left( {\log \left( \frac{{d}{\max } - {d}{i}}{{d}{\max } - {\mu }{d}}\right) \cdot {p}{\gamma },\;{p}_{\gamma }}\right) , \tag{4} ci=min(log(dmax−μddmax−di)⋅pγ,pγ),(4)

其中 d i {d}{i} di是属性 a i {a}{i} ai的总度数（根据包含 a i . d max ⁡ {a}{i}.{d}{\max } ai.dmax的属性三元组数量计算）， μ d {\mu }{d} μd和 d d d分别是 d d d的最大值与平均值。 p ν {p}{\nu } pν为扰动比率。给定属性子图中实体 e e e的属性为 N a = { h 1 a , h 2 a , ... , h m a } {\mathcal{N}}{a} = \left\{ {{h}{1}^{a},{h}{2}^{a},\ldots ,{h}{m}^{a}}\right\} Na={h1a,h2a,...,hma}，新生成的属性特征 h ~ i a {\widetilde{h}}_{i}^{a} h ia计算如下：

λ i a ∼ B ( 1 − c i ) , ∀ i , {\lambda }{i}^{a} \sim \mathcal{B}\left( {1 - {c}{i}}\right) ,\forall i, λia∼B(1−ci),∀i,

z i ∼ B ( 1 − p σ ) , ∀ i , (5) {z}{i} \sim \mathcal{B}\left( {1 - {p}{\sigma }}\right) ,\forall i, \tag{5} zi∼B(1−pσ),∀i,(5)

h ~ i a = { h i a λ i a = 1 h i a ⋅ z i ⊤ λ i a = 0 , {\widetilde{h}}{i}^{a} = \left\{ {\begin{array}{ll} {h}{i}^{a} & {\lambda }{i}^{a} = 1 \\ {h}{i}^{a} \cdot {z}{i}^{\top } & {\lambda }{i}^{a} = 0 \end{array},}\right. h ia={hiahia⋅zi⊤λia=1λia=0,

其中 λ a ∈ R m × 1 {\lambda }^{a} \in {\mathbb{R}}^{m \times 1} λa∈Rm×1是从伯努利分布 B \mathcal{B} B采样的二元向量， c i {c}{i} ci是每个属性被扰动的概率。 m m m为属性数量， f f f为特征维度。 z ∈ R m × f z \in {\mathbb{R}}^{m \times f} z∈Rm×f是从伯努利分布 B \mathcal{B} B采样的二元矩阵， p σ {p}{\sigma } pσ决定被置零的特征维度比例。

4.3 多视图对比学习

对比学习通过优化正负样本对之间的差异来提升性能。如图1所示，我们提出一种新型多视图对比学习方法，该方法整合了查询编码器和键编码器（各包含邻域聚合器和属性聚合器）。值得注意的是，键编码器的参数采用动量更新机制，并利用对比学习损失进行多视图优化。具体细节如下。

键编码器参数通过动量方式进行更新。此外，采用对比学习损失函数实现多视图优化。更多细节如下所述。

邻域聚合器。每个邻居实体的重要性各不相同。为捕获实体的邻域特征，我们采用GAT聚合中心节点相邻实体的嵌入表示，再通过全连接层将实体名称嵌入 h i n {h}{i}^{n} hin与邻域嵌入 h i s e {h}{i}^{se} hise相结合。最终邻域嵌入 u i s e {u}_{i}^{se} uise计算公式如下：

u i s e = W s [ h i n ∥ h i s e ] + b , {u}{i}^{se} = {W}{s}\left\lbrack {{h}{i}^{n}\parallel {h}{i}^{se}}\right\rbrack + b, uise=Ws[hin∥hise]+b,

h i s e = ∥ k = 1 K σ ( ∑ j ∈ N e α i j k W 1 k h ~ j n ) , (6) {h}{i}^{se} = {\parallel }{k = 1}^{K}\sigma \left( {\mathop{\sum }\limits_{{j \in {\mathcal{N}}{e}}}{\alpha }{ij}^{k}{W}{1}^{k}{\widetilde{h}}{j}^{n}}\right) , \tag{6} hise=∥k=1Kσ j∈Ne∑αijkW1kh jn ,(6)

α i j = e ( σ ( q ⊤ [ W 1 h ~ i n ∥ W 1 h ~ j n ] ) ) ∑ l ∈ N e e ( σ ( q ⊤ [ W 1 h ~ i n ∥ W 1 h ~ l n ] ) ) , {\alpha }{ij} = \frac{{e}^{\left( \sigma \left( {q}^{\top }\left\lbrack {W}{1}{\widetilde{h}}{i}^{n}\parallel {W}{1}{\widetilde{h}}{j}^{n}\right\rbrack \right) \right) }}{\mathop{\sum }\limits{{l \in {\mathcal{N}}{e}}}{e}^{\left( \sigma \left( {q}^{\top }\left\lbrack {W}{1}{\widetilde{h}}{i}^{n}\parallel {W}{1}{\widetilde{h}}_{l}^{n}\right\rbrack \right) \right) }}, αij=l∈Ne∑e(σ(q⊤[W1h in∥W1h ln]))e(σ(q⊤[W1h in∥W1h jn])),

其中 N e {\mathcal{N}}{e} Ne表示实体 e i . W s {e}{i}.{W}{s} ei.Ws的邻居集合， W 1 {W}{1} W1是全连接层的可学习权重矩阵， q q q是共享线性变换的权重矩阵， K K K是作为单层前馈神经网络实现的注意力机制。 σ \sigma σ表示多头注意力数量，代表LeakyReLU激活函数。

属性聚合器。在现实世界中，仅依赖实体的邻居特征是不够的，因为知识图谱常包含大量长尾实体，这会限制邻域信息的可用性。为丰富实体表征，我们使用图注意力网络(GAT)获取属性嵌入 h i c e {h}{i}^{ce} hice。类似地，通过全连接层将实体名称嵌入 h i n {h}{i}^{n} hin与属性嵌入 h i c e {h}{i}^{ce} hice结合，最终属性嵌入 u i c e {u}{i}^{ce} uice计算公式如下：

u i c e = W c [ h i n ∥ h i c e ] + b , {u}{i}^{ce} = {W}{c}\left\lbrack {{h}{i}^{n}\parallel {h}{i}^{ce}}\right\rbrack + b, uice=Wc[hin∥hice]+b,

h i c e = ∑ j ∈ N a σ ( β i j h ^ j a ) , {h}{i}^{ce} = \mathop{\sum }\limits{{j \in {\mathcal{N}}{a}}}\sigma \left( {{\beta }{ij}{\widehat{h}}_{j}^{a}}\right) , hice=j∈Na∑σ(βijh ja),

β i j = e ( σ ( h ^ j a ) ) ∑ l ∈ N a e ( σ ( h ^ l a ) ) , (7) {\beta }{ij} = \frac{{e}^{\left( \sigma \left( {\widehat{h}}{j}^{a}\right) \right) }}{\mathop{\sum }\limits_{{l \in {\mathcal{N}}{a}}}{e}^{\left( \sigma \left( {\widehat{h}}{l}^{a}\right) \right) }}, \tag{7} βij=l∈Na∑e(σ(h la))e(σ(h ja)),(7)

h ^ j a = W 2 h ~ j a , {\widehat{h}}{j}^{a} = {W}{2}{\widetilde{h}}_{j}^{a}, h ja=W2h ja,

其中 N a {\mathcal{N}}{a} Na表示实体属性集合， e i . W c {e}{i}.{W}{c} ei.Wc是全连接层的可学习权重矩阵， W 2 {W}{2} W2为共享线性变换的权重矩阵， σ \sigma σ代表LeakyReLU激活函数。最终通过拼接 u s e {u}^{se} use和 u c e {u}^{ce} uce得到实体融合嵌入 u f {u}^{f} uf。

动量更新。我们建立两个编码器：查询编码器与键编码器。查询编码器通过梯度反向传播在每次训练迭代中更新参数 θ q {\theta }{q} θq。而键编码器虽与查询编码器结构一致，但采用动量更新机制来维持负样本一致性，其参数 θ k {\theta }{k} θk更新方式如下：

θ k = δ × θ k + ( 1 − δ ) × θ q , δ ∈ [ 0 , 1 ) , (8) {\theta }{k} = \delta \times {\theta }{k} + \left( {1 - \delta }\right) \times {\theta }_{q},\delta \in \lbrack 0,1), \tag{8} θk=δ×θk+(1−δ)×θq,δ∈[0,1),(8)

其中 δ \delta δ为动量超参数。

对比学习。对比学习的优化目标是拉近正样本对距离、推远负样本对距离。给定正样本对时，负样本定义为除自身外的所有节点。这些负样本对可来自视图内和视图间实体，损失函数定义如下：

ℓ g c l = − log ⁡ e s ( u i , v i ) / τ e s ( u i , v i ) / τ + ∑ j = 1 , j ≠ i N e s ( u i , v j ) / τ + ∑ j = 1 , j ≠ i N e s ( u i , u j ) / τ , (9) \begin{array}{l} {\ell }{\mathrm{{gcl}}} = \\ \; - \log \frac{{e}^{s\left( {{u}{i},{v}{i}}\right) /\tau }}{{e}^{s\left( {{u}{i},{v}{i}}\right) /\tau } + \mathop{\sum }\limits{{j = 1,j \neq i}}^{N}{e}^{s\left( {{u}{i},{v}{j}}\right) /\tau } + \mathop{\sum }\limits_{{j = 1,j \neq i}}^{N}{e}^{s\left( {{u}{i},{u}{j}}\right) /\tau }}, \end{array} \tag{9} ℓgcl=−loges(ui,vi)/τ+j=1,j=i∑Nes(ui,vj)/τ+j=1,j=i∑Nes(ui,uj)/τes(ui,vi)/τ,(9)

式中 s ( u , v ) s\left( {u,v}\right) s(u,v)为计算相似度的点积操作， τ \tau τ是温度超参数。 u u u与 v v v分别代表查询编码器和键编码器的输出。

多对比视图。为减小实体不同视图间的语义差距，我们将原始视图纳入对比学习。具体将原始 G 0 n {G}{0}^{n} G0n和 G 0 a {G}{0}^{a} G0a经查询编码器处理得到原始视图 u s e 0 {u}^{se0} use0和 u c e 0 {u}^{ce0} uce0；增强后的 G 1 n {G}{1}^{n} G1n与 G 1 a {G}{1}^{a} G1a分别通过查询编码器和键编码器处理，获得增强视图 u s e 1 {u}^{se1} use1、 u c e 1 , v s e {u}^{ce1},{v}^{se} uce1,vse和 v c e {v}^{ce} vce。这两组视图配置如下：

原始-增强视图。 u s e 0 {u}^{se0} use0与 u s e 1 {u}^{se1} use1构成邻域原始-增强对， u c e 0 {u}^{ce0} uce0和 u c e 1 {u}^{ce1} uce1组成属性原始-增强对。原始视图与增强视图间的损失计算如下：

ℓ o a = ℓ g c l ( u s e 0 , u s e 1 ) + ℓ g c l ( u c e 0 , u c e 1 ) . (10) {\ell }{\mathrm{{oa}}} = {\ell }{\mathrm{{gcl}}}\left( {{u}^{se0},{u}^{se1}}\right) + {\ell }_{\mathrm{{gcl}}}\left( {{u}^{ce0},{u}^{ce1}}\right) . \tag{10} ℓoa=ℓgcl(use0,use1)+ℓgcl(uce0,uce1).(10)

增强-增强视图。将 u s e 1 {u}^{se1} use1和 v s e {v}^{se} vse视为邻域增强视图对， u c e 1 {u}^{ce1} uce1与 v c e {v}^{ce} vce作为属性增强视图对。两个增强视图间的损失计算如下：

ℓ a a = ℓ g c l ( u s e 1 , v s e ) + ℓ g c l ( u c e 1 , v c e ) . (11) {\ell }{\mathrm{{aa}}} = {\ell }{\mathrm{{gcl}}}\left( {{u}^{se1},{v}^{se}}\right) + {\ell }_{\mathrm{{gcl}}}\left( {{u}^{ce1},{v}^{ce}}\right) . \tag{11} ℓaa=ℓgcl(use1,vse)+ℓgcl(uce1,vce).(11)

最终，总对比学习损失 ℓ c l {\ell }_{\mathrm{{cl}}} ℓcl计算公式为：

ℓ c l = ℓ o a + ℓ a a . (12) {\ell }{\mathrm{{cl}}} = {\ell }{\mathrm{{oa}}} + {\ell }_{\mathrm{{aa}}}. \tag{12} ℓcl=ℓoa+ℓaa.(12)

4.4. 基于注意力的重排序

相比简单伪标签，困难实体能为模型训练提供更有价值的信息。但由于这些实体与邻近实体高度相似，模型可能难以将其排在候选集前列。如图1所示，我们提出基于注意力的重排序策略，通过计算不同结构上嵌入相似度的加权和来挖掘困难实体，具体细节如下。

给定源实体 e i {e}{i} ei，候选目标实体为 N e ′ = {\mathcal{N}}{{e}^{\prime }} = Ne′= { e 1 ′ , e 2 ′ , ... , e n ′ } \left\{ {{e}{1}^{\prime },{e}{2}^{\prime },\ldots ,{e}{n}^{\prime }}\right\} {e1′,e2′,...,en′}。每个目标实体包含来自查询编码器的三种嵌入： u ′ f , u ′ s e {u}^{\prime f},{u}^{\prime {se}} u′f,u′se、 u ′ c e {u}^{\prime {ce}} u′ce。各目标实体的新得分 r ( e k ′ ) r\left( {e}{k}^{\prime }\right) r(ek′)计算公式如下：

d ( u i x , u k ′ x ) = e w k x s ( u i x , u k ′ x ) ∑ j = 1 n e w j x s ( u i x , u j ′ x ) s ( u i x , u k ′ x ) , x ∈ M , (13) d\left( {{u}{i}^{x},{u}{k}^{\prime x}}\right) = \frac{{e}^{{w}{k}^{x}s\left( {{u}{i}^{x},{u}{k}^{\prime x}}\right) }}{\mathop{\sum }\limits{{j = 1}}^{n}{e}^{{w}{j}^{x}s\left( {{u}{i}^{x},{u}{j}^{\prime x}}\right) }}s\left( {{u}{i}^{x},{u}_{k}^{\prime x}}\right) ,\;x \in \mathcal{M}, \tag{13} d(uix,uk′x)=j=1∑newjxs(uix,uj′x)ewkxs(uix,uk′x)s(uix,uk′x),x∈M,(13)

r ( e k ′ ) = ∑ x ∈ M d ( u i x , u k ′ x ) , r\left( {e}{k}^{\prime }\right) = \mathop{\sum }\limits{{x \in \mathcal{M}}}d\left( {{u}{i}^{x},{u}{k}^{\prime x}}\right) , r(ek′)=x∈M∑d(uix,uk′x),

其中 w k x {w}{k}^{x} wkx为可学习的注意力权重， s ( u x , u ′ x ) s\left( {{u}^{x},{u}^{\prime x}}\right) s(ux,u′x)为计算相似度的点积操作， n n n表示候选目标实体数量。集合 M = { f , s e , c e } \mathcal{M} = \{ f,{se},{ce}\} M={f,se,ce}代表三类实体嵌入：邻域、属性和融合。集合 V e ′ = {\mathcal{V}}{{e}^{\prime }} = Ve′= { u 1 ′ + , u 2 ′ − , ... , u n ′ − } \left\{ {{u}{1}^{\prime + },{u}{2}^{\prime - },\ldots ,{u}{n}^{\prime - }}\right\} {u1′+,u2′−,...,un′−}按得分 r ( e k ′ ) r\left( {e}{k}^{\prime }\right) r(ek′)从高到低重排序， u 1 ′ + {u}_{1}^{\prime + } u1′+作为硬正样本，其余样本为硬负样本。为防止负样本集中的假阴性，采用混合操作计算如下：

mix ⁡ ( u j ′ − ) = ξ ⋅ u j ′ − + ( 1 − ξ ) u 1 ′ + , j ∈ [ 2 , n ] , (14) \operatorname{mix}\left( {u}{j}^{\prime - }\right) = \xi \cdot {u}{j}^{\prime - } + \left( {1 - \xi }\right) {u}_{1}^{\prime + },\;j \in \left\lbrack {2,n}\right\rbrack , \tag{14} mix(uj′−)=ξ⋅uj′−+(1−ξ)u1′+,j∈[2,n],(14)

其中 ξ \xi ξ为混合超参数。随后对重排序集 V e ′ {V}_{{e}^{\prime }} Ve′应用InfoNCE损失函数（Oord, Li,&Vinyals,2018）：

ℓ h c l = − log ⁡ e ( s ( u i , u 1 ′ + ) / τ ) ∑ k = 2 n e ( s ( u i , mix ⁡ ( u k ′ − ) ) / τ ) , (15) {\ell }{\mathrm{{hcl}}} = - \log \frac{{e}^{\left( s\left( {u}{i},{u}{1}^{\prime + }\right) /\tau \right) }}{\mathop{\sum }\limits{{k = 2}}^{n}{e}^{\left( s\left( {u}{i},\operatorname{mix}\left( {u}{k}^{\prime - }\right) \right) /\tau \right) }}, \tag{15} ℓhcl=−logk=2∑ne(s(ui,mix(uk′−))/τ)e(s(ui,u1′+)/τ),(15)

其中 τ \tau τ为温度超参数，与公式(9)定义相同。

鉴于实体 e k ′ {e}{k}^{\prime } ek′在候选集中的排名越高，其作为目标实体的可能性越大。通过均匀分布自动生成实体 e k ′ {e}{k}^{\prime } ek′的权重 w k x {w}_{k}^{x} wkx：

ℓ c = K L ( w x ∥ w t ) , (16) {\ell }_{\mathrm{c}} = \mathrm{{KL}}\left( {{w}^{x}\parallel {w}^{t}}\right) , \tag{16} ℓc=KL(wx∥wt),(16)

其中 w t {w}^{t} wt与 w x {w}^{x} wx维度相同，其值从均匀分布采样后按逆序排列。通过最小化 w t {w}^{t} wt与 w x {w}^{x} wx分布的KL散度，确保 w x {w}^{x} wx满足逆序约束。

4.5 多任务学习

无监督优化过程的总损失定义为 ℓ c l , ℓ h c l {\ell }{\mathrm{{cl}}},{\ell }{\mathrm{{hcl}}} ℓcl,ℓhcl与 ℓ c {\ell }_{\mathrm{c}} ℓc之和：

ℓ total = ℓ c l + ℓ h c l + ℓ c , (17) {\ell }{\text{total }} = {\ell }{\mathrm{{cl}}} + {\ell }{\mathrm{{hcl}}} + {\ell }{\mathrm{c}}, \tag{17} ℓtotal =ℓcl+ℓhcl+ℓc,(17)

总损失函数 ℓ total {\ell }_{\text{total }} ℓtotal 专为多任务学习设计，可同步优化查询编码器与基于注意力的重排序模块参数。

5 实验

数据集。采用WK31-15K、DBP15K和DWY100K三个基准数据集评估AR-Align效果。

WK31-15K 包含英法、英德两个跨语言数据集，各含V1和V2两个版本，其中V2比V1密度更高。
DBP15K 包含源自DBpedia的中英、日英、法英三个跨语言数据集。
DWY100K 包含DBP-WD和DBP-YG两个大规模单语数据集，每个知识图谱均含10万个对齐实体。

详细数据集统计信息见表1。

基线方法。我们将提出的方法与监督式和非监督式方法进行对比。对于监督式方法，为便于比较分析，将其分为两组：第一组仅使用结构信息，包括以下方法：MTransE、BootEA、RDGCN、AliNet、CAEC-GAT、DuGa-DIT、RPR-RHGT、PEEA、RANM以及FuAlign；第二组使用属性或关系信息作为输入，包括：JAPE、GCN-Align、MRAEA、AttrGNN、MHNA、EMEA、SDEA、STEA、GAEA、MCLEA和MEAformer。此外，还与MultiKE、AttrE、SEU、EVA、SelfKG、ICLEA、UPLR、UDCEA及AutoAlign等非监督方法进行了比较。

评估指标。与现有研究一致，采用Hit@ k ( k = 1 , 10 ) k\left( {k = 1,{10}}\right) k(k=1,10)和MRR（平均倒数排名）作为评估指标。Hit@k表示正确对齐实体位于前 k k k候选中的比例，MRR通过公式 1 N ∑ i = 1 N 1 rank ⁡ i \frac{1}{N}\mathop{\sum }\limits_{{i = 1}}^{N}\frac{1}{{\operatorname{rank}}_{i}} N1i=1∑Nranki1计算倒数排名的平均值（其中 N N N代表测试集样本量）。Hit@k与MRR值越高，表明性能越优。

表1 数据集统计。WK31-15K包含英语（EN）、法语（FR）和德语（DE）；DBP15K包含中文（ZH）、日语（JA）、法语（FR）和英语（EN）；DWY100K则涉及DBpedia、Wikidata和YAGO3。

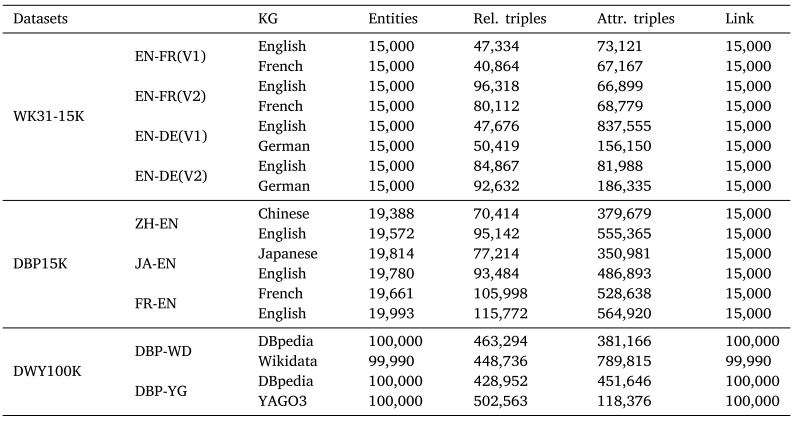
表2 DBP15K数据集上的实验结果。"#"表示使用预训练语言模型（如LaBSE）作为初始化方法的基线模型。" ⋆ \star ⋆"表示使用多模态信息的基线模型。加粗结果为各组别中的最佳结果。

实现细节。AR-Align采用Python和Pytorch框架实现，优化器选用Adam（学习率1e-4），在配备Intel E5-2680 CPU和GPU（3090/24G显存）的工作站上执行任务。整个实验过程中，输入嵌入维度、批大小、训练轮次、注意力头数、动量系数 δ \delta δ、温度参数 τ \tau τ、掩码率 p τ {p}{\tau } pτ、扰动率 p γ {p}{\gamma } pγ、维度比率 p σ {p}{\sigma } pσ及混合系数 ξ \xi ξ分别设置为768、512、300、1、0.9999、0.08、0.2、0.3、0.9和0.8。为公平对比，所有模型均未使用实体描述作为特征。预训练语言嵌入统一采用LaBSE（Feng等人，2022）初始化，且不涉及翻译过程。为高效评估AR-Align，我们使用相似性搜索工具Faiss 4 {}^{4} 4，基于 L 2 {L}{2} L2距离度量识别目标知识图谱中排名1-10的最近邻实体。实验中从训练集划分 5 % 5\% 5%作为验证集，验证集表现最佳的模型将用于测试集性能评估。AR-Align源代码及测试数据详见：https://github.com/edc3000/AR-Align。

表3 WK31-15K数据集结果。"#"标记表示使用预训练语言模型（如LaBSE）初始化的基线方法。加粗结果为各组最优值。

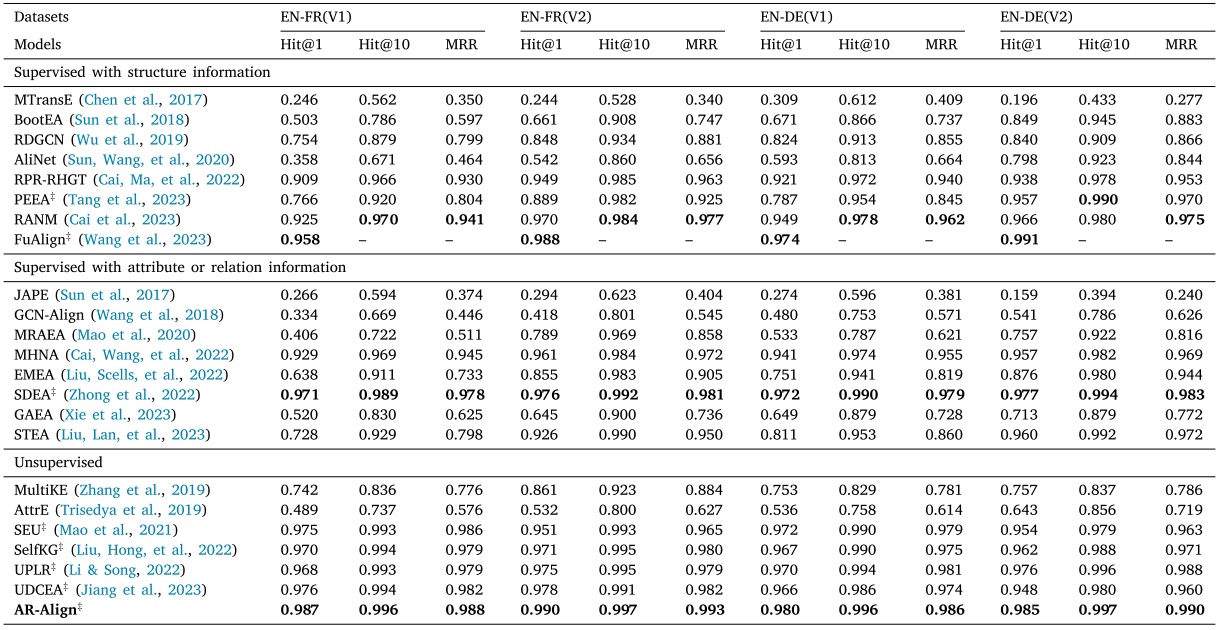
5.1 性能对比

表2、表3和表4展示了所有基线的性能表现

表4 DWY100K数据集结果。"#"标记表示使用预训练语言模型（如LaBSE）初始化的基线。加粗结果为各组最优值。

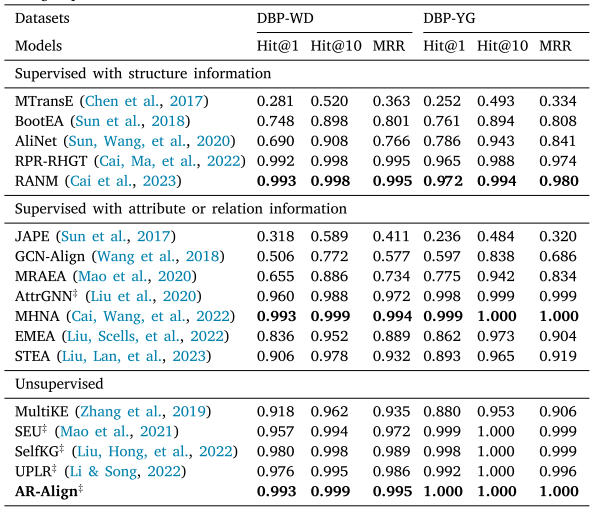
与无监督方法相比，我们的AR-Align模型在WK31-15K和DWY100K数据集上分别以0.8%-1.2%和0.1%-1.3%的hit@1指标优势超越次优方法。多模态方法MCLEA和MEAformer在DBP15K的中英（ZH-EN）和日英（JA-EN）语对上表现突出，这证明了多模态信息能有效帮助模型从不同信息视角区分实体。值得注意的是，AR-Align在中英和日英语对上的表现与这些方法相当，在DBP15K的法英（FR-EN）语对上甚至更优，这验证了我们提出的多视角对比学习和基于注意力的重排序策略的有效性与可比性。SelfKG和ICLEA均采用对比学习，其中ICLEA通过融入关系语义信息和伪对齐对来增强性能，但这些方法受限于单一视角对比。实验结果表明，AR-Align通过图数据增强实现了更全面的对比信息利用。EVA和UPLR分别基于视觉/语义相似度的高阈值标准生成伪标签，这类标签可能过于简单且缺乏辨别细微差异的指导信息。AR-Align在三个数据集上均超越UPLR，证明基于注意力的重排序策略能有效通过挖掘困难样本来提升性能。AttrE和AutoAlign因属性值噪声影响嵌入编码而表现欠佳，但AutoAlign借助ChatGPT和BLOOM等大语言模型实现全自动对齐，在日英语对上优于AttrE，这预示大语言模型为性能提升提供了新方向（如减少人工干预）。

在有监督方法组中，可划分为两类：利用结构信息的方法和利用附加信息（如关系与属性信息）的方法。我们观察到，附加信息类方法整体表现优于结构信息类。具体而言，多模态方法MEAformer和MCLEA超越了所有其他有监督方法，这归因于多模态方法能有效整合多种信息类型（如视觉、结构、关系和属性）。MEAformer采用元学习和Transformer层动态调整不同模态的权重，相比MCLEA取得了更优性能。虽然EVA也是多模态方法，但因缺乏监督标签和对比学习导致性能下降。值得注意的是，我们的AR-Align在DBP15K的FR-EN数据集上表现与MEAformer相当，这验证了多视角对比学习和基于注意力的重排序策略的有效性。CAECGAT和DuGa-DIT整合了跨知识图谱信息，其中DuGa-DIT通过动态更新新预测实体的注意力分数显著提升性能。PEEA和STEA都致力于解决标注数据不足问题，STEA还利用实体间依赖关系降低假阳性噪声。我们的AR-Align优于PEEA和STEA，证明了无监督框架和重排序策略的优势，使模型无需依赖标注数据。此外，通过基于多视角嵌入和top-k排序的重候选实体，该策略有效缓解了假阳性噪声。

我们进一步发现：(1) 采用LaBSE初始化的基线方法普遍优于其他初始化方法（如GloVe和fastText）；(2) LaBSE初始化的有监督方法整体超越使用LaBSE的无监督方法，例如FuAlign和SDEA显著优于所有LaBSE无监督方法；(3) 其他初始化的有监督方法通常优于采用其他方法的无监督方法，如MultiKE和EVA表现低于其他方法初始化的有监督基线；(4) 有趣的是，LaBSE初始化的无监督方法甚至优于其他初始化的有监督方法。最终如消融实验5.2所示，LaBSE被证明是最有效的初始化方法。

5.2. 消融实验

图数据增强、基于注意力的重排序策略、多视角对比学习和属性是AR-Align的核心组件。为验证各组件有效性，我们设计了消融实验，构建了AR-Align的七个变体：

w/o GDA：移除图数据增强（GDA）模块
w/o AR：移除基于注意力的重排序（AR）模块
w/ SV：排除多视角对比损失 ℓ o a {\ell }_{\mathrm{{oa}}} ℓoa，仅保留单视角对比学习
Arch. only：鉴于属性信息与重排序模块的关联性，同时移除两者并与w/o AR对比，以评估属性信息的重要性
w/ IL：用迭代学习（IL）替代AR模块，通过将模型预测作为伪标签进行连续训练，以评估AR的相对优势
w/ GloVe：采用GloVe词嵌入技术初始化实体嵌入，该技术通过共现矩阵和矩阵分解捕获词语义信息，作为LaBSE的替代方案
采用fastText：fastText是另一种词嵌入技术，它通过融合子词信息来增强词语表征。在本研究中，我们使用预训练的fastText向量初始化实体嵌入，而非LaBSE。

如表5所示，对比实验表明，未使用图数据增强（w/o GDA）时AR-Align的hit@1指标下降 0.8 % − 2.8 % {0.8}\% - {2.8}\% 0.8%−2.8%。这说明数据增强能通过多视角表征嵌入来提升模型鲁棒性。仅使用单一对比视角（w/ SV）时，hit@1下降约1%，证实多对比视角对弥合增强实体间语义鸿沟的重要性。值得注意的是，移除基于注意力的重排序（w/o AR）模块后，AR-Align性能显著下降，hit@1最大降幅达5%。而用迭代学习（w/ IL）替代AR模块时，hit@1下降约2%，凸显了我们AR模块的有效性。迭代学习使用模型预测作为伪标签，这些标签往往过于简单化，限制了模型指导效果。为解决此局限，AR模块通过计算嵌入相似度的加权和来挖掘困难实体，这些实体能帮助AR-Align更有效识别细微差异。当排除属性信息（标记为Arch. only）时，hit@1下降0.2%-6.8%，表明属性为实体表征学习提供了全面信息。这些结果证明，图数据增强、基于注意力的重排序策略、多对比视角和属性信息共同提升了AR-Align的性能。

表5 AR-Align组件的消融研究。GDA、AR、SV、Arch. only、IL、GloVe和fastText分别代表图数据增强(graph data augmentation)、基于注意力的重排序(attention-based reranking)、单一对比视图(single contrastive view)、仅结构(structure only)、迭代学习(iterative learning)、GloVe初始化和fastText初始化。

为探究初始化效果，我们进行实验：分别用GloVe和fastText替代LaBSE初始化实体表征。如表5所示，采用LaBSE的AR-Align显著优于GloVe和fastText变体。这验证了LaBSE的有效性------基于大规模多语料库训练且模型复杂度更高的LaBSE，能有效缩小跨语言语义鸿沟，使相似实体在嵌入空间中更紧密。

5.3. 深入分析

掩码与扰动比例的鲁棒性研究。我们对图数据增强的超参数进行敏感性分析，重点考察掩码比例 p τ {p}{\tau } pτ和扰动比例 p γ {p}{\gamma } pγ对鲁棒性的影响。将比例从0.0调整至0.5（零值表示禁用该操作），实验时固定其中一个参数。如图2(a)所示，图数据增强显著提升模型性能，且比例增大时性能保持稳定，表明AR-Align对图数据增强超参数不敏感，在参数调整中保持鲁棒性。

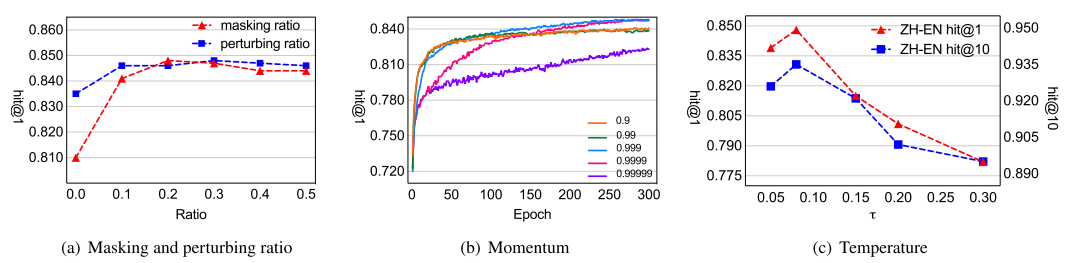
图2. 中英数据集上掩码比例、扰动比例、温度参数和动量参数的敏感性分析。

温度与动量的影响。温度参数 τ \tau τ和动量参数 δ \delta δ是多视角对比学习的核心超参数，其中动量值影响负样本一致性（He等人，2020）。如图2(b)所示，当动量 δ \delta δ处于0.999至0.9999区间时AR-Align表现良好，且不同动量值均能保持训练稳定性。最优温度参数可帮助模型隐式学习困难负样本（Chen等人，2020）。图2©显示，温度设为0.08左右时性能最佳。

在更具挑战性的数据集上评估。现实场景中的实体对齐(EA)因大量相似实体的存在而变得复杂。为模拟这种情况，我们创建了中英数据集(ZH-EN)的困难版本：首先通过名称嵌入计算已对齐实体与其前5个最近邻实体的平均相似度，按降序排列后，排名靠前的实体与其相邻实体间的高相似度显著增加了模型预测难度。据此我们选取前 50 % , 30 % {50}\% ,{30}\% 50%,30%和 10 % {10}\% 10%比例的实体构建困难版本，其中10%难度级别最具挑战性。如图3所示，所有基线模型的hit@1指标相对常规版本均下降，但AR-Align在所有难度级别上持续领先。这种优势源于我们的注意力重排序(AR)模块能有效区分困难实体。值得注意的是，UPLR和SelfKG在10%难度级别的hit@1显著下降，而AR-Align仍保持高效，凸显其在实际场景的适用性。与无 A R \mathrm{{AR}} AR和 w / I L \mathrm{w}/\mathrm{{IL}} w/IL的版本相比，性能差距随难度增加而扩大，分别达到2.7%-4.0%和6.7%-8.8%的差异，证实了AR模块的优越性。

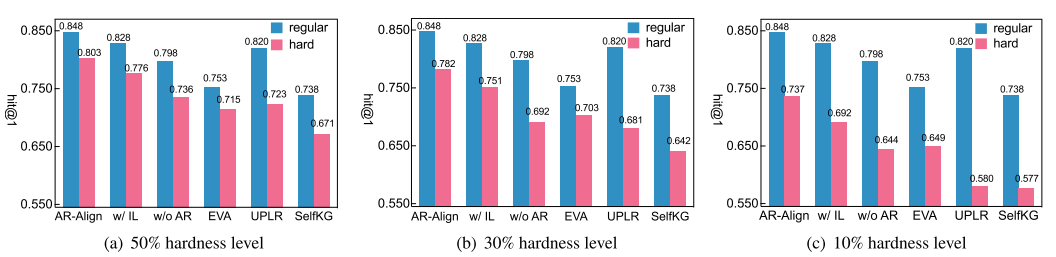
图3. 中英数据集上不同难度级别研究。

6. 结论

本文提出基于注意力重排序策略的无监督多视图对比学习框架AR-Align用于实体对齐。具体而言，输入数据通过图增强模块生成两种视图：邻域增强视图和属性增强视图。通过开发多视图对比学习机制来缩小增强实体的不同视图间的语义差距。此外，我们设计基于注意力的重排序策略，通过自动分配权重挖掘困难实体。最终通过优化总体损失获得实体嵌入向量。在三个基准数据集上的实验验证了AR-Align的有效性和泛化能力。

尽管AR-Align表现出色，仍有改进空间。与其他基于语义嵌入的实体对齐方法(Cai, Ma等, 2022; Liu等, 2020; Wang等, 2023; Zhong等, 2022)类似，AR-Align面临实体名称缺失的挑战。为提升普适性，我们计划开发灵活框架，在可获得时序数据时利用时间信息(Cai, Mao等, 2022; Liu, Wu, Li, Chen & Gao, 2023)补充缺失的实体名称。此外，将通过融合视觉信息(Chen等, 2023)增强实体嵌入的区分度。预期改进后的AR-Align将推动未来研究。