Shapley与SHAP - 技术栈

Shapley 值

Shapley值是SHAP（SHapley Additive exPlanations）图的核心理论基础。SHAP图通过可视化Shapley值来解释机器学习模型的预测结果。以下详细说明Shapley值与SHAP图之间的关系：

Shapley 值源于合作博弈理论，将机器学习模型中单个实例的预测视为 "总支出"，把实例的每个特征值看作 "玩家"，用于公平分配特征对预测的贡献。

其计算基于所有可能的特征联盟（特征组合），通过计算特征在不同联盟中的平均边际贡献来确定。边际贡献是指特征加入某一联盟后，联盟预测结果的变化。将这些边际贡献加权平均，便得到该特征的 Shapley 值。

Shapley 值具有效益性（所有特征贡献之和等于预测值与平均预测值的差值）、对称性（对所有联盟贡献相同的特征，其贡献值相同）、虚拟性（对任何联盟都无贡献的特征，其贡献值为 0）和可加性（组合游戏的 Shapley 值是各子游戏 Shapley 值之和）等良好性质。

从数学上看，特征j的 Shapley 值公式为：

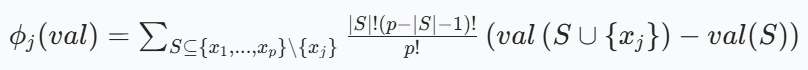
其中，S是不包含特征j的特征子集，(|S|)是子集S中特征的数量，p是特征的总数量，(val(S))是特征子集S的预测值（通过对未包含在S中的特征进行边缘化计算得到），(val(S +{x_j}))是加入特征j后联盟的预测值。

权重系数

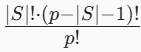
这个公式是 Shapley 值计算中用于确定 "权重" 的系数，其作用是对不同特征子集 S 的 "边际贡献" 进行加权平均，核心是为了体现 "公平性"，而不是直接算 "平均值"，但最终会通过加权平均得到每个特征的 Shapley 值。

下面展开解释它的含义和作用：

|S|：特征子集 S 的大小（即子集中包含的特征数量）。
p：模型的总特征数量（所有参与预测的特征总数）。
|S|!：子集 S 的 "排列数"（可以理解为子集内部特征的组合方式）。
(p - |S| - 1)!："剩余特征" 的排列数（除了子集 S 和当前关注的特征 j 之外，剩下特征的组合方式）。
p!：所有特征的总排列数（所有特征的组合方式总数）。

系数本质

Shapley 值的核心逻辑是 "公平分配" 特征对预测结果的贡献，需要考虑 "特征子集 S 出现的概率"。

从 "排列组合" 角度看：

总共有 p! 种方式排列所有特征，而包含 "子集 S、当前特征 j、剩余特征" 的排列方式可以拆成三部分：

子集 S 的排列：|S|! 种
当前特征 j 的固定位置：放在子集 S 之后（所以中间有一个 "固定步骤"）
剩余特征（除 S 和 j）的排列：(p - |S| - 1)! 种

因此，"包含子集 S 且当前特征 j 处于特定顺序" 的排列数 是 |S|! * 1 * (p - |S| - 1)!（"1" 是当前特征 j 的固定位置）。

从 "概率" 角度看：

这个系数本质是 "特征子集 S 出现的概率权重" ------ 它衡量了 "子集 S 作为当前特征 j 的 "前置条件" 时，在所有可能的特征组合中出现的 "公平占比"。

简单说：不同的子集 S 对特征 j 的 "边际贡献" 影响力不同，这个系数就是用来 "公平加权" 的，确保每个子集 S 的贡献被合理计算。

(这个系数的作用就是让 "大子集" 和 "小子集" 的贡献被合理加权)

SHAP值

SHAP（SHapley Additive exPlanations）图是一种用于解释机器学习模型预测结果的可视化工具。它基于Shapley值理论，能够为每个特征分配一个贡献值，从而帮助我们理解模型的决策过程。以下是关于SHAP图的详细介绍：

1. SHAP图的基本原理

SHAP图的核心是Shapley值，它来源于博弈论，用于衡量每个特征在模型预测中的贡献度。
Shapley值的计算考虑了所有可能的特征组合，确保每个特征的贡献值是公平且合理的。
SHAP图通过可视化这些贡献值，帮助我们直观地理解哪些特征对模型的预测结果影响最大，以及这些特征是如何影响预测的。

2. SHAP图的类型

Summary Plot（总结图）：

这是最常用的SHAP图类型，用于展示所有特征对模型预测的总体影响。
每一行代表一个特征，特征按其对模型预测的平均影响大小排序。
每个点的颜色表示特征值的大小（通常红色表示高值，蓝色表示低值），点的位置表示该特征对预测的贡献值。
通过Summary Plot，我们可以快速识别哪些特征对模型的预测影响最大，以及这些特征的值如何影响预测结果。

Dependence Plot（依赖图）：

用于分析某个特定特征对模型预测的影响。
横轴表示特征值，纵轴表示该特征的SHAP值（即对预测的贡献值）。
通过这条曲线，我们可以看到特征值的变化如何影响模型的预测结果。例如，特征值越高，模型的预测值可能越高或越低。
这种图可以帮助我们理解特征与预测之间的非线性关系。

Force Plot（力图）：

主要用于解释单个预测结果。
以条形图的形式展示每个特征对预测结果的正向或负向贡献。
通过这种图，我们可以清楚地看到每个特征是如何推动或抑制模型的预测结果的。
力图非常适合用于解释复杂的模型预测，尤其是在需要向非技术用户解释模型决策时。

应用举例

现在我们来分析每个特征的贡献

dart 复制代码

import shap
import numpy as np
from sklearn.ensemble import RandomForestRegressor
# 生成随机数据
np.random.seed(0)
# 特征数量
n_features = 5  
# 样本数量
n_samples = 100  
# 生成特征矩阵 X，形状为 (n_samples, n_features)
X = np.random.rand(n_samples, n_features)  
# 生成目标变量 y，这里简单假设 y 与特征有线性关系并加噪声
y = 2 * X[:, 0] + 3 * X[:, 1] - 1 * X[:, 2] + np.random.randn(n_samples)

# 训练一个随机森林回归模型（你也可以替换成其他模型，如分类模型）
model = RandomForestRegressor()
model.fit(X, y)

# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(model)
# 计算 SHAP 值
shap_values = explainer.shap_values(X)

# 绘制 Summary Plot
shap.summary_plot(shap_values, X, feature_names=[f"Feature_{i}" for i in range(n_features)])

代码说明

数据生成：

使用 numpy 生成随机的特征矩阵 X（形状为 (n_samples, n_features) ）和目标变量 y 。这里为了简单，让 y 与部分特征有线性关系并添加了噪声，实际应用中可以根据需求构造更复杂的数据。

n_features 控制特征数量，n_samples 控制样本数量，可按需调整。

模型训练：

使用 scikit - learn 中的 RandomForestRegressor 训练一个随机森林回归模型，你也可以替换成其他支持的模型（如 RandomForestClassifier 用于分类任务，或者 XGBRegressor 、LGBMRegressor 等树模型，shap 对树模型的解释支持较好，也支持一些线性模型等）。

SHAP 值计算：

shap.TreeExplainer 专门用于解释树模型（如果是其他模型，可使用 shap.LinearExplainer 、shap.KernelExplainer 等对应的解释器）。

explainer.shap_values(X) 计算每个样本每个特征的 SHAP 值。

绘制 Summary Plot：

shap.summary_plot 函数接收 SHAP 值、特征矩阵 X 以及特征名称（通过 feature_names 参数指定，方便可视化时显示有意义的特征名）来绘制总结图。图中每一行对应一个特征，按特征对模型预测的平均影响大小排序，点的颜色表示特征值大小，位置表示该特征对预测的贡献值，帮助快速识别重要特征及特征值如何影响预测。

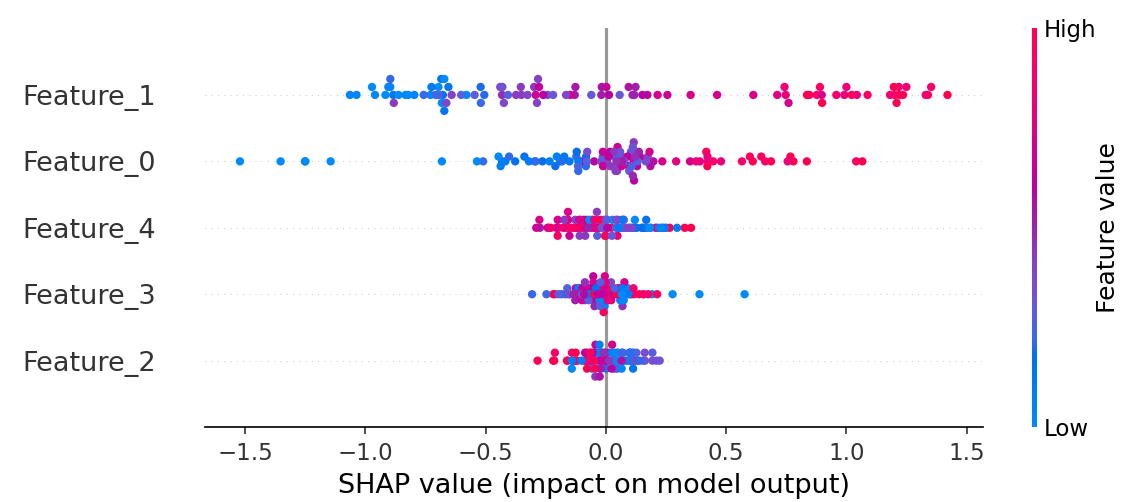
SHAP图说明

1. 基本结构："特征 - 影响 - 取值"

Y 轴（行）：按 "特征重要性" 排序的特征（越靠上的特征对模型影响越大）。

X 轴：SHAP 值（特征对模型预测结果的 "贡献值"），正值拉预测结果上升，负值拉预测结果下降。

颜色：特征值的大小（红高蓝低，右侧色条标注 Feature Value 对应关系）。

2. 全局规律："模型依赖的关键模式"

从图中可总结模型的 "决策逻辑"：

Feature_1 是强影响特征：

高值（红）几乎都让预测上升，低值（蓝）几乎都让预测下降 → 模型非常依赖 Feature_1 的取值判断。

Feature_0 有反向作用：

低值（蓝）强烈拉低预测，高值（红）对预测的推动较弱 → 模型对 Feature_0 的 "高值" 不敏感，但 "低值" 会明显抑制预测。

其他特征（如 Feature_2）：

SHAP 值集中在 0 附近 → 对预测的影响整体较小，模型决策更少依赖它们。

注：每个散点对应 "一个样本中，该特征的 SHAP 值"