【机器学习③】 | CNN篇

0 序言

本文将系统讲解卷积神经网络（CNN）的核心原理 ，以及LeNet-5 、AlexNet 、GoogLeNet 、ResNet 四大经典网络的结构、实现与应用。通过PyTorch代码示例，从基础原理到实际操作，帮助读者理解CNN如何处理多维数据 、经典网络的设计逻辑及实现方法，读完可掌握CNN的核心概念与落地技能。

1 CNN的原理

深度学习中，深度神经网络（DNN）在处理图像等多维数据时存在局限，而卷积神经网络（CNN）通过特殊结构解决了这一问题。本章将从DNN与CNN的差异出发，解析CNN的核心组件及工作机制。

1.1 从DNN到CNN

1.1.1 卷积层与汇聚

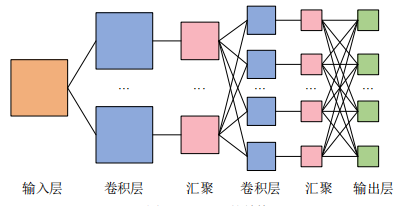
从图片这里能知道，DNN的相邻层神经元全连接，而CNN多了卷积层（Convolution）和汇聚（Pooling）。

所以从这里也能知道单个卷积层的典型结构：卷积层-激活函数-（汇聚），其中汇聚可省略。

1.1.2 CNN专攻多维数据

DNN处理图像时需将多维数据拉平为1维，但这样会丢失空间特征；
CNN的卷积层可保持输入数据维数，以多维形式接收和输出数据，保留空间特征。

1.2 卷积层

1.2.1 内部参数：权重（卷积核）

卷积核是卷积层的核心权重，输入数据与卷积核通过逐元素乘积后求和完成卷积运算。

比如说：

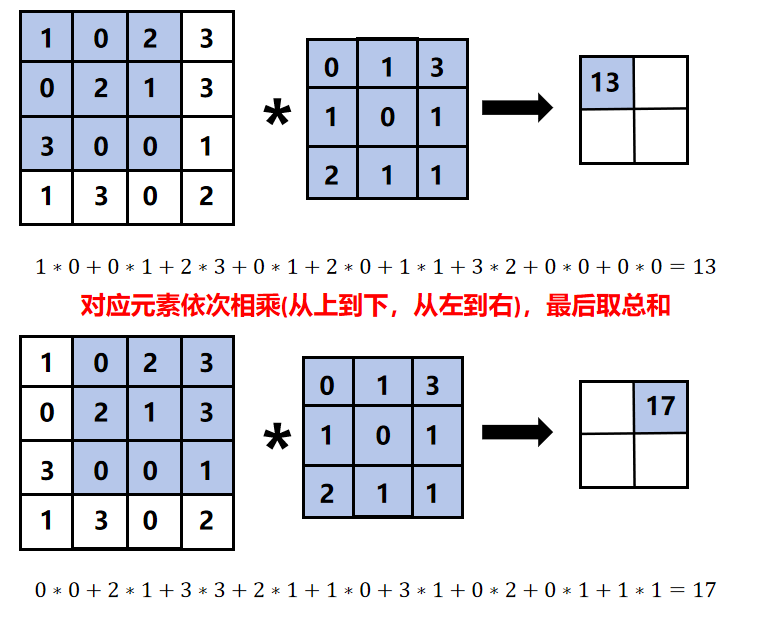
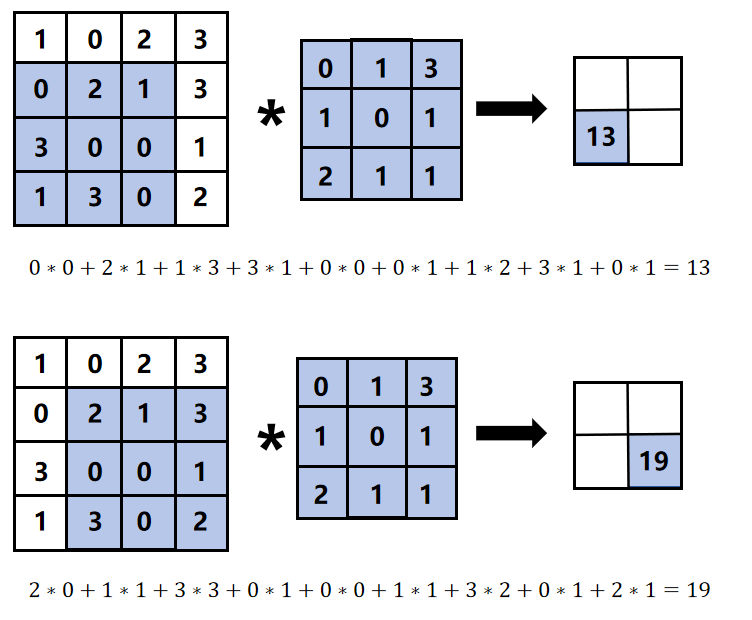
所以结果就是：

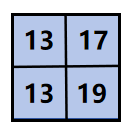
1.2.2 内部参数：偏置

卷积运算后需叠加偏置，偏置为常数，作用于整个输出结果。

1.2.3 外部参数：填充（Padding）

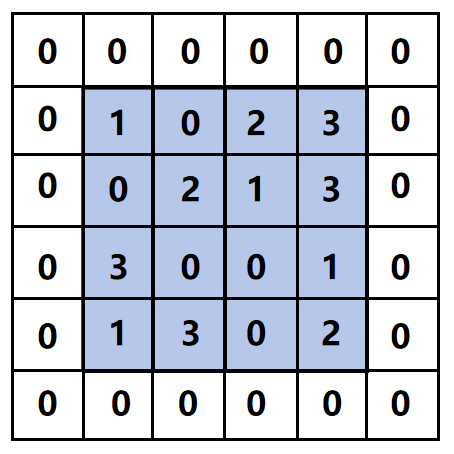
为避免多次卷积后图像尺寸过小，在输入数据周围填充固定值（如0）。
示例：4×4输入填充0后，尺寸变为6×6。

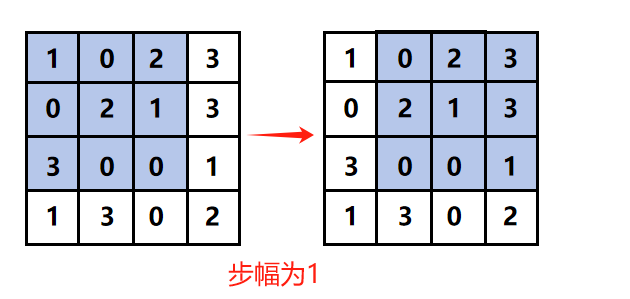
1.2.4 外部参数：步幅（Stride）

卷积核移动的间隔，步幅为1时逐像素移动，步幅为2时间隔1像素移动。
步幅增大会减小输出尺寸。

1.2.5 输入与输出尺寸的关系

设输入尺寸为（H, W），卷积核尺寸（FH, FW），填充P，步幅S，则输出尺寸（OH, OW）为：
{OH=H+2P−FHS+1OW=W+2P−FWS+1 \begin{cases} OH = \frac{H + 2P - FH}{S} + 1 \\ OW = \frac{W + 2P - FW}{S} + 1 \end{cases} {OH=SH+2P−FH+1OW=SW+2P−FW+1

1.3 多通道

1.3.1 多通道输入

彩色图像等三维数据含通道维度（如RGB为3通道），输入与滤波器的通道数需一致。

多通道卷积后输出为二维，即多个单通道卷积结果求和。

1.3.2 多通道输出

为保留多维特征，需多通道输出，通过多个滤波器（数量为输出通道数）实现。

每个输出通道对应一个偏置，单独作用于该通道。

1.4 汇聚（Pooling）

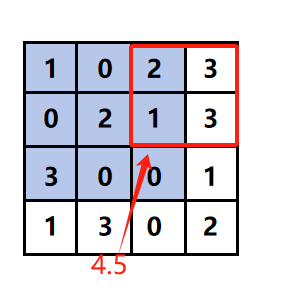
1.4.1 平均汇聚

对指定窗口（如2×2）内元素取平均值，步幅为2时输出尺寸减半。

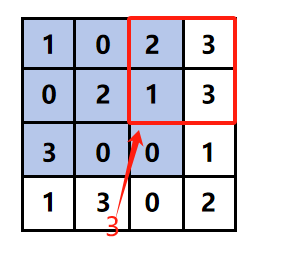
1.4.2 最大值汇聚

对指定窗口内元素取最大值，同样步幅为2时输出尺寸减半。

1.4.3 特点

无学习参数，仅提取局部特征；不改变通道数，仅减小高和宽。

1.5 尺寸变换总结

1.5.1 卷积层尺寸变换

输入尺寸（C, H, W），滤波器尺寸（FN, C, FH, FW），输出尺寸（FN, OH, OW），计算公式相同。

{OH=H+2P−FHS+1OW=W+2P−FWS+1 \begin{cases} OH = \frac{H + 2P - FH}{S} + 1 \\ OW = \frac{W + 2P - FW}{S} + 1 \end{cases} {OH=SH+2P−FH+1OW=SW+2P−FW+1

1.5.2 汇聚层尺寸变换

输入尺寸（C, H, W），步幅S，输出尺寸（C, OH, OW），其中：

{OH=H/SOW=W/S \begin{cases} OH = H / S \\ OW = W / S \end{cases} {OH=H/SOW=W/S

2 LeNet-5

通过第一章，我们理解了CNN的核心原理（卷积层、汇聚层、多通道等）。但理论需结合实践，LeNet-5作为早期经典CNN，成功应用于手写数字识别，本章将详解其结构及PyTorch实现，帮助理解CNN的运作流程。

2.1 网络结构

2.1.1 整体结构

共7层，输入28×28图像，输出10类（0-9）概率，层结构如下：

层	类型	卷积核/参数	步幅	填充	激活函数	输出尺寸
C1	卷积层	6×1×5×5	1	2	tanh	6×28×28
S2	平均汇聚	2×2	2	-	-	6×14×14
C3	卷积层	16×6×5×5	1	-	tanh	16×10×10
S4	平均汇聚	2×2	2	-	-	16×5×5
C5	卷积层	120×16×5×5	1	-	tanh	120×1×1
F6	全连接层	-	-	-	tanh	84
Out	全连接层	-	-	-	Softmax	10

2.2 制作数据集

python 复制代码

import torch
from torch.utils.data import DataLoader
from torchvision import transforms, datasets

# 数据转换：转为Tensor并归一化
transform = transforms.Compose([
    transforms.ToTensor(),  # 转为张量
    transforms.Normalize(0.1307, 0.3081)  # 归一化（均值，标准差）
])

# 下载MNIST数据集（手写数字）
train_Data = datasets.MNIST(
    root='D:/Jupyter/dataset/mnist/',  # 存储路径
    train=True,  # 训练集
    download=True,  # 不存在则下载
    transform=transform  # 应用转换
)
test_Data = datasets.MNIST(
    root='D:/Jupyter/dataset/mnist/',
    train=False,  # 测试集
    download=True,
    transform=transform
)

# 数据加载器（批次处理）
train_loader = DataLoader(train_Data, shuffle=True, batch_size=256)  # 训练集打乱
test_loader = DataLoader(test_Data, shuffle=False, batch_size=256)  # 测试集不打乱

2.3 搭建神经网络

python 复制代码

import torch.nn as nn

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        # 定义网络层
        self.net = nn.Sequential(
            # C1: 卷积层（输入1通道，输出6通道，5×5卷积核，填充2）
            nn.Conv2d(1, 6, kernel_size=5, padding=2),
            nn.Tanh(),  # 激活函数
            # S2: 平均汇聚（2×2窗口，步幅2）
            nn.AvgPool2d(kernel_size=2, stride=2),
            # C3: 卷积层（输入6通道，输出16通道，5×5卷积核）
            nn.Conv2d(6, 16, kernel_size=5),
            nn.Tanh(),
            # S4: 平均汇聚
            nn.AvgPool2d(kernel_size=2, stride=2),
            # C5: 卷积层（输入16通道，输出120通道，5×5卷积核）
            nn.Conv2d(16, 120, kernel_size=5),
            nn.Tanh(),
            nn.Flatten(),  # 展平为一维
            # F6: 全连接层（120→84）
            nn.Linear(120, 84),
            nn.Tanh(),
            # 输出层（84→10）
            nn.Linear(84, 10)
        )
    
    def forward(self, x):
        return self.net(x)  # 前向传播

# 测试网络结构
X = torch.rand(size=(1, 1, 28, 28))  # 模拟输入（1样本，1通道，28×28）
model = CNN()
for layer in model.net:
    X = layer(X)
    print(layer.__class__.__name__, '输出形状:', X.shape)

这里的网络层可以见下图：

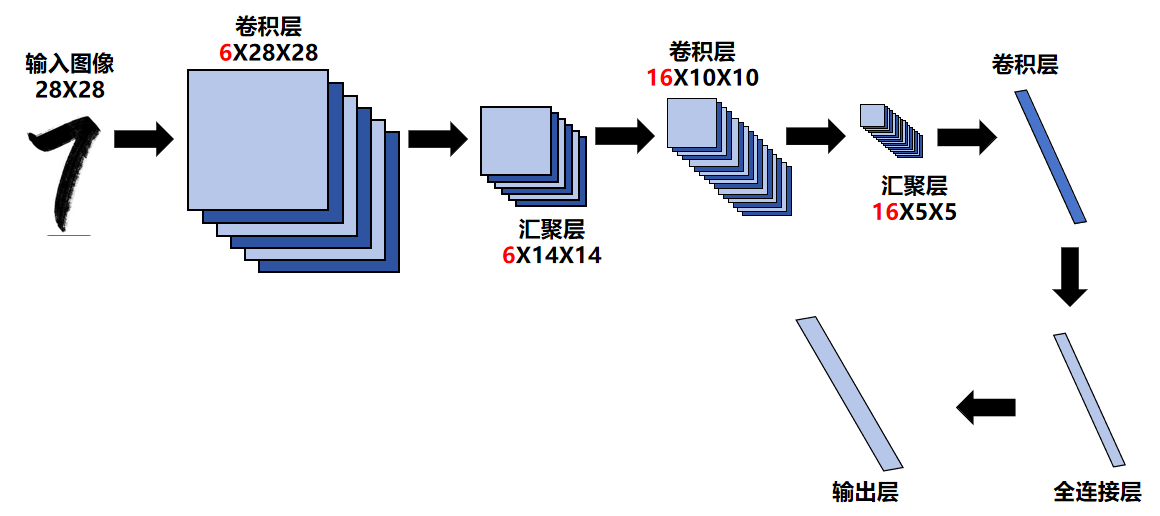
2.4 训练网络

python 复制代码

# 损失函数（交叉熵，自带Softmax）
loss_fn = nn.CrossEntropyLoss()
# 优化器（SGD，学习率0.9）
optimizer = torch.optim.SGD(model.parameters(), lr=0.9)

# 训练参数
epochs = 5
losses = []  # 记录损失

# 移至GPU
model = model.to('cuda:0')

for epoch in range(epochs):
    for x, y in train_loader:
        x, y = x.to('cuda:0'), y.to('cuda:0')  # 数据移至GPU
        pred = model(x)  # 前向传播
        loss = loss_fn(pred, y)  # 计算损失
        losses.append(loss.item())  # 记录损失
        
        optimizer.zero_grad()  # 清空梯度
        loss.backward()  # 反向传播
        optimizer.step()  # 更新参数

2.5 测试网络

python 复制代码

correct = 0
total = 0
with torch.no_grad():  # 关闭梯度计算
    for x, y in test_loader:
        x, y = x.to('cuda:0'), y.to('cuda:0')
        pred = model(x)  # 预测
        _, predicted = torch.max(pred.data, dim=1)  # 取概率最大类别
        correct += torch.sum(predicted == y)  # 统计正确数
        total += y.size(0)  # 总样本数

print(f'测试集准确率: {100 * correct / total} %')  # 输出准确率（示例：97.94%）

2.6 完整程序

python 复制代码

# 导入必要的库
import torch  # 导入PyTorch核心库
import torch.nn as nn  # 导入神经网络模块
from torch.utils.data import DataLoader  # 导入数据加载工具
from torchvision import transforms  # 导入数据转换工具
from torchvision import datasets  # 导入数据集
import matplotlib.pyplot as plt  # 导入绘图库


# 1. 数据准备：加载并预处理MNIST数据集
def prepare_data():
    # 定义数据转换 pipeline：将图像转为张量并归一化
    # transforms.ToTensor()：将PIL图像转为Tensor（维度为[C, H, W]，值归一化到0-1）
    # transforms.Normalize()：用均值和标准差进一步归一化，MNIST的推荐值为(0.1307, 0.3081)
    transform = transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize(0.1307, 0.3081)
    ])
    
    # 加载MNIST训练集（手写数字数据集）
    # root：数据集存储路径
    # train=True：加载训练集
    # download=True：如果路径中没有数据集，自动下载
    # transform：应用上述数据转换
    train_dataset = datasets.MNIST(
        root='./dataset/mnist/',  # 建议将数据集放在项目下的dataset文件夹，方便管理
        train=True,
        download=True,
        transform=transform
    )
    
    # 加载MNIST测试集
    # train=False：加载测试集
    test_dataset = datasets.MNIST(
        root='./dataset/mnist/',
        train=False,
        download=True,
        transform=transform
    )
    
    # 创建数据加载器（按批次加载数据，支持打乱和并行）
    # batch_size=256：每次加载256个样本
    # shuffle=True：训练集打乱顺序，增强泛化能力
    # 测试集无需打乱（shuffle=False）
    train_loader = DataLoader(
        train_dataset,
        batch_size=256,
        shuffle=True
    )
    test_loader = DataLoader(
        test_dataset,
        batch_size=256,
        shuffle=False
    )
    
    return train_loader, test_loader


# 2. 定义LeNet-5网络结构
class LeNet5(nn.Module):
    def __init__(self):
        super(LeNet5, self).__init__()  # 继承父类初始化方法
        # 定义网络层序列（按LeNet-5结构依次堆叠）
        self.net = nn.Sequential(
            # C1层：卷积层（提取低级特征，如边缘、纹理）
            # in_channels=1：输入为灰度图（1通道）
            # out_channels=6：输出6个特征图（6个卷积核）
            # kernel_size=5：卷积核大小5×5
            # padding=2：边缘填充2像素，保持输出尺寸与输入一致（28×28）
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
            nn.Tanh(),  # 激活函数：引入非线性，tanh是LeNet-5原用激活函数
            
            # S2层：平均汇聚层（下采样，减少特征图尺寸，保留关键信息）
            # kernel_size=2：2×2窗口
            # stride=2：步幅2，输出尺寸减半
            nn.AvgPool2d(kernel_size=2, stride=2),
            
            # C3层：卷积层（提取更复杂的特征）
            # in_channels=6：输入为S2的6个特征图
            # out_channels=16：输出16个特征图
            # kernel_size=5：5×5卷积核（无填充，尺寸进一步缩小）
            nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
            nn.Tanh(),  # 激活函数
            
            # S4层：平均汇聚层（再次下采样）
            nn.AvgPool2d(kernel_size=2, stride=2),
            
            # C5层：卷积层（实际相当于全连接层，特征图压缩为1×1）
            # in_channels=16：输入为S4的16个特征图
            # out_channels=120：输出120个特征图
            # kernel_size=5：5×5卷积核（5×5特征图经过5×5卷积后变为1×1）
            nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5),
            nn.Tanh(),  # 激活函数
            
            nn.Flatten(),  # 展平层：将120×1×1的特征图转为120维向量
            
            # F6层：全连接层（整合高级特征）
            nn.Linear(in_features=120, out_features=84),  # 120→84
            nn.Tanh(),  # 激活函数
            
            # 输出层：全连接层（最终分类）
            nn.Linear(in_features=84, out_features=10)  # 84→10（对应0-9共10类）
        )
    
    # 前向传播：定义数据在网络中的流动路径
    def forward(self, x):
        return self.net(x)  # 直接通过定义的层序列传播


# 3. 测试网络结构是否正确（验证各层输出尺寸）
def test_network_structure():
    # 创建一个模拟输入：1个样本，1通道，28×28像素（MNIST图像尺寸）
    dummy_input = torch.randn(size=(1, 1, 28, 28))
    # 初始化网络
    model = LeNet5()
    # 打印各层输出形状，验证是否符合预期
    print("网络各层输出形状验证：")
    x = dummy_input
    for layer in model.net:
        x = layer(x)
        # 打印层名称和输出形状（[样本数, 通道数, 高度, 宽度]或[样本数, 特征数]）
        print(f"{layer.__class__.__name__}: {x.shape}")


# 4. 训练网络
def train_model(model, train_loader, epochs=5, lr=0.9):
    # 定义损失函数：交叉熵损失（适用于分类任务，自带Softmax激活）
    criterion = nn.CrossEntropyLoss()
    # 定义优化器：随机梯度下降（SGD），学习率0.9（LeNet-5经典参数）
    optimizer = torch.optim.SGD(model.parameters(), lr=lr)
    
    # 记录训练损失，用于后续绘图
    train_losses = []
    
    # 开始训练
    print("\n开始训练...")
    for epoch in range(epochs):  # 遍历训练轮次
        model.train()  # 切换到训练模式（启用dropout等，此处无dropout但规范操作）
        total_loss = 0.0
        
        for batch_idx, (images, labels) in enumerate(train_loader):
            # 前向传播：输入图像，得到预测结果
            outputs = model(images)
            # 计算损失：预测结果与真实标签的差异
            loss = criterion(outputs, labels)
            
            # 反向传播与参数更新
            optimizer.zero_grad()  # 清空上一轮梯度（避免累积）
            loss.backward()  # 计算梯度（反向传播）
            optimizer.step()  # 根据梯度更新参数
            
            # 记录损失
            train_losses.append(loss.item())
            total_loss += loss.item()
            
            # 每100个批次打印一次中间结果
            if (batch_idx + 1) % 100 == 0:
                print(f"轮次 [{epoch+1}/{epochs}], 批次 [{batch_idx+1}/{len(train_loader)}], "
                      f"当前批次损失: {loss.item():.4f}")
        
        # 打印本轮平均损失
        avg_loss = total_loss / len(train_loader)
        print(f"轮次 [{epoch+1}/{epochs}] 平均损失: {avg_loss:.4f}")
    
    # 绘制训练损失曲线
    plt.figure(figsize=(10, 4))
    plt.plot(train_losses, label='训练损失')
    plt.xlabel('批次')
    plt.ylabel('损失值')
    plt.title('训练损失变化曲线')
    plt.legend()
    plt.show()
    
    return model, train_losses


# 5. 测试网络（评估准确率）
def test_model(model, test_loader):
    model.eval()  # 切换到评估模式（关闭dropout等）
    correct = 0  # 记录正确预测的样本数
    total = 0    # 记录总样本数
    
    # 关闭梯度计算（测试阶段无需计算梯度，节省内存和时间）
    with torch.no_grad():
        print("\n开始测试...")
        for images, labels in test_loader:
            # 前向传播得到预测结果
            outputs = model(images)
            # 取概率最大的类别作为预测结果（dim=1表示按行取最大值）
            _, predicted = torch.max(outputs.data, 1)
            # 累加总样本数和正确样本数
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    
    # 计算准确率
    accuracy = 100 * correct / total
    print(f"测试集准确率: {accuracy:.2f}%")
    return accuracy


# 主函数：串联所有步骤
def main():
    # 步骤1：准备数据
    train_loader, test_loader = prepare_data()
    print("数据准备完成，训练集样本数：", len(train_loader.dataset), 
          "测试集样本数：", len(test_loader.dataset))
    
    # 步骤2：验证网络结构
    test_network_structure()
    
    # 步骤3：初始化模型
    model = LeNet5()
    print("\nLeNet-5模型初始化完成")
    
    # 步骤4：训练模型
    trained_model, losses = train_model(model, train_loader, epochs=5)
    
    # 步骤5：测试模型
    test_model(trained_model, test_loader)


# 程序入口：当脚本直接运行时执行主函数
if __name__ == "__main__":
    main()

运行结果如下：

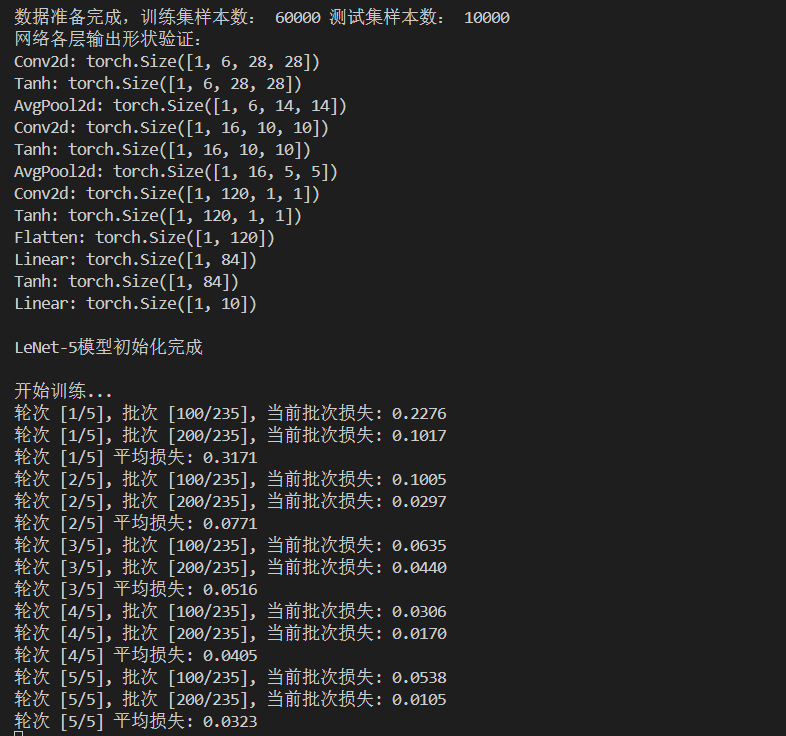
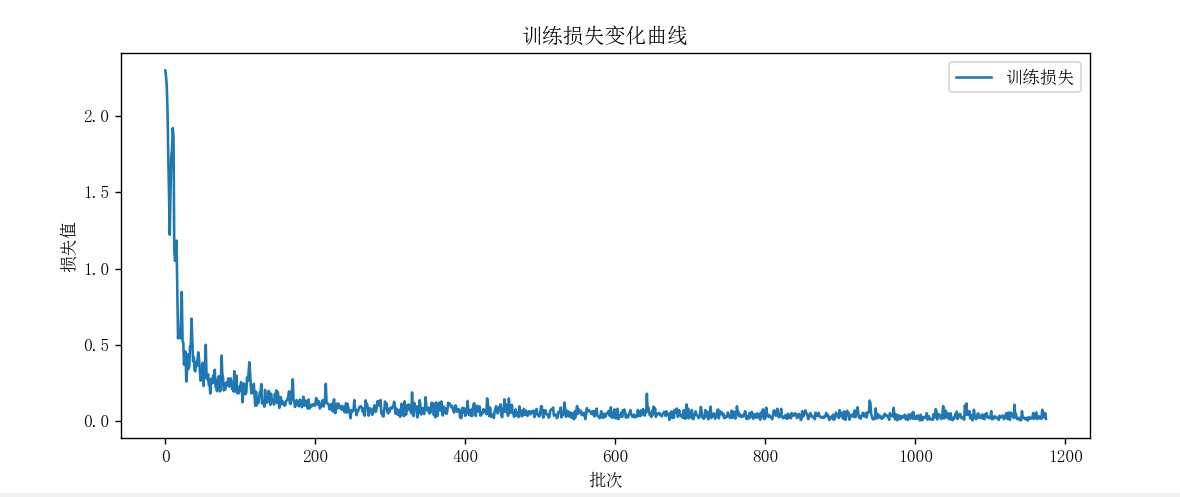
本次LeNet-5训练实验中，首先完成MNIST数据集加载（训练集60000样本、测试集10000样本），并通过模拟输入验证网络结构：各层输出尺寸（如卷积层、汇聚层、全连接层的维度变化）完全符合LeNet-5设计逻辑，确保模型搭建正确。训练阶段历经5个轮次，损失值从首轮平均0.3171持续下降至末轮0.0323 ，再结合损失曲线可见：前期因模型从随机初始化快速学习特征，损失呈断崖式下降；后期因SGD优化器（学习率0.9较高）导致参数更新步幅大，损失出现震荡，但整体仍趋于收敛，证明模型有效提取了手写数字的分类特征，最后的准确率为98.48%。

当然，从该实验完整验证了LeNet-5的经典设计在MNIST任务上的学习能力，也体现了高学习率下优化过程的典型波动特性。

3 AlexNet

通过第二章，我们掌握了LeNet-5的实现，但其结构较简单，难以处理复杂图像。AlexNet作为首个现代深度CNN，引入ReLU、Dropout等技术，大幅提升性能，本章将详解其结构及基于MNIST的适配实现。

3.1 网络结构

3.1.1 整体结构（适配MNIST）

输入1×224×224（MNIST图像放大后），输出10类，层结构如下：

层	类型	滤波器/参数	步幅	填充	激活函数	输出尺寸
C1	卷积层	96×1×11×11	4	1	ReLU	96×54×54
S2	最大汇聚	3×3	2	-	-	96×26×26
C3	卷积层	256×96×5×5	1	2	ReLU	256×26×26
S4	最大汇聚	3×3	2	-	-	256×12×12
C5	卷积层	384×256×3×3	1	1	ReLU	384×12×12
C6	卷积层	384×384×3×3	1	1	ReLU	384×12×12
C7	卷积层	256×384×3×3	1	1	ReLU	256×12×12
S8	最大汇聚	3×3	2	-	-	256×5×5
F9	全连接层	-	-	-	ReLU	4096
F10	全连接层	-	-	-	ReLU	4096
Out	全连接层	-	-	-	Softmax	10

3.2 制作数据集（适配FashionMNIST）

python 复制代码

# 数据转换：转为Tensor、 resize至224×224、归一化
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Resize(224),  # 放大至224×224
    transforms.Normalize(0.1307, 0.3081)
])

# 加载FashionMNIST数据集
train_Data = datasets.FashionMNIST(
    root='D:/Jupyter/dataset/mnist/',
    train=True,
    download=True,
    transform=transform
)
test_Data = datasets.FashionMNIST(
    root='D:/Jupyter/dataset/mnist/',
    train=False,
    download=True,
    transform=transform
)

# 数据加载器
train_loader = DataLoader(train_Data, shuffle=True, batch_size=128)
test_loader = DataLoader(test_Data, shuffle=False, batch_size=128)

3.3 搭建神经网络

python 复制代码

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.net = nn.Sequential(
            # C1: 卷积层（1→96通道，11×11卷积核，步幅4，填充1）
            nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1),
            nn.ReLU(),  # 用ReLU替代tanh，缓解梯度消失
            # S2: 最大汇聚
            nn.MaxPool2d(kernel_size=3, stride=2),
            # C3: 卷积层（96→256通道，5×5卷积核，填充2）
            nn.Conv2d(96, 256, kernel_size=5, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3, stride=2),
            # C5-C7: 连续卷积层
            nn.Conv2d(256, 384, kernel_size=3, padding=1),
            nn.ReLU(),
            nn.Conv2d(384, 384, kernel_size=3, padding=1),
            nn.ReLU(),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(),
            # S8: 最大汇聚
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Flatten(),
            # 全连接层+Dropout（防止过拟合）
            nn.Linear(6400, 4096),
            nn.ReLU(),
            nn.Dropout(p=0.5),  # 随机丢弃50%神经元
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(p=0.5),
            nn.Linear(4096, 10)  # 输出10类
        )
    
    def forward(self, x):
        return self.net(x)

3.4 训练与测试网络

训练流程同LeNet-5（学习率0.1，epochs=10），测试准确率约99.30%。

4 GoogLeNet

AlexNet通过加深网络提升性能，但滤波器超参数（如尺寸）需手动调整，难以最优。GoogLeNet引入Inception块，通过并行路径自动学习最佳特征提取方式，本章详解其结构与实现。

4.1 网络结构

4.1.1 Inception块（核心组件）

4条并行路径，自动选择最优特征提取方式：
1. 1×1卷积（分支1）
2. 1×1卷积→3×3卷积→3×3卷积（分支2）
3. 1×1卷积→5×5卷积（分支3）
4. 1×1卷积（分支4）

输出为4条路径结果拼接，1×1卷积用于降维，降低复杂度。

4.2 制作数据集（同AlexNet，用FashionMNIST）

4.3 搭建神经网络

python 复制代码

# 定义Inception块
class Inception(nn.Module):
    def __init__(self, in_channels):
        super(Inception, self).__init__()
        # 分支1：1×1卷积（降维）
        self.branch1 = nn.Conv2d(in_channels, 16, kernel_size=1)
        # 分支2：1×1→3×3→3×3
        self.branch2 = nn.Sequential(
            nn.Conv2d(in_channels, 16, kernel_size=1),
            nn.Conv2d(16, 24, kernel_size=3, padding=1),
            nn.Conv2d(24, 24, kernel_size=3, padding=1)
        )
        # 分支3：1×1→5×5
        self.branch3 = nn.Sequential(
            nn.Conv2d(in_channels, 16, kernel_size=1),
            nn.Conv2d(16, 24, kernel_size=5, padding=2)
        )
        # 分支4：1×1卷积
        self.branch4 = nn.Conv2d(in_channels, 24, kernel_size=1)
    
    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)
        return torch.cat([branch1, branch2, branch3, branch4], 1)  # 拼接通道

# 定义GoogLeNet网络
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.net = nn.Sequential(
            nn.Conv2d(1, 10, kernel_size=5),  # 初始卷积
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2),
            Inception(10),  # 加入Inception块
            nn.Conv2d(88, 20, kernel_size=5),  # 88为Inception输出通道数
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2),
            Inception(20),
            nn.Flatten(),
            nn.Linear(1408, 10)  # 全连接输出
        )
    
    def forward(self, x):
        return self.net(x)

4.4 训练与测试网络

训练流程类似（学习率0.1，epochs=10），最终得到到测试准确率约98.92%。

5 ResNet

GoogLeNet通过并行路径优化特征提取，但深层网络仍面临梯度消失问题（梯度随层数增加趋于0）。ResNet引入残差块，通过跳跃连接缓解梯度消失，本章详解其原理与实现。

5.1 网络结构

5.1.1 残差块（核心组件）

结构：输入x通过权重层得到f(x)，输出为f(x)+x（加跳跃连接），再经ReLU激活。
作用：反向传播时梯度为dy/dx + 1，避免梯度消失，支持更深网络。

5.2 制作数据集（同前，用FashionMNIST）

5.3 搭建神经网络

python 复制代码

# 定义残差块
class ResidualBlock(nn.Module):
    def __init__(self, channels):
        super(ResidualBlock, self).__init__()
        self.net = nn.Sequential(
            nn.Conv2d(channels, channels, kernel_size=3, padding=1),  # 保持通道数
            nn.ReLU(),
            nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        )
    
    def forward(self, x):
        y = self.net(x)
        return nn.functional.relu(x + y)  # 跳跃连接：x + 权重层输出

# 定义ResNet网络
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.net = nn.Sequential(
            nn.Conv2d(1, 16, kernel_size=5),  # 初始卷积
            nn.ReLU(),
            nn.MaxPool2d(2),
            ResidualBlock(16),  # 残差块1
            nn.Conv2d(16, 32, kernel_size=5),
            nn.ReLU(),
            nn.MaxPool2d(2),
            ResidualBlock(32),  # 残差块2
            nn.Flatten(),
            nn.Linear(512, 10)  # 输出层
        )
    
    def forward(self, x):
        return self.net(x)

5.4 训练与测试网络

训练流程类似（学习率0.1，epochs=10），测试准确率约98.98%。

6 总结

本文从CNN的核心原理出发，解析了卷积层、多通道、汇聚等基础组件的工作机制，以及尺寸变换的计算逻辑。通过LeNet-5 、AlexNet 、GoogLeNet 、ResNet四个经典网络的实现，展示了CNN的发展脉络：从早期解决手写数字识别（LeNet-5），到引入现代技术（ReLU、Dropout，AlexNet），再到通过并行路径（Inception块，GoogLeNet）和跳跃连接（残差块，ResNet）优化深层网络性能。