模型拟合问题全解析：从欠拟合、过拟合到正则化（岭回归与拉索回归）

欠拟合过拟合

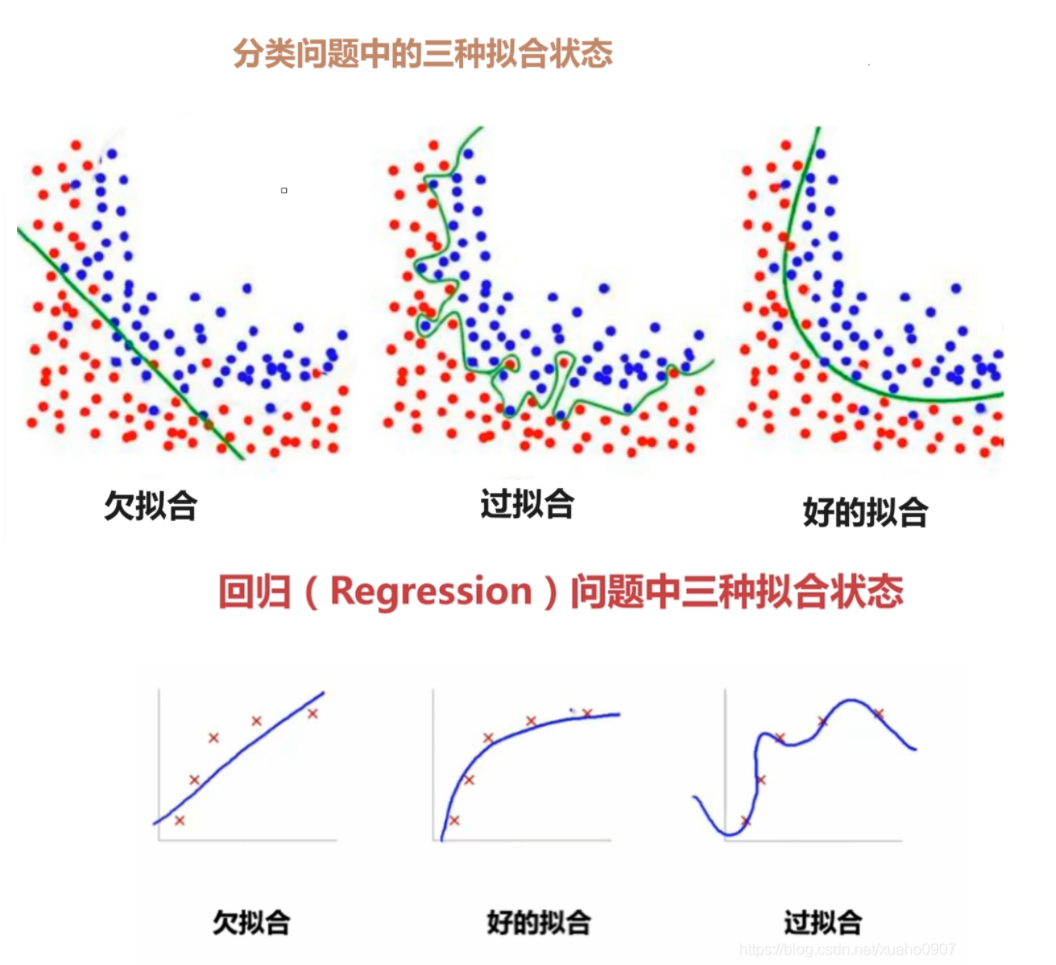
1欠拟合

欠拟合是指模型在训练数据上表现不佳，同时在新的未见过的数据上也表现不佳。这通常发生在模型过于简单，无法捕捉数据中的复杂模式时。欠拟合模型的表现特征如下：

训练误差较高。
测试误差同样较高。
模型可能过于简化，不能充分学习训练数据中的模式。

2过拟合

过拟合是指模型在训练数据上表现得非常好，但在新的未见过的数据上表现较差。这通常发生在模型过于复杂，以至于它不仅学习了数据中的真实模式，还学习了噪声和异常值。过拟合模型的表现特征如下：

训练误差非常低。
测试误差较高。
模型可能过于复杂，以至于它对训练数据进行了过度拟合。

3正则化

正则化就是防止过拟合，增加模型的鲁棒性 ，鲁棒是Robust 的音译，也就是强壮的意思。就像计算机软件在面临攻击、网络过载等情况下能够不死机不崩溃，这就是软件的鲁棒性,鲁棒性调优就是让模型拥有更好的鲁棒

性，也就是让模型的泛化能力和推广能力更加的强大。

比如,下面两个方程描述同一条直线,哪个更好?

y=0.5x1+0.6x2+0.7y=0.5x_1+0.6x_2+0.7y=0.5x1+0.6x2+0.7

y=5x1+6x2+7y=5x_1+6x_2+7y=5x1+6x2+7

第一个更好，因为下面的公式是上面的十倍，当w越小公式的容错的能力就越好。我们都知道人工智能中回归是有误差的,为了把误差降低而拟合出来的一个接近真实的公式,比如把一个测试数据[10,20]带入计算得到的值跟真实值会存在一定的误差,但是第二个方程会把误差放大,公式中y=WTxy = W^Txy=WTx，当xxx有一点错误，这个错误会通过w放大。但是w不能太小，当w太小时(比如都趋近0)，模型就没有意义了，无法应用。想要有一定的容错率又要保证正确率就要由正则项来发挥作用了!

所以**正则化(鲁棒性调优)**的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力，W在数值上越小越好，这样能抵抗数值的扰动。同时为了保证模型的正确率W又不能极小。因此将原来的损失函数加上一个惩罚项使得计算出来的模型W相对小一些，就是正则化。

这里面损失函数就是原来固有的损失函数，比如回归的话通常是MSE，然后在加上一部分惩罚项来使得计算出来的模型W相对小一些来带来泛化能力。

常用的惩罚项有L1正则项或者L2正则项:

L1=∣∣w∣∣1=∑i=1n∣wi∣L1=||w||1=\textstyle\sum{i=1}^{n}|w_i|L1=∣∣w∣∣1=∑i=1n∣wi∣ 对应曼哈顿距离

L2=∣∣w∣∣2=∑i=1nxip,X=(x1,x2,...xn)pL2=||w||2=\textstyle\sqrt[p]{\sum{i=1}^{n}x^p_i,X=(x_1,x_2,...x_n)}L2=∣∣w∣∣2=p∑i=1nxip,X=(x1,x2,...xn) 对应欧氏距离

其实L1L1L1 和L2L2L2 正则的公式在数学里面的意义就是范数,代表空间中向量到原点的距离

当我们把多元线性回归损失函数加上L2L2L2正则的时候，就诞生了Ridge岭回归。当我们把多元线性回归损失函数加上L1L1L1正则的时候，就孕育出来了Lasso回归。其实L1L1L1和L2L2L2正则项惩罚项可以加到任何算法的损失函数上面去提高计算出来模型的泛化能力的。

岭回归Ridge

1 损失函数公式

岭回归是失损函数通过添加所有权重的平方和的乘积(L2)来惩罚模型的复杂度。

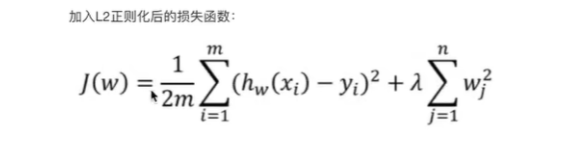
均方差除以2是因为方便求导，wjw_jwj指所有的权重系数, λ指惩罚型系数，又叫正则项力度

特点:

岭回归不会将权重压缩到零，这意味着所有特征都会保留在模型中，但它们的权重会被缩小。
适用于特征间存在多重共线性的情况。
岭回归产生的模型通常更为平滑，因为它对所有特征都有影响。

2 API

py 复制代码

具有L2正则化的线性回归-岭回归。
sklearn.linear_model.Ridge()
1 参数：
(1)alpha, default=1.0，正则项力度
(2)fit_intercept, 是否计算偏置， default=True
(3)solver, {'auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga', 'lbfgs'}, default='auto'
当值为auto,并且数据量、特征都比较大时，内部会随机梯度下降法。
(4)normalize：,default=True, 数据进行标准化，如果特征工程中已经做过标准化，这里就该设置为False
(5)max_iterint, default=None,梯度解算器的最大迭代次数，默认为15000

2 属性
coef_ 回归后的权重系数
intercept_ 偏置


说明:SGDRegressor也可以做岭回归的事情，比如SGDRegressor(penalty='l2',loss="squared_loss"),但是其中梯度下降法有些不同。所以推荐使用Ridge实现岭回归

3 示例

岭回归加载加利福尼亚住房数据集，进行回归预测

python 复制代码

# 岭回归 加载加利福尼亚住房数据集，进行回归预测
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error

from sklearn.datasets import fetch_california_housing
# 1)加载数据
housing = fetch_california_housing(data_home="./src")
print(housing)
# 2)划分训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(housing.data, housing.target, random_state=22)
# 3)标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4）岭回归预估器
estimator = Ridge(alpha=0.5, max_iter=10000)
estimator.fit(x_train, y_train)

# 5）得出模型
print("权重系数为：\n", estimator.coef_)  #权重系数与特征数一定是同样的个数。
print("偏置为：\n", estimator.intercept_)

# 6）模型评估
y_predict = estimator.predict(x_test)
print("预测的数据集：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

拉索回归Lasso

1 损失函数公式

Lasso回归是一种线性回归模型，它通过添加所有权重的绝对值之和(L1)来惩罚模型的复杂度。

Lasso回归的目标是最小化以下损失函数：

J(w)=12n∑i=1n(hw(xi)−yi)2+λ∑j=1p∣wj∣\text{J(w)}= \frac{1}{2n}\sum_{i=1}^n (h_w(x_i)-y_i)^2 + \lambda \sum_{j=1}^p |w_j|J(w)=2n1∑i=1n(hw(xi)−yi)2+λ∑j=1p∣wj∣

其中：

特点:

拉索回归可以将一些权重压缩到零，从而实现特征选择。这意味着模型最终可能只包含一部分特征。
适用于特征数量远大于样本数量的情况，或者当特征间存在相关性时，可以从中选择最相关的特征。
拉索回归产生的模型可能更简单，因为它会去除一些不重要的特征。

2 API

sklearn.linear_model.Lasso()

参数:

alpha (float, default=1.0) :
- 控制正则化强度；必须是非负浮点数。较大的 alpha 增加了正则化强度。
fit_intercept (bool, default=True) :
- 是否计算此模型的截距。如果设置为 False，则不会使用截距（即数据应该已经被居中）。
precompute (bool or array-like, default=False) :
- 如果为 True，则使用预计算的 Gram 矩阵来加速计算。如果为数组，则使用提供的 Gram 矩阵。
copy_X (bool, default=True) :
- 如果为 True，则复制数据 X，否则可能对其进行修改。
max_iter (int, default=1000) :
- 最大迭代次数。
tol (float, default=1e-4) :
- 精度阈值。如果更新后的系数向量减去之前的系数向量的无穷范数除以 1 加上更新后的系数向量的无穷范数小于 tol，则认为收敛。
warm_start (bool, default=False) :
- 当设置为 True 时，再次调用 fit 方法会重新使用之前调用 fit 方法的结果作为初始估计值，而不是清零它们。
positive (bool, default=False) :
- 当设置为 True 时，强制系数为非负。
random_state (int, RandomState instance, default=None) :
- 随机数生成器的状态。用于随机初始化坐标下降算法中的随机选择。
selection ({'cyclic', 'random'}, default='cyclic') :
- 如果设置为 'random'，则随机选择坐标进行更新。如果设置为 'cyclic'，则按照循环顺序选择坐标。

属性:

coef_
- 系数向量或者矩阵，代表了每个特征的权重。
**intercept_ **
- 截距项（如果 fit_intercept=True）。
**n_iter_ **
- 实际使用的迭代次数。
n_features_in_ (int) :
- 训练样本中特征的数量。

3 示例

python 复制代码

from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np

# 加载波士顿房价数据集
data = fetch_california_housing(data_home="./src")
X, y = data.data, data.target

# 划分训练集和测试集
X_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建Lasso回归模型
lasso = Lasso(alpha=0.1)  # alpha是正则化参数

# 训练模型
lasso.fit(X_train, y_train)

# 得出模型
print("权重系数为：\n", lasso.coef_)  #权重系数与特征数一定是同样的个数。
print("偏置为：\n", lasso.intercept_)

#模型评估
y_predict = lasso.predict(x_test)
print("预测的数据集：\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

总结

本文围绕模型拟合问题及解决方案展开。欠拟合因模型简单，无法捕捉数据模式，表现为训练和测试误差均较高；过拟合则因模型复杂，过度学习噪声，呈现训练误差低而测试误差高的特点。

正则化是解决过拟合的关键，通过在损失函数中加入惩罚项（L1或L2正则项），控制权重大小，在牺牲部分训练正确率的同时，提升模型泛化能力------既保证一定容错性，又避免权重过小导致模型失效。

具体而言，岭回归（Ridge）采用L2正则项（权重平方和），不将权重压缩至0，保留所有特征，适用于特征存在多重共线性的场景，通过sklearn.linear_model.Ridge实现；拉索回归（Lasso）使用L1正则项（权重绝对值和），可将部分权重压缩至0，实现特征选择，适用于特征数量多或需筛选关键特征的情况，对应API为sklearn.linear_model.Lasso。两者均通过正则化参数调整惩罚强度，优化模型性能。