K-Means 聚类算法详解与实战
1. 什么是 K-Means?
K-Means 是一种常用的无监督学习聚类算法,用于将数据集划分为 K 个簇(Cluster)。它的目标是让簇内的数据尽量相似,簇间的数据尽量不同。
应用场景包括:
-
客户分群(Marketing Segmentation)
-
图像压缩(Image Compression)
-
文档聚类(Document Clustering)
-
异常检测(Anomaly Detection)
2. 算法原理
K-Means 的核心思想是:
-
随机选择 K 个点作为初始聚类中心(质心,Centroid)。
-
计算每个样本到各质心的距离,将样本分配到最近的质心所在的簇。
-
重新计算每个簇的质心(即簇内所有点的均值)。
-
重复步骤 2 和 3,直到簇不再变化或达到最大迭代次数。
其优化目标是最小化簇内的平方误差和(Sum of Squared Errors, SSE):
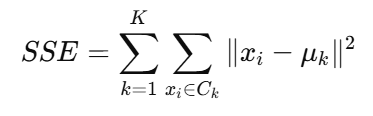
其中:
-
Ck :第 k 个簇
-
μk :第 k 个簇的质心
3. 算法流程
-
选择 K 值(簇的数量)。
-
初始化 K 个质心。
-
分配样本到最近质心。
-
更新质心为簇内样本均值。
-
检查收敛条件:
-
质心变化小于阈值
-
或达到最大迭代次数
-
4. K 值的选择方法
K-Means 需要提前设定 K ,但这个值怎么选呢?
常用方法:
-
肘部法(Elbow Method)
绘制 K 对 SSE 的曲线,当下降幅度明显减缓的位置就是"肘部"。
-
轮廓系数(Silhouette Coefficient)
取值范围 [-1, 1],越接近 1 聚类效果越好。
5. 优缺点
优点:
-
简单高效,易于实现
-
对大数据集表现较好(时间复杂度 O(n) ~ O(nkt))
缺点:
-
需要提前设定 K
-
对异常值和噪声敏感
-
假设簇是球形且大小相近
-
容易陷入局部最优(可用多次初始化改善)
6.KMeans 超参数详解
from sklearn.cluster import KMeans
model = KMeans(
n_clusters=8,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-4,
verbose=0,
random_state=None,
copy_x=True,
algorithm='lloyd'
)| 超参数 | 作用描述 | 类型 | 默认值 | 备注与建议 |
|---|---|---|---|---|
n_clusters |
聚类簇的数量 K | int | 8 | 需根据数据选择,常用肘部法或轮廓系数确定 |
init |
质心初始化方法 | {'k-means++','random'} 或 ndarray | 'k-means++' | 推荐用 'k-means++',提升收敛速度和效果 |
n_init |
不同随机质心初始化运行次数 | int | 10 | 值越大越稳定,默认10次足够,多数情况下不用调 |
max_iter |
单次运行最大迭代次数 | int | 300 | 超过该迭代次数则停止,一般300够用 |
tol |
收敛容差阈值 | float | 1e-4 | 质心移动小于该值停止迭代,调小提高精度但慢 |
verbose |
迭代过程输出等级 | int | 0 | 0不输出,1或2输出详细调试信息 |
random_state |
随机种子,保证结果复现 | int 或 RandomState | None | 实验需固定,常用42等数字 |
copy_x |
是否复制输入数据 | bool | True | False节省内存但修改原数据 |
algorithm |
K-Means算法实现版本 | {'lloyd', 'elkan'} | 'lloyd' | 'elkan'更快适合小稠密数据,稀疏数据用'lloyd' |
7. Python 实战案例
我们用 scikit-learn 对二维数据进行聚类,并可视化结果。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 1. 生成模拟数据 (这一部分不用在意)
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=42)
# 2. 创建并训练KMeans模型
kmeans = KMeans(n_clusters=4, random_state=42, n_init=10)
kmeans.fit(X)
# 3. 获取聚类结果
y_kmeans = kmeans.predict(X)
# 4. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
# 绘制质心
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X', label='质心')
plt.title("K-Means")
plt.legend()
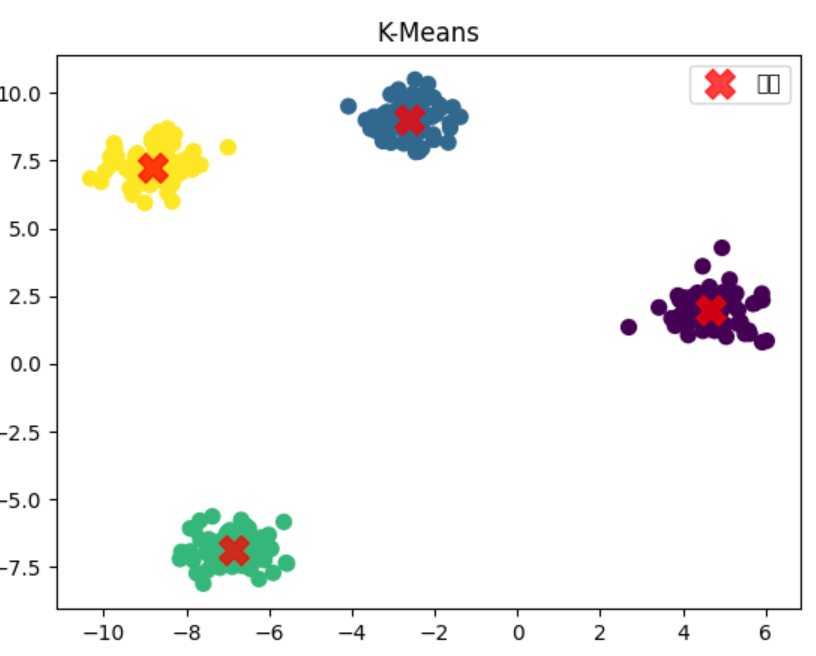
plt.show()运行结果:
-
数据被分为 4 类,不同颜色代表不同簇
-
红色 X 是质心位置
8. 代码细节说明
-
n_clusters:指定簇的数量 K -
random_state:确保结果可复现 -
n_init:KMeans 会多次随机初始化质心,取最佳结果,默认值从1提升到10以提高稳定性 -
cluster_centers_:存储最终的质心坐标 -
labels_:每个样本的簇标签
9. 改进方法
-
K-Means++:优化质心初始化,减少陷入局部最优的概率
-
Mini-Batch K-Means:适合大规模数据,使用小批量数据迭代更新质心
-
谱聚类、DBSCAN:在簇形状不规则时效果更好
10. 总结
K-Means 是机器学习中最常用的聚类算法之一,适合簇形状较为规则、数量已知的场景。它简单、高效,但也有对 K 值和噪声敏感等缺点,实际应用时往往需要结合数据分布和改进方法使用。