Day18 推断聚类后簇的类型

@浙大疏锦行
聚类后的分析：推断簇的类型
知识点回顾：

推断簇含义的2个思路：先选特征和后选特征
通过可视化图形借助ai定义簇的含义
科研逻辑闭环:通过精度判断特征工程价值

**作业：**参考示例代码对心脏病数据集采取类似操作，并且评估特征工程后模型效果有无提升。

如何通过聚类构造有价值的特征工程：

现在需要给这个簇赋予实际的含义，一般当你赋予实际含义的时候，你需要根据某几个特征来赋予，但是源数据特征很多，如何选择特征呢？有2种思路：

你最开始聚类的时候，就选择了你想最后用来确定簇含义的特征，那么你需要选择一些特征来进行聚类，那么你最后确定簇含义的特征就是这几个特征，而非全部。如你想聚类消费者购买习惯，那么他过去的消费记录、购买记录、购买金额等等，这些特征都与消费者购买习惯有关，你可以使用这些特征来确定簇含义，一些其他的特征，如消费者年龄，工作行业则不考虑。----适用于你本身就有构造某些明确含义的特征的情况。
最开始用全部特征来聚类，把其余特征作为 x，聚类得到的簇类别作为标签构建监督模型，进而根据重要性筛选特征，来确定要根据哪些特征赋予含义。---使用于你想构造什么，目前还不清楚。

昨天进行的心脏病的聚类两种思路都可以，但是因为昨天是全部特征来聚类的，所以今天先尝试第二种思路。

python 复制代码

print(X.columns)

Index(['age', 'trestbps', 'chol', 'thalach', 'oldpeak', 'sex_1', 'cp_1',
       'cp_2', 'cp_3', 'fbs_1', 'restecg_1', 'restecg_2', 'exang_1', 'slope_1',   
       'slope_2', 'ca_1', 'ca_2', 'ca_3', 'ca_4', 'thal_1', 'thal_2', 'thal_3',   
       'thalach_age_ratio', 'bp_chol_risk', 'st_depression_ratio',
       'KMeans_Cluster'],
      dtype='object')

python 复制代码

x1= X.drop('KMeans_Cluster',axis=1) # 删除聚类标签列
y1 = X['KMeans_Cluster']
# 构建随机森林，用shap重要性来筛选重要性
import shap
from sklearn.ensemble import RandomForestClassifier  # 随机森林分类器
model = RandomForestClassifier(n_estimators=100, random_state=42)  # 随机森林模型
model.fit(x1, y1)  # 训练模型,此时无需在意准确率 直接全部数据用来训练了
shap.initjs()
# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(x1) # 这个计算耗时
print(shap_values.shape) # 第一维是样本数，第二维是特征数，第三维是类别数

在运行上述代码时会发生报错，因为在使用随机森林分类器时，通过 explainer.shap_values(x1) 获取的 shap_values 是一个列表（而非数组），每个元素对应一个类别的 SHAP 值数组。由于列表没有 shape 属性，直接调用 shap_values.shape 导致报错 'list' object has no attribute 'shape' 。

关键知识点补充：
SHAP 值的返回格式：

对于分类模型（如 RandomForestClassifier）， shap_values 是列表，长度等于类别数，每个元素是形状为 (样本数, 特征数) 的数组。
对于回归模型（如 RandomForestRegressor）， shap_values 直接是二维数组，形状为 (样本数, 特征数) ，可直接访问 shape 。
正确访问分类模型的 SHAP 值形状：
访问特定类别： shap_values[0].shape （查看第一个类别的形状）。
转换为三维数组： np.array(shap_values).shape （输出 (类别数, 样本数, 特征数) ）。
应用场景：

随机森林 + SHAP 常用于特征重要性分析，通过 SHAP 值可直观理解每个特征对不同类别预测的影响方向和程度。
扩展提示：

使用 explainer(x1) 可返回 Explanation 对象，其 values 属性在分类任务中也是列表，但提供了更多可视化功能（如 shap.summary_plot() ）。

python 复制代码

x1= X.drop('KMeans_Cluster',axis=1) # 删除聚类标签列
y1 = X['KMeans_Cluster']
# 构建随机森林，用shap重要性来筛选重要性
import shap
from sklearn.ensemble import RandomForestClassifier  # 随机森林分类器
model = RandomForestClassifier(n_estimators=100, random_state=42)  # 随机森林模型
model.fit(x1, y1)  # 训练模型,此时无需在意准确率 直接全部数据用来训练了
shap.initjs()
# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(x1) # 这个计算耗时
# 转换为三维数组并查看形状
shap_values_array = np.array(shap_values)
print(shap_values_array.shape)  # 输出 (类别数, 样本数, 特征数)

修改代码运行结果如下，需要注意的是，输出的第一类是类别数，第二类是样本数，第三类是特征数

python 复制代码

(3, 303, 25)

python 复制代码

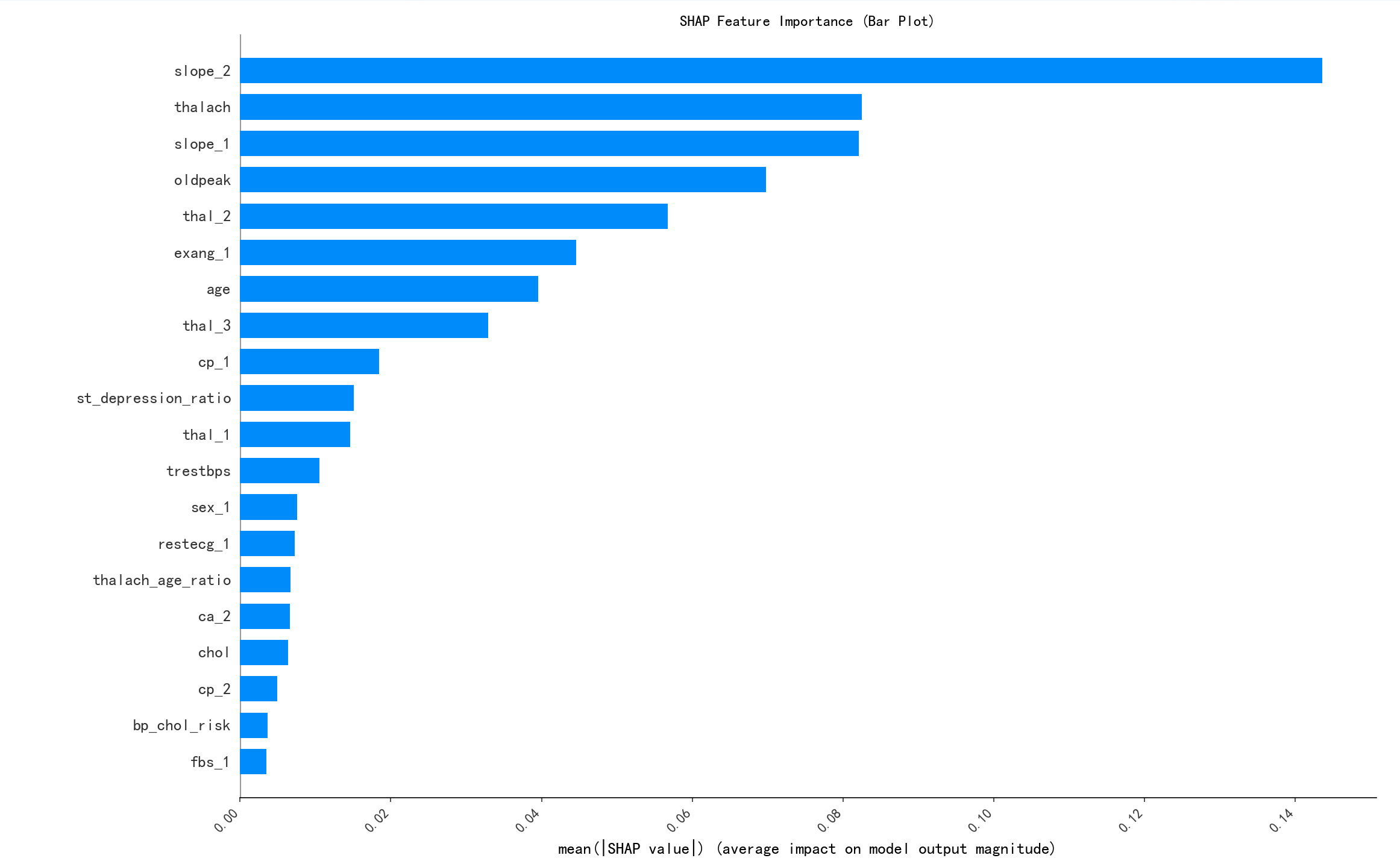
# --- 1. SHAP 特征重要性条形图 (Summary Plot - Bar) --- 
print("--- 1. SHAP 特征重要性条形图 ---") 
# 设置图表大小，增加宽度以显示完整特征名称
plt.figure(figsize=(12, 8))
# 使用转换后的三维数组并选择第一个类别
shap.summary_plot(shap_values_array[0], x1, plot_type="bar", show=False)  
plt.title("SHAP Feature Importance (Bar Plot)") 
# 旋转x轴标签以避免重叠
plt.xticks(rotation=45, ha='right')
# 调整布局，确保所有元素都能正确显示
plt.tight_layout()
plt.show()

通过shap条形图来观察特征的重要性，选择前五个特征进行判断离散和连续，考虑后续的特征工程

python 复制代码

# --- 判断前5个重要特征的类型 --- 
print("\n--- 判断前5个重要特征的类型 --- ")

# 假设前5个重要特征名称（根据SHAP条形图）
# 注意：请根据您实际的SHAP条形图结果修改这些特征名称
selected_features = ['slope_2', 'thalach', 'slope_1', 'oldpeak', 'thal_2']

print("前5个重要特征的类型判断:")
for feature in selected_features:
    # 检查特征是否存在于x1中
    if feature in x1.columns:
        unique_count = x1[feature].nunique()
        print(f'{feature} 的唯一值数量: {unique_count}')
        if unique_count < 10:  # 经验阈值，可以调整
            print(f'{feature} 可能是离散型变量')
        else:
            print(f'{feature} 可能是连续型变量')
    else:
        print(f'警告: 特征 {feature} 不存在于数据中')


--- 判断前5个重要特征的类型 ---
前5个重要特征的类型判断:
slope_2 的唯一值数量: 2
slope_2 可能是离散型变量
thalach 的唯一值数量: 91
thalach 可能是连续型变量
slope_1 的唯一值数量: 2
slope_1 可能是离散型变量
oldpeak 的唯一值数量: 5
oldpeak 可能是离散型变量
thal_2 的唯一值数量: 2
thal_2 可能是离散型变量

python 复制代码

# --- 总样本中的前五个重要性特征分布图 --- 
print("\n--- 总样本中的前五个重要性特征分布图 --- ")
import matplotlib.pyplot as plt

# 定义前五个重要特征（根据SHAP条形图结果）
top5_feature_names = ['slope_2', 'thalach', 'slope_1', 'oldpeak', 'thal_2']

# 创建2行3列的子图网格（足够容纳5个特征）
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()  # 将2D数组展平为1D数组以便迭代

# 绘制前五个重要特征的直方图
for i, feature in enumerate(top5_feature_names[:5]):  # 确保只取前5个特征
    if feature in x1.columns:
        # 绘制直方图
        axes[i].hist(x1[feature], bins=20)
        axes[i].set_title(f'{feature} 分布图')
        axes[i].set_xlabel(feature)
        axes[i].set_ylabel('频率')
    else:
        print(f'警告: 特征 {feature} 不存在于数据中')
        axes[i].axis('off')  # 关闭不存在特征的子图

# 隐藏第6个子图（如果有）
if len(axes) > 5:
    for i in range(5, len(axes)):
        axes[i].axis('off')

plt.tight_layout()
plt.show()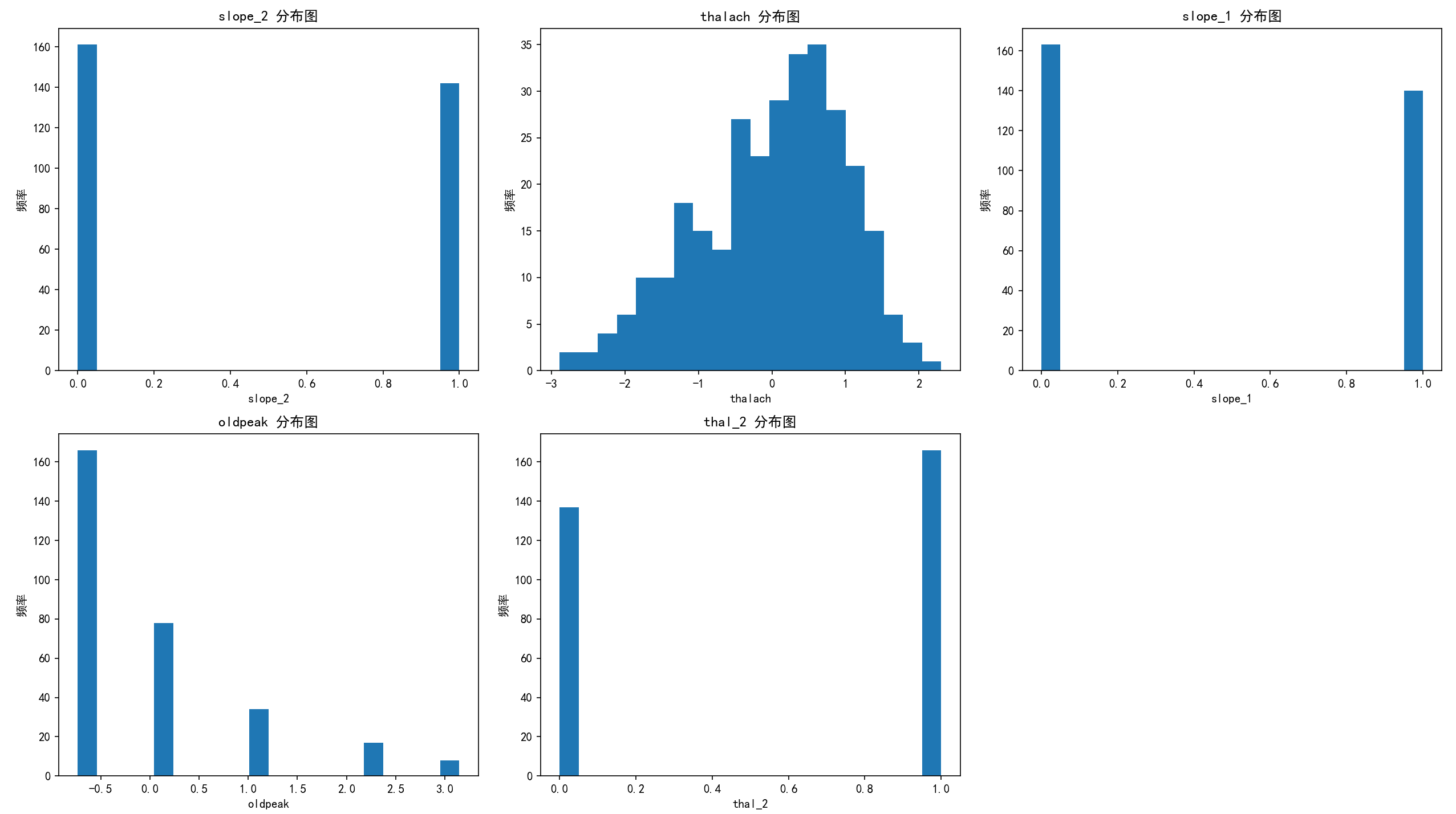

了解一下每个聚类的分布情况，查看是否均衡，为后续分析提供信息。

python 复制代码

print(X[['KMeans_Cluster']].value_counts())

KMeans_Cluster
0                 159
1                 126
2                  18
Name: count, dtype: int64

python 复制代码

# 分别筛选出每个簇的数据
X_cluster0 = X[X['KMeans_Cluster'] == 0]
X_cluster1 = X[X['KMeans_Cluster'] == 1]
X_cluster2 = X[X['KMeans_Cluster'] == 2]


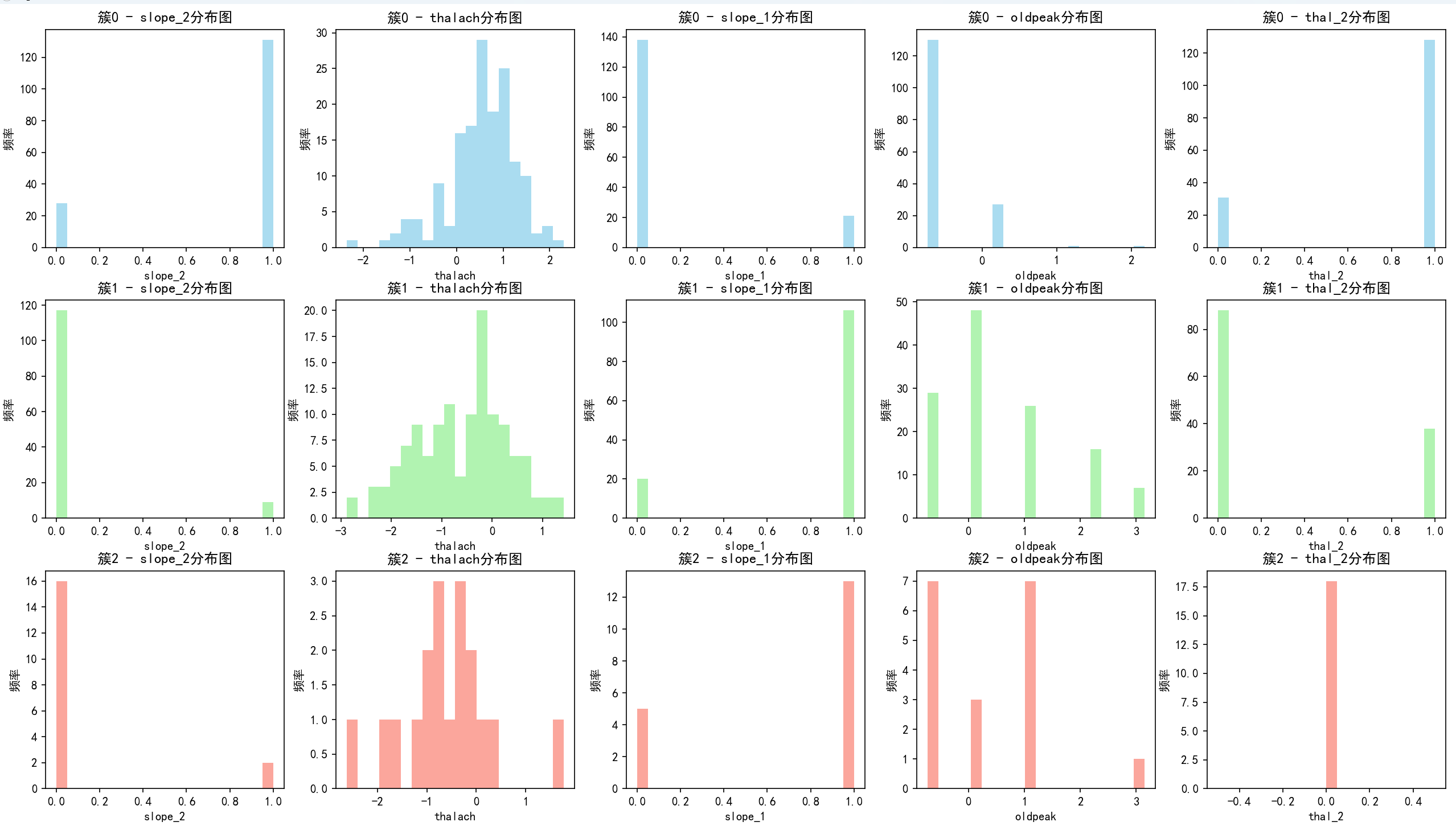
# 创建画布，3行5列的子图（每行代表一个簇，每列代表一个特征）
fig, axes = plt.subplots(3, 5, figsize=(20, 12))

# 绘制簇0的特征分布图
for i, feature in enumerate(top5_feature_names):
    axes[0, i].hist(X_cluster0[feature], bins=20, color='skyblue', alpha=0.7)
    axes[0, i].set_title(f'簇0 - {feature}分布图')
    axes[0, i].set_xlabel(feature)
    axes[0, i].set_ylabel('频率')

# 绘制簇1的特征分布图
for i, feature in enumerate(top5_feature_names):
    axes[1, i].hist(X_cluster1[feature], bins=20, color='lightgreen', alpha=0.7)
    axes[1, i].set_title(f'簇1 - {feature}分布图')
    axes[1, i].set_xlabel(feature)
    axes[1, i].set_ylabel('频率')

# 绘制簇2的特征分布图
for i, feature in enumerate(top5_feature_names):
    axes[2, i].hist(X_cluster2[feature], bins=20, color='salmon', alpha=0.7)
    axes[2, i].set_title(f'簇2 - {feature}分布图')
    axes[2, i].set_xlabel(feature)
    axes[2, i].set_ylabel('频率')

plt.tight_layout()
plt.show()

做出每一个簇的前五个重要性的特征分布图，通过ai来分析如何进行特征总结，来进行后续的特征工程。

第一个簇 - 心脏健康稳定型
- 特征总结 ：slope_2呈双峰分布，thalach取值范围广，slope_1多为小值，oldpeak普遍小，thal_2呈双峰分布。整体心脏相关生理指标分布有特点，无明显集中风险特征，心脏健康基础表现稳定。各指标分布差异体现人群在心脏功能相关特征上有一定多样性，但无突出风险集中趋势，反映心脏健康状态相对均衡。
- 定义依据 ：从slope（斜率，反映心脏功能相关）、thalach（最大心率）等关键心脏指标看，分布虽有特点但无突出风险集中趋势，故定义为 "心脏健康稳定型"。
第二个簇 - 心脏指标集中型
- 特征总结 ：slope_2多为小值，thalach取值集中（呈现较为明显的单峰分布），slope_1小值情况更普遍，oldpeak分布相对分散，thal_2多为小值。心脏相关指标在部分维度呈现集中化表现，指标特征相对一致。thalach等核心指标取值集中，反映该簇人群在心脏应激能力（以最大心率为体现）等方面相似性高，生理特征一致性强，疾病风险相对稳定且可预测。
- 定义依据 ：thalach等核心指标取值集中，slope类指标小值占比高，指标一致性强于其他簇。因指标集中体现生理特征一致、疾病风险易评估，因此定义为 "心脏指标集中型"。
第三个簇 - 心脏指标多峰分散型
- 特征总结 ：slope_2多为小值，thalach呈多峰分布（在几个特定值区间内频率较高，取值相对分散），slope_1有分散性，oldpeak集中分布，thal_2多为小值。心脏指标在不同维度呈现多峰、分散等复杂分布，指标特征多样。多峰分散的thalach等指标，反映人群心脏应激能力差异大，涵盖不同健康状况、生活习惯或遗传背景个体，疾病风险复杂难概括。
- 定义依据 ：thalach等指标多峰分散，与前两个簇指标分布模式差异明显。基于复杂多样的指标分布特征（体现生理特征异质性、疾病风险难预测），定义为 "心脏指标多峰分散型"。

这样算完成了自己的一次特征工程，要注意不是簇有几类就有几个新特征，进行聚类后只得到了一个新的特征就是"KMeans_Cluster"，是KMeans聚类(k=3)生成的簇标签特征，取值0/1/2，代表样本在特征空间中的相似性分组。