快速上手大模型：机器学习2（一元线性回归、代价函数、梯度下降法）

目录

[1 一元线性回归](#1 一元线性回归)

[1.1 定义](#1.1 定义)

[1.2 例子](#1.2 例子)

[2 代价函数（Cost function）](#2 代价函数（Cost function）)

[3 梯度下降算法（Gradiend descent algorithm）](#3 梯度下降算法（Gradiend descent algorithm）)

[3.1 引言](#3.1 引言)

[3.2 梯度下降表达式](#3.2 梯度下降表达式)

[3.3 图像理解](#3.3 图像理解)

[3.4 学习率的选择](#3.4 学习率的选择)

[3.5 线性回归中的梯度下降](#3.5 线性回归中的梯度下降)

[3.6 批量梯度下降（"Batch" gradient descent）](#3.6 批量梯度下降（“Batch” gradient descent）)

---

1 一元线性回归

1.1 定义

另m为训练集的数量（多少组数据），x是输入变量，y是输出变量（目标变量：指输入特征下的预测结果）；(x,y)表示一个训练样本，表示训练集的第i个训练样本。这里一元是指只有一个输入变量。

一元线性回归是拟定一个线性函数f=wx+b（w,b为模型参数），使尽可能多的点在直线上并使代价函数最低。

1.2 例子

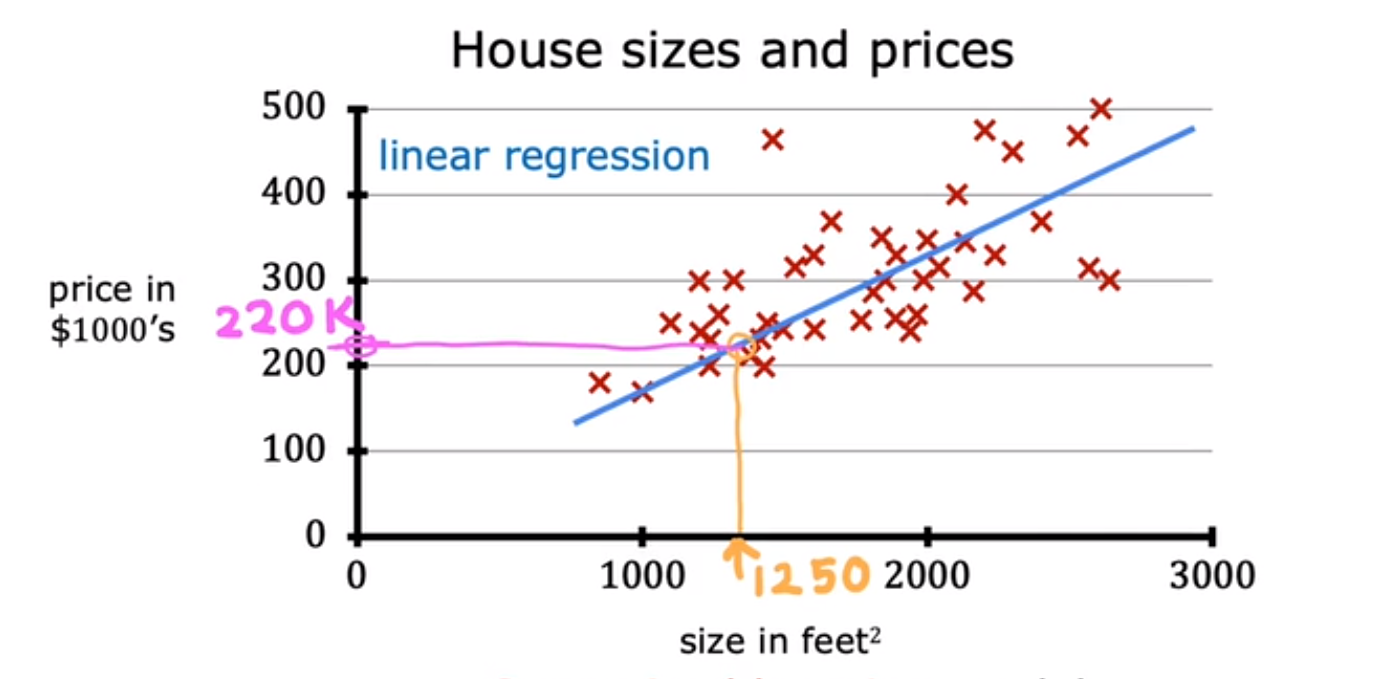
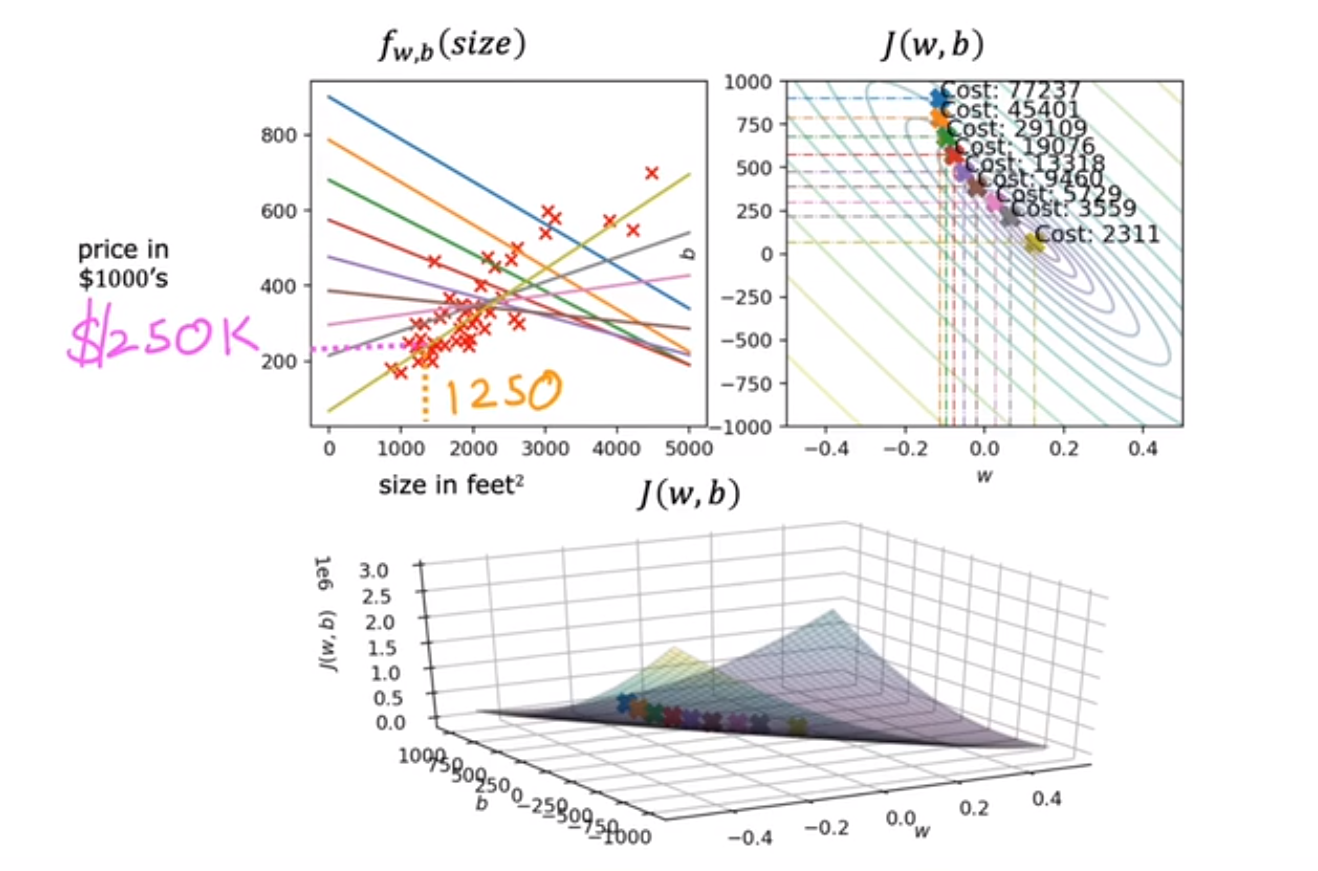
房产面积与价格，输入变量房产面积、输出变量房价，通过给定多组数据，拟合成一条线性函数f。当再次输入某一房产面积时，输出估计的房价。

前期通过多组数据进行训练，从而做到后面可以预测房价的功能。

2 代价函数（Cost function）

如上房价-面积示例，拟合该训练集的模型为线性函数，w,b为模型参数、也称系数、权重，可修改，直到找到一组w,b满足预测接近目标y。

代价函数式：,m为训练集样本数量。亦可表示为 。找w,b多少的时候J最小。

3 梯度下降算法（Gradiend descent algorithm）

3.1 引言

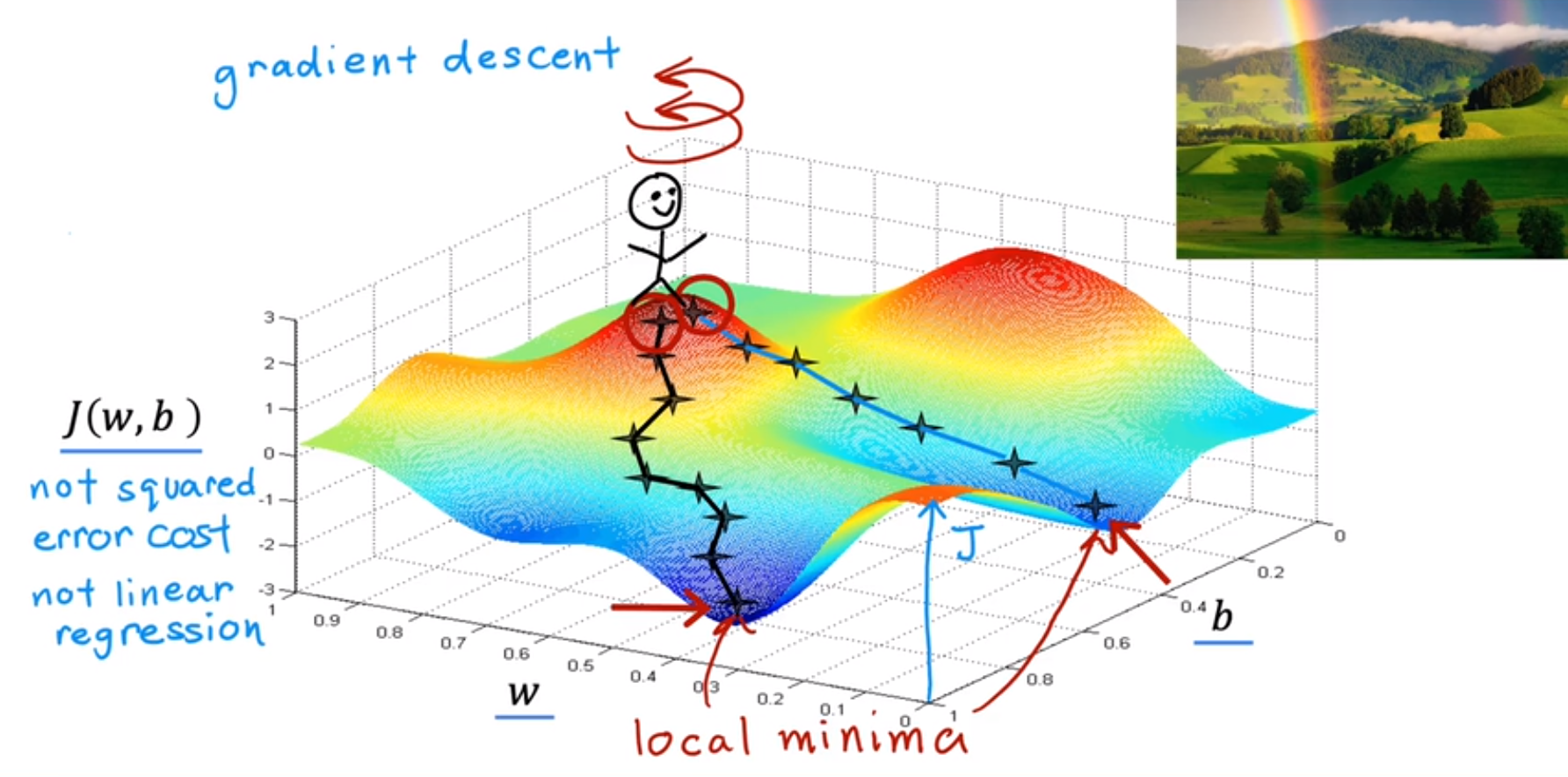
寻找代价函数J最小的方法。的函数如图，山顶上有个小人从不同点出发，以最快的速度达到谷地。

3.2 梯度下降表达式

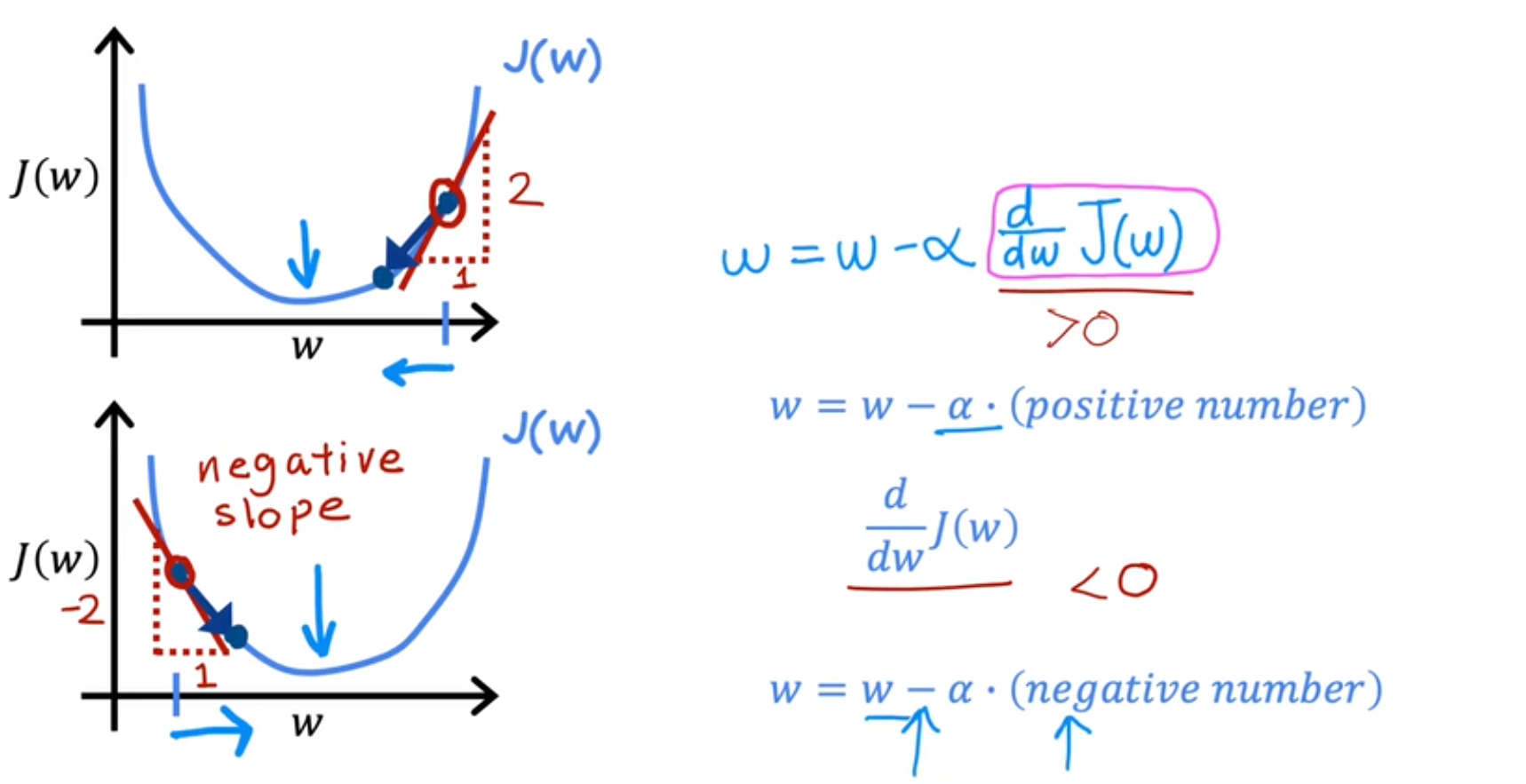
式中称为学习率，其是就是求偏导，下文会对其进行详述。梯度下降原理其是就是不断更新w,b直到收敛。

代码表示：

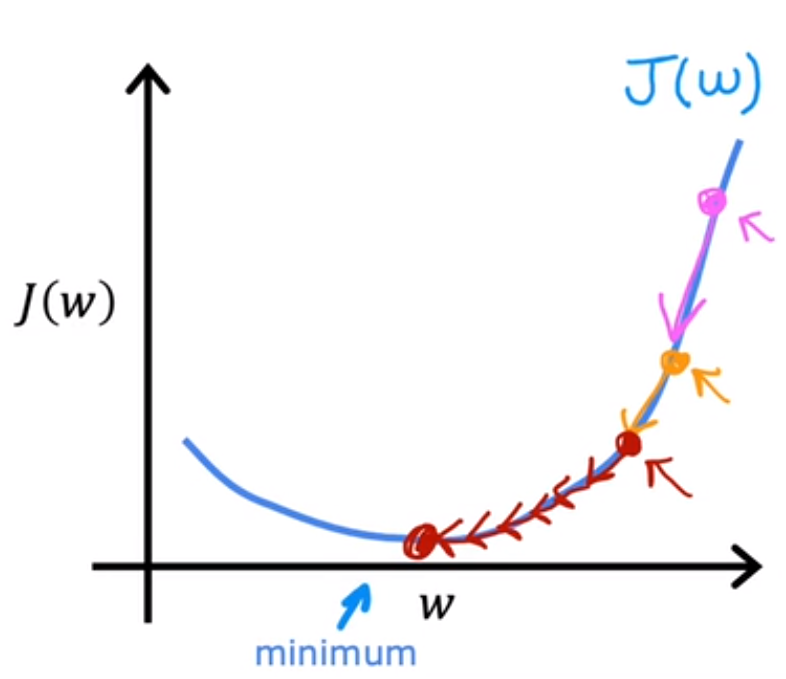
3.3 图像理解

先令b=0，只考虑w的影响。最上面图起始点为右侧，根据w关系式，当不断迭代学习率时，w不断减小，直到J达到最低点；下图同理，起始点右侧，当不断迭代学习率时，w不断增大，直到J达到最低点。

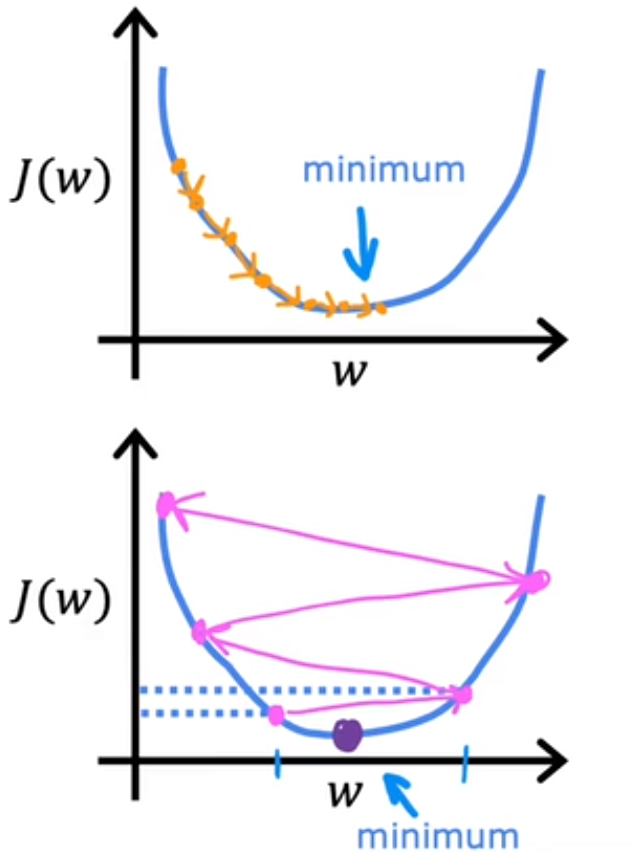
3.4 学习率的选择

适中，过大会导致过冲（overshoot），永远达不到最小值，无法收敛、发散。故在梯度下降算法中越接近局部最小值时，斜率越小，步长也越小

3.5 线性回归中的梯度下降

线性回归模型：

代价函数：

梯度下降算法：

代入后梯度函数：

3.6 批量梯度下降（"Batch" gradient descent）

定义：在梯度下降每一步中，查看所有训练样本，即计算。