自动驾驶控制算法——纯跟踪法（Pure Pursuit）

自动驾驶控制算法------纯跟踪法（Pure Pursuit）

文章目录

[自动驾驶控制算法------纯跟踪法（Pure Pursuit）](#自动驾驶控制算法——纯跟踪法（Pure Pursuit）)
一、纯跟踪法是什么？
- [1.1 定义与核心思想](#1.1 定义与核心思想)
- [1.2 纯跟踪法与其他控制器的区别](#1.2 纯跟踪法与其他控制器的区别)
- [1.3 自动驾驶中纯跟踪法的典型应用场景](#1.3 自动驾驶中纯跟踪法的典型应用场景)
二、纯跟踪法的原理
- [2.1 闭环结构总览：纯跟踪控制器如何作用于系统？](#2.1 闭环结构总览：纯跟踪控制器如何作用于系统？)
- [2.2 预瞄模型：构建几何圆弧连接模型](#2.2 预瞄模型：构建几何圆弧连接模型)
- - [2.2.1 车辆运动学模型（Kinematic Bicycle Model）](#2.2.1 车辆运动学模型（Kinematic Bicycle Model）)
  - [2.2.2 圆弧几何关系](#2.2.2 圆弧几何关系)
- [2.3 控制公式推导：纯跟踪法是怎么"转向"的？](#2.3 控制公式推导：纯跟踪法是怎么“转向”的？)
- - [2.3.1 预瞄距离 L d L_d Ld 的定义与作用](#2.3.1 预瞄距离 L d L_d Ld 的定义与作用)
  - [2.3.2 航向误差角 α \alpha α 的定义与作用](#2.3.2 航向误差角 α \alpha α 的定义与作用)
  - [2.3.3 前轮转角公式推导](#2.3.3 前轮转角公式推导)
  - [2.3.4 可视化理解](#2.3.4 可视化理解)
- [2.4 预瞄距离 L d L_d Ld 的设计原则](#2.4 预瞄距离 L d L_d Ld 的设计原则)
- - [2.4.1 固定预瞄距离](#2.4.1 固定预瞄距离)
  - [2.4.2 自适应预瞄距离](#2.4.2 自适应预瞄距离)
  - [2.4.3 预瞄距离对性能的影响](#2.4.3 预瞄距离对性能的影响)
三、纯跟踪法的控制流程
- [3.1 控制流程结构图](#3.1 控制流程结构图)
- [3.2 每一时刻的完整工作步骤](#3.2 每一时刻的完整工作步骤)
- [3.3 工作流程的优缺点总结](#3.3 工作流程的优缺点总结)
- 小结
四、纯跟踪法的参数设计与改进
- [4.1 预瞄距离 L d L_d Ld 的优化](#4.1 预瞄距离 L d L_d Ld 的优化)
- - [4.1.1 固定预瞄距离](#4.1.1 固定预瞄距离)
  - [4.1.2 自适应预瞄距离](#4.1.2 自适应预瞄距离)
  - [4.1.3 曲率相关的预瞄距离](#4.1.3 曲率相关的预瞄距离)
- [4.2 几何模型的改进](#4.2 几何模型的改进)
- - [4.2.1 考虑车辆横向偏移量](#4.2.1 考虑车辆横向偏移量)
  - [4.2.2 多点预瞄策略](#4.2.2 多点预瞄策略)
  - [4.2.3 三维路径跟踪](#4.2.3 三维路径跟踪)
- [4.3 与其他控制器的融合](#4.3 与其他控制器的融合)
- - [4.3.1 与 PID 融合](#4.3.1 与 PID 融合)
  - [4.3.2 与 MPC 融合](#4.3.2 与 MPC 融合)
  - [4.3.3 与速度规划器协同](#4.3.3 与速度规划器协同)
- [4.4 参数设计的实际建议（自动驾驶应用）](#4.4 参数设计的实际建议（自动驾驶应用）)

一、纯跟踪法是什么？

1.1 定义与核心思想

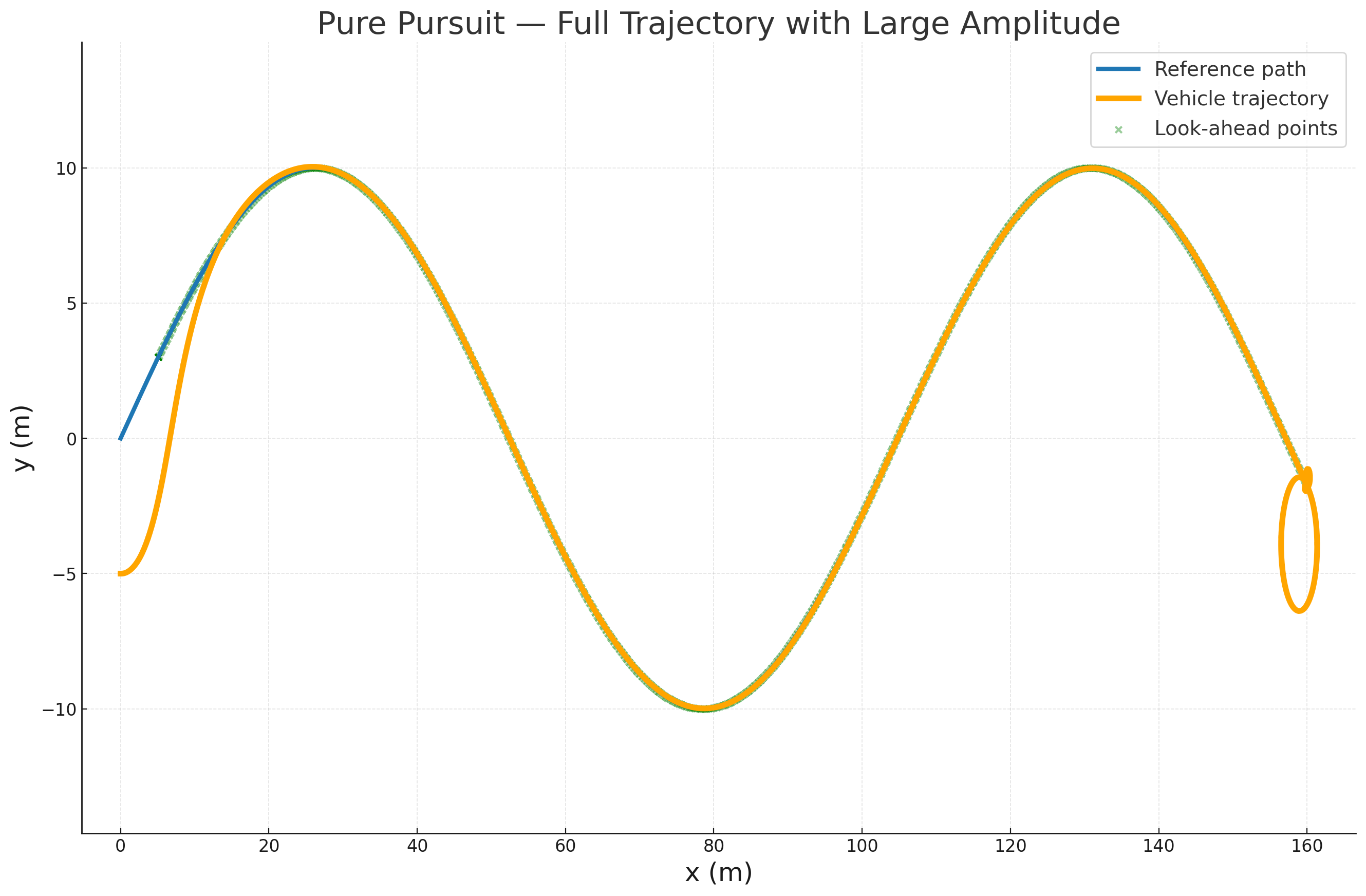
纯跟踪法（Pure Pursuit） 是一种基于几何原理的路径跟踪控制算法。其核心思想是：

在车辆当前位置沿参考路径前方一定距离处（称为"预瞄距离" LdL_dLd）选择一个目标点，车辆通过计算一个圆弧轨迹，使得前轮转向朝向该目标点，从而逐步逼近并跟随参考路径。

这一方法的本质是几何追踪（Geometric Pursuit）：

车辆并不直接修正与路径的横向误差，而是不断追逐路径上的移动目标点；
控制量（前轮转角 δ \delta δ）由车辆与该预瞄点之间的几何关系直接计算，无需显式优化求解。

核心优点：

实现简单、计算速度快、易于嵌入式部署；
对车辆动力学模型依赖较低，适合低速与中速路径跟踪。

1.2 纯跟踪法与其他控制器的区别

为了更好地理解纯跟踪法，可以将其与几种常见的路径跟踪控制方法进行对比：

方法	控制原理	优点	缺点	适用场景
纯跟踪法	基于几何圆弧拟合，追踪前方预瞄点	简单、快速、对模型依赖低	精度受预瞄距离影响大，高速急弯易偏差	低速自动驾驶、AGV、机器人导航
Stanley 方法	基于横向误差与航向误差反馈	在高速公路表现好，控制更精确	实现比纯跟踪法复杂	高速公路自动驾驶
PID 控制	基于比例、积分、微分调节误差	实现简单，易理解	参数整定敏感，抗扰性差	简单路径跟踪
MPC 控制	预测未来状态并优化控制量	精度高，可处理约束	计算量大，实时性差	高速/复杂工况的轨迹跟踪

核心差异总结：

驱动方式不同 ：纯跟踪法是几何驱动 ，Stanley/MPC 是误差驱动 或优化驱动；
计算复杂度不同：纯跟踪法几乎不做优化，计算量低；MPC 需要实时求解优化问题；
适用速度区间不同：纯跟踪法在低速场景下稳定性好，高速急转时精度不足。

1.3 自动驾驶中纯跟踪法的典型应用场景

纯跟踪法因其结构简单、易于实现，常作为自动驾驶与机器人领域的基准路径跟踪方法（baseline），具体应用包括：

轨迹跟踪控制（Trajectory Tracking）
- 在预设轨迹（如仿真路径、SLAM 建图路径）下行驶
- 低速和中速条件下效果好
车道保持与变道决策（Lane Keeping / Changing）
- 在已知车道线信息下，通过连续选取预瞄点保持在车道中心
- 适合中低速城市道路巡航
低速自主泊车
- 跟随预设泊车路径倒车或前进，路径曲率变化较小
AGV 与移动机器人导航
- 在工业园区、仓储环境中通过磁条/二维码导航的车辆路径跟随
无人小车竞赛
- 常用作入门路径跟踪算法进行快速原型开发

纯跟踪法是路径跟踪领域中最经典的几何控制算法之一，其核心是通过预瞄点+几何圆弧计算来获得转向控制量。由于实现简单、计算开销低，它被广泛应用于低速和中速自动驾驶、机器人导航等场景，并常作为控制算法性能对比的基准方法。

二、纯跟踪法的原理

2.1 闭环结构总览：纯跟踪控制器如何作用于系统？

纯跟踪法属于闭环路径跟踪控制 。在每个控制周期内，它根据车辆当前状态与参考路径的几何关系，计算出一个转向控制量（前轮转角 δ \delta δ），并作用于车辆执行器，使车辆逐步逼近目标路径。

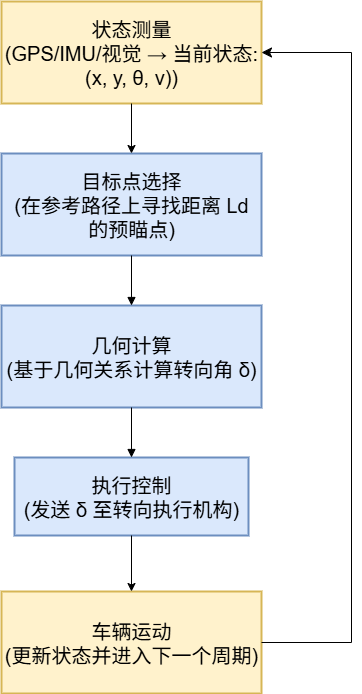
闭环信息流：

状态测量 ：车辆通过定位系统（GPS/IMU/视觉）获取当前状态 ( x , y , θ , v ) (x, y, \theta, v) (x,y,θ,v)
目标点选择 ：在参考路径上寻找与当前车辆位置相距 L d L_d Ld 的预瞄点
几何计算 ：基于车辆与目标点的几何关系，计算所需转向角 δ \delta δ
执行控制 ：将 δ \delta δ 发送给转向执行机构
车辆运动：车辆状态更新，进入下一个控制周期

2.2 预瞄模型：构建几何圆弧连接模型

2.2.1 车辆运动学模型（Kinematic Bicycle Model）

纯跟踪法通常基于单轨（自行车）运动学模型进行几何推导：

{ x ˙ = v cos ⁡ θ y ˙ = v sin ⁡ θ θ ˙ = v L tan ⁡ δ \begin{cases} \dot{x} = v \cos\theta \\ \dot{y} = v \sin\theta \\ \dot{\theta} = \frac{v}{L} \tan\delta \end{cases} ⎩ ⎨ ⎧x˙=vcosθy˙=vsinθθ˙=Lvtanδ

其中：

x , y x, y x,y：车辆质心坐标
θ \theta θ：航向角
v v v：车速
L L L：车辆轴距
δ \delta δ：前轮转角

2.2.2 圆弧几何关系

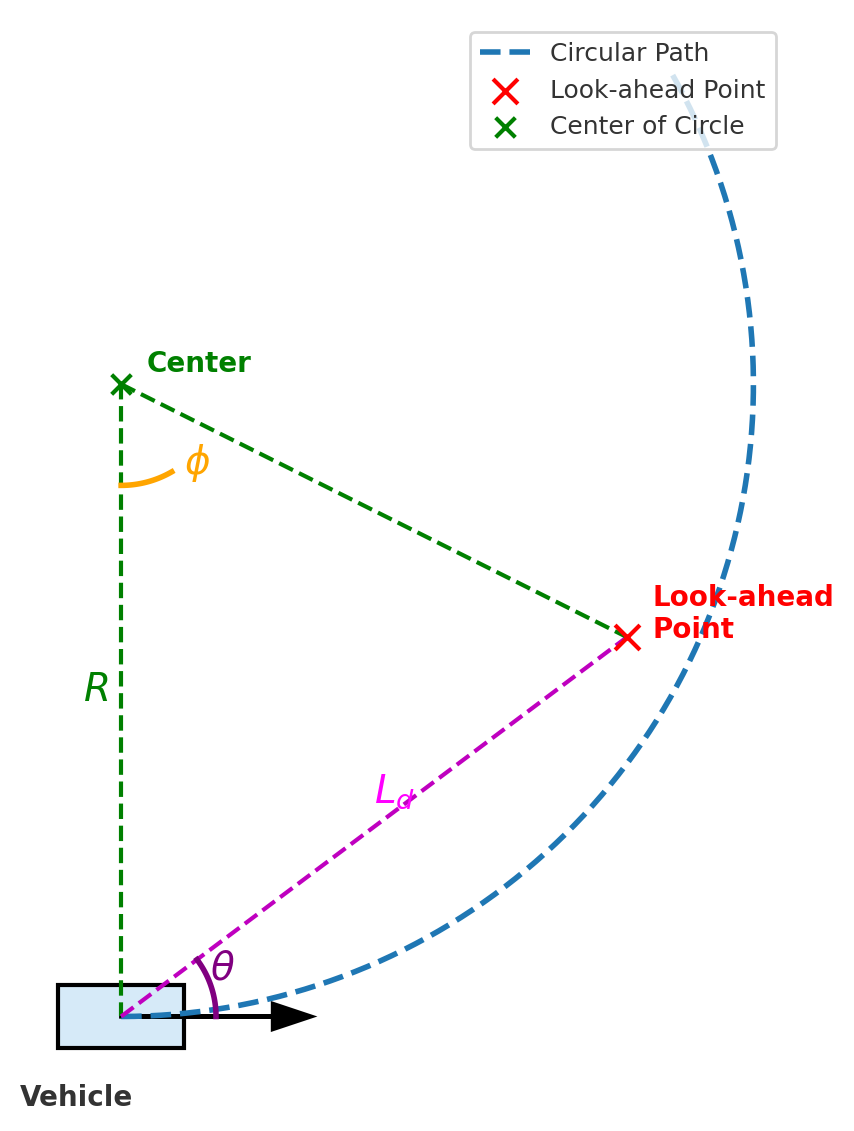
在纯跟踪法中，假设车辆当前状态与目标预瞄点之间可以用一段圆弧轨迹连接：

圆弧半径 R R R 决定转向曲率
车辆前轮转角 δ \delta δ 与半径关系为：

R = L sin ⁡ ϕ R = \frac{L}{\sin\phi} R=sinϕL

其中 ϕ \phi ϕ为前轮转动后的偏移角度

几何核心思想：车辆不断调整转向，使行驶轨迹的圆弧中心与预瞄点连成的圆弧相同。

2.3 控制公式推导：纯跟踪法是怎么"转向"的？

2.3.1 预瞄距离 L d L_d Ld 的定义与作用

定义：车辆当前位置到预瞄点沿路径的弧长距离
作用：决定车辆对未来路径的"关注程度"，影响转向灵敏度与跟踪稳定性

2.3.2 航向误差角 α \alpha α 的定义与作用

α \alpha α：车辆当前朝向与车辆到预瞄点的连线方向之间的夹角
决定了车辆需要转动多少方向才能指向预瞄点

2.3.3 前轮转角公式推导

由几何关系可得：

δ = tan ⁡ − 1 ( 2 L sin ⁡ α L d ) \delta = \tan^{-1}\left(\frac{2L \sin\alpha}{L_d}\right) δ=tan−1(Ld2Lsinα)

推导过程：

根据预瞄点坐标，计算车辆与预瞄点之间的相对位置 ( x t , y t ) (x_t, y_t) (xt,yt)
计算连线方向与车身方向的夹角 α \alpha α
根据圆弧轨迹几何关系，得到转向半径 R = L d 2 sin ⁡ α R = \frac{L_d}{2\sin\alpha} R=2sinαLd
结合单轨模型公式 δ = tan ⁡ − 1 ( L / R ) \delta = \tan^{-1}(L / R) δ=tan−1(L/R)，最终得到上述转向公式

2.3.4 可视化理解

小 L d L_d Ld：车辆更"急"地朝向预瞄点，响应快但轨迹容易抖动
大 L d L_d Ld：车辆转向平缓，轨迹更平滑但急弯跟踪不佳

2.4 预瞄距离 L d L_d Ld 的设计原则

2.4.1 固定预瞄距离

简单易实现
适合速度恒定、路线曲率变化不大的场景

2.4.2 自适应预瞄距离

根据速度自动调整：

L d = k 1 + k 2 v L_d = k_1 + k_2 v Ld=k1+k2v

高速时增大 L d L_d Ld，提升稳定性
低速时减小 L d L_d Ld，提高转向灵敏度

2.4.3 预瞄距离对性能的影响

过小：容易震荡，尤其在曲率变化快的路径
过大：急弯处跟踪误差大，可能"切弯"

纯跟踪法的控制核心是预瞄点选择 + 几何计算转向角。它通过单轨运动学模型和圆弧几何关系，将路径跟踪问题简化为一个直接计算公式，计算量低、实时性好，但其性能高度依赖预瞄距离的设计。

三、纯跟踪法的控制流程

3.1 控制流程结构图

在纯跟踪法中，控制器每个周期会接收车辆当前状态与参考路径数据，选择目标预瞄点，并基于几何关系计算前轮转角，最终驱动车辆执行。其闭环控制结构可用下图表示：

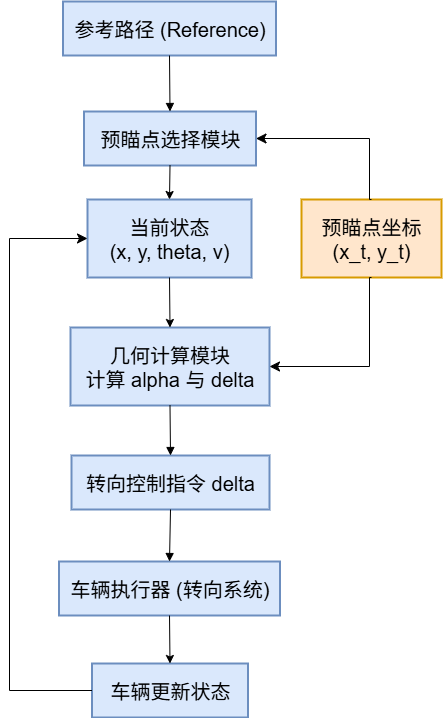
3.2 每一时刻的完整工作步骤

在控制时刻 k k k，纯跟踪法的计算与执行过程可以分为以下 5 步：

Step 1：获取车辆当前状态

通过 GPS、IMU、里程计等传感器获取位置 ( x k , y k ) (x_k, y_k) (xk,yk)、航向角 θ k \theta_k θk、车速 v k v_k vk
状态信息为预瞄点选择和几何计算提供基础

Step 2：沿参考路径寻找预瞄点

在路径点集合中找到与车辆当前位置沿路径方向距离为 L d L_d Ld 的目标点
若路径是离散点序列，则可通过累计弧长寻找最近匹配点

Step 3：计算航向误差角 α k \alpha_k αk

根据车辆位置和目标点坐标，计算目标点方向与车辆当前航向之间的夹角
α k = atan2 ( y t − y k , x t − x k ) − θ k \alpha_k = \text{atan2}(y_t - y_k, x_t - x_k) - \theta_k αk=atan2(yt−yk,xt−xk)−θk

Step 4：几何公式求解前轮转角 δ k \delta_k δk

使用公式

δ k = tan ⁡ − 1 ( 2 L sin ⁡ α k L d ) \delta_k = \tan^{-1} \left( \frac{2L \sin\alpha_k}{L_d} \right) δk=tan−1(Ld2Lsinαk)

L L L 为车辆轴距

Step 5：发送转向控制指令

将 δ k \delta_k δk 发送至车辆转向执行机构
车辆状态更新后进入下一时刻 k + 1 k+1 k+1，重复整个流程

3.3 工作流程的优缺点总结

优点

实现简单：核心是几何计算，无需求解优化问题
计算速度快：适合实时性要求高的嵌入式平台
对车辆模型依赖低 ：不需要完整的动力学参数，仅需轴距 L L L
调参直观 ：主要调节预瞄距离 L d L_d Ld

缺点

性能依赖预瞄距离 ：固定 L d L_d Ld 在高速或急弯下效果可能不佳
忽略动力学约束：高速转弯时可能出现不可实现的转角指令
对急弯敏感：预瞄点可能位于车辆可达范围之外，导致跟踪误差增大

小结

纯跟踪法的控制流程以**"测量状态 → 选取预瞄点 → 几何计算转角 → 执行转向"**为核心循环，优点是快速简洁，缺点是缺乏对动力学约束和速度适应性的考虑，因此在实际应用中，常需结合速度自适应预瞄距离或与其他控制器（如 PID、MPC）融合以提高精度与稳定性。

四、纯跟踪法的参数设计与改进

4.1 预瞄距离 L d L_d Ld 的优化

预瞄距离是纯跟踪法中最核心的调节参数，直接影响控制性能、稳定性和跟踪精度。

4.1.1 固定预瞄距离

定义：在整个行驶过程中保持 L d L_d Ld 不变
优点：实现简单，计算稳定
缺点：无法兼顾不同速度和曲率条件下的跟踪需求
适用场景：低速、曲率变化小的路径（如仓储 AGV）

4.1.2 自适应预瞄距离

为了兼顾低速灵敏度与高速稳定性，常采用速度相关的预瞄距离设计：

L d = k 1 + k 2 v L_d = k_1 + k_2 v Ld=k1+k2v

其中：

v v v：当前车辆速度
k 1 , k 2 k_1, k_2 k1,k2：调节系数
作用：高速时增大 L d L_d Ld（稳定性提升），低速时减小 L d L_d Ld（灵敏度提升）

4.1.3 曲率相关的预瞄距离

根据参考路径的局部曲率 κ \kappa κ 调节 L d L_d Ld：

L d = min ⁡ ( L max ⁡ , max ⁡ ( L min ⁡ , f ( κ ) ) ) L_d = \min(L_{\max}, \max(L_{\min}, f(\kappa))) Ld=min(Lmax,max(Lmin,f(κ)))

在急弯（ κ \kappa κ 大）时减小 L d L_d Ld，在直道时增大 L d L_d Ld

4.2 几何模型的改进

虽然传统纯跟踪法基于单轨几何模型即可实现路径跟踪，但在某些场景中可进行扩展：

4.2.1 考虑车辆横向偏移量

在几何计算中引入横向误差补偿项，使转向角不仅指向预瞄点，还补偿横向距离
类似 Stanley 方法的思想，可增强曲率变化处的跟踪精度

4.2.2 多点预瞄策略

同时选择多个预瞄点（短距+长距），综合计算转向角：
- 短距点保证曲率响应
- 长距点保证路径平滑性
通过加权平均得到最终转向角：

δ = w 1 δ short + w 2 δ long \delta = w_1 \delta_{\text{short}} + w_2 \delta_{\text{long}} δ=w1δshort+w2δlong

4.2.3 三维路径跟踪

针对无人机、无人船等需要在三维空间跟踪路径的场景，将预瞄点选择和几何计算扩展至三维坐标系
考虑俯仰角、滚转角等控制变量

4.3 与其他控制器的融合

在高速或复杂路况下，纯跟踪法单独使用可能不足以满足精度和稳定性要求，因此可与其他控制方法融合：

4.3.1 与 PID 融合

纯跟踪法输出的转向角作为基准值
PID 控制器修正横向误差，补偿纯跟踪法对急弯的响应不足

4.3.2 与 MPC 融合

MPC 预测未来路径，并将预测的最优转向序列的首个值作为纯跟踪法的预瞄目标
纯跟踪法提供快速几何计算，MPC 提供预测优化能力

4.3.3 与速度规划器协同

根据路径曲率和道路条件，动态调整车速，使预瞄距离和速度匹配
例如：急弯自动减速，直道自动加速

4.4 参数设计的实际建议（自动驾驶应用）

预瞄距离：建议在低速（<10 km/h）时取 2--3 m，高速时取 10--15 m，并随速度连续调整
调参顺序 ：先固定 k 1 k_1 k1 调整 k 2 k_2 k2，保证高速稳定性，再回调 k 1 k_1 k1 提升低速灵敏度
曲率适配 ：在急弯处通过路径曲率自适应调整 L d L_d Ld
横向偏差补偿：在直道稳定性良好的情况下，可加入横向误差反馈提升精度