深度强化学习(5_5):AlphaGo_哔哩哔哩_bilibili
蒙特卡洛 Monte Carlo_哔哩哔哩_bilibili
目录
[0. 主要步骤:](#0. 主要步骤:)
[1. Initialize by Behavior Cloning 行为克隆初始化](#1. Initialize by Behavior Cloning 行为克隆初始化)
[2. Train Policy Network Using Policy Gradient 训练策略网络](#2. Train Policy Network Using Policy Gradient 训练策略网络)
[3. Train the Value Network 评估盘面的价值网络](#3. Train the Value Network 评估盘面的价值网络)
[4.Monte Carlo Tree Search蒙特卡洛树搜索(MCST)](#4.Monte Carlo Tree Search蒙特卡洛树搜索(MCST))
[5. AlphaGo Zero 升级版](#5. AlphaGo Zero 升级版)
[6. Monte Carlo 蒙特卡洛思想](#6. Monte Carlo 蒙特卡洛思想)
state状态 19*19的位置 每个位置若只用黑白棋两种 就是19*19*2的tensor
但为了效果更好 每个位置在专业棋手指导下设定 48个特征。
所以state 可以用19*19*48的tensor表示
action行动A 可以在361个格子选择 每个格子标号1-361 即选择一个数字,
象棋AI深蓝通过暴力搜索战胜职业选手,但围棋盘面可能性更多,无法仅依靠搜索。
0. 主要步骤:
一、训练部分(Training in 3 steps)
-
初始化策略网络(Policy Network)------行为克隆 (Behavior Cloning) 模仿人类
-
先用 人类棋谱数据来训练策略网络。
-
这是一个监督学习过程:输入棋盘状态,预测人类棋手的下一步。
-
目的:让 AlphaGo 一开始就能下出"像人类一样"的合理棋。模仿人类高水平棋手。
-
-
训练策略网络 (Policy Gradient)下的更好
-
将训练好的策略网络拿来互相对弈(自我博弈)。
-
使用 Policy Gradient**(策略梯度)方法**更新网络。
-
这样 AlphaGo 不仅模仿人类,还能通过自我博弈发现超越人类经验的走法。
-
-
训练价值网络 (Value Network)评估盘面
-
在有了较强的策略网络 后,用它产生大量对局数据。
-
用这些数据来训练一个 价值网络(Value Network),它能直接预测从某个棋盘状态到最后输赢的概率。
-
这样,AlphaGo 就能评估局面,而不仅仅是预测下一步棋。
-
二、执行部分(Execution: actually play Go games)
-
在实际对弈时,AlphaGo 并不是直接用策略网络一步步走,而是:
结合策略网络和价值网络做 Monte Carlo Tree Search (蒙特卡洛树搜索)。-
策略网络:在搜索中提供"走子方向"的先验概率(告诉 MCTS 哪些棋更值得考虑)。
-
价值网络:在搜索中 评估 某局面价值时参考(不用完全模拟到终局)。
-
MCTS:通过不断模拟和搜索,选择最优落子。
-
1. Initialize by Behavior Cloning 行为克隆初始化
如果是随机初始化直接训练策略网络的话 因为情况太多导致难以摸索好策略,难以选择合理的action。(就像初学者会学一些棋谱 定式之类)
这个阶段是一种模仿学习 有监督的(不是强化学习 没有reward)
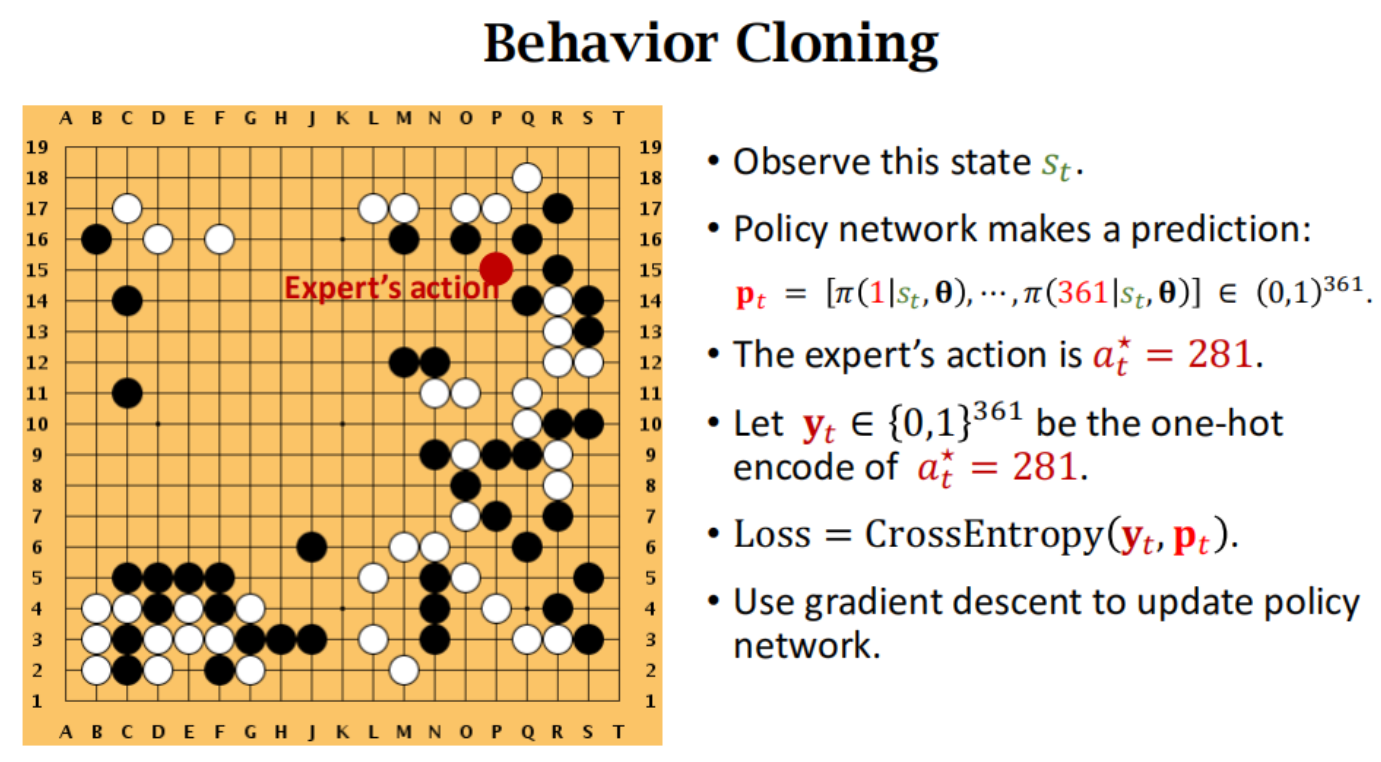
人类玩家下一个位置 作为ground truth (也是其他位置为0 只有一个位置为1的独热编码)
policy network进行预测下一个位置 每个位置为当前状态的条件概率 值,就可以算交叉熵损失。
就类似多分类问题,这一步棋分到每一个格子的概率(人类的走法作为标签)
最大的问题 :如果一个state在训练数据里没有 之前没见过这个盘面 那给出的走法就会比较差。
依赖大量的高质量的专家数据 ;并且不具备未知环境探索能力。
2. Train Policy Network Using Policy Gradient 训练策略网络
两个策略网络进行博弈,一个叫做Player,另一个叫做Opponent。
Player是agent,由策略网络来控制的,用的是策略网络最新 的模型参数(每下完一局围棋把胜负作为奖励,靠奖励来更新player的参数)
Opponent相当于environment,它负责陪玩,也用策略网络来控制,但是opponent的参数无需学习,随机从旧的策略网络的参数中随机选择一个即可。
(最新的Player 力争打败随机之前的自己)
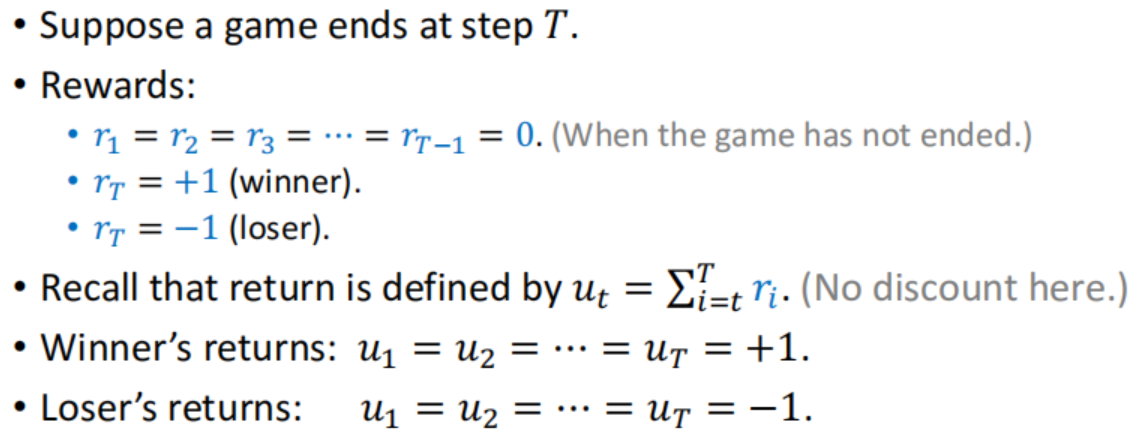
假设下了T步 最后一步知道赢输±1;累加到之前 就是如果赢了每步u=1 输了则每步u=-1
也就是最后结算 赢了就每一步都是好棋 输了就每一步都是坏棋,中间不做区分。
训练时 就像policy network中的 Reinforce 算法 先开一把 得到每步u 从后往前策略梯度。

3. Train the Value Network 评估盘面的价值网络
不同于actor-critic 这是先训练策略网络 在policy的帮助下训练价值网络。
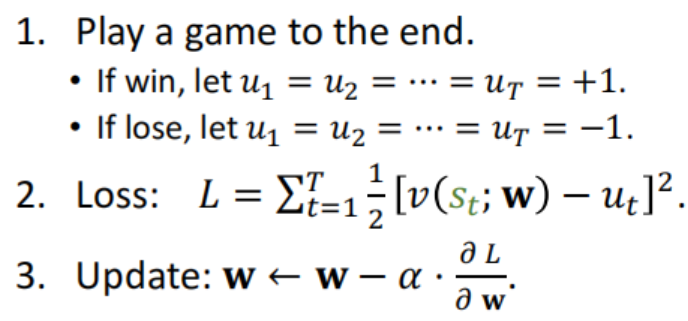
进行一个回归问题 对当前盘面s应该打多少分? 还是两个策略网络开一把 再反过来更新。
开一把得到参考值:赢得话依次所有盘面都标签+1分 输的话所有盘面标签为-1分
小结:策略/价值网络 都是根据开一把 每一步/盘面 赢 得对应都标签**+1** 输 的对应都标签**-1**
4.Monte Carlo Tree Search蒙特卡洛树搜索(MCST)
人类高手下棋:几个貌似可行的走法 我这么走之后 对手怎么走 往未来计算看很多步数
(预见未来)假设我能看到所有未来的变化情况 就像延伸到最后的树一样,
相当于我每次都可以做应对对手的 全局绝对最优策略 那就一定能赢。就像博弈中min-max。
当下盘面的选择,就是想要得到每个动作 最接近全局盘面下的 最合理的"综合得分"
一直重复以下四步 建立出下面这样的树:
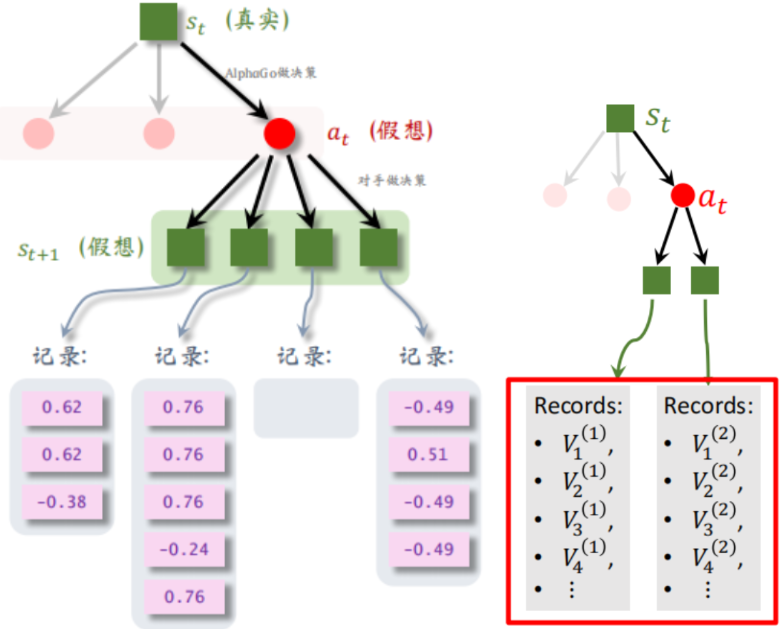
第一步. 选一个动作a探索(对它后续进一步搜索)

盘面上几百个空位 但每次实际只有个别空位是比较合理的。 每次探索score最高的。
这个 score反映探索价值 第二项的π 是策略网络 打的分,Q(a) 为后续MCTS第四步回溯打的分,
一个action 探索次数N(a)高了就会使得 第二项分数变小。
每次初始化 Q和N都为0 使得一开始π为主 后来Q为主。

第二步. expansion 在a_t后面拓展 使用策略网络 sample对手的走法 得到s_t+1

第三步. 衡量s_t+1好坏 用策略网络 模拟双方一直往后下 得到输赢r
将输赢r 和价值网络v 结果取平均记录在 s_t+1。
(网络交替落子,要走上百步, 导致第三步成为 MCTS 的瓶颈。用小的策略网络代替大的策略网络,可大幅加速 MCTS。)

第四步. 回溯backup 由于这种模拟会重复上万次 每次会在s_t+1得到一个分数记录
可以对a_t 下的所有s_t+1的所有记录的结果取平均作为Q(a)
总结上面的 MCST模拟建树求动作a 的Q和N值过程。
第一,selection,根据动作的分数(Q和N加权),选出分数最高的动作。
第二,expansion,用策略网络来模拟对手的动作a_t,产生新的状态s_t+1。
第三,evaluation,通过自我博弈r 和价值网络v 这两个途径算出两个分数,记录它们的平均值。
第四,backup,记录第三步算出来的分数,把a下面的所有分数取平均值更新Q。
AlphaGo每走一步,都要进行成千上万次模拟。每次模拟都要重复以上四步。

最后根据a的探索次数N 选取(探索次数多 说明曾多次score很高 曾多次值得探索)
选N最大而不是 Q最大的更鲁棒一些(多次受青睐的节点 Q最大可能没探索过几次但平均值高 要想多次探索 说明其之前Q也经常很高)
5. AlphaGo Zero 升级版
AlphaGo Zero完胜AlphaGo,区别有两个:
1.没有用behavior cloning 反而效果更好(一方面因为 人类哪怕大师棋手 走的棋还是局部的对于全局并不一定很优 这些数据可能反而对训练有害)
但是behavior cloning 在别的领域 比如手术、无人驾驶还是非常重要的,因为clone是不需要结果作为reward的(手术失败或者无人驾驶故障作为reward 代价太大了)
2.在训练策略网络的时候使用MCTS。
参考值从独热向量 的只有一点为1,到正则化的蒙特卡洛模拟 这步被探索的次数N,再用交叉熵。

6. Monte Carlo 蒙特卡洛思想
通过随机抽样来近似解决问题(随机算法)
1.计算阴影部分面积S1 可以在大面积S均匀投点n次 m次在S1 则 S1 / S = m / n
2.计算f(x) 在[a,b] 近似定积分 在[a,b]采样n个f(x) 取平均值乘以(b-a)
3.计算f(x)期望 定积分乘上p(x)概率的变形,按照p(x)概率采样得到f(x) 再取平均值
这样动态求均值 为了减少内存还可以这样操作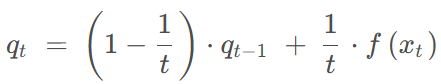
重点:应用在随机梯度 算法SGD Stochastic Gradient Descent上
机器学习 强化学习的训练任务 很多是拟合 并 最小化期望损失 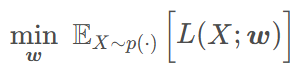
训练减少损失 就对w求梯度 ;但求这个期望的梯度 比较复杂 可以对这个期望做蒙特卡洛近似
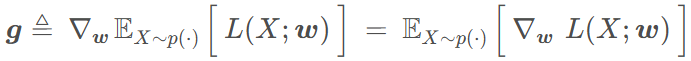
期望梯度 在概率p(x)下采样 n个值算n个梯度,并把这n个梯度的平均值 作为随机梯度g'更新w