初识数据结构——Map和Set：哈希表与二叉搜索树的魔法对决

想不明白的过度思考者2025-08-23 12:14



数据结构专栏 ⬅(click)

大家好！我是你们的老朋友------想不明白的过度思考者！今天我们要一起探索Java中两个神奇的数据结构：Map和Set！准备好了吗？让我们开始这场魔法之旅吧！🎩

🎯 先来点开胃菜：二叉搜索树（BST）

🌳 什么是二叉搜索树？

想象一下，你有一棵神奇的树，左边的果子都比树根小，右边的果子都比树根大！这就是我们的二叉搜索树！

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树
java 复制代码 
package Tree;

//表示树的节点
class Node {
    public int key;
    public Node left;
    public Node right;
    public Node(int key) {
        this.key = key;
    }

    @Override
    public String toString() {
        return "Node{" +
                "key=" + key +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}

public class BinarySearchTree {
   private Node root = null;


   //把新的元素插入到树中
   public void insert(int key) {
        //如果当前是空树，那就直接用root指向新节点即可
       Node newNode = new Node(key);
       if (root == null) {
           root = newNode;
       }
       // 如果是普通的树，需要找到哦插入位置，再去进行插入
       //cur用来找待插入元素的位置
       //parent记录cur的父元素
       Node cur = root;
       Node parent = null;
       while (cur != null) {
           if(key<cur.key) {
               //往左找
               parent = cur;
               cur = cur.left;

           }else if(key>cur.key) {
               //往右找
               parent = cur;
               cur = cur.right;

           }else {
               //对于相等的情况，存在不同的解决方式
               //当前不允许重复key存在，并且是Set只保存key，直接return
               return;
           }
       }
       //通过上述循环最终得到的结果就是cur为空
       //此时的parent就是叶子节点，也就是新插入元素的父亲，此时就是要把newNode插入到parent的子节点上
       //新节点，应该在parent的左子树还是右子树呢??直接比较大小
       if (key> parent.key){
           parent.right = newNode;
       }else {
           parent.left = newNode;
       }
   }

   public void remove(int key) {
       if (root == null) {
           return;
       }
       //查找要删除节点的位置，记录其父节点
       Node cur = root;
       Node parent = null;
       while (cur != null) {
           if(key<cur.key) {
               parent = cur;
               cur = cur.left;
           }else if(key>cur.key) {
               parent = cur;
               cur = cur.right;
           }else {
               //找到了
               removeNode(parent, cur);
               return;
           }
       }

   }


   private void removeNode(Node parent, Node cur) {
       //具体删除节点要考虑四种情况
       //1.没有子树
       if(cur.right == null && cur.left == null) {
           //1.1如果cur就是root，需要对root进行调整
           if(cur == root) {
               //说明整棵树只有root一个节点，直接把root设置为空
               root = null;
           }
           //1.2如果cur不是root，同时cur是parent的左子树
           if (cur == parent.left) {
               parent.left = null;
               return;
           }
           //1.3如果cur不是root，同时cur是parent的右子树
            if (cur == parent.right) {
                parent.right = null;
                return;
            }
            //稳妥起见加个return
           return;
       }
       //2.只有左子树
       if(cur.left != null && cur.right == null) {
            //2.1cur为root
           if(cur == root){
               root = cur.left;
               return;
           }
           //2.2cur不为root，且cur是parent的左子树
           if (cur == parent.left) {
               parent.left = cur.left;
               return;
           }
           //2.3cur不为root，且cur是parent的右子树
            if (cur == parent.right) {
                parent.right = cur.left;
                return;
            }

       }

       //3.只有右子树
       if(cur.left == null && cur.right != null) {
           //3.1只有root
           if(cur == root){
               root = cur.right;
               return;
           }
           //3.2cur不是root，且cur是parent的左子树
           if (cur == parent.left) {
               parent.left = cur.right;
               return;
           }
           //3.3cur不是root，且cur是parent的右子树
           if (cur == parent.right) {
               parent.right = cur.right;
               return;
           }

       }
       //4.左右都有子树
       if(cur.left != null && cur.right != null) {
           // 这种情况下，不需要考虑 cur 是不是 root的情况，并没有真正的删除 cur指向的节点，即使 cur 是 root，也无需修改 root 的指向
           //因为实际删除的是"替罪羊节点"
           //4.1首先需要找到右子树中的最小值 =>替罪羊,
           //后续要删除替罪羊，也顺便把替罪羊的父亲，记录一下.
           Node goat = cur.right;
           Node goatParent= cur;
           while (goat.left != null) {
               goatParent = goat;
               goat = goat.left;
           }
           //循环结束后。goat指向的就是cur右子树的最左侧元素
           //4.2移花接木，把替罪羊节点的值复制到cur节点中
           cur.key = goat.key;
           //4.3真正删除goat节点，因为goat是没有左子树的，让goatParent直接连上goat的右子树即可
           // 即使goat的右子树也是空也不影响
            if(goat == goatParent.left){
                goatParent.left = goat.right;
            }else {
                goatParent.right = goat.right;
            }
       }
   }


   //查找key是否在树中，如果存在则返回对应节点位置，如果不存在则返回null
    private Node find(int key) {
       if (root == null) {
           return null;
       }
       Node cur = root;
       while (cur != null) {
           if(key<cur.key) {
               cur = cur.left;
           }
           else if(key>cur.key) {
               cur = cur.right;
           }else {
               //相等，找到了
               return cur;
           }
       }
       return null;
    }


   //先序遍历
   private static void preOrder(Node root) {
       if (root == null) {
           return;
       }

       System.out.print(root.key + " ");
       preOrder(root.left);
       preOrder(root.right);
   }

   //中序遍历
    private static void inOrder(Node root) {
        if (root == null) {
            return;
        }
       inOrder(root.left);
       System.out.print(root.key + " ");
        inOrder(root.right);
    }



   public void print(){
       //先打印先序遍历
       System.out.println("先序遍历结果：");
       preOrder(root);
       System.out.println();
       //在打印中序遍历
       System.out.println("中序遍历结果：");
       inOrder(root);
       //有了先序和中序就能够画出树的结构
   }


    public static void main(String[] args) {
       int[] arr = {1, 3, 2, 6, 5, 7, 8, 9, 10, 0};

       //BinarySearchTree也总被缩写成BST
        BinarySearchTree tree = new BinarySearchTree();
        //循环插入
        for(int key: arr){
            tree.insert(key);
        }
        tree.print();
        System.out.println();
        System.out.println(tree.find(7));
    }
}

🎭 BST的表演时刻

操作 最佳情况（完全二叉树） 最差情况（单支树）
查找 O(logN) O(N)
插入 O(logN) O(N)
删除 O(logN) O(N)

💡 小贴士：Java中的TreeMap和TreeSet就是用红黑树（BST的升级版）实现的哦！

🎩 主角登场：Map和Set

🗺️ Map：你的万能字典

Map就像你的通讯录，名字（Key）对应电话（Value），而且名字不能重复！

java 复制代码 
Map<String, String> heroNicknames = new HashMap<>();
heroNicknames.put("林冲", "豹子头");
heroNicknames.put("李逵", "黑旋风");
heroNicknames.put("宋江", "及时雨");

// 获取外号
System.out.println(heroNicknames.get("林冲"));  // 输出：豹子头

// 遍历所有英雄
for (Map.Entry<String, String> entry : heroNicknames.entrySet()) {
    System.out.println(entry.getKey() + "的外号是：" + entry.getValue());
}
  • Tip ：使用put方法时：
    若key不同 ，value相同 则新增键值对
    若key相同 ，value不同则为修改对应的value

🎭 Map的两种实现对比

特性 TreeMap（红黑树） HashMap（哈希表）
底层结构 红黑树 哈希桶
时间复杂度 O(logN) O(1)
是否有序 Key有序 无序
允许null Key不能为null Key和Value都可以为null

🎪 Set：独一无二的马戏团

Set就像一个不允许重复演员的马戏团，每个演员都是独一无二的！

java 复制代码 
Set<String> fruitSet = new HashSet<>();
fruitSet.add("苹果");
fruitSet.add("香蕉");
fruitSet.add("橙子");
fruitSet.add("苹果");  // 这个不会被添加进去

System.out.println(fruitSet.contains("香蕉"));  // 输出：true
System.out.println(fruitSet.size());          // 输出：3

🎭 Set的两种实现对比

特性 TreeSet（红黑树） HashSet（哈希表）
底层结构 红黑树 哈希桶
时间复杂度 O(logN) O(1)
是否有序 Key有序 无序
允许null 不允许 允许

🔮 哈希表：数据结构的魔法帽

🎩 哈希函数：魔法咒语

哈希函数就像把名字变成数字的咒语：

java 复制代码 
int hashCode = "魔法".hashCode();  // 返回一个魔法数字

⚡ 哈希冲突：当两个咒语撞车了

当不同的Key计算出相同的哈希值，就发生了冲突！我们有几种解决办法：

  1. 开放地址法（线性探测/二次探测）

    • 线性探测：h(key) = (h(key) + i) % size
    • 二次探测：h(key) = (h(key) + i²) % size

  2. 链地址法（哈希桶）

    • 每个位置放一个链表，冲突的元素都挂在链表上

🌟 哈希桶实现：我们的魔法实验室

java 复制代码 
public class HashBucket {
    static class Node {
        int key, value;
        Node next;
        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }
    
    private Node[] array;
    private int size;
    private static final double LOAD_FACTOR = 0.75;
    
    public HashBucket() {
        array = new Node[8];
        size = 0;
    }
    
    public int put(int key, int value) {
        int index = key % array.length;
        
        // 查找key是否已存在
        for (Node cur = array[index]; cur != null; cur = cur.next) {
            if (key == cur.key) {
                int oldValue = cur.value;
                cur.value = value;
                return oldValue;
            }
        }
        
        // 插入新节点
        Node node = new Node(key, value);
        node.next = array[index];
        array[index] = node;
        size++;
        
        // 检查是否需要扩容
        if ((double)size / array.length >= LOAD_FACTOR) {
            resize();
        }
        
        return -1;
    }
    
    private void resize() {
        Node[] newArray = new Node[array.length * 2];
        for (int i = 0; i < array.length; i++) {
            Node next;
            for (Node cur = array[i]; cur != null; cur = next) {
                next = cur.next;
                int index = cur.key % newArray.length;
                cur.next = newArray[index];
                newArray[index] = cur;
            }
        }
        array = newArray;
    }
    
    public int get(int key) {
        int index = key % array.length;
        for (Node cur = array[index]; cur != null; cur = cur.next) {
            if (key == cur.key) return cur.value;
        }
        return -1;
    }
}

📊 哈希表性能分析

因素 影响
哈希函数设计 决定冲突率高低
负载因子 通常控制在0.75以下
冲突解决方法 影响查找效率和内存使用
扩容机制 影响性能和内存使用的平衡

🎯 实战演练：OJ题目解析

1. 只出现一次的数字

题目：给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

魔法解法：使用异或运算的特性！

java 复制代码 
public int singleNumber(int[] nums) {
    int result = 0;
    for (int num : nums) {
        result ^= num;
    }
    return result;
}

2. 宝石与石头

题目：给定字符串J代表宝石的类型，S代表你拥有的石头。你想知道你拥有的石头中有多少是宝石。

魔法解法：使用HashSet！

java 复制代码 
public int numJewelsInStones(String J, String S) {
    Set<Character> jewels = new HashSet<>();
    for (char c : J.toCharArray()) {
        jewels.add(c);
    }
    
    int count = 0;
    for (char c : S.toCharArray()) {
        if (jewels.contains(c)) count++;
    }
    return count;
}

🎓 知识总结：思维导图

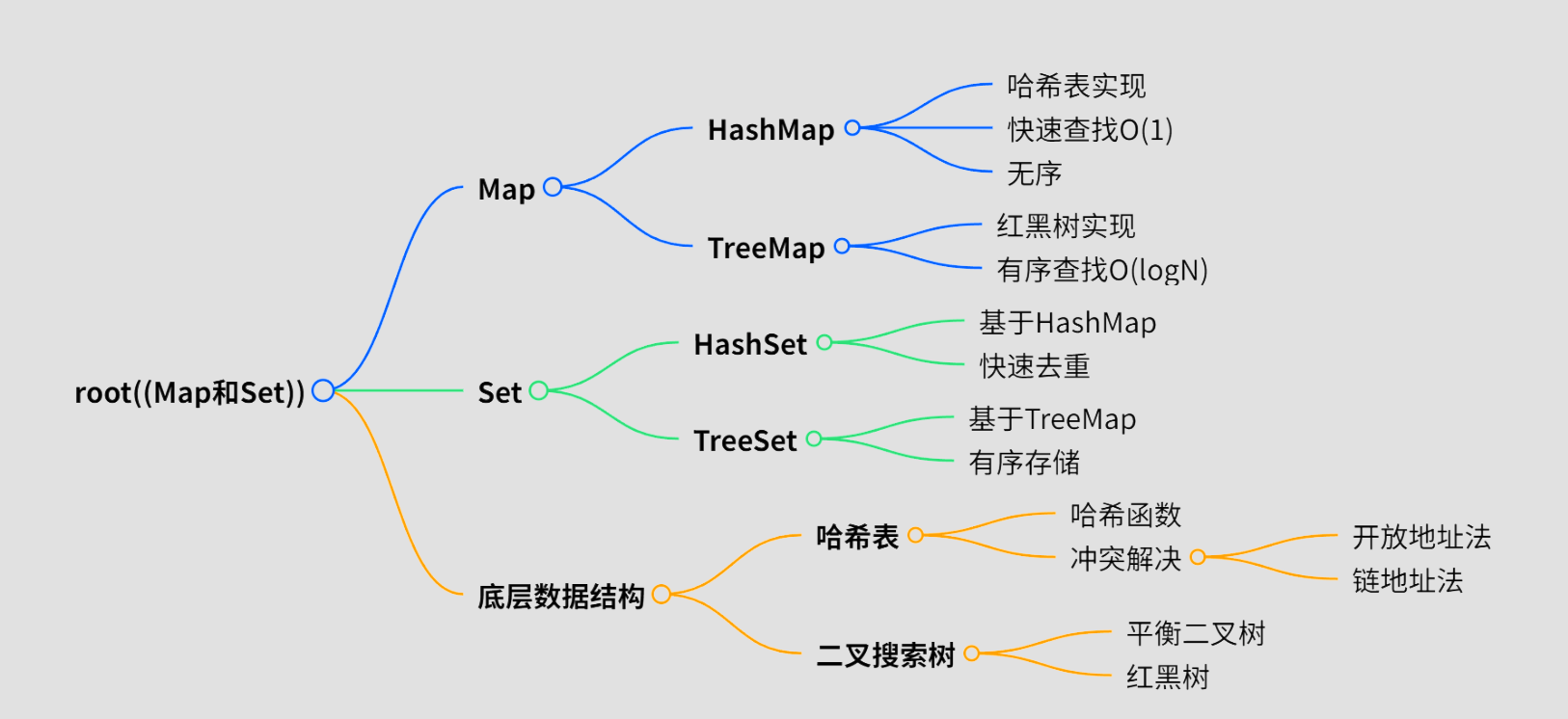
🎉 结语：选择你的魔法武器

今天我们一起探索了Map和Set的魔法世界，从二叉搜索树到哈希表，从TreeMap到HashMap，每个数据结构都有它独特的魔法特性！

记住：

  • 需要快速查找？选HashMap/HashSet！
  • 需要有序存储？选TreeMap/TreeSet！
  • 遇到哈希冲突？试试链地址法！

希望这篇博客能像魔法一样帮助你理解这些数据结构！

相关推荐
Y4090011 小时前
Java算法之排序
java·数据结构·笔记·算法
艾莉丝努力练剑3 小时前
【C语言16天强化训练】从基础入门到进阶：Day 6
c语言·数据结构·学习·算法
快去睡觉~4 小时前
力扣1005:k次取反后最大化的数组和
数据结构·算法·leetcode
天意生信云4 小时前
生信分析自学攻略 | R语言数据筛选和修改
数据结构·经验分享·r语言
月盈缺4 小时前
学习嵌入式第二十三天——数据结构——栈
数据结构·学习
fs哆哆16 小时前
在VB.net中一维数组，与VBA有什么区别
java·开发语言·数据结构·算法·.net
gihigo199820 小时前
matlab多目标优化差分进化算法
数据结构·算法
JNU freshman1 天前
算法 之 拓 扑 排 序
数据结构·算法
小指纹1 天前
河南萌新联赛2025第（六）场：郑州大学
java·开发语言·数据结构·c++·算法
热门推荐
01UV安装并设置国内源02KGG转MP3工具|非KGM文件|解密音频03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接05Claude Code VSCode集成开发指南：AI编程助手完整配置06DeepSeek更新！速览DeepSeek V3.1新特性07【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南092025最新国内服务器可用docker源仓库地址大全（2025年8月更新）10【踩坑笔记】50系显卡适配的 PyTorch 安装