图论——Floyd算法

图论------Floyd算法

文章目录

图论------Floyd算法
算法解释
- 初始化
- 核心代码
经典题目
- 代码

图论的这几个算法都是用来求最短路的，回顾一下之前的两个算法：Djikstra是用来求单源无负权值最短路的，Bellman-Ford是用来求有负权值的最短路。而本算法是求全源最短路的，也可以处理有负权值的情况。那么问题就来了，既然能求全源最短路还能处理负权值为啥还要学前两个。既然功能强大肯定是要付出一定代价的：时间复杂度很高。Djikstra经过优化可以达到 O ( m l o g ( n ) ) O(mlog(n)) O(mlog(n))，Bellman-Ford经过优化之后（也就是SPFA）的时间复杂度不是特别固定，但是较坏的情况也不过是 O(VE) （其中 k 是小常数，E 为图的边数）。而本算法时间复杂度来到了 O ( n 3 ) O(n^{3} ) O(n3)！下面用这张表来对比一下：

核心要素	Dijkstra 算法	SPFA 算法（Shortest Path Faster Algorithm）	Floyd 算法
核心作用	求单源最短路径（从一个起点到所有其他顶点）	求单源最短路径（Bellman-Ford 算法优化）	求多源最短路径（所有顶点对之间的最短路径）
适用图类型	边权非负的有向 / 无向图	边权可正可负、但无负权回路的图；可检测负权回路	边权可正可负、但无负权回路的图；可检测负权回路
时间复杂度	朴素版：O (V²)，堆优化版：O ((V+E) logV)	平均情况：O (kE)（k 为小常数）；最坏情况：O (V・E)	固定：O (V³)（V 为顶点数，E 为边数）
空间复杂度	朴素版：O (V)；堆优化版：O (V+E)（邻接表 + 堆）	O (V+E)（邻接表 + 队列）	原始版：O (V²)；优化版（滚动数组）：O (V)
关键特点	1. 无法处理负权边； 2. 堆优化后稀疏图效率高	1. 可处理负权边，支持负权回路检测； 2. 最坏情况退化	1. 实现简单（三重循环）； 2. 时间复杂度高，仅适合小规模图

算法解释

本算法的大致思路是设置一个变量 k k k，外层 k k k从 1 − n 1-n 1−n，每次只能经过此点。内层则是遍历 i i i和 j j j表示从 i i i到 j j j，用动态规划递推一遍，最后每条路经过任何一个点的路径都被遍历到了，并且在遍历过程中都取了最小值。

初始化

cpp 复制代码

for(int i=1; i<=n; i++)
{
	cin >> u >> v > w;
	dp[u][v]=w;//存最开始的距离（初始化）
	dp[v][u]=w;
}

核心代码

cpp 复制代码

fill(dp,dp+N*N,INF);
for(int k=1; k<=n; k++)
	for(int i=1; i<=n; i++)
		for(int j=1; j<=n; j++)
			dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);

经过这轮递推所有点对点的最短路径都被求出来了，到查询的时候每次 O ( 1 ) O(1) O(1)查询就行了。下面是整个递推过程的图示：

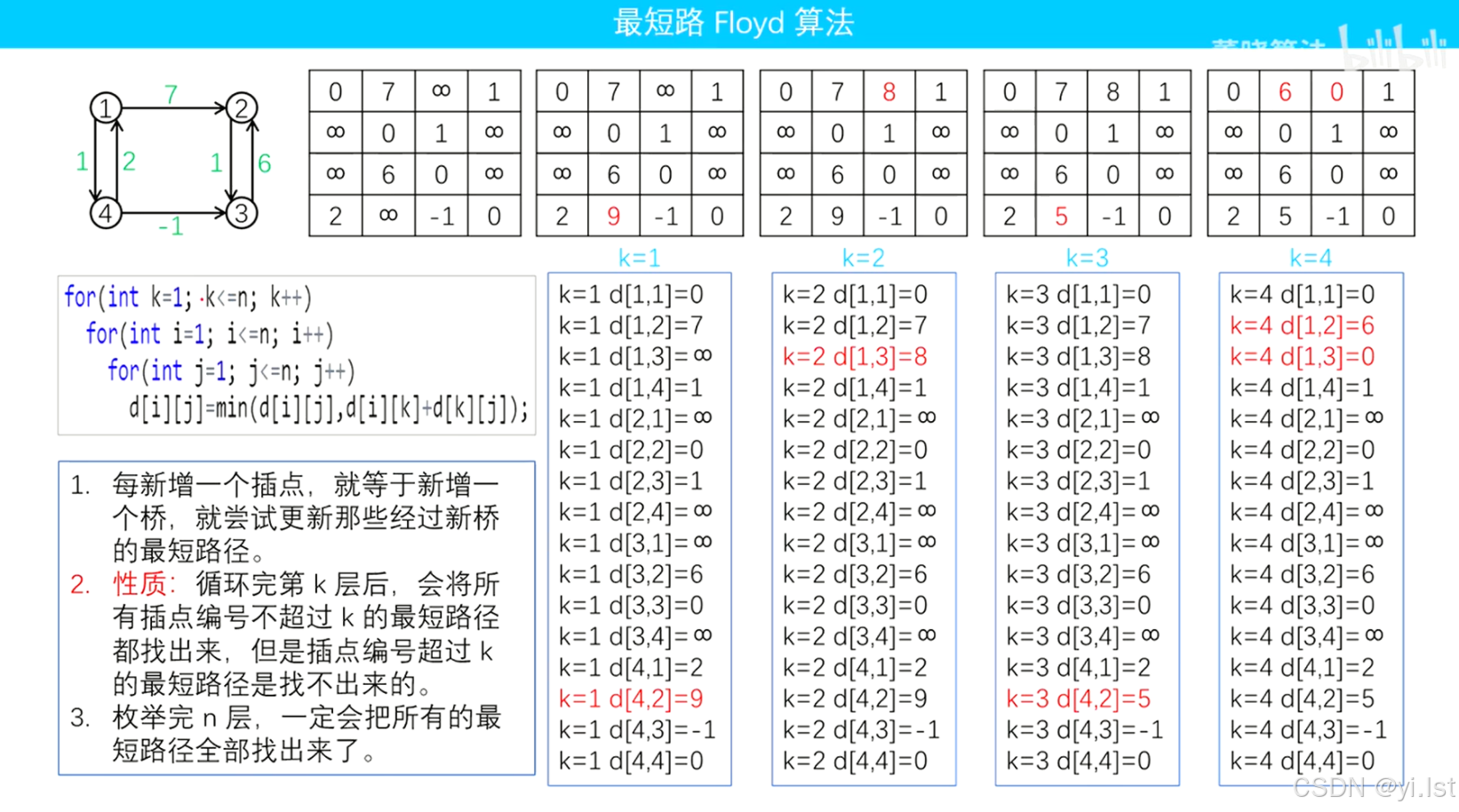
经典题目

B3647 【模板】Floyd - 洛谷

代码

cpp 复制代码

// Problem: 洛谷B3647 【模板】Floyd
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/B3647
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Submission Time: 2025-08-21 17:00:45

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fi first
#define se second 
#define endl '\n'
const int INF = 1e18;
const int N = 1e2+5;
int dp[N][N];
int n,m;
string s;
void solve()
{
	cin >> n >> m;//点的个数和边的个数
	fill(&dp[0][0],&dp[0][0]+N*N,INF);
	for(int i = 0; i <= n; i++) dp[i][i] = 0; //自环为0
	for(int i=1; i<=m; i++)
	{
		int u,v,w;
		cin >> u >> v >> w;
		dp[u][v]=min(dp[u][v],w);//存双向图，且可能有重边
		dp[v][u]=dp[u][v];
	}
	for(int k=1; k<=n; k++)//递推式
		for(int i=1; i<=n; i++)
			for(int j=1; j<=n; j++)
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
				
	for(int i=1; i<=n; i++)
	{
		for(int j=1; j<=n; j++)
			cout << dp[i][j] <<  ' ';
		cout << endl;
	}
}
signed main()
{
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T=1;
	// cin >> T;
	while(T--) solve();
	return 0;
}

97. 小明逛公园

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fi first
#define se second 
#define endl '\n'
const int INF = 1e18;
const int N = 1e2+5;
int dp[N][N];
int n,m;
void solve()
{
	cin >> n >> m;//点的个数和边的个数
	fill(&dp[0][0],&dp[0][0]+N*N,INF);
	for(int i = 0; i <= n; i++) dp[i][i] = 0; //自环为0
	for(int i=1; i<=m; i++)
	{
		int u,v,w;
		cin >> u >> v >> w;
		dp[u][v]=min(dp[u][v],w);//存双向图，且可能有重边
		dp[v][u]=dp[u][v];
	}

	for(int k=1; k<=n; k++)//递推式
		for(int i=1; i<=n; i++)
			for(int j=1; j<=n; j++)
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
	int q;
	cin >> q;
	while(q--)
	{
		int x,y;
		cin >> x >> y;
		if(dp[x][y]==INF) cout << -1 << endl;
		else cout << dp[x][y] << endl;
	}
	// for(int i=1; i<=n; i++)
	// {
		// for(int j=1; j<=n; j++)
			// cout << dp[i][j] <<  ' ';
		// cout << endl;
	// }
}
signed main()
{
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T=1;
	// cin >> T;
	while(T--) solve();
	return 0;
}