
🎁个人主页: 工藤新一¹
🔍系列专栏: C++面向对象(类和对象篇)
🌟心中的天空之城,终会照亮我前方的路
🎉欢迎大家点赞👍评论📝收藏⭐文章
文章目录
二叉树
一、二叉树的概念与结构
-
树是一种递归的结构
-
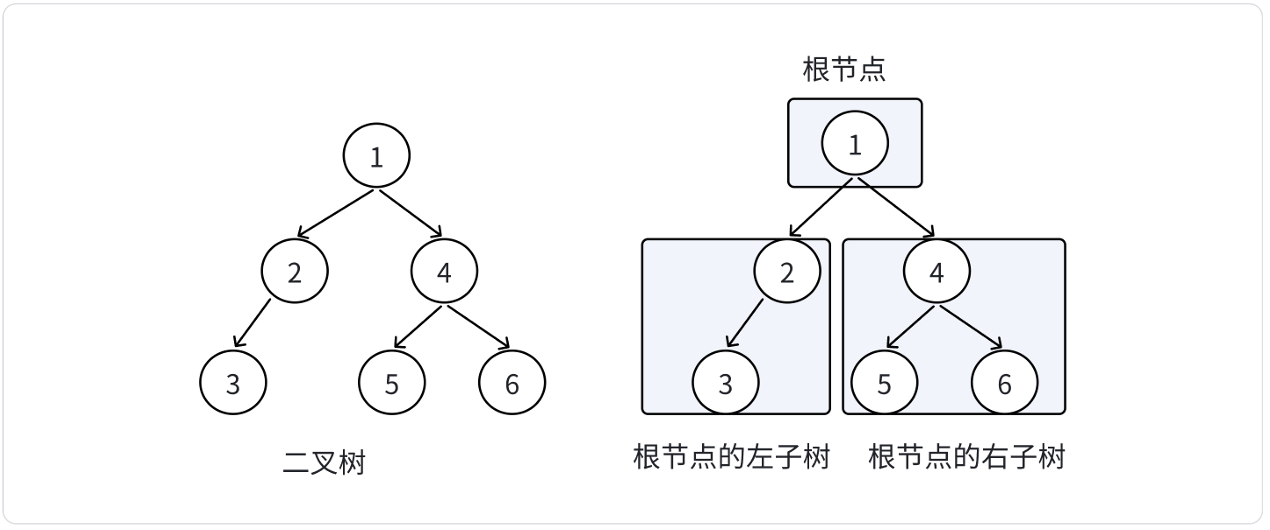
在树形结构中,我们最常用的就是二叉树 。一颗二叉树的节点是一个有限的集合 ,该集合由一个根节点,再加上两颗别称为左子树 和右子树的二叉树组成
二、几种常见的树
2.1二叉树、满二叉树
-
二叉树 不存在 "度" 大于
2的节点 -
二叉树的子树一定有序(有左右之分),次序不能颠倒,因此二叉树是一颗有序树
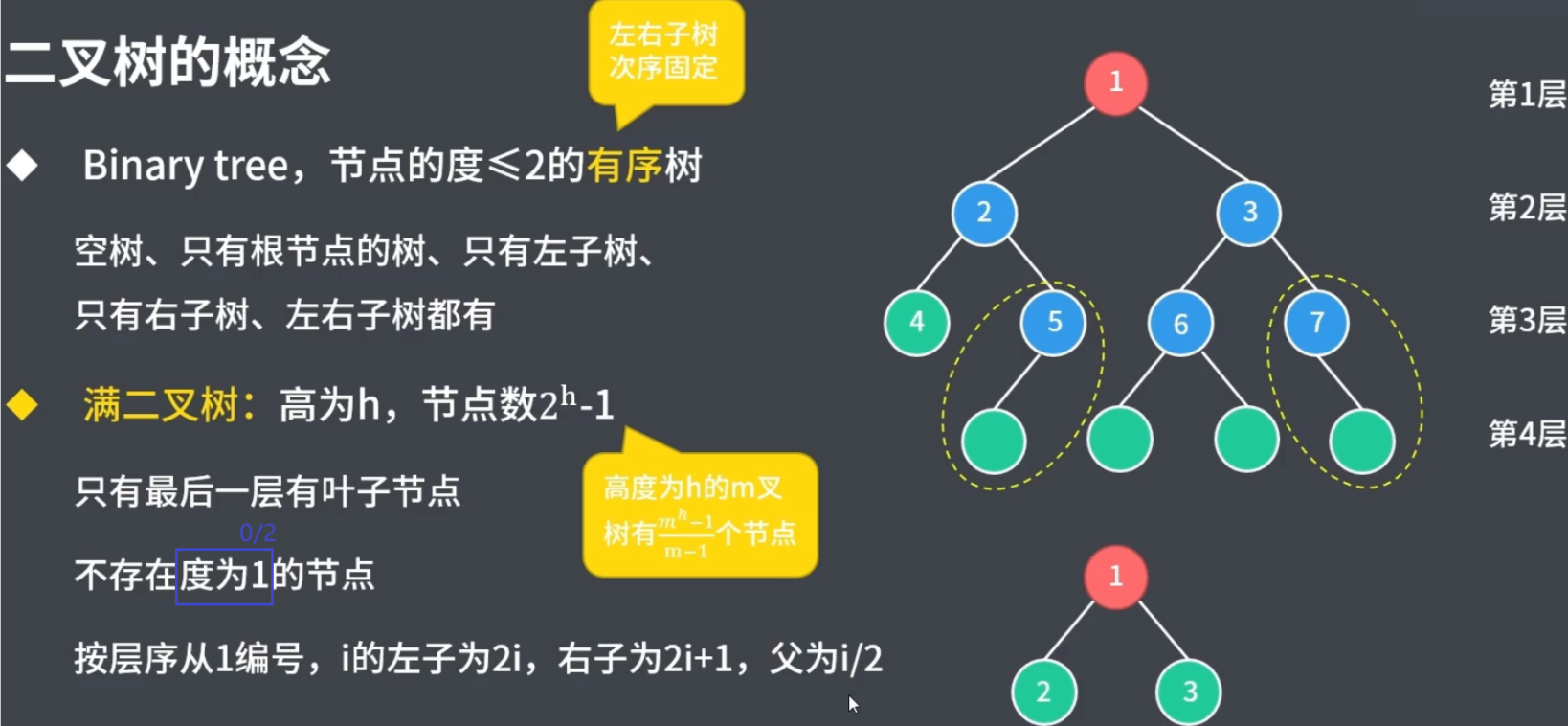
- 满二叉树(理想化的二叉树): 二叉树的每一层的节点达到最大值 ,也就是说,如果一个二叉树的层数 为
K,那么其总节点数是 2k - 1,则其就为满二叉树
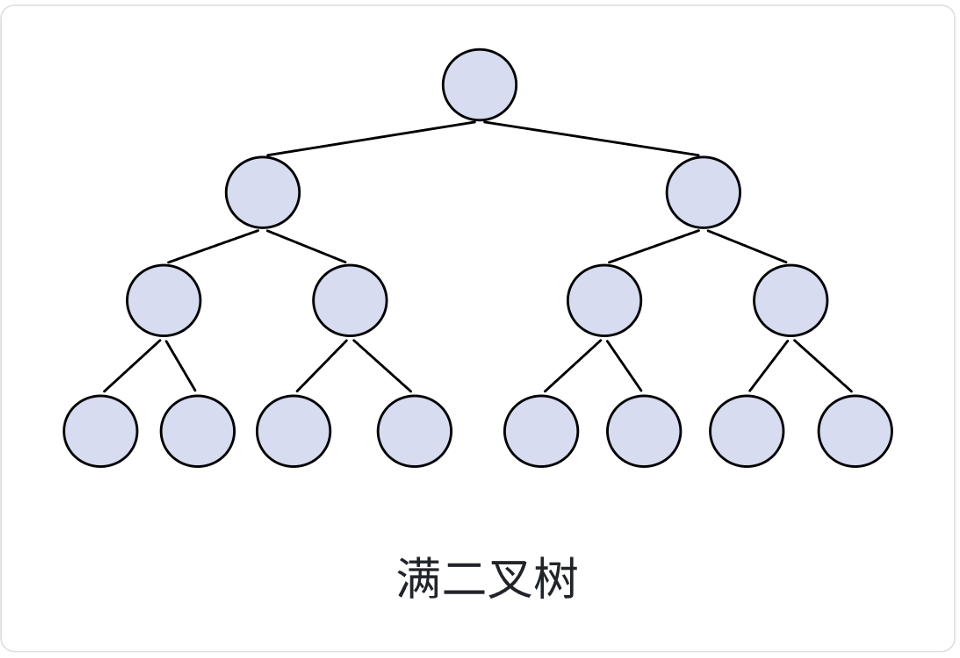
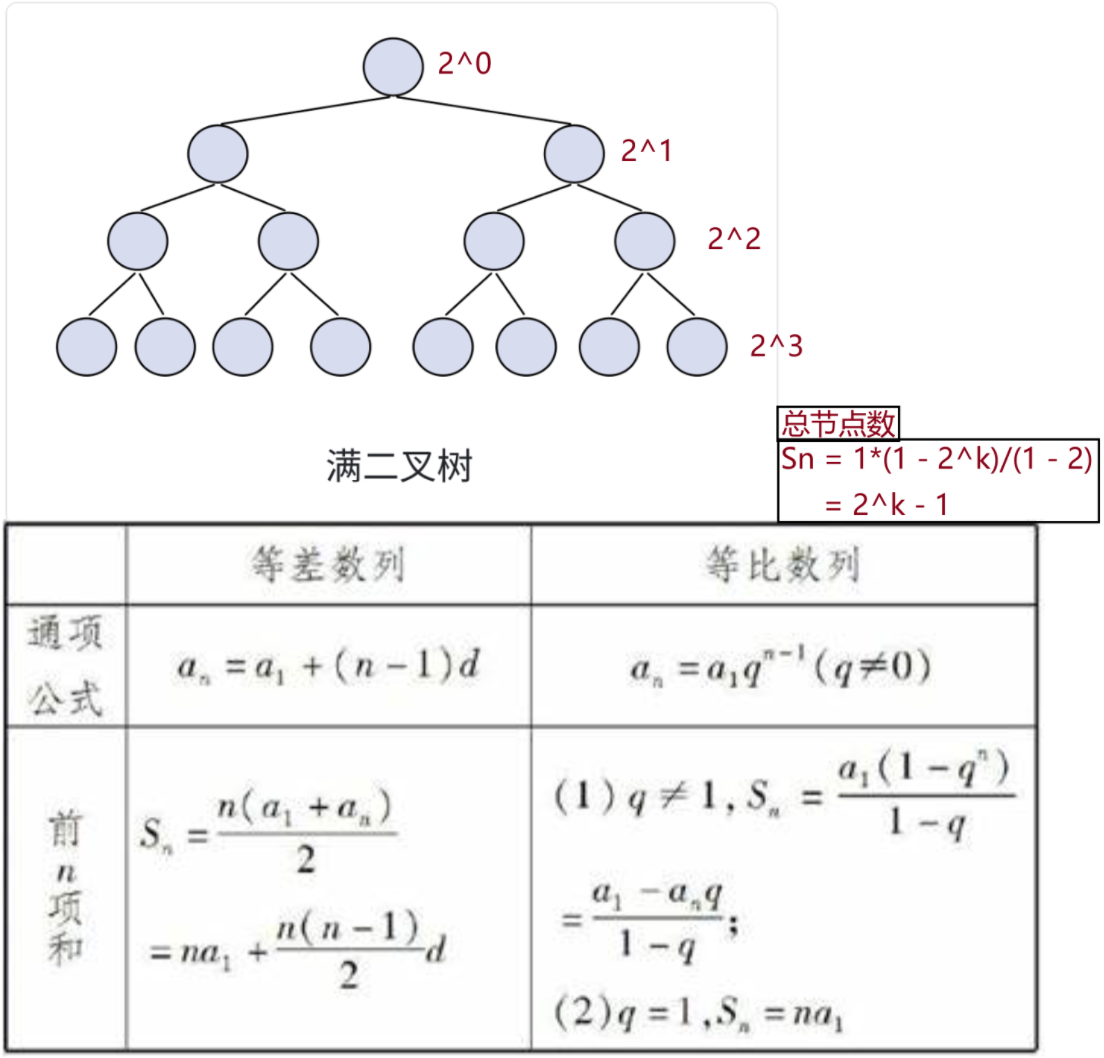
- 满二叉树 :第 K 层节点个数是 2k-1
2.2完全二叉树
- 满二叉树 是完全二叉树 中的子集 (满二叉树是(特殊的)完全二叉树 ),其是一个效率很高的数据结构
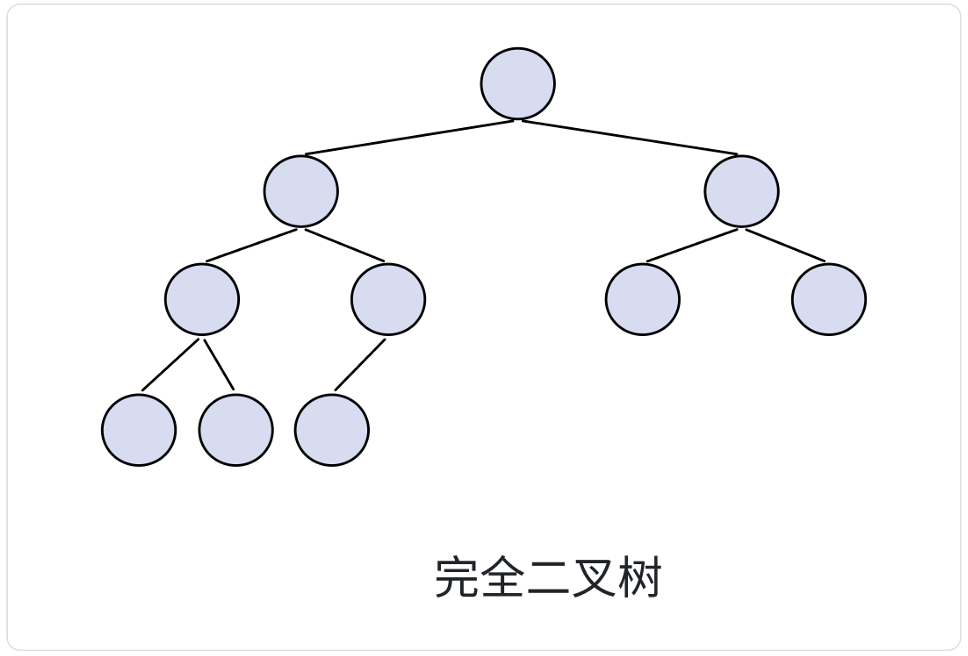
对于深度为 K ,有 n 个节点的二叉树,当且仅当其每一个节点都与深度为 K 的满二叉树中编号从 1 到 n 的节点一 一对应时(节点从左到右依次排列)称之为完全二叉树。
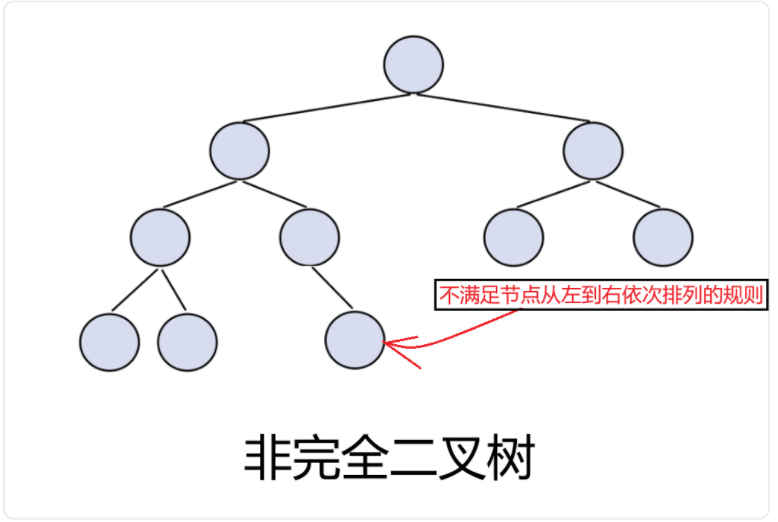
- 最后一层节点个数未达到最大:完全二叉树
- 最后一层节点个数达到最大:即是完全二叉树,又是满二叉树


- 完全二叉树
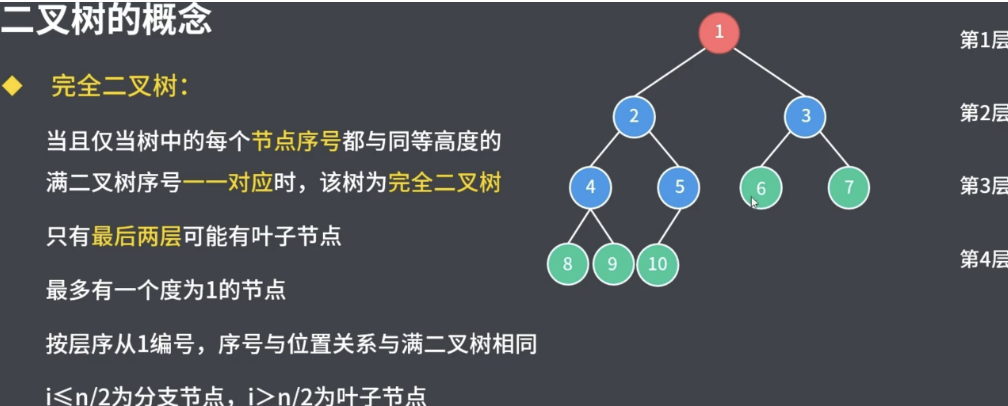
非完全二叉树


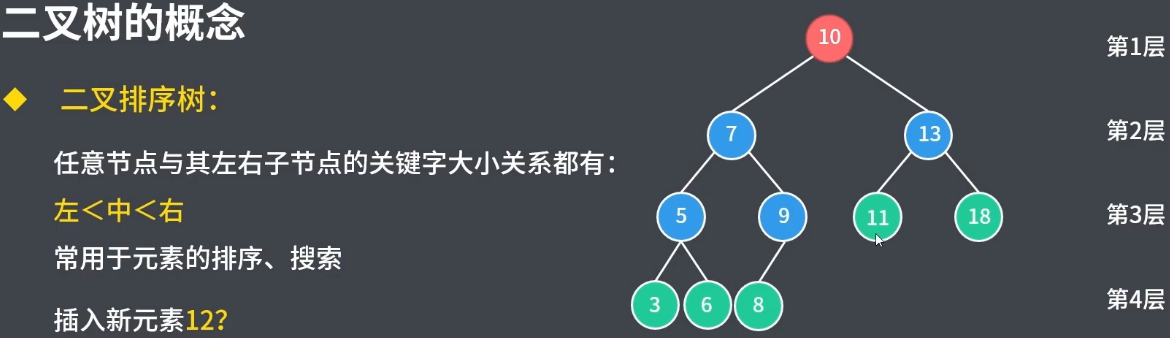
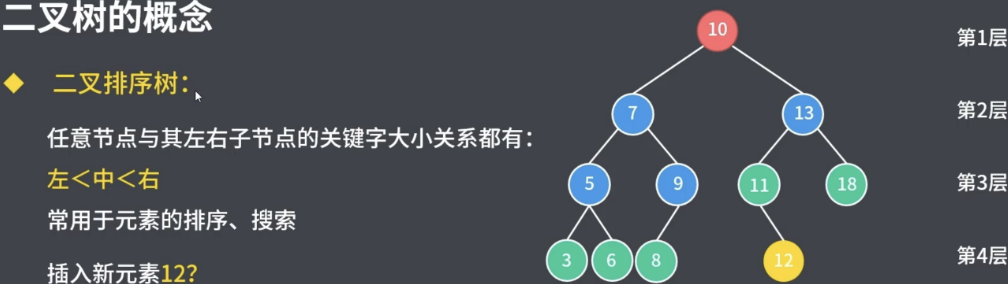
2.3二叉排序树
常用于非重复元素的排序、搜索;对二叉排序树进行左中右遍历可以获取到有序的元素串
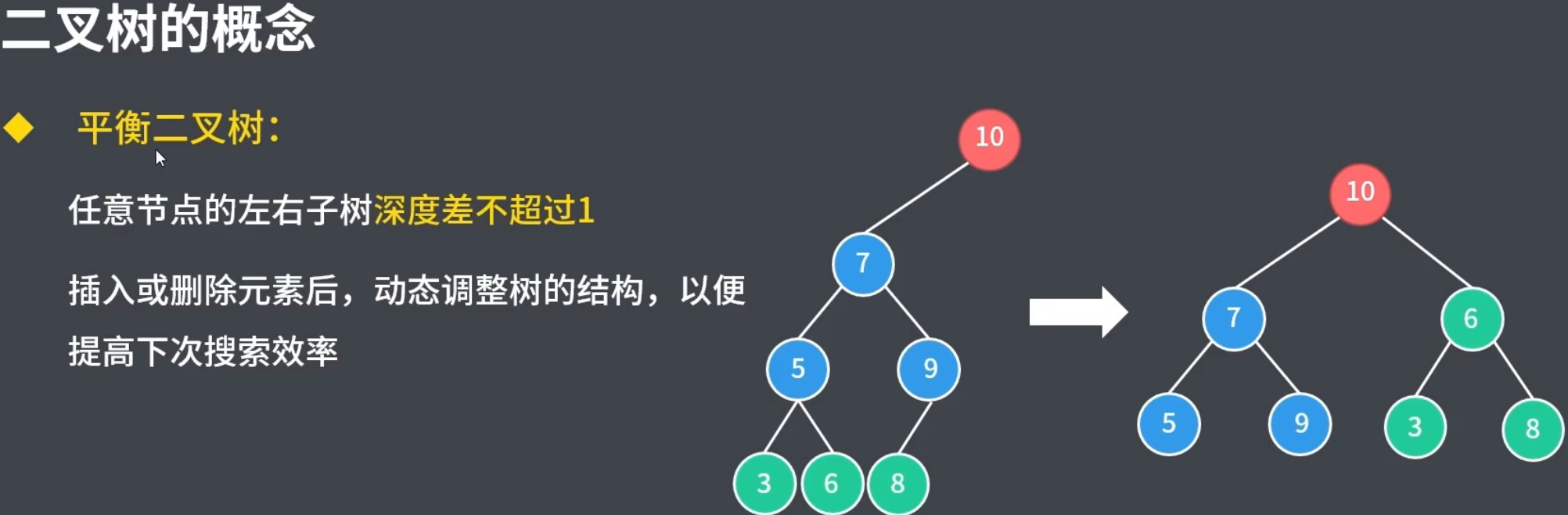
2.4平衡二叉树
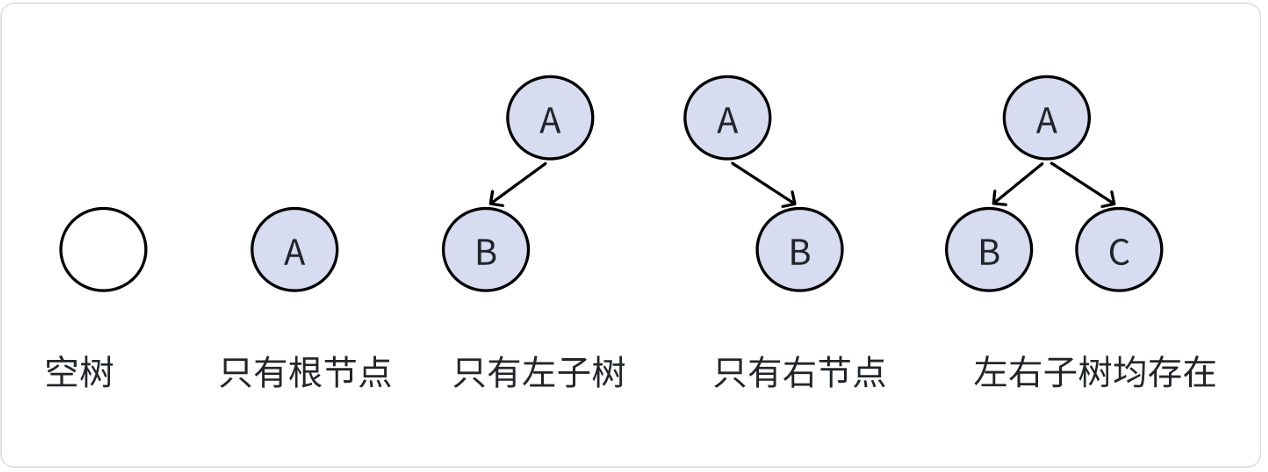
注意:对于任意的二叉树都是由下列几种情况复合而成
三、二叉树的性质
在 二叉树 中,叶子节点个数 == 分支节点个数 + 1
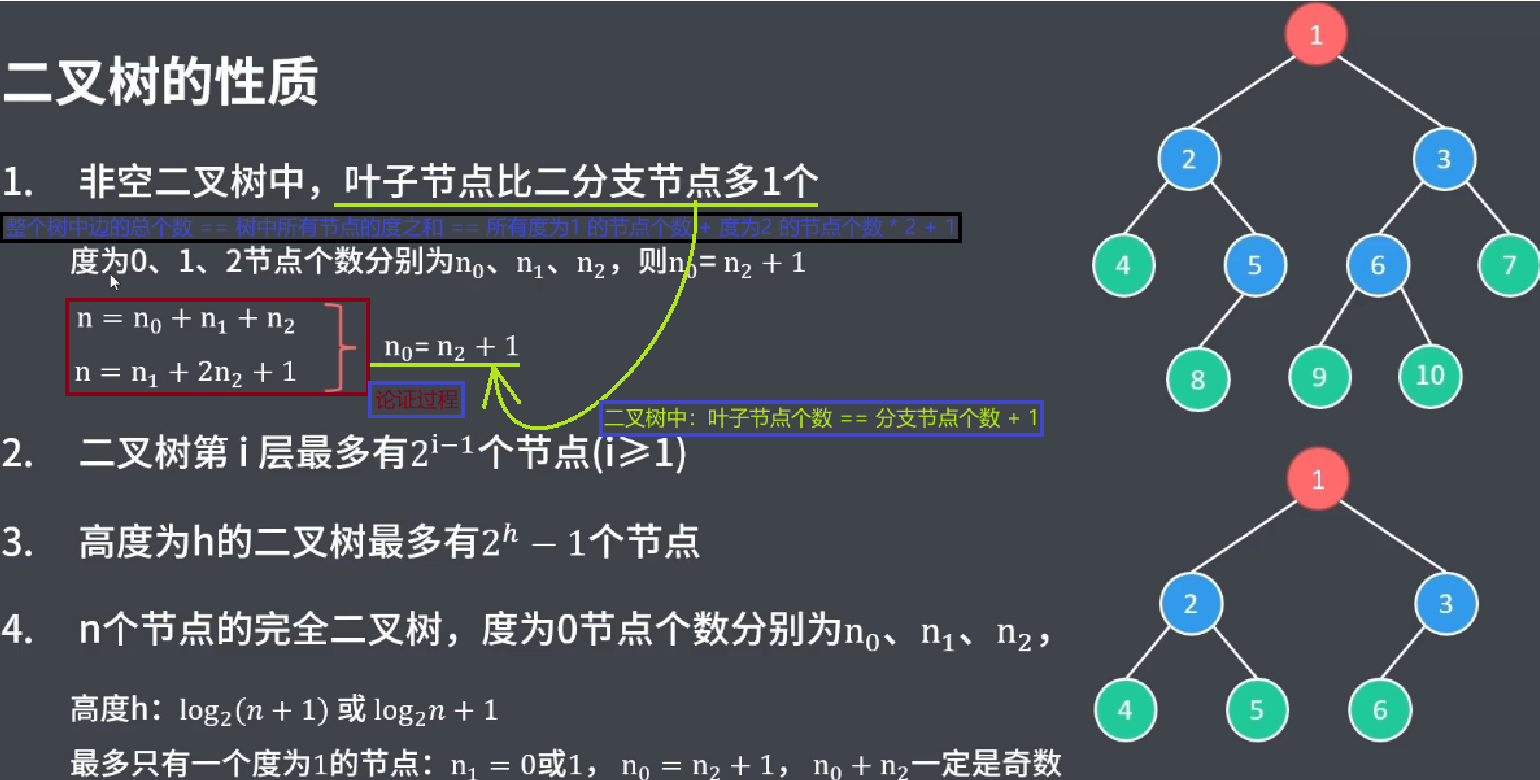
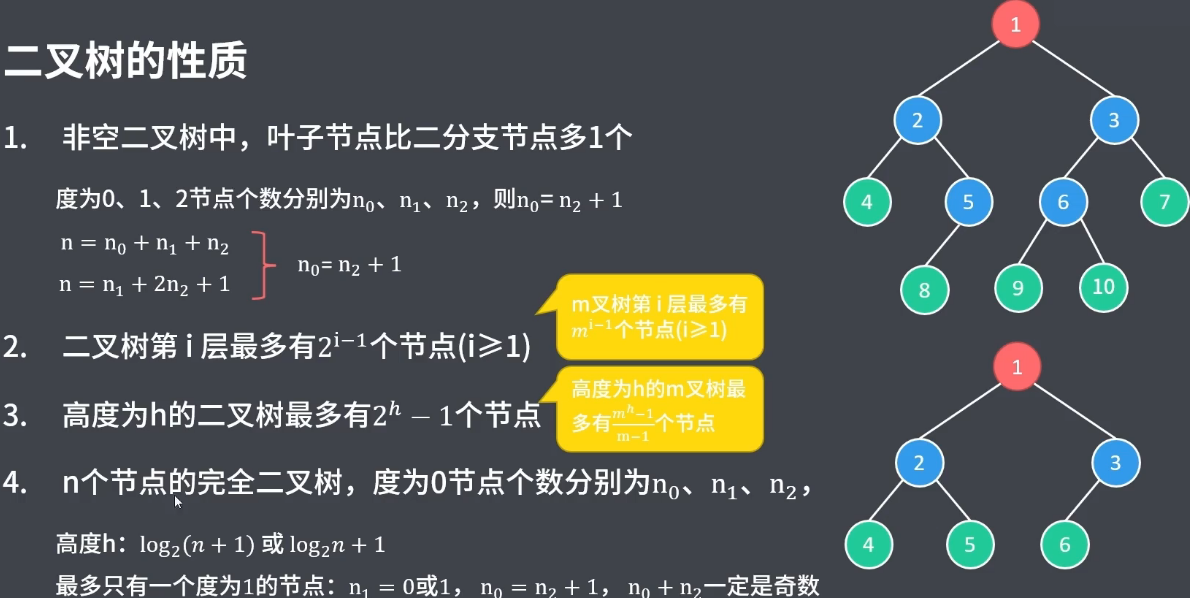
完全二叉树中,最多只有一个度为1的节点: n1 = 0 或 n1 = 1;
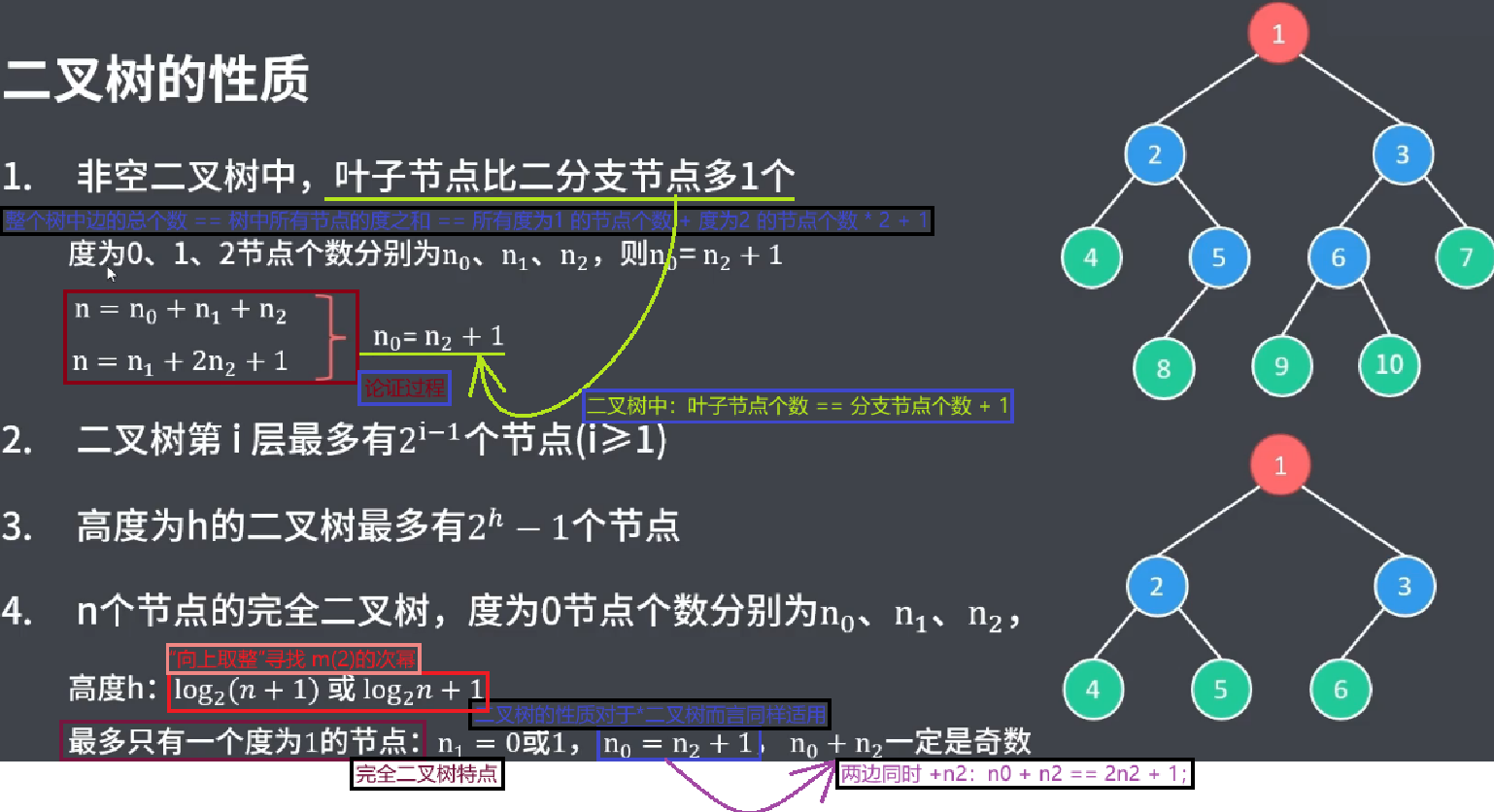
因此,给定节点个数 n,即可求得 n0 n1 n2(因为 完全二叉树特点:n1为定值)
🌟 各位看官好,我是工藤新一¹呀~
🌈 愿各位心中所想,终有所致!