
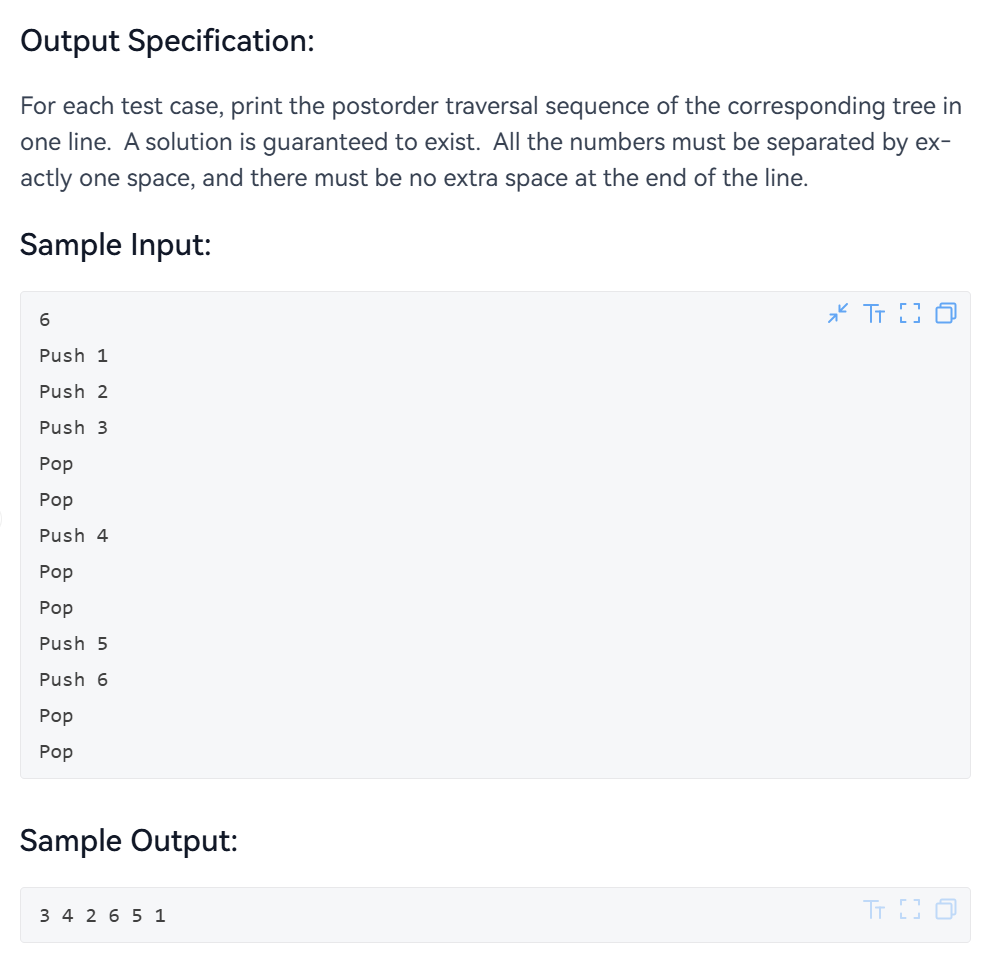
这一题的大意是说给出N个点,然后用栈的方式来建树,通过入栈和出栈的顺序来建立一棵二叉树,建立好树后,输出其后序遍历的序列。
我的思路是,根据题目中的入栈出栈,模拟建树,建好树后输出其后序遍历序列。
我刚开始采用的是用指针来构造树,比较麻烦,容易出错:
cpp
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
#include <limits.h>
#include <queue>
#include <string.h>
#include <stack>
using namespace std;
// 123456789
struct node
{
int data;
struct node* l;
struct node* r;
}tree;
int N;
stack<int> stackk;
node* insert(int id,node* root)
{
if(root==nullptr)
{
root=(node*)malloc(sizeof(node));
root->data=id;
root->l=nullptr;
root->r=nullptr;
return root;
}
else
{
if(root->l!=nullptr)
{
root->l=insert(id,root->l);
}
else
{
root->r=insert(id,root->r);
}
}
}
node* dfsfind(node* root,int topid)
{
if(root==nullptr)
{
return nullptr;
}
if(root->data!=topid)
{
if(root->l!=nullptr)
{
root=dfsfind(root->l,topid);
if(root!=nullptr)
{
return root;
}
}
if(root->r!=nullptr)
{
root=dfsfind(root->r,topid);
if(root!=nullptr)
{
return root;
}
}
}
else
{
return root;
}
}
void postorder(node* root)
{
if(root==nullptr)
{
return ;
}
postorder(root->l);
postorder(root->r);
cout<<root->data<<" ";
}
int main()
{
//ios::sync_with_stdio(0),cin.tie(0),cout.tie(
cin>>N;
node* root=nullptr;
int topid=0;
for(int i=0;i<2*N;i++)
{
string s;
int id;
cin>>s;
if(s=="Push")
{
cin>>id;
stackk.push(id);
if(topid!=0)
{
node* temp=dfsfind(root,topid);
temp=insert(id,temp);
cout<<temp->data<<endl;
topid=0;
}
else
{
root=insert(id,root);
}
}
else
{
topid=stackk.top();
stackk.pop();
}
}
postorder(root);
return 0;
} 这个代码不能通过。
对于PAT这种算法竞赛,在写树或者链表等数据结构的时候尽可能的用数组来模拟。这样的话比较方便,不容易写错,而且数组模拟可以直接获取下标,很方便。
于是:
cpp
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
#include <limits.h>
#include <queue>
#include <string.h>
#include <stack>
using namespace std;
// 123456789
struct node
{
int data;
int l;
int r;
};
int N;
stack<int> st;
int cnt;
void postorder(vector<node> &tree,int root)
{
if(root==-1)
{
return ;
}
postorder(tree,tree[root].l);
postorder(tree,tree[root].r);
if(cnt!=0)
cout<<" ";
cout<<tree[root].data;
cnt++;
}
int main()
{
//ios::sync_with_stdio(0),cin.tie(0),cout.tie(
cin>>N;
vector<node> tree(N+1);
for(int i=0;i<=N;i++)
{
tree[i].l=-1;
tree[i].r=-1;
tree[i].data=-1;
}
int topid=0;
string s;
for(int i=0;i<N*2;i++)
{
string s;
int x;
cin>>s;
if(s=="Push")
{
cin>>x;
st.push(x);
tree[x].data=x;
if(tree[topid].l==-1)
{
tree[topid].l=x;
}
else
{
tree[topid].r=x;
}
topid=x;
}
else
{
topid=st.top();
st.pop();
}
}
postorder(tree,1);
return 0;
} 
但这有一个测试点不过原因是,我们不能错误的把1这个点当作根节点,因为有可能第一次输入可能不是1.
因此:
cpp
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
#include <limits.h>
#include <queue>
#include <string.h>
#include <stack>
using namespace std;
// 123456789
struct node
{
int data;
int l;
int r;
};
int N;
stack<int> st;
int cnt;
void postorder(vector<node> &tree,int root)
{
if(root==-1)
{
return ;
}
postorder(tree,tree[root].l);
postorder(tree,tree[root].r);
if(cnt!=0)
cout<<" ";
cout<<tree[root].data;
cnt++;
}
int main()
{
//ios::sync_with_stdio(0),cin.tie(0),cout.tie(
cin>>N;
vector<node> tree(N+1);
for(int i=0;i<=N;i++)
{
tree[i].l=-1;
tree[i].r=-1;
tree[i].data=-1;
}
int topid=0;
string s;
bool hasroot=false;
int root;
for(int i=0;i<N*2;i++)
{
string s;
int x;
cin>>s;
if(s=="Push")
{
cin>>x;
//cout<<x<<endl;
if(hasroot==false)
{
hasroot=true;
root=x;
}
st.push(x);
tree[x].data=x;
//cout<<tree[x].data<<endl;
if(tree[topid].l==-1)
{
tree[topid].l=x;
}
else
{
tree[topid].r=x;
}
topid=x;
}
else
{
topid=st.top();
st.pop();
}
}
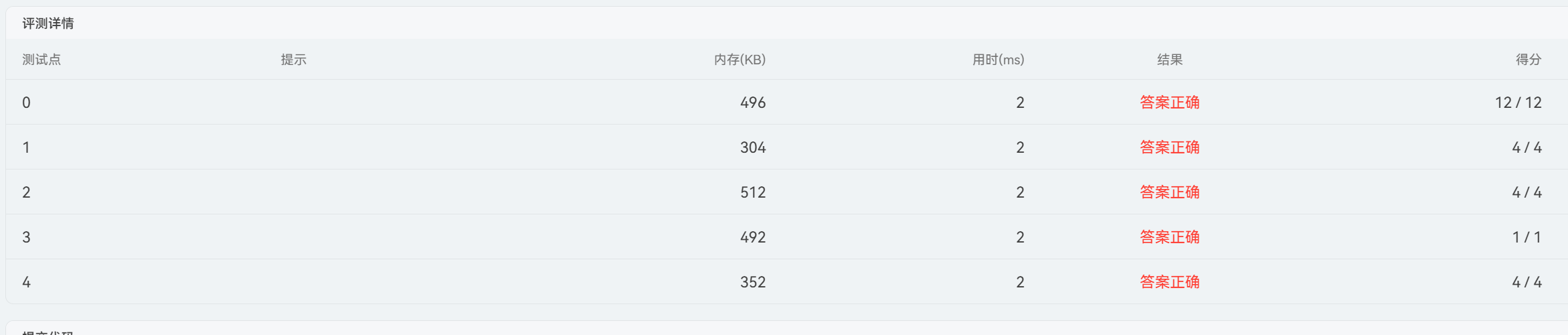
postorder(tree,root);
return 0;
} 成功通过
我在网上看到这一题还可以不建树来写
因为入栈顺序push恰好是前序遍历左右根,出栈顺序pop恰好是中序序列左根右,根据前序序列和中序序列是得到后序序列的:
原理
前序序列的第一个元素 = 根节点。
在中序序列中找到该根的位置:
左边部分 → 左子树的中序
右边部分 → 右子树的中序
在前序序列中,根之后的一段对应左子树,另一段对应右子树。
这样就能递归恢复二叉树。
得到树以后,再做一次后序遍历即可。
这里不详细叙述了。
有一道类似的题目:
已知后序遍历和中序遍历,求层次遍历: