Leetcode 深度优先搜索 (15)

二叉树最大路径和 (LeetCode 124)

题目

给定二叉树根节点 root。路径：相邻节点之间均有边，同一节点在一条路径中至多出现一次；可不经过根；至少包含一个节点。路径和为节点值之和。求最大路径和。

示例 1：

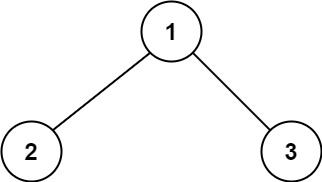
输入：root = [1,2,3]

输出：6

解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

---

解题思路总览

1. 后序 DFS + 全局变量（核心模板 / 推荐）
2. 分治返回结构体 Info（多字段易扩展）
3. 迭代后序（栈模拟递归，避免深递归栈风险）
4. 扩展：同时恢复最大路径（在递归中记录选择）
5. 暴力 / 枚举节点作为拐点的低效写法（理解对比，不推荐）

---

思路一：后序 DFS（推荐）

原理与适用场景

单次后序遍历。对每个节点，只需：

1. 取左右子树"向下单腿增益"(若为负置 0 不取，代表放弃该方向)；
2. 用 node.val + leftGain + rightGain 更新全局最大（该值表示路径在此节点拐弯、可含两条腿）；
3. 向父节点返回"只能带一条腿"的最大值 node.val + max(leftGain, rightGain)，避免路径在更高层重复分叉。
   适用于：仅需最大和，不需重建路径；数据量 n ≤ 2e5（递归深度若树退化且语言栈限制需谨慎）。

实现步骤

1. 设全局变量 ans = -∞。
2. 递归函数 dfs：空节点返回 0。
3. 计算左右增益：l = max(0, dfs(left))，r = max(0, dfs(right))。
4. 更新答案：ans = max(ans, node.val + l + r)。
5. 返回：node.val + max(l, r)。
6. 主函数返回 ans。

JAVA 代码实现

class Solution {
	static class TreeNode { int val; TreeNode left, right; TreeNode(int v){ val=v; } }
	private int ans = Integer.MIN_VALUE;
	public int maxPathSum(TreeNode root) {
		dfs(root);
		return ans;
	}
	private int dfs(TreeNode node){
		if(node == null) return 0;
		int left = Math.max(0, dfs(node.left));
		int right = Math.max(0, dfs(node.right));
		ans = Math.max(ans, node.val + left + right); // 拐点候选
		return node.val + Math.max(left, right);       // 单腿返回
	}
}

---

思路二：分治返回结构体 Info

原理与适用场景

封装三个量：

• bestDown：从此节点向下单腿最大增益
• bestThrough：以此节点为拐点（左右可各取一次）最大值
• bestAll：该子树内部全局最大路径和
  自底向上合并，最终答案为根的 bestAll。适合需要额外扩展（如调试、再增加字段）场景。

实现步骤

1. 空节点：bestDown = 0；bestThrough = bestAll = -∞（避免被误取）。
2. 合并：
   • 取左右 Info：L, R。
   • bestDown = node.val + max(0, max(L.bestDown, R.bestDown))
   • bestThrough = node.val + Math.max(0,L.bestDown) + Math.max(0,R.bestDown)
   • bestAll = max( max(L.bestAll, R.bestAll), bestThrough )
3. 返回新 Info。

JAVA 代码实现

class Solution {
	static class TreeNode { int val; TreeNode left, right; TreeNode(int v){ val=v; } }
	static class Info { int bestDown, bestThrough, bestAll; Info(int d,int t,int a){bestDown=d;bestThrough=t;bestAll=a;} }
	public int maxPathSum(TreeNode root){ return solve(root).bestAll; }
	private Info solve(TreeNode n){
		if(n==null) return new Info(0, Integer.MIN_VALUE, Integer.MIN_VALUE);
		Info L = solve(n.left), R = solve(n.right);
		int bestDown = n.val + Math.max(0, Math.max(L.bestDown, R.bestDown));
		int bestThrough = n.val + Math.max(0,L.bestDown) + Math.max(0,R.bestDown);
		int bestAll = Math.max(Math.max(L.bestAll, R.bestAll), bestThrough);
		return new Info(bestDown, bestThrough, bestAll);
	}
}

---

思路三：迭代后序（栈模拟）

原理与适用场景

用显式栈模拟后序，避免极端深度导致的递归栈溢出。对节点的计算仍与思路一一致，只是手动管理访问顺序和缓存其左右增益。

适合：语言栈深度有限或输入可能退化为链；不方便修改 JVM 栈参数。

实现步骤

1. 两个栈或一个栈 + 标记：典型后序模板（先根入栈，遍历时把左右入栈，生成"逆后序"列表再逆序处理）。
2. 使用 Map<TreeNode,Integer> 存储单腿增益。
3. 第二阶段按后序顺序计算：取左右增益（若不存在视为 0）；更新全局答案；写回该节点单腿。
4. 根节点单腿不直接用，最终输出全局答案。

JAVA 代码实现

import java.util.*;
class Solution {
	static class TreeNode { int val; TreeNode left, right; TreeNode(int v){ val=v; } }
	public int maxPathSum(TreeNode root) {
		if(root == null) return 0; // 题意通常 root 不为空
		List<TreeNode> post = new ArrayList<>();
		Deque<TreeNode> stack = new ArrayDeque<>();
		stack.push(root);
		while(!stack.isEmpty()){ // 生成根->右->左序列
			TreeNode cur = stack.pop();
			post.add(cur);
			if(cur.left!=null) stack.push(cur.left);
			if(cur.right!=null) stack.push(cur.right);
		}
		int ans = Integer.MIN_VALUE;
		Map<TreeNode,Integer> down = new IdentityHashMap<>();
		// 逆序即后序：左 右 根
		for(int i=post.size()-1;i>=0;i--){
			TreeNode n = post.get(i);
			int l = n.left==null?0:Math.max(0, down.get(n.left));
			int r = n.right==null?0:Math.max(0, down.get(n.right));
			ans = Math.max(ans, n.val + l + r);
			down.put(n, n.val + Math.max(l, r));
		}
		return ans;
	}
}

---

思路四：返回最大和同时恢复路径

原理与适用场景

在思路一的基础上，想得到具体节点序列。关键：记录在更新全局答案时，当前节点及其左右被采纳的"正增益链"。可在 DFS 时返回单腿最大链（列表），并在更新全局时构造新答案路径。适用于需要输出具体路径用于调试或题目扩展。

实现步骤

1. DFS 返回：节点向上的单腿最大链（List，头为当前节点）。
2. 计算左右链及其和；若和为负则丢弃该边。
3. 更新全局：node + leftChain(若用) + rightChain(若用) 拼成完整路径（需注意左右方向）。
4. 向父节点返回：node + (较大单腿链)。

JAVA 代码实现（仅示意，核心逻辑）

import java.util.*;
class SolutionWithPath {
	static class TreeNode { int val; TreeNode left, right; TreeNode(int v){ val=v; } }
	private int best = Integer.MIN_VALUE;
	private List<TreeNode> bestPath = new ArrayList<>();
	public int maxPathSum(TreeNode root){
		dfs(root);
		// 若需要输出路径，可遍历 bestPath
		return best;
	}
	private List<TreeNode> dfs(TreeNode n){
		if(n==null) return Collections.emptyList();
		List<TreeNode> left = dfs(n.left);
		List<TreeNode> right = dfs(n.right);
		int leftSum = sum(left), rightSum = sum(right);
		int takeLeft = Math.max(0, leftSum);
		int takeRight = Math.max(0, rightSum);
		int through = n.val + takeLeft + takeRight;
		if(through > best){
			best = through;
			List<TreeNode> path = new ArrayList<>();
			if(takeLeft>0){ List<TreeNode> revL = new ArrayList<>(left); Collections.reverse(revL); path.addAll(revL); }
			path.add(n);
			if(takeRight>0){ path.addAll(right); }
			bestPath = path;
		}
		if(takeLeft==0 && takeRight==0){
			return new ArrayList<>(Collections.singletonList(n));
		} else if(leftSum >= rightSum){
			List<TreeNode> ret = new ArrayList<>(left);
			ret.add(0, n);
			return ret;
		} else {
			List<TreeNode> ret = new ArrayList<>(right);
			ret.add(0, n);
			return ret;
		}
	}
	private int sum(List<TreeNode> chain){ int s=0; for(TreeNode t:chain) s+=t.val; return s; }
}

说明：为直观演示，未对性能（重复求和）做极致优化，可在返回结构中同时携带链和和。

---

思路五：暴力枚举拐点（不推荐）

原理与适用场景

对每个节点作为拐点，单独计算最大左下腿 + 右下腿 + 自身。若每次重新 DFS 计算下行最大，会导致 O(n^2)。用于理解最优解"为何必须共享子问题结果"。

实现步骤（概念）

1. 枚举节点 x。
2. 计算从 x 左子树出发的最大下行路径（独立 DFS）。
3. 同理右子树。
4. 统计答案。

JAVA 代码实现（示意/低效）

class SlowSolution {
	static class TreeNode { int val; TreeNode left,right; TreeNode(int v){val=v;} }
	public int maxPathSum(TreeNode root){
		if(root==null) return 0;
		int ans = Integer.MIN_VALUE;
		java.util.List<TreeNode> list = new java.util.ArrayList<>();
		collect(root, list);
		for(TreeNode n: list){
			int l = Math.max(0, maxDown(n.left));
			int r = Math.max(0, maxDown(n.right));
			ans = Math.max(ans, n.val + l + r);
		}
		return ans;
	}
	private void collect(TreeNode n, java.util.List<TreeNode> list){ if(n==null) return; list.add(n); collect(n.left,list); collect(n.right,list); }
	private int maxDown(TreeNode n){
		if(n==null) return 0;
		return n.val + Math.max(0, Math.max(maxDown(n.left), maxDown(n.right))); // 重复计算
	}
}

---

补充说明（比较与复杂度）

思路	时间复杂度	空间复杂度	额外结构	优点	缺点	适用
1 后序 DFS	O(n)	O(h) 递归栈	常数	代码短，性能最优	需递归	一般场景
2 分治 Info	O(n)	O(h)	小对象	字段清晰，易扩展	稍冗长	需扩展信息
3 迭代后序	O(n)	O(h) 栈	Map/栈	无递归风险	代码更长	深链 / 栈敏感
4 带路径	O(n)	O(h)	维护链	可得具体路径	处理链操作稍复杂	需要路径
5 暴力	O(n^2) 最坏	O(h)	无	易理解原理	超时	仅教学

说明：h 为树高（平衡时 ~log n，退化链时 n）。若节点值全为负，算法 1/2/3 均会正确返回最大单节点值，因为左右增益为 0，不会把负腿继续加上。

关键正确性总结

1. "单腿返回 + 两腿只在节点内部聚合" 确保路径不会重复分叉。
2. 截断负增益保证不会让路径和减少，相当于取 max(0, downGain)。
3. 全局答案更新独立于返回值，因此可以不经过根。
4. 所有方法都只在节点常数时间处理（除暴力）。

---

一眼记忆模板（核心）

int dfs(TreeNode n){
	if(n==null) return 0;
	int l = Math.max(0, dfs(n.left));
	int r = Math.max(0, dfs(n.right));
	ans = Math.max(ans, n.val + l + r);
	return n.val + Math.max(l, r);
}

---

结论

使用后序 DFS 模板即可高效解决；理解"单腿返回 + 拐点更新"是该题核心。其思想可迁移到：二叉树最大直径（把权值改成边权并计长度）、最大路径乘积（需处理负数双最值）等扩展问题。