206. 反转链表
一、题目
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
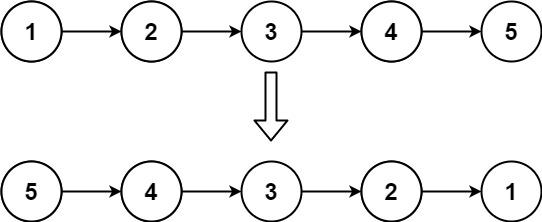
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
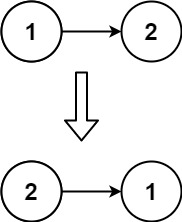
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目范围是 [0, 5000]
- -5000 <= Node.val <= 5000
进阶:链表可以选用迭代 或递归方式完成反转。你能否用两种方法解决这道题?
二、思路
根据题目的进阶要求,我们接下来使用递归法和迭代法两种方法来解决这个算法题目。
递归法:
自己调用自己。识别方法:在reverse函数的代码身体里,又看到了reverse(...)这个名字。
- 判断终止条件
- 使用temp暂存下一步
- 执行反转
- 指针双双后移
迭代法:
使用循环,可以看到 for 或 while 循环。
- 初始化两个 cur 和 pre 指针
- 开启循环,只要cur还有值,就要一直循环
- 使用temp暂存下一步
- 执行反转
- 指针双双后移
- 循环结束时,返回pre,结束
三、代码
递归法:
javascript
//递归辅助函数
function reverse(cur,pre){
// 1. 终止条件 (Base Case)
// 如果 cur 为空,说明已经越过了链表的最后一个节点。
// 此时 pre 指向的就是原链表的最后一个节点(也就是新链表的头节点)。
// 将其返回,这个返回值会像接力棒一样一层层传回主函数,return后终止了。
if(!cur) return pre;
// 2. 暂存下一步 (Save Next)
// 因为接下来要切断 cur 和后面的联系,所以必须先把 cur.next 存起来,
// 否则后面的一长串链表就丢了。
const temp = cur.next;
//3. 执行反转
cur.next = pre;
//进入下一层调用,指针向后移动
//cur后移一位到temp
//pre后移一位到cur
return reverse(temp,cur)
}
//主函数
var reverseList = function(head) {
//当前cur节点是head
//当前pre节点是null
return reverse(head,null);
};迭代法:
javascript
var reverseList = function(head){
//初始化两个指针:pre前驱,cur当前
let pre = null;
let cur = head;
//开启循环,只要cur还有值,就继续干活
while(cur){
//暂存下一步temp(防止断链)
const temp = cur.next;
//反转指针
cur.next=pre;
//将指针集体向后移动,准备处理下一个
pre=cur;//pre移动到当前cur
cur=temp;//当前cur移动到temp(下一位)
}
//循环结束时,cur变成了null,pre刚好停在新的头节点上
return pre;
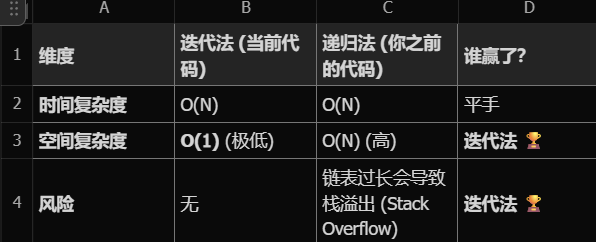
}四、复杂度
递归法:
缺点:这种写法属于尾递归,如果链表特别长,可能会导致栈溢出错误。
时间复杂度:O(N)
- 分析: N 是链表的长度。代码中的递归函数 reverse 会被调用 N+1N+1N+1 次(每个节点一次,最后 null 一次)。
- 操作: 每次调用内部只做了常数次操作(赋值、指针修改),即 O(1)。
空间复杂度:O(N) ⚠️ (这是与迭代法最大的不同)
- 分析: 递归的本质是函数调用栈 (Call Stack)。
- 堆叠:
- 当处理节点 1 时,函数没结束,等着节点 2 的结果;
- 当处理节点 2 时,等着节点 3 的结果...
- 这意味着系统内存中同时保留了 NNN 层函数的上下文(每一层都要存 cur, pre, temp 这些变量)。
迭代法:
时间复杂度:O(N)
结论:线性时间复杂度。
其中 N 是链表的长度(节点数量)。
为什么是 O(N)?
- 一次遍历: 代码中有一个 while (cur) 循环。这个循环从链表的头节点 (head) 开始,顺着 next 指针一直走到尾部 (null)。
- 不走回头路: 每个节点被访问且仅被访问一次。
- 常数级操作: 在循环内部,不管是 temp = cur.next 还是指针的赋值操作,都是最基本的指令,耗时是固定的 O(1)O(1)O(1)。
空间复杂度:O(1)
结论:常数空间复杂度。
这是迭代法相对于递归法最大的优势。
为什么是 O(1)?
- 变量数量固定: 无论链表有 10 个节点还是 10 万个节点,这段代码运行所需的额外内存空间是固定不变的。
- 仅使用的变量: 我们只申请了 3 个指针变量的内存空间:
- pre (前驱)
- cur (当前)
- temp (临时存储)
- 原地操作 (In-Place): 我们直接修改了原链表节点的 next 指针,没有创建新的链表,也没有像递归那样消耗调用栈(Call Stack)空间。
两种方法对比: