算法杂谈：回溯路线

前言

在动态规划中：

在bfs中：

前言

对于普通的路线问题，我们可以存储全局变量path存储路线过程中的，一个个"点"。由于这些点就是按照顺序存储的，路线就是可以直接得到的。

但是如果是动态规划，或者是带有图需要从一个点开始找到另一个点，我们在找到结果后还需要回溯这个结果的实现路线，这里没办法轻松得到路线，那么我们就需要尽可能利用条件，从该结果往回退找到上一个节点是什么，这里介绍两种目前已经遇到的情景。

在动态规划中：

以牛客网最长公共子序列II 为例

最长公共子序列(二)_牛客题霸_牛客网

找到最长子序列，我们还需要返回这个子序列是什么，既然我们已经完成填表，那么我们就可以，以dp值为引，按照dp值递减的顺序，修改i和j的坐标，当s1 $i$ ==s2 $j$ 时此时这个就是我们要寻找的节点，头插进结果，让i--，j--（意味着继续道s1 $0,i-1$ ,s2 $0,j-2$ 区间内寻找）；如果不等，往可以使dp值减少的方向前进，于是我们就找到了路线。

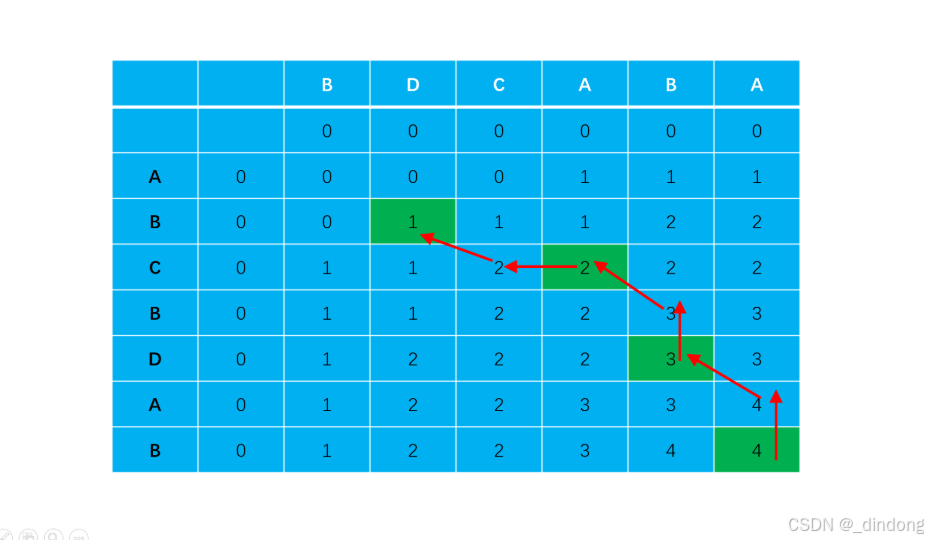
代码实现如下：

cpp 复制代码

class Solution {
public:
    string LCS(string s1, string s2) {
        int n=s1.length(),m=s2.size();
        s1=' '+s1,s2=' '+s2;

        vector<vector<int>> dp(n+1,vector<int>(m+1));
        for(int i=1;i<=n;++i)
        {
            for(int j=1;j<=m;++j)
            {
                if(s1[i]==s2[j])dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        
        //回溯构造LCS
        string ret;
        int i=n,j=m;
        while(i&&j)
        {
            if(s1[i]==s2[j])
            {
                ret=s1[i]+ret;
                --i;
                --j;
            }
            else if(dp[i-1][j]>dp[i][j-1])--i;
            else --j;
        }

        return ret==""?"-1":ret;
    }
};

在bfs中：

以bjfuoj的码码，我迷路了为例

BJFUOJ | 码码，我迷路了

该题是一道很简单的bfs经典题，但找到目标点后，我们还需要输出从起点到目标点依次经过的路径，此时依旧利用回溯，构造路线。

回溯路线：因为我们需要从一个节点得到上一个节点的信息，这里节点的信息就是对应的坐标，那么我们可以创建一个"point"类型的二维数组fa,用fa $i$ $j$ 存储到达点{i,j}的上一个节点的坐标，具体代码体现就是在bfs中队列push新节点的时候，我们得到的节点假设是{newx,newy}，因为newx和newy是由{x,y}得到的，我们使fa $newx$ $newy$ ={x,y}这样就得到了上一个节点的位置，就可以实现回溯了。

此篇完。