Bias / variance and neural networks｜偏差/方差和神经网络

这是我在我的网站中截取的文章，有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn，这里还有很多有关计算机的知识，欢迎进行留言或者来我的网站进行留言！！！

一、偏差与方差权衡

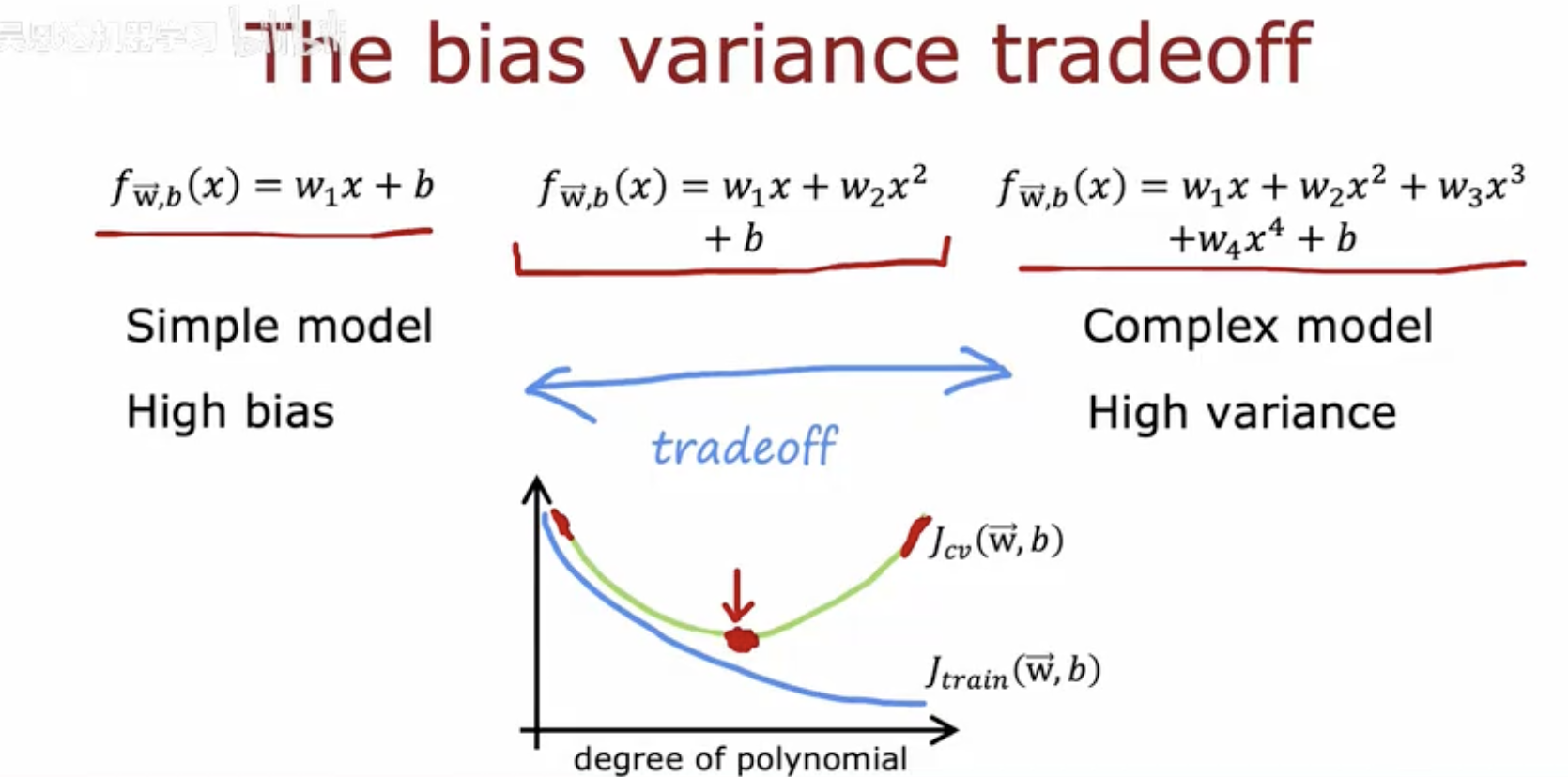
这幅图解释了偏差-方差权衡（bias-variance tradeoff）的概念。图中展示了三个不同复杂度的模型：

简单模型（Simple model）：具有高偏差（High bias），表示模型过于简单，无法捕捉数据的真实模式。
复杂模型（Complex model）：具有高方差（High variance），表示模型过于复杂，容易过拟合训练数据。
图中还展示了一个折中点（tradeoff），即模型复杂度适中时，训练误差（J train(w ,b )）和交叉验证误差（J cv(w ,b)）之间的差异最小，这是理想的模型复杂度。

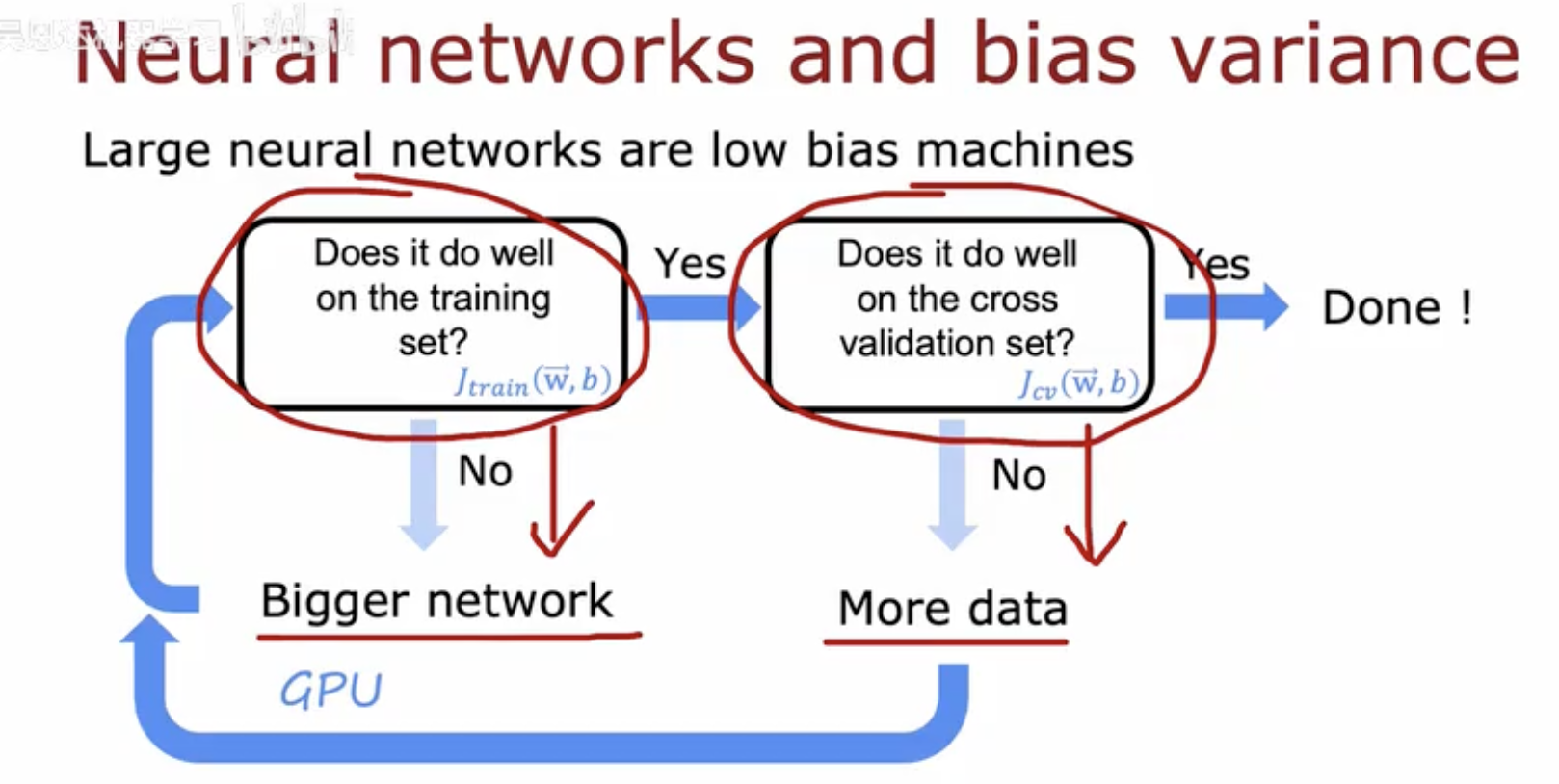
这幅图展示了在训练大型神经网络时如何处理偏差和方差的问题，以及如何通过调整网络大小和数据量来优化模型性能。

训练集表现检查：
- 首先，评估神经网络在训练集上的表现，用训练误差 J train(w ,b) 来衡量。
- 如果模型在训练集上的表现不佳（即训练误差高），这通常意味着模型存在高偏差，即模型过于简单，无法捕捉数据的复杂性。
增加网络大小：
- 当模型在训练集上的表现不佳时，可以通过增加网络的大小（例如，增加层数或每层的神经元数量）来降低偏差。
- 更大的网络通常具有更高的表达能力，能够更好地拟合训练数据。
交叉验证集表现检查：
- 一旦模型在训练集上表现良好，接下来需要评估其在交叉验证集上的表现，用交叉验证误差 J cv(w ,b) 来衡量。
- 这一步是为了检查模型是否过拟合，即在训练集上表现很好，但在未见过的数据上表现不佳。
增加数据量：
- 如果模型在交叉验证集上的表现不佳，这通常意味着模型存在高方差，即模型过于复杂，对训练数据的噪声过于敏感。
- 通过增加更多的训练数据，可以帮助模型更好地泛化，从而降低方差。
完成模型训练：
- 当模型在交叉验证集上的表现良好时，说明模型已经找到了一个合适的偏差和方差的平衡点，可以停止调整，模型训练完成。

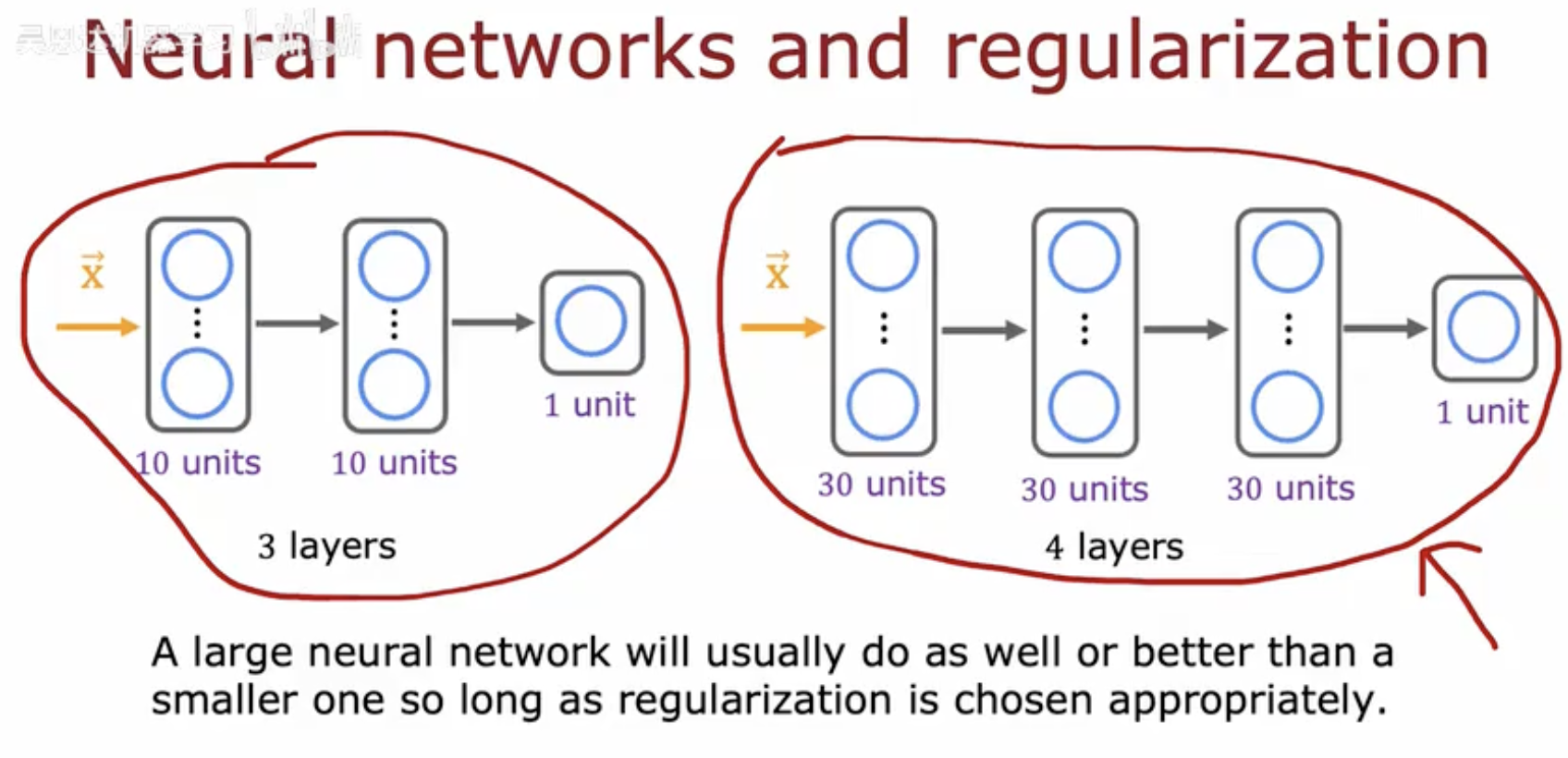
这幅图比较了两个神经网络的结构：

这幅图详细解释了如何在神经网络中实现正则化，以减少过拟合的风险。图中分为三个部分：

损失函数公式：
- 公式表示了带有正则化项的损失函数。
- 第一部分是传统的损失函数，用于衡量模型预测与实际标签之间的差异。
- 第二部分是L2正则化项，其中 λ 是正则化参数，控制正则化的强度，w 是模型的权重。
未正则化的MNIST模型：
- 该模型由三层组成：
  - 第一层（layer_1）：25个单元，使用ReLU激活函数。
  - 第二层（layer_2）：15个单元，使用ReLU激活函数。
  - 第三层（layer_3）：1个单元，使用sigmoid激活函数。
- 这个模型没有应用任何正则化技术。
正则化的MNIST模型：
- 该模型与未正则化的模型结构相同，但在每一层都应用了L2正则化。
- 每层的L2正则化系数设置为0.01，这意味着权重的平方和将被乘以0.01并添加到总损失中。
- 这种正则化有助于防止模型在训练数据上过拟合，因为它对大权重施加了惩罚，从而鼓励模型学习更小的权重。

通过这种方式，正则化可以帮助模型在新数据上表现得更好，因为它减少了模型对训练数据中噪声的敏感性。