相机与图像
针孔相机模型
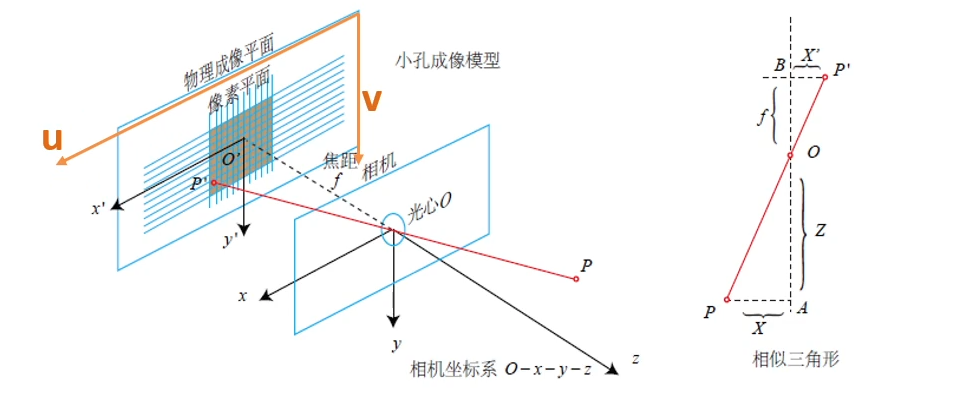
Zf=−XX′=−YY′ (像是倒立的) \frac{Z}{f}=-\frac{X}{X'}=-\frac{Y}{Y'} ~~~ (像是倒立的) fZ=−X′X=−Y′Y (像是倒立的)
坐标系
常用的坐标系一般有三种:
- 世界坐标系:描述物体在真实世界中的位置
- 相机坐标系:原点为相机光心,Z 轴指向相机前方
- 像素坐标系:原点为图像左上角,u 轴向右,v 轴向下
各个坐标系的转换关系如下:
-
世界坐标系------相机坐标系:通过旋转平移(外参)进行转换
Pc=RPw+t=TPw(使用变换矩阵T时,Pw是齐次坐标形式) P_c=RP_w+t=TP_w(使用变换矩阵T时,P_w是齐次坐标形式) Pc=RPw+t=TPw(使用变换矩阵T时,Pw是齐次坐标形式) -
相机坐标系------像素坐标系:通过内参矩 阵进行转换
(uv1)=1Z(fx0cx0fycy001)(XYZ)=1ZKPc~ \begin{pmatrix}u\\v\\1\end{pmatrix} = \frac{1}{Z}\begin{pmatrix}f_x &0 &c_x\\0 & f_y&c_y\\0&0&1\end{pmatrix}\begin{pmatrix}X\\Y\\Z\end{pmatrix}=\frac{1}{Z}K\tilde{P_c} uv1 =Z1 fx000fy0cxcy1 XYZ =Z1KPc~

畸变模型
由于透镜的存在,越靠近图像边缘的位置,畸变的现象就越明显
- 径向畸变:由透镜形状引起。可视为坐标点距离原点的长度发生了改变。桶形畸变图像的放大率随着与光轴之间的距离增加而减小,枕形畸变则相反。这两种畸变中,仅有穿过图像中心与光轴有交点的直线不变
{xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6) \begin{cases}x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{cases} {xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)
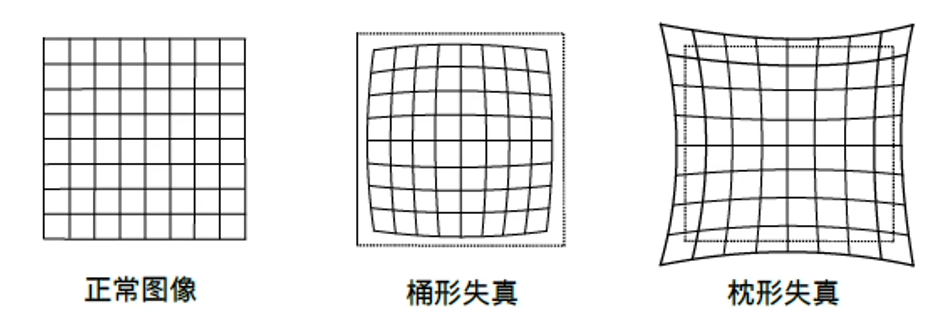
- 切向畸变 :由透镜制作和安装的缺陷引起(与成像平面不平行)。可视为坐标点水平夹角发生了改变
{xdistorted=x+2p1xy+p2(r2+2x2)ydistorted=y+p1(r2+2y2)+2p2xy \begin{cases}x_{distorted}=x+2p_1xy+p_2(r^2+2x^2)\\y_{distorted}=y+p_1(r^2+2y^2)+2p_2xy \end{cases} {xdistorted=x+2p1xy+p2(r2+2x2)ydistorted=y+p1(r2+2y2)+2p2xy
去畸变
去畸变的核心是反向映射,对于目标图像(去畸变图像)上的每一个点
- 通过内参逆变换映射到无畸变的归一化平面上,得到点 (x,y)(x,y)(x,y)
- 将该点正向代入畸变模型,计算出该点发生畸变后,在畸变的归一化平面上的对应坐标 (xdistorted,ydistorted)(x_{distorted},y_{distorted})(xdistorted,ydistorted)
- 将 (xdistorted,ydistorted)(x_{distorted},y_{distorted})(xdistorted,ydistorted) 通过内参变换,得到它在原始畸变图像上的像素坐标,并通过插值获取该位置的像素值赋给去畸变图像的对应点
内参
k=[fxscx0fycy001] k=\begin{bmatrix} f_x&s&c_x\\0&f_y&c_y\\0&0&1 \end{bmatrix} k= fx00sfy0cxcy1
- fx,fyf_x,f_yfx,fy :焦距 f 在像素坐标系u,v上的缩放。fx=fdxf_x=\frac{f}{dx}fx=dxf ,dx 是传感器上一个像素的实际物理尺寸
- cx,cyc_x,c_ycx,cy :主点。即光心在像素坐标系的投影
- sss :轴倾斜参数,描述 u 轴和 v 轴之间的夹角偏离 90∘90^\circ90∘ 的程度,通常为 0
外参
描述相机姿态,由旋转矩阵 R(3x3)和平移向量 t(3x1)组成,或者直接用变换矩阵表示
双目相机模型
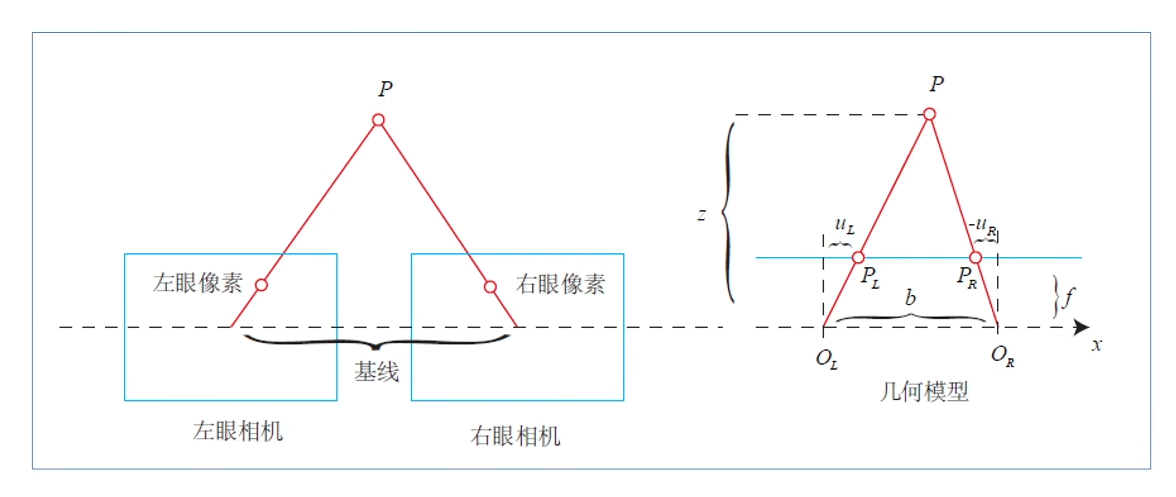
左右相机中心的距离即为基线,左右像素的几何关系如下:
z−fz=b−uL+uRb \frac{z-f}{z}=\frac{b-u_L+u_R}{b} zz−f=bb−uL+uR
整理得
z=fbdd=uL−uR z=\frac{fb}{d} \qquad d=u_L-u_R z=dfbd=uL−uR