图论简介与图神经网络
1.图论简析
传统的神经网络(如全连接网络、卷积神经网络 CNN、循环神经网络 RNN 等)大多处理规则结构的数据------
- CNN 假设数据是欧几里得网格(如图像的二维像素矩阵)
- RNN 假设数据是序列(时间步相邻)
而 图(Graph) 是一种更加通用的非欧几里得结构,由节点和边组成,可以表示社交网络、分子结构、知识图谱等。
定义:
- 图 G=(V,E)G = (V, E)G=(V,E)
- 节点集合 VVV,结点数为 ∣V∣=N|V| = N∣V∣=N
- 边集合 E⊆V×VE \subseteq V \times VE⊆V×V
- 节点特征矩阵 X∈RN×dX \in \mathbb{R}^{N \times d}X∈RN×d,每个节点有 ddd 维特征
- 邻接矩阵 A∈RN×NA \in \mathbb{R}^{N \times N}A∈RN×N,如果存在边 (i,j)(i,j)(i,j),则 Aij=1A_{ij}=1Aij=1,否则为0(可扩展为带权邻接矩阵)
1.1 基础理论
(1) 无向图(Undirected Graph)
定义
一个无向图 GGG 由一个顶点集合 VVV 和边集合 EEE 构成,记作:
G=(V,E) G = (V, E) G=(V,E)
其中:
- V={v1,v2,...,vn}V = \{ v_1, v_2, \dots, v_n \}V={v1,v2,...,vn} 表示顶点(Vertices)的集合
- E⊆{{u,v}∣u,v∈V,u≠v}E \subseteq \{ \{u, v\} \mid u, v \in V, u \neq v \}E⊆{{u,v}∣u,v∈V,u=v} 表示边(Edges)的集合。
由于无向 ,边 {u,v}\{u, v\}{u,v} 没有顺序:{u,v}={v,u}\{u, v\} = \{v, u\}{u,v}={v,u}。
(2) 有向图(Directed Graph)
定义
有向图 DDD 由顶点集合 VVV 和有向边集合 EEE 构成,记作:
D=(V,E) D = (V, E) D=(V,E)
其中:
- E⊆{(u,v)∣u,v∈V,u≠v}E \subseteq \{ (u, v) \mid u, v \in V, u \neq v \}E⊆{(u,v)∣u,v∈V,u=v}
- 这里 (u,v)(u, v)(u,v) 表示一条有向边 ,方向从 uuu 指向 vvv。
示意:
v1 → v2
↑ ↓
v3 ← v4(3) 简单图、完全图、赋权图
简单图(Simple Graph)
- 不包含自环 (u=uu=uu=u 的边)
- 不含两顶点之间的多条平行边
- 一般既可以是有向的,也可以是无向的。
完全图(Complete Graph)
- 无向完全图 KnK_nKn:任意两顶点之间都有一条边
- 边数公式:
∣E∣=n(n−1)2 |E| = \frac{n(n-1)}{2} ∣E∣=2n(n−1)
示例 :K4K_4K4 有 444 个顶点和 666 条边。
赋权图(Weighted Graph)
- 每条边附有一个权值 w:E→Rw: E \to \mathbb{R}w:E→R
- 常用于表示距离、费用、容量等。
(4) 顶点的度(Degree of a Vertex)
在无向图 G=(V,E)G = (V, E)G=(V,E) 中,顶点 vvv 的度 deg(v)\deg(v)deg(v) 定义为与 vvv 相关联的边的数量:
deg(v)=∣{u∈V∣{u,v}∈E}∣ \deg(v) = |\{ u \in V \mid \{u, v\} \in E \}| deg(v)=∣{u∈V∣{u,v}∈E}∣
在有向图中:
- 入度(In-degree) :
deg−(v)=∣{u∈V∣(u,v)∈E}∣ \deg^{-}(v) = |\{ u \in V \mid (u, v) \in E \}| deg−(v)=∣{u∈V∣(u,v)∈E}∣ - 出度(Out-degree) :
deg+(v)=∣{u∈V∣(v,u)∈E}∣ \deg^{+}(v) = |\{ u \in V \mid (v, u) \in E \}| deg+(v)=∣{u∈V∣(v,u)∈E}∣
(5) 子图与图的连通性
子图(Subgraph)
若 G′=(V′,E′)G' = (V', E')G′=(V′,E′) 满足 V′⊆VV' \subseteq VV′⊆V 且 E′⊆EE' \subseteq EE′⊆E,则称 G′G'G′ 是 GGG 的子图。
连通性(Connectivity)
- 连通图:无向图中任意两个顶点间存在至少一条路径
- 强连通图 (Strongly Connected):有向图中任意两个顶点 u,vu, vu,v,既存在从 uuu 到 vvv 的有向路径,也存在从 vvv 到 uuu 的有向路径。
- 弱连通图(Weakly Connected):把有向边忽略方向当作无向边后,该图为连通图。
(6) 矩阵表示法
邻接矩阵(Adjacency Matrix)
对于图 G=(V,E)G=(V,E)G=(V,E),顶点编号 v1,...,vnv_1,\dots,v_nv1,...,vn,邻接矩阵 AAA 为:
Aij={1若 (vi,vj)∈E 或 {vi,vj}∈E0否则 A_{ij} = \begin{cases} 1 & \text{若 } (v_i,v_j) \in E \text{ 或 } \{v_i,v_j\} \in E \\ 0 & \text{否则} \end{cases} Aij={10若 (vi,vj)∈E 或 {vi,vj}∈E否则
对于加权图,AijA_{ij}Aij 可以为边的权值,若无边则用 000 或 ∞\infty∞ 表示。
例:无向图
v1 - v2
| |
v3 - v4邻接矩阵为:
A=[0110100110010110] A = \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix} A= 0110100110010110
关联矩阵(Incidence Matrix)
设无向图 GGG 顶点为 v1,...,vnv_1,\dots,v_nv1,...,vn,边为 e1,...,eme_1,\dots,e_me1,...,em,关联矩阵 BBB 为 n×mn \times mn×m 矩阵,定义为:
无向图 :
Bij={1若顶点 vi 是边 ej 的一个端点0否则 B_{ij} = \begin{cases} 1 & \text{若顶点 } v_i \text{ 是边 } e_j \text{ 的一个端点} \\ 0 & \text{否则} \end{cases} Bij={10若顶点 vi 是边 ej 的一个端点否则
有向图 (顶点到边):
Bij={−1若 vi 是边 ej 的起点1若 vi 是边 ej 的终点0否则 B_{ij} = \begin{cases} -1 & \text{若 } v_i \text{ 是边 } e_j \text{ 的起点} \\ 1 & \text{若 } v_i \text{ 是边 } e_j \text{ 的终点} \\ 0 & \text{否则} \end{cases} Bij=⎩ ⎨ ⎧−110若 vi 是边 ej 的起点若 vi 是边 ej 的终点否则
1.2 最短路算法
(1) Dijkstra算法
Dijkstra算法是一种用于计算从单一源点到图中所有其他顶点的最短路径的算法。该算法适用于非负权重的有向图或无向图。
设图 G=(V,E)G = (V, E)G=(V,E),其中 VVV 是顶点集合,EEE 是边集合。对于边 (u,v)∈E(u, v) \in E(u,v)∈E,权重为 w(u,v)≥0w(u, v) \geq 0w(u,v)≥0。
核心思想: 贪心策略,每次选择距离源点最近的未访问顶点,并更新其邻接顶点的距离。
数学表示:
- d[v]d[v]d[v]:从源点 sss 到顶点 vvv 的最短距离
- SSS:已确定最短路径的顶点集合
- QQQ:待处理的顶点集合
松弛操作:
d[v]=min(d[v],d[u]+w(u,v))d[v] = \min(d[v], d[u] + w(u, v))d[v]=min(d[v],d[u]+w(u,v))
算法步骤
- 初始化: d[s]=0d[s] = 0d[s]=0,d[v]=∞d[v] = \inftyd[v]=∞ (对于 v≠sv \neq sv=s)
- 选择: 从 QQQ 中选择 d[u]d[u]d[u] 最小的顶点 uuu
- 松弛: 对于 uuu 的所有邻接顶点 vvv,执行松弛操作
- 更新: 将 uuu 从 QQQ 中移除,加入 SSS
- 重复: 直到 QQQ 为空
时间复杂度分析
- 朴素实现: O(V2)O(V^2)O(V2)
- 二叉堆优化: O((V+E)logV)O((V + E) \log V)O((V+E)logV)
- 斐波那契堆优化: O(VlogV+E)O(V \log V + E)O(VlogV+E)
接下来,我们将实现Dijkstra算法,并使用它来计算图中最短路径。
python
import heapq
from collections import defaultdict
import math
class Graph:
def __init__(self):
self.graph = defaultdict(list)
self.vertices = set()
def add_edge(self, u, v, weight):
"""添加边"""
self.graph[u].append((v, weight))
self.vertices.add(u)
self.vertices.add(v)
def dijkstra(self, start):
"""
Dijkstra算法实现
返回从start到所有顶点的最短距离和路径
"""
# 初始化距离字典
distances = {vertex: math.inf for vertex in self.vertices}
distances[start] = 0
# 记录路径的前驱节点
previous = {vertex: None for vertex in self.vertices}
# 优先队列,存储(距离, 顶点)
pq = [(0, start)]
visited = set()
while pq:
current_distance, current_vertex = heapq.heappop(pq)
# 如果已访问过,跳过
if current_vertex in visited:
continue
visited.add(current_vertex)
# 遍历当前顶点的所有邻接顶点
for neighbor, weight in self.graph[current_vertex]:
distance = current_distance + weight
# 松弛操作
if distance < distances[neighbor]:
distances[neighbor] = distance
previous[neighbor] = current_vertex
heapq.heappush(pq, (distance, neighbor))
return distances, previous
def get_shortest_path(self, previous, start, end):
"""根据前驱节点重构最短路径"""
path = []
current = end
while current is not None:
path.append(current)
current = previous[current]
path.reverse()
# 检查路径是否有效
if path[0] == start:
return path
else:
return None # 无法到达
if __name__ == "__main__":
"""Dijkstra算法示例"""
g = Graph()
# 构建示例图
edges = [
('A', 'B', 4), ('A', 'C', 2),
('B', 'C', 1), ('B', 'D', 5),
('C', 'D', 8), ('C', 'E', 10),
('D', 'E', 2)
]
for u, v, w in edges:
g.add_edge(u, v, w)
# 计算从A到所有顶点的最短路径
distances, previous = g.dijkstra('A')
print("=== Dijkstra算法结果 ===")
print("从顶点A到各顶点的最短距离:")
for vertex in sorted(distances.keys()):
if distances[vertex] == math.inf:
print(f"A -> {vertex}: 不可达")
else:
path = g.get_shortest_path(previous, 'A', vertex)
print(f"A -> {vertex}: 距离={distances[vertex]}, 路径={' -> '.join(path)}")=== Dijkstra算法结果 ===
从顶点A到各顶点的最短距离:
A -> A: 距离=0, 路径=A
A -> B: 距离=4, 路径=A -> B
A -> C: 距离=2, 路径=A -> C
A -> D: 距离=9, 路径=A -> B -> D
A -> E: 距离=11, 路径=A -> B -> D -> E(2) Floyd算法
Floyd-Warshall算法是一种用于计算图中所有顶点对之间最短路径的动态规划算法。该算法可以处理负权重边,但不能处理负权重环。
核心思想: 动态规划,通过逐步考虑中间顶点来更新最短路径。
状态定义:
dij(k)=从顶点 i 到顶点 j 且只经过顶点 {1,2,...,k} 的最短路径长度d_{ij}^{(k)} = \text{从顶点 } i \text{ 到顶点 } j \text{ 且只经过顶点 } \{1, 2, ..., k\} \text{ 的最短路径长度}dij(k)=从顶点 i 到顶点 j 且只经过顶点 {1,2,...,k} 的最短路径长度
状态转移方程:
dij(k)=min(dij(k−1),dik(k−1)+dkj(k−1))d_{ij}^{(k)} = \min(d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)})dij(k)=min(dij(k−1),dik(k−1)+dkj(k−1))
初始状态:
dij(0)={0if i=jw(i,j)if (i,j)∈E∞otherwised_{ij}^{(0)} = \begin{cases} 0 & \text{if } i = j \\ w(i,j) & \text{if } (i,j) \in E \\ \infty & \text{otherwise} \end{cases}dij(0)=⎩ ⎨ ⎧0w(i,j)∞if i=jif (i,j)∈Eotherwise
算法步骤
- 初始化: 构建距离矩阵 D(0)D^{(0)}D(0)
- 迭代: 对于 k=1,2,...,nk = 1, 2, ..., nk=1,2,...,n
- 对于所有顶点对 (i,j)(i, j)(i,j)
- 更新 dij(k)=min(dij(k−1),dik(k−1)+dkj(k−1))d_{ij}^{(k)} = \min(d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)})dij(k)=min(dij(k−1),dik(k−1)+dkj(k−1))
- 结果: D(n)D^{(n)}D(n) 即为所有顶点对的最短距离矩阵
时间复杂度分析
- 时间复杂度: O(V3)O(V^3)O(V3)
- 空间复杂度: O(V2)O(V^2)O(V2)
接下来,我们将实现Floyd-Warshall算法,并使用它来计算图中最短路径。
python
import math
class FloydWarshall:
def __init__(self, vertices):
"""
初始化Floyd-Warshall算法
vertices: 顶点列表
"""
self.vertices = vertices
self.n = len(vertices)
self.vertex_to_index = {v: i for i, v in enumerate(vertices)}
# 初始化距离矩阵
self.dist = [[math.inf for _ in range(self.n)] for _ in range(self.n)]
self.next = [[None for _ in range(self.n)] for _ in range(self.n)]
# 对角线元素为0
for i in range(self.n):
self.dist[i][i] = 0
def add_edge(self, u, v, weight):
"""添加边"""
i = self.vertex_to_index[u]
j = self.vertex_to_index[v]
self.dist[i][j] = weight
self.next[i][j] = j
def floyd_warshall(self):
"""
Floyd-Warshall算法实现
计算所有顶点对之间的最短路径
"""
# 三重循环:k为中间顶点,i为起点,j为终点
for k in range(self.n):
for i in range(self.n):
for j in range(self.n):
# 松弛操作
if self.dist[i][k] + self.dist[k][j] < self.dist[i][j]:
self.dist[i][j] = self.dist[i][k] + self.dist[k][j]
self.next[i][j] = self.next[i][k]
def get_shortest_distance(self, u, v):
"""获取两点间最短距离"""
i = self.vertex_to_index[u]
j = self.vertex_to_index[v]
return self.dist[i][j]
def get_shortest_path(self, u, v):
"""重构最短路径"""
i = self.vertex_to_index[u]
j = self.vertex_to_index[v]
if self.dist[i][j] == math.inf:
return None
path = [i]
while i != j:
i = self.next[i][j]
if i is None:
return None
path.append(i)
# 转换索引为顶点名称
return [self.vertices[idx] for idx in path]
def print_distance_matrix(self):
"""打印距离矩阵"""
print("\n=== 最短距离矩阵 ===")
print(" ", end="")
for v in self.vertices:
print(f"{v:>6}", end="")
print()
for i, u in enumerate(self.vertices):
print(f"{u:>4} ", end="")
for j in range(self.n):
if self.dist[i][j] == math.inf:
print(" ∞ ", end="")
else:
print(f"{self.dist[i][j]:>6.1f}", end="")
print()
def detect_negative_cycle(self):
"""检测负权重环"""
for i in range(self.n):
if self.dist[i][i] < 0:
return True
return False
if __name__ == "__main__":
"""Floyd算法示例"""
vertices = ['A', 'B', 'C', 'D']
fw = FloydWarshall(vertices)
# 添加边
edges = [
('A', 'B', 3), ('A', 'C', 8), ('A', 'D', 7),
('B', 'A', 3), ('B', 'C', 2),
('C', 'A', 8), ('C', 'B', 2), ('C', 'D', 1),
('D', 'A', 7), ('D', 'C', 1)
]
for u, v, w in edges:
fw.add_edge(u, v, w)
print("=== Floyd-Warshall算法示例 ===")
print("原始图的边:")
for u, v, w in edges:
print(f"{u} -> {v}: {w}")
# 执行Floyd算法
fw.floyd_warshall()
# 检测负权重环
if fw.detect_negative_cycle():
print("警告: 图中存在负权重环!")
# 打印距离矩阵
fw.print_distance_matrix()
# 打印所有顶点对的最短路径
print("\n=== 所有顶点对的最短路径 ===")
for i, u in enumerate(vertices):
for j, v in enumerate(vertices):
if i != j:
distance = fw.get_shortest_distance(u, v)
path = fw.get_shortest_path(u, v)
if path:
print(f"{u} -> {v}: 距离={distance}, 路径={' -> '.join(path)}")
else:
print(f"{u} -> {v}: 不可达")=== Floyd-Warshall算法示例 ===
原始图的边:
A -> B: 3
A -> C: 8
A -> D: 7
B -> A: 3
B -> C: 2
C -> A: 8
C -> B: 2
C -> D: 1
D -> A: 7
D -> C: 1
=== 最短距离矩阵 ===
A B C D
A 0.0 3.0 5.0 6.0
B 3.0 0.0 2.0 3.0
C 5.0 2.0 0.0 1.0
D 6.0 3.0 1.0 0.0
=== 所有顶点对的最短路径 ===
A -> B: 距离=3, 路径=A -> B
A -> C: 距离=5, 路径=A -> B -> C
A -> D: 距离=6, 路径=A -> B -> C -> D
B -> A: 距离=3, 路径=B -> A
B -> C: 距离=2, 路径=B -> C
B -> D: 距离=3, 路径=B -> C -> D
C -> A: 距离=5, 路径=C -> B -> A
C -> B: 距离=2, 路径=C -> B
C -> D: 距离=1, 路径=C -> D
D -> A: 距离=6, 路径=D -> C -> B -> A
D -> B: 距离=3, 路径=D -> C -> B
D -> C: 距离=1, 路径=D -> C(3) 算法比较
| 特性 | Dijkstra | Floyd-Warshall |
|---|---|---|
| 适用场景 | 单源最短路径 | 所有顶点对最短路径 |
| 权重要求 | 非负权重 | 可处理负权重(无负环) |
| 时间复杂度 | O(V2)O(V^2)O(V2) 或 O((V+E)logV)O((V+E)\log V)O((V+E)logV) | O(V3)O(V^3)O(V3) |
| 空间复杂度 | O(V)O(V)O(V) | O(V2)O(V^2)O(V2) |
| 实现难度 | 中等 | 简单 |
图神经网络(Graph Neural Network, GNN)
图神经网络(GNN)简介
1. 为什么需要图神经网络?
在深度学习领域,卷积神经网络(CNN)和循环神经网络(RNN)等模型取得了巨大成功。然而,它们主要处理的是欧几里得空间中的数据。
- CNN 处理图像,可以看作是二维或三维的规则网格(Grid)。
- RNN 处理序列数据,可以看作是一维的线性序列。
这些数据的共同特点是结构规整、有固定的邻居关系和顺序。但是,现实世界中存在大量非欧几里得空间 的数据,它们以 图(Graph) 的形式存在,例如:
- 社交网络:用户是节点,关注关系是边。
- 分子结构:原子是节点,化学键是边。
- 知识图谱:实体是节点,关系是边。
- 交通网络:路口是节点,道路是边。
这些图结构数据具有以下特点,使得传统深度学习模型难以直接应用:
- 任意的邻居数量:每个节点的邻居(度)数量不固定。
- 无序性:节点的邻居没有自然的排列顺序。
- 复杂的拓扑结构:图的连接方式千变万化,不是规整的网格。
图神经网络(GNN) 应运而生,其核心目标是设计一种能够直接在图结构数据上运行,并有效学习其特征和模式的神经网络模型。
2. GNN 的核心思想:消息传递(Message Passing)
GNN 的核心思想可以概括为 邻域聚合(Neighborhood Aggregation) 或 消息传递(Message Passing) 。这个思想非常直观:一个节点的最新表示(特征),应该由其自身的当前表示和其所有邻居节点的表示共同决定。
可以想象成社交网络中的信息传播:你的想法和观点,不仅受你自己的影响,也受到你朋友们(邻居)想法的影响。GNN 就是在模拟这个过程。
通过多轮消息传递,每个节点能够聚合到越来越远邻居的信息:
- 1 轮:聚合直接邻居(1-hop)的信息。
- 2 轮:聚合邻居的邻居(2-hop)的信息。
- k 轮:聚合 k-hop 范围内的邻居信息。
这样,GNN 最终为每个节点学习到的节点嵌入(Node Embedding),就同时编码了该节点的自身特征以及其在图中的局部拓扑结构信息。
3. GNN 的通用工作流程
一个典型的 GNN 模型包含多个 GNN 层,其工作流程可以分为以下几个步骤。我们用数学公式来形式化这个过程。
假设我们有一个图 G=(V,E)G=(V, E)G=(V,E),其中 VVV 是节点集合,EEE 是边集合。
- 每个节点 v∈Vv \in Vv∈V 都有一个初始特征向量 xvx_vxv。
- 我们将第 kkk 层的节点 vvv 的特征向量(或称为"隐藏状态")记为 hv(k)h_v^{(k)}hv(k)。
- 初始状态 hv(0)=xvh_v^{(0)} = x_vhv(0)=xv。
步骤一:消息聚合与更新 (Aggregation & Update)
这是 GNN 的核心。在第 kkk 层,对于图中的每一个节点 vvv,GNN 会执行以下两步操作来计算其新的特征向量 hv(k)h_v^{(k)}hv(k):
-
聚合(AGGREGATE) :从节点 vvv 的邻居集合 N(v)\mathcal{N}(v)N(v) 中收集信息。具体来说,就是将所有邻居节点在第 k−1k-1k−1 层的特征向量 hu(k−1)h_u^{(k-1)}hu(k−1)(其中 u∈N(v)u \in \mathcal{N}(v)u∈N(v))通过一个聚合函数(如求和、求均值、求最大值等)汇集成一条消息 mN(v)(k)m_{\mathcal{N}(v)}^{(k)}mN(v)(k)。
mN(v)(k)=AGGREGATE(k)({hu(k−1):u∈N(v)})m_{\mathcal{N}(v)}^{(k)} = \text{AGGREGATE}^{(k)} \left( \left\{ h_u^{(k-1)} : u \in \mathcal{N}(v) \right\} \right)mN(v)(k)=AGGREGATE(k)({hu(k−1):u∈N(v)})
-
更新(UPDATE) :将聚合到的邻居消息 mN(v)(k)m_{\mathcal{N}(v)}^{(k)}mN(v)(k) 与节点 vvv 自身在第 k−1k-1k−1 层的特征向量 hv(k−1)h_v^{(k-1)}hv(k−1) 结合起来,通过一个更新函数(通常是一个神经网络层)来生成节点 vvv 在第 kkk 层的新特征向量 hv(k)h_v^{(k)}hv(k)。
hv(k)=UPDATE(k)(hv(k−1),mN(v)(k))h_v^{(k)} = \text{UPDATE}^{(k)} \left( h_v^{(k-1)}, m_{\mathcal{N}(v)}^{(k)} \right)hv(k)=UPDATE(k)(hv(k−1),mN(v)(k))
这个过程会在所有节点上并行执行,并重复 KKK 轮(即堆叠 KKK 个 GNN 层)。
步骤二:图级别读出 (Graph-level Readout)
经过 KKK 轮消息传递后,我们得到了图中每个节点的最终特征表示 hv(K)h_v^{(K)}hv(K)。根据下游任务的不同,我们可能需要对图进行整体的预测:
-
节点级别任务 (如节点分类):直接使用最终的节点表示 hv(K)h_v^{(K)}hv(K) 进行预测。
-
边级别任务 (如链接预测):将边的两个端点的最终表示 hu(K)h_u^{(K)}hu(K) 和 hv(K)h_v^{(K)}hv(K) 结合起来进行预测。
-
图级别任务 (如分子属性预测):需要一个**读出(READOUT)**函数,将图中所有节点的最终表示聚合成一个唯一的、固定大小的图级别表示 hGh_GhG。
hG=READOUT({hv(K)∣v∈V})h_G = \text{READOUT} \left( \left\{ h_v^{(K)} \mid v \in V \right\} \right)hG=READOUT({hv(K)∣v∈V})
常见的 READOUT 函数包括对所有节点向量求和、求均值或求最大值。
接下来,我们通过一个代码实例来展示 GNN 的具体实现。首先,我们需要导入一些必要的库,并创建一个简单的图作为演示。
python
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from typing import Dict, List, Callable
import warnings
warnings.filterwarnings('ignore')
print("导入库完成!")
# 创建一个简单的图作为演示
def create_sample_graph():
"""创建一个包含6个节点的示例图"""
G = nx.Graph()
# 添加节点和边
edges = [(0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 0), (1, 4)]
G.add_edges_from(edges)
# 为每个节点分配初始特征向量 (3维特征)
node_features = {
0: np.array([1.0, 0.5, 0.2]),
1: np.array([0.8, 1.0, 0.3]),
2: np.array([0.6, 0.7, 1.0]),
3: np.array([1.0, 0.2, 0.8]),
4: np.array([0.4, 0.9, 0.6]),
5: np.array([0.7, 0.4, 0.9])
}
return G, node_features
# 创建图和节点特征
G, initial_features = create_sample_graph()
print(f"图的基本信息:")
print(f"节点数量: {G.number_of_nodes()}")
print(f"边数量: {G.number_of_edges()}")
print(f"特征维度: {len(list(initial_features.values())[0])}")
# 可视化图结构
plt.figure(figsize=(8, 6))
pos = nx.spring_layout(G, seed=42)
nx.draw(G, pos, with_labels=True, node_color='lightblue',
node_size=500, font_size=16, font_weight='bold')
plt.title("Graph Visualization")
plt.show()
# 显示初始节点特征
print("\n初始节点特征:")
for node, features in initial_features.items():
print(f"节点 {node}: {features}")导入库完成!
图的基本信息:
节点数量: 6
边数量: 7
特征维度: 3
初始节点特征:
节点 0: [1. 0.5 0.2]
节点 1: [0.8 1. 0.3]
节点 2: [0.6 0.7 1. ]
节点 3: [1. 0.2 0.8]
节点 4: [0.4 0.9 0.6]
节点 5: [0.7 0.4 0.9]接下来,我们将实现一个简单的 GNN 模型,该模型包含多个 GNN 层,并使用消息传递机制来更新节点的特征。
下方代码定义了一个简单的图神经网络(GNN)类,用于对图结构数据进行学习和特征更新。整个类的核心思想是通过多层消息传递机制,让每个节点不断聚合其邻居的信息并更新自身的特征表示。初始化时,网络根据输入特征维度、隐藏层维度和网络层数设置相应的权重参数,每一层都包含用于处理自身特征和邻居特征的权重矩阵以及偏置项,这些参数通过随机初始化为后续的特征变换提供基础。
该GNN模型的关键功能分为三个部分:聚合、更新和前向传播。聚合函数负责将一个节点所有邻居的特征信息整合成一个统一的消息向量,支持均值、求和和最大值三种方式,从而捕捉邻居的整体特征。更新函数则结合节点自身的特征和从邻居聚合而来的信息,通过线性变换和非线性激活函数(ReLU)生成新的节点特征,实现信息的融合与抽象。前向传播一层函数将上述两个步骤应用于图中的每一个节点,逐个计算其在当前层的输出特征,并打印中间过程,便于观察特征演化。
python
class SimpleGNN:
def __init__(self, input_dim: int, hidden_dim: int, num_layers: int = 2):
"""
简单的GNN实现
Args:
input_dim: 输入特征维度
hidden_dim: 隐藏层维度
num_layers: GNN层数
"""
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.num_layers = num_layers
# 初始化权重矩阵 (简化版本,实际中会使用更复杂的初始化)
np.random.seed(42) # 为了结果可复现
self.weights = []
for i in range(num_layers):
if i == 0:
# 第一层:从输入维度到隐藏维度
W_self = np.random.randn(input_dim, hidden_dim) * 0.1
W_neighbor = np.random.randn(input_dim, hidden_dim) * 0.1
else:
# 后续层:隐藏维度到隐藏维度
W_self = np.random.randn(hidden_dim, hidden_dim) * 0.1
W_neighbor = np.random.randn(hidden_dim, hidden_dim) * 0.1
self.weights.append({
'W_self': W_self,
'W_neighbor': W_neighbor,
'bias': np.random.randn(hidden_dim) * 0.01
})
def aggregate(self, neighbor_features: List[np.ndarray], method: str = 'mean') -> np.ndarray:
"""
聚合函数:AGGREGATE步骤
Args:
neighbor_features: 邻居节点特征列表
method: 聚合方法 ('mean', 'sum', 'max')
Returns:
聚合后的消息向量
"""
if len(neighbor_features) == 0:
return np.zeros(self.hidden_dim if hasattr(self, 'hidden_dim') else len(neighbor_features[0]))
neighbor_matrix = np.stack(neighbor_features, axis=0)
if method == 'mean':
return np.mean(neighbor_matrix, axis=0)
elif method == 'sum':
return np.sum(neighbor_matrix, axis=0)
elif method == 'max':
return np.max(neighbor_matrix, axis=0)
else:
raise ValueError(f"Unknown aggregation method: {method}")
def update(self, self_features: np.ndarray, neighbor_message: np.ndarray,
layer_idx: int) -> np.ndarray:
"""
更新函数:UPDATE步骤
Args:
self_features: 节点自身特征
neighbor_message: 聚合的邻居消息
layer_idx: 当前层索引
Returns:
更新后的节点特征
"""
W_self = self.weights[layer_idx]['W_self']
W_neighbor = self.weights[layer_idx]['W_neighbor']
bias = self.weights[layer_idx]['bias']
# 线性变换
self_transform = np.dot(self_features, W_self)
neighbor_transform = np.dot(neighbor_message, W_neighbor)
# 组合并添加偏置
combined = self_transform + neighbor_transform + bias
# 应用ReLU激活函数
return np.maximum(0, combined)
def forward_layer(self, graph: nx.Graph, node_features: Dict[int, np.ndarray],
layer_idx: int) -> Dict[int, np.ndarray]:
"""
前向传播一层
Args:
graph: 图结构
node_features: 当前层节点特征
layer_idx: 层索引
Returns:
下一层的节点特征
"""
new_features = {}
print(f"\n=== 第 {layer_idx + 1} 层前向传播 ===")
for node in graph.nodes():
# 获取邻居节点
neighbors = list(graph.neighbors(node))
print(f"\n节点 {node}:")
print(f" 邻居节点: {neighbors}")
# 步骤1: 聚合邻居特征 (AGGREGATE)
neighbor_features = [node_features[neighbor] for neighbor in neighbors]
neighbor_message = self.aggregate(neighbor_features, method='mean')
print(f" 聚合后的邻居消息: {neighbor_message[:3]}...") # 只显示前3个元素
# 步骤2: 更新节点特征 (UPDATE)
new_features[node] = self.update(
node_features[node],
neighbor_message,
layer_idx
)
print(f" 更新后特征: {new_features[node][:3]}...") # 只显示前3个元素
return new_features
print("GNN类定义完成!")GNN类定义完成!接下来,我们将初始化一个简单的图结构,并展示如何使用GNN模型进行节点特征更新和图级别读出。
python
# ==================== 初始化GNN模型并展示第一层计算 ====================
# 初始化GNN模型
input_dim = 3 # 输入特征维度
hidden_dim = 4 # 隐藏层维度
num_layers = 2 # 层数
gnn_model = SimpleGNN(input_dim, hidden_dim, num_layers)
print("GNN模型初始化完成!")
print(f"输入维度: {input_dim}")
print(f"隐藏维度: {hidden_dim}")
print(f"层数: {num_layers}")
# 设置初始特征 h^(0) = x_v
current_features = initial_features.copy()
print(f"\n初始特征 h^(0):")
for node, features in current_features.items():
print(f"节点 {node}: {features}")GNN模型初始化完成!
输入维度: 3
隐藏维度: 4
层数: 2
初始特征 h^(0):
节点 0: [1. 0.5 0.2]
节点 1: [0.8 1. 0.3]
节点 2: [0.6 0.7 1. ]
节点 3: [1. 0.2 0.8]
节点 4: [0.4 0.9 0.6]
节点 5: [0.7 0.4 0.9]
python
# ==================== 执行第一层GNN计算 ====================
# 执行第一层前向传播
layer_1_features = gnn_model.forward_layer(G, current_features, layer_idx=0)
print(f"\n第一层输出特征 h^(1) (维度: {hidden_dim}):")
for node, features in layer_1_features.items():
print(f"节点 {node}: {features}")=== 第 1 层前向传播 ===
节点 0:
邻居节点: [1, 5]
聚合后的邻居消息: [0.75 0.7 0.6 ]...
更新后特征: [0.05831835 0. 0. ]...
节点 1:
邻居节点: [0, 2, 4]
聚合后的邻居消息: [0.66666667 0.7 0.6 ]...
更新后特征: [0.0299653 0. 0.00981938]...
节点 2:
邻居节点: [1, 3]
聚合后的邻居消息: [0.9 0.6 0.55]...
更新后特征: [0.00263827 0. 0. ]...
节点 3:
邻居节点: [2, 4]
聚合后的邻居消息: [0.5 0.8 0.8]...
更新后特征: [0.0503101 0. 0. ]...
节点 4:
邻居节点: [3, 5, 1]
聚合后的邻居消息: [0.83333333 0.53333333 0.66666667]...
更新后特征: [0.02903825 0. 0. ]...
节点 5:
邻居节点: [4, 0]
聚合后的邻居消息: [0.7 0.7 0.4]...
更新后特征: [0. 0. 0.]...
第一层输出特征 h^(1) (维度: 4):
节点 0: [0.05831835 0. 0. 0. ]
节点 1: [0.0299653 0. 0.00981938 0. ]
节点 2: [0.00263827 0. 0. 0. ]
节点 3: [0.0503101 0. 0. 0. ]
节点 4: [0.02903825 0. 0. 0. ]
节点 5: [0. 0. 0. 0.]
python
# ==================== 执行第二层GNN计算 ====================
# 执行第二层前向传播
layer_2_features = gnn_model.forward_layer(G, layer_1_features, layer_idx=1)
print(f"\n第二层输出特征 h^(2) (最终节点表示):")
for node, features in layer_2_features.items():
print(f"节点 {node}: {features}")
# 保存最终节点特征
final_node_features = layer_2_features=== 第 2 层前向传播 ===
节点 0:
邻居节点: [1, 5]
聚合后的邻居消息: [0.01498265 0. 0.00490969]...
更新后特征: [0. 0. 0.]...
节点 1:
邻居节点: [0, 2, 4]
聚合后的邻居消息: [0.02999829 0. 0. ]...
更新后特征: [0. 0. 0.]...
节点 2:
邻居节点: [1, 3]
聚合后的邻居消息: [0.0401377 0. 0.00490969]...
更新后特征: [0. 0. 0.]...
节点 3:
邻居节点: [2, 4]
聚合后的邻居消息: [0.01583826 0. 0. ]...
更新后特征: [0. 0. 0.]...
节点 4:
邻居节点: [3, 5, 1]
聚合后的邻居消息: [0.02675847 0. 0.00327313]...
更新后特征: [0. 0. 0.]...
节点 5:
邻居节点: [4, 0]
聚合后的邻居消息: [0.0436783 0. 0. ]...
更新后特征: [0. 0. 0.]...
第二层输出特征 h^(2) (最终节点表示):
节点 0: [0. 0. 0. 0.00088119]
节点 1: [0. 0. 0. 0.]
节点 2: [0. 0. 0. 0.]
节点 3: [0. 0. 0. 0.]
节点 4: [0. 0. 0. 0.]
节点 5: [0. 0. 0. 0.]
python
# ==================== 实现图级别读出函数 (Graph-level Readout) ====================
class GraphReadout:
@staticmethod
def readout(node_features: Dict[int, np.ndarray], method: str = 'mean') -> np.ndarray:
"""
图级别读出函数:将所有节点特征聚合为图级别表示
Args:
node_features: 节点特征字典
method: 聚合方法 ('mean', 'sum', 'max')
Returns:
图级别特征表示
"""
feature_matrix = np.stack(list(node_features.values()), axis=0)
if method == 'mean':
return np.mean(feature_matrix, axis=0)
elif method == 'sum':
return np.sum(feature_matrix, axis=0)
elif method == 'max':
return np.max(feature_matrix, axis=0)
else:
raise ValueError(f"Unknown readout method: {method}")
# 演示不同的读出方法
readout = GraphReadout()
print("=== 图级别读出 (Graph-level Readout) ===")
print(f"输入: 所有节点的最终特征 h_v^(K)")
graph_repr_mean = readout.readout(final_node_features, method='mean')
graph_repr_sum = readout.readout(final_node_features, method='sum')
graph_repr_max = readout.readout(final_node_features, method='max')
print(f"\n使用不同聚合方法的图级别表示:")
print(f"平均值 (Mean): {graph_repr_mean}")
print(f"求和 (Sum): {graph_repr_sum}")
print(f"最大值 (Max): {graph_repr_max}")=== 图级别读出 (Graph-level Readout) ===
输入: 所有节点的最终特征 h_v^(K)
使用不同聚合方法的图级别表示:
平均值 (Mean): [0. 0. 0. 0.00014687]
求和 (Sum): [0. 0. 0. 0.00088119]
最大值 (Max): [0. 0. 0. 0.00088119]
python
# ==================== 展示不同任务类型的应用 ====================
def demonstrate_downstream_tasks(graph: nx.Graph, final_features: Dict[int, np.ndarray]):
"""演示GNN在不同下游任务中的应用"""
print("=== 下游任务演示 ===")
# 1. 节点级别任务 (Node-level Task)
print("\n1. 节点级别任务 (如节点分类):")
print(" 直接使用最终节点表示进行预测")
# 模拟节点分类:使用简单的线性分类器
np.random.seed(42)
classifier_weights = np.random.randn(len(final_features[0]), 2) # 2类分类
for node_id in [0, 1, 2]: # 只展示前3个节点
node_features = final_features[node_id]
logits = np.dot(node_features, classifier_weights)
probabilities = np.exp(logits) / np.sum(np.exp(logits)) # softmax
predicted_class = np.argmax(probabilities)
print(f" 节点 {node_id}: 预测类别 = {predicted_class}, " +
f"概率 = [{probabilities[0]:.3f}, {probabilities[1]:.3f}]")
# 2. 边级别任务 (Edge-level Task)
print("\n2. 边级别任务 (如链接预测):")
print(" 结合边两端节点的特征进行预测")
# 选择几条边进行演示
sample_edges = [(0, 1), (2, 3), (1, 4)]
for edge in sample_edges:
node_u, node_v = edge
# 简单的边特征:两个节点特征的拼接
edge_features = np.concatenate([final_features[node_u], final_features[node_v]])
# 模拟链接预测分数 (简化版本)
link_score = np.dot(final_features[node_u], final_features[node_v])
print(f" 边 ({node_u}, {node_v}): 链接分数 = {link_score:.3f}")
# 3. 图级别任务 (Graph-level Task)
print("\n3. 图级别任务 (如图分类/图属性预测):")
print(" 使用图级别表示进行预测")
# 使用之前计算的图级别表示
graph_features = readout.readout(final_features, method='mean')
# 模拟图分类
graph_classifier_weights = np.random.randn(len(graph_features), 3) # 3类分类
graph_logits = np.dot(graph_features, graph_classifier_weights)
graph_probabilities = np.exp(graph_logits) / np.sum(np.exp(graph_logits))
predicted_graph_class = np.argmax(graph_probabilities)
print(f" 图级别预测: 类别 = {predicted_graph_class}")
print(f" 类别概率: {graph_probabilities}")
# 演示不同任务
demonstrate_downstream_tasks(G, final_node_features)=== 下游任务演示 ===
1. 节点级别任务 (如节点分类):
直接使用最终节点表示进行预测
节点 0: 预测类别 = 0, 概率 = [0.500, 0.500]
节点 1: 预测类别 = 0, 概率 = [0.500, 0.500]
节点 2: 预测类别 = 0, 概率 = [0.500, 0.500]
2. 边级别任务 (如链接预测):
结合边两端节点的特征进行预测
边 (0, 1): 链接分数 = 0.000
边 (2, 3): 链接分数 = 0.000
边 (1, 4): 链接分数 = 0.000
3. 图级别任务 (如图分类/图属性预测):
使用图级别表示进行预测
图级别预测: 类别 = 0
类别概率: [0.33338145 0.33332162 0.33329693]经典 GNN 模型实例
不同的 GNN 模型,其核心区别就在于如何具体实现 AGGREGATE 和 UPDATE 函数。
(1) 图卷积网络 (GCN - Graph Convolutional Network)
GCN 是最经典的模型之一,它简化了聚合与更新步骤。其核心传播规则如下:
H(k)=σ(D^−12A^D^−12H(k−1)W(k))H^{(k)} = \sigma \left( \hat{D}^{-\frac{1}{2}} \hat{A} \hat{D}^{-\frac{1}{2}} H^{(k-1)} W^{(k)} \right)H(k)=σ(D^−21A^D^−21H(k−1)W(k))
让我们来拆解这个公式:
- H(k)H^{(k)}H(k):第 kkk 层所有节点的特征矩阵,每一行是一个节点的特征向量。
- AAA:图的邻接矩阵。Aij=1A_{ij}=1Aij=1 表示节点 iii 和 jjj 之间有边。
- III:单位矩阵。
- A^=A+I\hat{A} = A + IA^=A+I:给图的每个节点增加一个自环(self-loop),这样在聚合邻居信息时,也能包含节点自身的信息。
- D^\hat{D}D^:A^\hat{A}A^ 的度矩阵,是一个对角矩阵,D^ii=∑jA^ij\hat{D}{ii} = \sum_j \hat{A}{ij}D^ii=∑jA^ij。
- D^−12A^D^−12\hat{D}^{-\frac{1}{2}} \hat{A} \hat{D}^{-\frac{1}{2}}D^−21A^D^−21:这是 GCN 的核心,一个对称归一化的邻接矩阵 。
- 乘以 A^\hat{A}A^ 相当于对邻居特征进行求和(聚合)。
- 左右两边乘以 D^−12\hat{D}^{-\frac{1}{2}}D^−21 是为了进行归一化,可以防止节点度数高而导致特征向量尺度过大,保持数值稳定性,其效果类似于对邻居特征求加权平均。
- W(k)W^{(k)}W(k):第 kkk 层的可训练权重矩阵,相当于一个标准的全连接层。
- σ\sigmaσ:非线性激活函数,如 ReLU。
GCN 的聚合与更新 :GCN 将聚合与更新合并为一步。对于单个节点 vvv,其更新规则可以看作:
hv(k)=σ(W(k)∑u∈N(v)∪{v}1deg(v)deg(u)hu(k−1))h_v^{(k)} = \sigma \left( W^{(k)} \sum_{u \in \mathcal{N}(v) \cup \{v\}} \frac{1}{\sqrt{\deg(v)\deg(u)}} h_u^{(k-1)} \right)hv(k)=σ(W(k)∑u∈N(v)∪{v}deg(v)deg(u) 1hu(k−1))
这里,聚合函数是加权求和 ,更新函数是线性变换后接激活函数。
下边我们将从零开始实现一个图卷积网络,并在cora数据集上进行节点分类任务。
python
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
import networkx as nx
from sklearn.manifold import TSNE
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
# 设置随机种子以确保结果可复现
torch.manual_seed(42)
np.random.seed(42)
print("PyTorch版本:", torch.__version__)PyTorch版本: 2.8.0+cu126我们使用图数据集cora,它是一个常用的图分类数据集,包含2708个节点和7个节点类别。
python
from torch_geometric.datasets import Planetoid
import torch_geometric.transforms as T
def load_cora_dataset():
"""
下载并加载Cora数据集
"""
# 下载Cora数据集
dataset = Planetoid(root='/tmp/Cora', name='Cora', transform=T.NormalizeFeatures())
data = dataset[0]
return data
def convert_cora_to_synthetic_format():
"""
将Cora数据集转换为合成数据的格式
"""
# 加载Cora数据
cora_data = load_cora_dataset()
# 提取特征矩阵 (2708 nodes, 1433 features)
X = cora_data.x # 节点特征矩阵 [num_nodes, num_features]
# 创建邻接矩阵
# 从边索引创建邻接矩阵
num_nodes = X.shape[0]
A = torch.zeros(num_nodes, num_nodes)
# 填充邻接矩阵 - Cora是无向图
edge_index = cora_data.edge_index
for i in range(edge_index.shape[1]):
source, target = edge_index[0, i].item(), edge_index[1, i].item()
A[source, target] = 1
A[target, source] = 1 # 无向图
# 提取标签
y = cora_data.y # 将one-hot编码转换为类别索引
# 提取训练/验证/测试掩码
train_mask = cora_data.train_mask
val_mask = cora_data.val_mask
test_mask = cora_data.test_mask
print(f"Cora数据集信息:")
print(f"节点数: {X.shape[0]}")
print(f"特征维度: {X.shape[1]}")
print(f"类别数: {len(torch.unique(y))}")
print(f"边数: {edge_index.shape[1]}")
print(f"训练节点数: {train_mask.sum().item()}")
print(f"验证节点数: {val_mask.sum().item()}")
print(f"测试节点数: {test_mask.sum().item()}")
return X, A, y, train_mask, val_mask, test_mask
# 创建数据
X, A, y, train_mask, val_mask, test_mask = convert_cora_to_synthetic_format()
print(f"节点数量: {X.shape[0]}")
print(f"特征维度: {X.shape[1]}")
print(f"类别数量: {len(torch.unique(y))}")
print(f"边数量: {int(A.sum() / 2)}")
print(f"训练节点: {train_mask.sum()}")
print(f"验证节点: {val_mask.sum()}")
print(f"测试节点: {test_mask.sum()}")Cora数据集信息:
节点数: 2708
特征维度: 1433
类别数: 7
边数: 10556
训练节点数: 140
验证节点数: 500
测试节点数: 1000
节点数量: 2708
特征维度: 1433
类别数量: 7
边数量: 5278
训练节点: 140
验证节点: 500
测试节点: 1000接下来我们实现GCN的核心组件
python
def preprocess_adj(A):
"""
预处理邻接矩阵,计算 D^(-1/2) * (A + I) * D^(-1/2)
参数:
A: 邻接矩阵 (num_nodes, num_nodes)
返回:
归一化后的邻接矩阵
"""
# 添加自环: A_hat = A + I
I = torch.eye(A.shape[0])
A_hat = A + I
# 计算度矩阵 D
D = torch.diag(A_hat.sum(dim=1))
# 计算 D^(-1/2)
D_inv_sqrt = torch.diag(torch.pow(D.diag(), -0.5))
# 将无穷大值替换为0(处理度为0的节点)
D_inv_sqrt[torch.isinf(D_inv_sqrt)] = 0
# 计算归一化的邻接矩阵: D^(-1/2) * A_hat * D^(-1/2)
A_normalized = torch.mm(torch.mm(D_inv_sqrt, A_hat), D_inv_sqrt)
return A_normalized
# 预处理我们的邻接矩阵
A_norm = preprocess_adj(A)
print(f"原始邻接矩阵形状: {A.shape}")
print(f"归一化邻接矩阵形状: {A_norm.shape}")
print(f"归一化后矩阵的值范围: [{A_norm.min():.4f}, {A_norm.max():.4f}]")原始邻接矩阵形状: torch.Size([2708, 2708])
归一化邻接矩阵形状: torch.Size([2708, 2708])
归一化后矩阵的值范围: [0.0000, 0.5000]实现GCN层
python
class GCNLayer(nn.Module):
"""
单个GCN层的实现
公式: H^(k) = σ(A_norm * H^(k-1) * W^(k))
"""
def __init__(self, in_features, out_features, bias=True):
super(GCNLayer, self).__init__()
self.in_features = in_features
self.out_features = out_features
# 可训练的权重矩阵 W
self.weight = nn.Parameter(torch.FloatTensor(in_features, out_features))
# 偏置项(可选)
if bias:
self.bias = nn.Parameter(torch.FloatTensor(out_features))
else:
self.register_parameter('bias', None)
# 初始化参数
self.reset_parameters()
def reset_parameters(self):
"""初始化权重和偏置"""
nn.init.xavier_uniform_(self.weight)
if self.bias is not None:
nn.init.zeros_(self.bias)
def forward(self, input_features, adj_matrix):
"""
前向传播
参数:
input_features: 输入特征矩阵 H^(k-1) (num_nodes, in_features)
adj_matrix: 归一化的邻接矩阵 A_norm (num_nodes, num_nodes)
返回:
output: 输出特征矩阵 H^(k) (num_nodes, out_features)
"""
# 步骤1: H^(k-1) * W^(k) - 线性变换
support = torch.mm(input_features, self.weight)
# 步骤2: A_norm * (H^(k-1) * W^(k)) - 图卷积
output = torch.mm(adj_matrix, support)
# 步骤3: 添加偏置
if self.bias is not None:
output = output + self.bias
return output
def __repr__(self):
return f'{self.__class__.__name__} ({self.in_features} -> {self.out_features})'
# 测试GCN层
test_layer = GCNLayer(X.shape[1], 16)
test_output = test_layer(X, A_norm)
print(f"测试GCN层:")
print(f"输入形状: {X.shape}")
print(f"输出形状: {test_output.shape}")
print(f"层参数: {test_layer}")测试GCN层:
输入形状: torch.Size([2708, 1433])
输出形状: torch.Size([2708, 16])
层参数: GCNLayer (1433 -> 16)构建完整的GCN模型
python
class GCN(nn.Module):
"""
完整的图卷积网络模型
包含两个GCN层和dropout正则化
"""
def __init__(self, input_dim, hidden_dim, output_dim, dropout=0.5):
super(GCN, self).__init__()
# 第一个GCN层
self.gc1 = GCNLayer(input_dim, hidden_dim)
# 第二个GCN层
self.gc2 = GCNLayer(hidden_dim, output_dim)
# Dropout层用于正则化
self.dropout = nn.Dropout(dropout)
def forward(self, x, adj):
"""
前向传播
参数:
x: 节点特征矩阵 (num_nodes, input_dim)
adj: 归一化的邻接矩阵 (num_nodes, num_nodes)
返回:
输出: 节点的类别预测 (num_nodes, output_dim)
"""
# 第一层: GCN + ReLU + Dropout
x = self.gc1(x, adj)
x = F.relu(x)
x = self.dropout(x)
# 第二层: GCN(输出层,不需要激活函数)
x = self.gc2(x, adj)
return x
def get_embeddings(self, x, adj):
"""
获取节点的嵌入表示(第一层的输出)
用于可视化
"""
x = self.gc1(x, adj)
x = F.relu(x)
return x
# 创建模型
model = GCN(input_dim=X.shape[1],
hidden_dim=16,
output_dim=len(torch.unique(y)),
dropout=0.5)
print("GCN模型结构:")
print(model)
print(f"\n模型参数数量: {sum(p.numel() for p in model.parameters() if p.requires_grad)}")GCN模型结构:
GCN(
(gc1): GCNLayer (1433 -> 16)
(gc2): GCNLayer (16 -> 7)
(dropout): Dropout(p=0.5, inplace=False)
)
模型参数数量: 23063训练模型
python
def train_gcn(model, X, A_norm, y, train_mask, val_mask, epochs=200, lr=0.01, weight_decay=5e-4):
"""
训练GCN模型
"""
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=weight_decay)
criterion = nn.CrossEntropyLoss()
train_losses = []
val_losses = []
train_accuracies = []
val_accuracies = []
model.train()
for epoch in range(epochs):
# 前向传播
optimizer.zero_grad()
outputs = model(X, A_norm)
# 计算训练损失(只在训练节点上)
train_loss = criterion(outputs[train_mask], y[train_mask])
# 反向传播
train_loss.backward()
optimizer.step()
# 计算验证损失和准确率
model.eval()
with torch.no_grad():
val_outputs = model(X, A_norm)
val_loss = criterion(val_outputs[val_mask], y[val_mask])
# 计算准确率
train_pred = outputs[train_mask].argmax(dim=1)
train_acc = (train_pred == y[train_mask]).float().mean()
val_pred = val_outputs[val_mask].argmax(dim=1)
val_acc = (val_pred == y[val_mask]).float().mean()
model.train()
# 记录指标
train_losses.append(train_loss.item())
val_losses.append(val_loss.item())
train_accuracies.append(train_acc.item())
val_accuracies.append(val_acc.item())
# 打印进度
if (epoch + 1) % 50 == 0:
print(f'Epoch {epoch+1:3d}, Train Loss: {train_loss:.4f}, Val Loss: {val_loss:.4f}, '
f'Train Acc: {train_acc:.4f}, Val Acc: {val_acc:.4f}')
return train_losses, val_losses, train_accuracies, val_accuracies
# 训练模型
print("开始训练GCN模型...")
train_losses, val_losses, train_accs, val_accs = train_gcn(
model, X, A_norm, y, train_mask, val_mask, epochs=1000
)开始训练GCN模型...
Epoch 50, Train Loss: 1.1668, Val Loss: 1.4901, Train Acc: 0.8357, Val Acc: 0.7460
Epoch 100, Train Loss: 0.6426, Val Loss: 1.0536, Train Acc: 0.9571, Val Acc: 0.7880
Epoch 150, Train Loss: 0.4192, Val Loss: 0.9040, Train Acc: 0.9643, Val Acc: 0.7820
Epoch 200, Train Loss: 0.3467, Val Loss: 0.8285, Train Acc: 0.9857, Val Acc: 0.7860
Epoch 250, Train Loss: 0.2661, Val Loss: 0.7869, Train Acc: 0.9929, Val Acc: 0.7940
Epoch 300, Train Loss: 0.2703, Val Loss: 0.7626, Train Acc: 0.9714, Val Acc: 0.7900
Epoch 350, Train Loss: 0.2115, Val Loss: 0.7525, Train Acc: 0.9929, Val Acc: 0.7900
Epoch 400, Train Loss: 0.2284, Val Loss: 0.7356, Train Acc: 0.9857, Val Acc: 0.7900
Epoch 450, Train Loss: 0.2013, Val Loss: 0.7236, Train Acc: 0.9929, Val Acc: 0.7940
Epoch 500, Train Loss: 0.2387, Val Loss: 0.7241, Train Acc: 0.9714, Val Acc: 0.7940
Epoch 550, Train Loss: 0.2096, Val Loss: 0.7274, Train Acc: 0.9929, Val Acc: 0.7900
Epoch 600, Train Loss: 0.2029, Val Loss: 0.7171, Train Acc: 0.9929, Val Acc: 0.7920
Epoch 650, Train Loss: 0.1772, Val Loss: 0.7193, Train Acc: 1.0000, Val Acc: 0.7940
Epoch 700, Train Loss: 0.2201, Val Loss: 0.7237, Train Acc: 0.9786, Val Acc: 0.7860
Epoch 750, Train Loss: 0.1839, Val Loss: 0.7144, Train Acc: 1.0000, Val Acc: 0.7900
Epoch 800, Train Loss: 0.1967, Val Loss: 0.7281, Train Acc: 0.9857, Val Acc: 0.7840
Epoch 850, Train Loss: 0.1943, Val Loss: 0.7106, Train Acc: 0.9929, Val Acc: 0.7920
Epoch 900, Train Loss: 0.2040, Val Loss: 0.6959, Train Acc: 0.9786, Val Acc: 0.7960
Epoch 950, Train Loss: 0.1866, Val Loss: 0.7045, Train Acc: 0.9929, Val Acc: 0.7940
Epoch 1000, Train Loss: 0.1846, Val Loss: 0.7191, Train Acc: 0.9929, Val Acc: 0.7860评估模型性能
python
def evaluate_model(model, X, A_norm, y, test_mask):
"""
在测试集上评估模型
"""
model.eval()
with torch.no_grad():
outputs = model(X, A_norm)
test_pred = outputs[test_mask].argmax(dim=1)
test_acc = (test_pred == y[test_mask]).float().mean()
# 计算各类别的预测情况
pred_all = outputs.argmax(dim=1)
return test_acc.item(), pred_all, test_pred
# 评估模型
test_accuracy, predictions, test_predictions = evaluate_model(model, X, A_norm, y, test_mask)
print(f"\n测试集准确率: {test_accuracy:.4f}")
# 详细的分类结果
from sklearn.metrics import classification_report
test_true = y[test_mask].numpy()
test_pred = test_predictions.numpy()
print("\n测试集分类报告:")
print(classification_report(test_true, test_pred, target_names=[f'Class {i}' for i in range(len(torch.unique(y)))]))测试集准确率: 0.8070
测试集分类报告:
precision recall f1-score support
Class 0 0.64 0.81 0.71 130
Class 1 0.76 0.86 0.81 91
Class 2 0.87 0.86 0.86 144
Class 3 0.91 0.78 0.84 319
Class 4 0.80 0.86 0.83 149
Class 5 0.87 0.72 0.79 103
Class 6 0.70 0.78 0.74 64
accuracy 0.81 1000
macro avg 0.79 0.81 0.80 1000
weighted avg 0.82 0.81 0.81 1000可视化结果
python
# 绘制训练过程
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(12, 8))
# 损失曲线
ax1.plot(train_losses, label='Train Loss', color='blue')
ax1.plot(val_losses, label='Validation Loss', color='red')
ax1.set_title('Training and Validation Loss')
ax1.set_xlabel('Epoch')
ax1.set_ylabel('Loss')
ax1.legend()
ax1.grid(True)
# 准确率曲线
ax2.plot(train_accs, label='Train Accuracy', color='blue')
ax2.plot(val_accs, label='Validation Accuracy', color='red')
ax2.set_title('Training and Validation Accuracy')
ax2.set_xlabel('Epoch')
ax2.set_ylabel('Accuracy')
ax2.legend()
ax2.grid(True)
# 最终损失对比
categories = ['Train', 'Validation']
final_losses = [train_losses[-1], val_losses[-1]]
ax3.bar(categories, final_losses, color=['blue', 'red'], alpha=0.7)
ax3.set_title('The Final Loss Comparison')
ax3.set_ylabel('Loss')
# 最终准确率对比
final_accs = [train_accs[-1], val_accs[-1]]
ax4.bar(categories, final_accs, color=['blue', 'red'], alpha=0.7)
ax4.set_title('The Final Accuracy Comparison')
ax4.set_ylabel('Accuracy')
plt.tight_layout()
plt.show()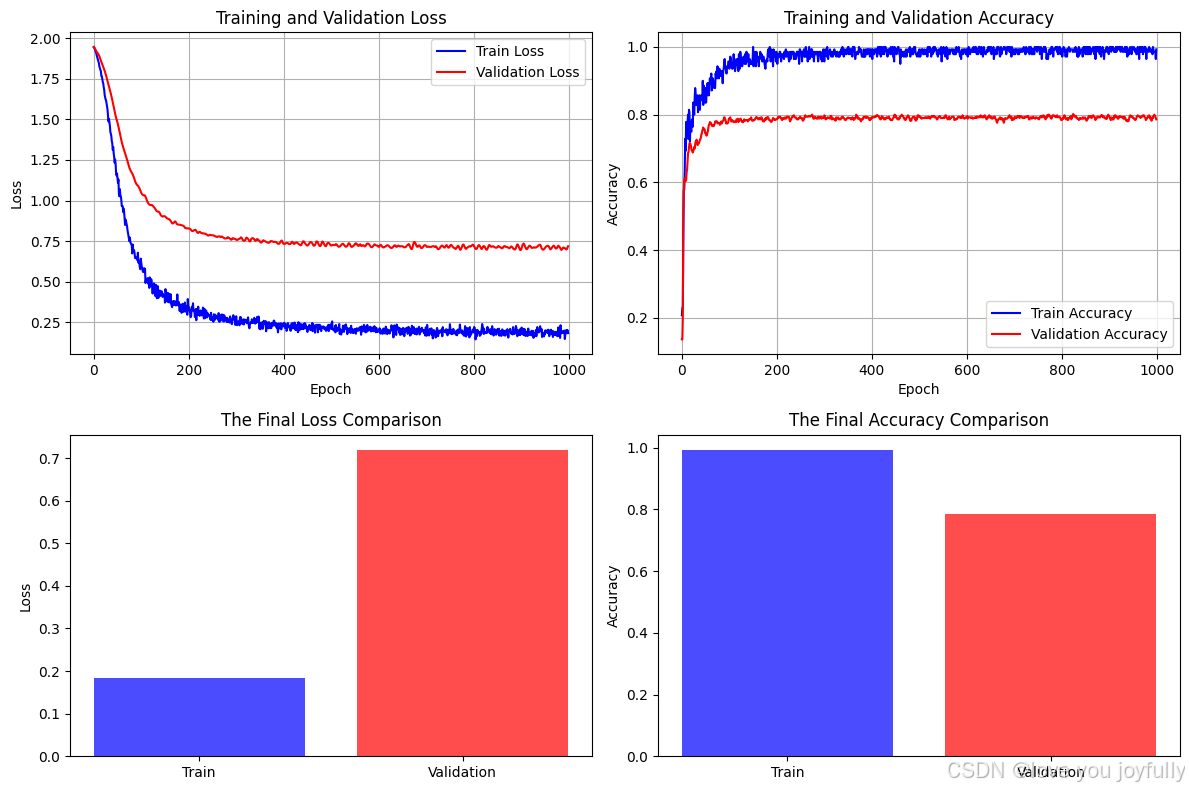
节点嵌入可视化
python
# 获取节点嵌入并进行t-SNE降维可视化
model.eval()
with torch.no_grad():
embeddings = model.get_embeddings(X, A_norm).numpy()
# 使用t-SNE进行降维
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
embeddings_2d = tsne.fit_transform(embeddings)
# 为7个类别定义颜色
colors = ['red', 'blue', 'green', 'orange', 'purple', 'brown', 'pink']
# 可视化
plt.figure(figsize=(15, 5))
# 原始标签的可视化
plt.subplot(1, 3, 1)
for i in range(len(torch.unique(y))):
mask = (y == i).numpy()
plt.scatter(embeddings_2d[mask, 0], embeddings_2d[mask, 1],
c=colors[i], label=f'Class {i}', alpha=0.7, s=30)
plt.title('Node Embedding Visualization (True Labels)')
plt.xlabel('t-SNE 1')
plt.ylabel('t-SNE 2')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
# 预测标签的可视化
plt.subplot(1, 3, 2)
pred_labels = predictions.numpy()
for i in range(len(torch.unique(y))):
mask = (pred_labels == i)
plt.scatter(embeddings_2d[mask, 0], embeddings_2d[mask, 1],
c=colors[i], label=f'Predicted Class {i}', alpha=0.7, s=30)
plt.title('Node Embedding Visualization (Predicted Labels)')
plt.xlabel('t-SNE 1')
plt.ylabel('t-SNE 2')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
# 训练/测试节点分布可视化
plt.subplot(1, 3, 3)
# 绘制测试节点(通常是我们关注的重点)
test_mask_np = test_mask.numpy()
train_mask_np = train_mask.numpy()
# 用不同形状区分训练和测试节点
plt.scatter(embeddings_2d[train_mask_np, 0], embeddings_2d[train_mask_np, 1],
c='lightgray', alpha=0.5, s=20, marker='o', label='Train Nodes')
plt.scatter(embeddings_2d[test_mask_np, 0], embeddings_2d[test_mask_np, 1],
c='black', alpha=0.8, s=30, marker='s', label='Test Nodes')
plt.title('Train/Test Node Distribution')
plt.xlabel('t-SNE 1')
plt.ylabel('t-SNE 2')
plt.legend()
plt.tight_layout()
plt.show()
# 计算并显示分类准确率
test_accuracy = (pred_labels[test_mask.numpy()] == y[test_mask.numpy()]).float().mean()
print(f"Test Accuracy: {test_accuracy:.4f}")
# 显示各类别的预测准确率
print("\nAccuracy per class:")
for i in range(len(torch.unique(y))):
class_mask = (y == i) & test_mask
if class_mask.sum() > 0:
class_acc = (pred_labels[class_mask.numpy()] == y[class_mask.numpy()]).float().mean()
print(f"Class {i}: {class_acc:.4f}")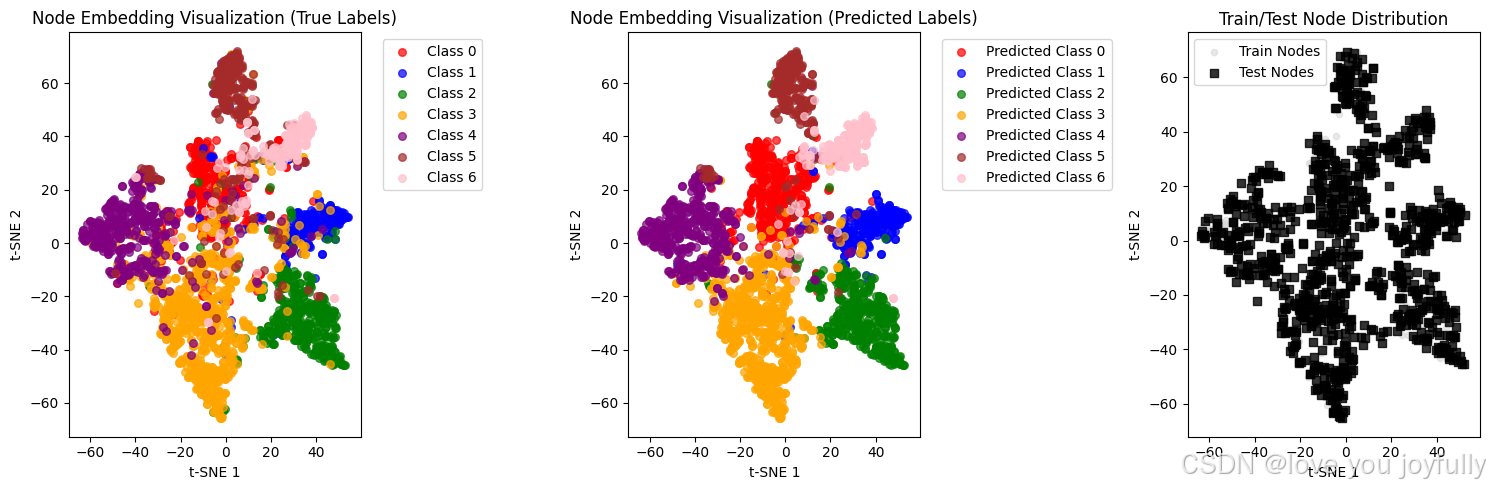
Test Accuracy: 0.8070
Accuracy per class:
Class 0: 0.8077
Class 1: 0.8571
Class 2: 0.8611
Class 3: 0.7774
Class 4: 0.8591
Class 5: 0.7184
Class 6: 0.7812(2) GraphSAGE (Graph SAmple and aggreGatE)
GraphSAGE 对 GCN 进行了扩展,核心改进在于将聚合函数变成了一个可学习、可选择的通用模块。
其流程分为两步:
-
聚合 (AGGREGATE) :
av(k)=AGGREGATOR({hu(k−1),∀u∈N(v)})a_v^{(k)} = \text{AGGREGATOR} \left( \{ h_u^{(k-1)}, \forall u \in \mathcal{N}(v) \} \right)av(k)=AGGREGATOR({hu(k−1),∀u∈N(v)})GraphSAGE 提出了多种聚合器:
- Mean Aggregator : av(k)=1∣N(v)∣∑u∈N(v)hu(k−1)a_v^{(k)} = \frac{1}{|\mathcal{N}(v)|} \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)}av(k)=∣N(v)∣1∑u∈N(v)hu(k−1) (近似 GCN)
- LSTM Aggregator: 将邻居节点随机打乱顺序后,输入到一个 LSTM 中。
- Pooling Aggregator : av(k)=max({σ(Wpoolhu(k−1)+b),∀u∈N(v)})a_v^{(k)} = \max \left( \{ \sigma(W_{\text{pool}} h_u^{(k-1)} + b), \forall u \in \mathcal{N}(v) \} \right)av(k)=max({σ(Wpoolhu(k−1)+b),∀u∈N(v)}) (对每个邻居特征做一次非线性变换后取最大值)
-
更新 (UPDATE) :
将上一步聚合的邻居信息 av(k)a_v^{(k)}av(k) 与节点自身上一层的表示 hv(k−1)h_v^{(k-1)}hv(k−1) **拼接(Concat)**起来,然后通过一个全连接层。
hv(k)=σ(W(k)⋅CONCAT(hv(k−1),av(k)))h_v^{(k)} = \sigma \left( W^{(k)} \cdot \text{CONCAT}(h_v^{(k-1)}, a_v^{(k)}) \right)hv(k)=σ(W(k)⋅CONCAT(hv(k−1),av(k)))
GraphSAGE 的一个重要贡献是其**归纳学习(Inductive Learning)**能力。由于其聚合器是通用的,它可以为在训练期间从未见过的全新节点生成嵌入。
(3) 图注意力网络 (GAT - Graph Attention Network)
GCN 和 GraphSAGE 在聚合邻居信息时,对所有邻居"一视同仁"(或使用固定的权重)。但直觉上,不同的邻居节点对当前节点的重要性应该是不同的。GAT 引入了**注意力机制(Attention Mechanism)**来解决这个问题。
GAT 的核心思想是:在聚合邻居信息时,为每个邻居动态地计算一个注意力权重。
对于节点 iii 和其邻居 jjj,注意力权重 αij\alpha_{ij}αij 的计算过程如下:
- 对节点特征进行线性变换:WhiW h_iWhi 和 WhjW h_jWhj。
- 计算一个注意力系数 eije_{ij}eij,表示节点 jjj 的信息对节点 iii 的重要性:
eij=a(Whi,Whj)e_{ij} = a(W h_i, W h_j)eij=a(Whi,Whj)
其中 aaa 是一个可学习的注意力函数,通常是一个单层前馈网络。 - 使用
softmax函数对所有邻居的注意力系数进行归一化,得到最终的注意力权重:
αij=softmaxj(eij)=exp(eij)∑k∈N(i)exp(eik)\alpha_{ij} = \text{softmax}j(e{ij}) = \frac{\exp(e_{ij})}{\sum_{k \in \mathcal{N}(i)} \exp(e_{ik})}αij=softmaxj(eij)=∑k∈N(i)exp(eik)exp(eij) - 使用注意力权重对邻居节点的特征进行加权求和,完成聚合:
hi′=σ(∑j∈N(i)αijWhj)h_i' = \sigma \left( \sum_{j \in \mathcal{N}(i)} \alpha_{ij} W h_j \right)hi′=σ(∑j∈N(i)αijWhj)
GAT 还引入了多头注意力(Multi-head Attention),并行计算多组独立的注意力权重,然后将结果拼接或平均,使模型学习过程更稳定,表达能力更强。
GNN 凭借其强大的图数据建模能力,已在众多领域展现出巨大潜力:
- 推荐系统:构建"用户-物品"二部图,预测用户可能喜欢的物品(链接预测)。
- 药物发现与分子科学:将分子看作图,预测其化学性质或生物活性(图分类)。
- 计算机视觉:场景图生成、点云分割等。
- 自然语言处理:用于句子语法分析树、文本关系抽取等。
- 交通流量预测:将交通网络建模为图,预测未来各路段的流量。
图神经网络通过消息传递机制 ,巧妙地将节点的特征信息与其在图中的拓扑结构信息相融合,生成了富有表现力的节点嵌入。从 GCN 的简单加权平均,到 GraphSAGE 的通用聚合器,再到 GAT 的注意力机制,GNN 模型不断演进,其核心都是在探索如何更有效地聚合邻域信息。